Wie kann ich mit Python überprüfen, ob Zeitreihendaten stationär sind?

Eine Zeitreihe ist eine Reihe von Datenpunkten, die in regelmäßigen Abständen aufgezeichnet werden. Es wird verwendet, um Mustertrends, Beziehungen zwischen Variablen und Änderungen über einen definierten Zeitraum zu untersuchen. Gängige Beispiele für Zeitreihen sind Aktienkurse, Wettermuster und Wirtschaftsindikatoren.

Analysieren Sie Zeitreihendaten mithilfe statistischer und mathematischer Techniken. Der Hauptzweck von Zeitreihen besteht darin, Muster und Trends in früheren Daten zu identifizieren, um zukünftige Werte vorherzusagen.

Die Daten gelten als stationär. Wenn sie sich nicht mit der Zeit ändern, muss überprüft werden, ob die Daten stationär sind oder nicht. Es gibt verschiedene Möglichkeiten, um zu überprüfen, ob Zeitreihendaten stationär sind eins.

Augmented Dickey-Fuller (ADF)

Augmented Dickey-Fuller (ADF) ist ein statistischer Test, der das Vorhandensein der in den Zeitreihendaten verfügbaren Einheitswurzeln prüft. Die Einheitswurzel sind die Daten, die nicht stationär sind. Sie geben den statischen Test und den p-Wert als Ausgabe zurück .

Wenn der p-Wert in der Ausgabe kleiner als 0,05 ist, handelt es sich um instationäre Zeitreihendaten. Nachfolgend finden Sie ein Beispiel für stationäre ADF-Daten. Wir haben in Python eine Funktion namens adfuller(), die im Paket statsmodel verfügbar ist, um zu überprüfen, ob die Zeitreihendaten stationär sind oder nicht.

Beispiel

In diesem Beispiel ermitteln wir die ADF-Statistik und den p-Wert des Augmented Dickey Fuller mithilfe der Funktion adfuller() des statsmodel-Pakets von Python.

from statsmodels.tsa.stattools import adfuller
import pandas as pd
data = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv',parse_dates=['date'], index_col='date')
t_data = data.loc[:, 'value'].values
result = adfuller(t_data)
print("The result of adfuller function:",result)
print('ADF Statistic:', result[0])
print('p-value:', result[1])

Ausgabe

Es folgt die Ausgabe, die nach der Ausführung des obigen Programms erzeugt wird –

The result of adfuller function: (3.145185689306744, 1.0, 15, 188, {'1%': -3.465620397124192, '5%': -2.8770397560752436, '10%': -2.5750324547306476}, 549.6705685364172)
ADF Statistic: 3.145185689306744
p-value: 1.0

KPSS-Test

Ein weiterer Test zur Überprüfung auf Einheitswurzeln ist der KPSS-Test. Die Abkürzung lautet Kwiatkowski-Phillips-Schmidt-Shin. Wir haben eine Funktion namens kpss() im statsmodels-Paket zum Überprüfen von Einheitswurzeln in Zeitreihendaten.

Beispiel

Nachfolgend finden Sie ein Beispiel für die Suche nach Einheitswurzeln in Zeitreihendaten.

from statsmodels.tsa.stattools import kpss
import pandas as pd
data = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv',parse_dates=['date'], index_col='date')
t_data = data.loc[:, 'value'].values
from statsmodels.tsa.stattools import kpss
result = kpss(data)
print("The result of kpss function:",result)
print('KPSS Statistic:', result[0])
print('p-value:', result[1])

Ausgabe

Das Folgende ist das Ausgabeergebnis der Funktion kpss() im Paket statsmodels.

The result of kpss function: (2.0131256386303322, 0.01, 9, {'10%': 0.347, '5%': 0.463, '2.5%': 0.574, '1%': 0.739})
KPSS Statistic: 2.0131256386303322
p-value: 0.01

Scrollende Statistiken

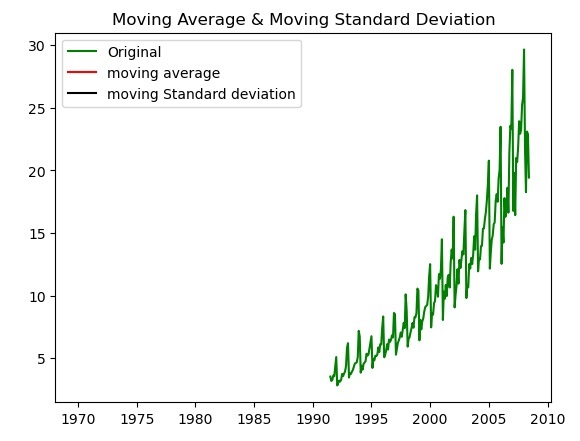
Eine andere Möglichkeit, Zeitreihendaten zu überprüfen, besteht darin, den gleitenden Durchschnitt und die gleitende Standardabweichung der gegebenen Zeitreihendaten darzustellen und zu prüfen, ob die Daten konstant bleiben. Wenn sich die Daten im Diagramm im Laufe der Zeit ändern, sind die Zeitreihendaten instationär.

Beispiel

Das Folgende ist das Beispiel für die Überprüfung der Datenvariation durch Auftragen des gleitenden Durchschnitts und der gleitenden Standardabweichung mithilfe der matplotlib-Bibliotheksfunktion plot().

import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv',parse_dates=['date'], index_col='date')
t_data = data.loc[:, 'value'].values
moving_avg = t_data.mean()
moving_std = t_data.std()
plt.plot(data, color='green', label='Original')
plt.plot(moving_avg, color='red', label='moving average')
plt.plot(moving_std, color='black', label='moving Standard deviation')
plt.legend(loc='best')
plt.title('Moving Average & Moving Standard Deviation')
plt.show()

Ausgabe

Unten sehen Sie die Ausgabe der Normalisierung von Zeitreihendaten durch Auftragen des gleitenden Durchschnitts und der gleitenden Standardabweichung.

Das obige ist der detaillierte Inhalt vonWie kann ich mit Python überprüfen, ob Zeitreihendaten stationär sind?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!