 Web-Frontend
Web-Frontend
 js-Tutorial
js-Tutorial
 JavaScript-Programm zur Überprüfung der horizontalen und vertikalen Symmetrie in binären Matrizen
JavaScript-Programm zur Überprüfung der horizontalen und vertikalen Symmetrie in binären Matrizen
JavaScript-Programm zur Überprüfung der horizontalen und vertikalen Symmetrie in binären Matrizen

Eine binäre Matrix ist ein zweidimensionales Array, das in jeder Zelle nur 1 und 0 Elemente enthält. Die horizontale Symmetrie einer Binärmatrix bedeutet, dass, wenn die erste Zeile mit der letzten Zeile übereinstimmt, die zweite Zeile mit der vorletzten Zeile übereinstimmt und so weiter. Ebenso bedeutet vertikale Symmetrie, ob die erste und letzte Spalte, die vorletzte Spalte und die vorletzte Spalte usw. gleich sind. In diesem Problem erhalten wir eine Matrix und werden feststellen, ob darin horizontale und vertikale Symmetrie vorliegt.
Eintreten
1 0 1 0 0 0 1 0 1
Ausgabe
Both, horizontal and vertical symmetry is present.
Erklärung- Die erste und letzte Reihe sind gleich, was bedeutet, dass horizontale Symmetrie vorliegt. Ebenso sind die erste und letzte Spalte identisch, was zu einer vertikalen Symmetrie führt.
Eintreten
1 0 1 0 0 0 1 1 0
Ausgabe
None of the symmetry is present.
Erklärung – Die erste Zeile ist nicht gleich der letzten Zeile und die erste Spalte ist nicht gleich der letzten Spalte.
Methode
Wir haben Beispiele gesehen, um das gegebene Problem zu verstehen. Schauen wir uns nun die Schritte zur Implementierung des Codes an -
Zuerst definieren wir eine Funktion, um die horizontale Symmetrie einer gegebenen Matrix zu überprüfen. Diese Funktion nimmt ein einzelnes Argument der gegebenen Matrix und gibt zurück, ob die aktuelle Matrix horizontal symmetrisch ist.
Wir durchlaufen die Matrix und vergleichen jede Zeile mit der Zeile auf der anderen Seite einer imaginären Linie, die durch die Mitte der Matrix verläuft und den gleichen Abstand von der aktuellen Zeile hat.
Wir werden eine Funktion definieren, um die vertikale Symmetrie einer bestimmten Matrix zu überprüfen. Diese Funktion benötigt ein Argument, die angegebene Matrix.
Wir durchlaufen die Matrix und vergleichen jede Spalte mit der Spalte auf der anderen Seite einer imaginären Linie, die durch die Mitte der Matrix verläuft und den gleichen Abstand von der aktuellen Spalte hat.
Wir rufen diese beiden Funktionen auf und drucken die Ergebnisse basierend auf den Rückgabewerten aus.
Beispiel
// function to check horizontal symmetry
function horizontalSymm(mat){
var rows = mat.length;
var cols = mat[0].length;
for(var i = 0; i< rows/2; i++){
for(var j = 0;j<cols; j++){
if(mat[i][j] != mat[rows-i-1][j]){
return false;
}
}
}
return true;
}
// function to check vertical symmetry
function verticalSymm(mat){
var rows = mat.length;
var cols = mat[0].length;
for(var i = 0; i< cols/2; i++){
for(var j = 0;j<rows; j++){
if(mat[j][i] != mat[j][cols-i-1]){
return false;
}
}
}
return true;
}
// function to check the symmetry of the given matrix
function check(mat){
var horSymm = horizontalSymm(mat);
var varSymm = verticalSymm(mat);
if(horSymm && varSymm){
console.log("Both, horizontal and vertical symmetries are present in the given matrix");
}
else if(horSymm){
console.log("The given binary matrix is only horizontally symmetric");
}
else if(varSymm){
console.log("The given binary matrix is only vertically symmetric");
}
else{
console.log("The given binary matrix is neither horizontally symmetric nor vertically symmetric");
}
}
// defining the given matrix
var mat = [[1, 0, 1], [0, 0, 0], [1, 0, 1]];
console.log("The given matrix is: ")
console.log(mat);
check(mat);
// defining the given matrix
var mat = [[1, 0, 1], [0, 0, 0], [1, 1, 0]];
console.log("The given matrix is: ")
console.log(mat);
check(mat);
Ausgabe
The given matrix is: [ [ 1, 0, 1 ], [ 0, 0, 0 ], [ 1, 0, 1 ] ] Both, horizontal and vertical symmetries are present in the given matrix The given matrix is: [ [ 1, 0, 1 ], [ 0, 0, 0 ], [ 1, 1, 0 ] ] The given binary matrix is neither horizontally symmetric nor vertically symmetric
Zeitliche und räumliche Komplexität
Die zeitliche Komplexität des obigen Codes beträgt O(N*M), wobei N die Anzahl der Zeilen der gegebenen Matrix und M die Anzahl der Spalten der gegebenen Matrix ist. Wir werden die gesamte Matrix zweimal durchlaufen, einmal für horizontale Symmetrie und einmal für vertikale Symmetrie.
Die Speicherplatzkomplexität des obigen Codes beträgt O(1), da wir keinen zusätzlichen Speicherplatz verwenden.
Fazit
In diesem Tutorial haben wir ein JavaScript-Programm implementiert, um herauszufinden, ob eine bestimmte Matrix horizontal oder vertikal symmetrisch ist. Die horizontale Symmetrie einer binären Matrix bedeutet, dass, wenn die erste Zeile mit der letzten Zeile identisch ist, die zweite Zeile mit der vorletzten Zeile identisch ist und so weiter. Ebenso bedeutet vertikale Symmetrie, ob die erste und letzte Spalte, die vorletzte Spalte und die vorletzte Spalte usw. gleich sind. Wir haben ein Programm mit der Zeitkomplexität O(N*M) und der Raumkomplexität O(1) implementiert.
Das obige ist der detaillierte Inhalt vonJavaScript-Programm zur Überprüfung der horizontalen und vertikalen Symmetrie in binären Matrizen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Ersetzen Sie Stringzeichen in JavaScript
Mar 11, 2025 am 12:07 AM
Ersetzen Sie Stringzeichen in JavaScript
Mar 11, 2025 am 12:07 AM
Detaillierte Erläuterung der Methode für JavaScript -Zeichenfolge und FAQ In diesem Artikel werden zwei Möglichkeiten untersucht, wie String -Zeichen in JavaScript ersetzt werden: Interner JavaScript -Code und interne HTML für Webseiten. Ersetzen Sie die Zeichenfolge im JavaScript -Code Die direkteste Möglichkeit ist die Verwendung der Ersatz () -Methode: str = str.replace ("find", "ersetzen"); Diese Methode ersetzt nur die erste Übereinstimmung. Um alle Übereinstimmungen zu ersetzen, verwenden Sie einen regulären Ausdruck und fügen Sie das globale Flag G hinzu:: STR = Str.Replace (/fi
 Benutzerdefinierte Google -Search -API -Setup -Tutorial
Mar 04, 2025 am 01:06 AM
Benutzerdefinierte Google -Search -API -Setup -Tutorial
Mar 04, 2025 am 01:06 AM
Dieses Tutorial zeigt Ihnen, wie Sie eine benutzerdefinierte Google -Such -API in Ihr Blog oder Ihre Website integrieren und ein raffinierteres Sucherlebnis bieten als Standard -WordPress -Themen -Suchfunktionen. Es ist überraschend einfach! Sie können die Suche auf y beschränken
 10 JQuery Syntax Highlighters
Mar 02, 2025 am 12:32 AM
10 JQuery Syntax Highlighters
Mar 02, 2025 am 12:32 AM
Verbessern Sie Ihre Codepräsentation: 10 Syntax -Hochlichter für Entwickler Das Teilen von Code -Snippets auf Ihrer Website oder Ihrem Blog ist eine gängige Praxis für Entwickler. Die Auswahl des richtigen Syntax -Highlighter kann die Lesbarkeit und die visuelle Anziehungskraft erheblich verbessern. T
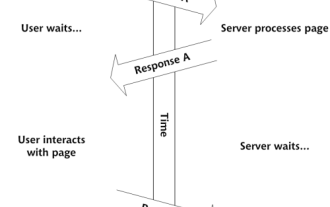 Erstellen Sie Ihre eigenen AJAX -Webanwendungen
Mar 09, 2025 am 12:11 AM
Erstellen Sie Ihre eigenen AJAX -Webanwendungen
Mar 09, 2025 am 12:11 AM
Hier sind Sie also bereit, alles über dieses Ding namens Ajax zu lernen. Aber was genau ist das? Der Begriff AJAX bezieht sich auf eine lose Gruppierung von Technologien, mit denen dynamische, interaktive Webinhalte erstellt werden. Der Begriff Ajax, ursprünglich von Jesse J geprägt
 Beispielfarben JSON -Datei
Mar 03, 2025 am 12:35 AM
Beispielfarben JSON -Datei
Mar 03, 2025 am 12:35 AM
Diese Artikelserie wurde Mitte 2017 mit aktuellen Informationen und neuen Beispielen umgeschrieben. In diesem JSON -Beispiel werden wir uns ansehen, wie wir einfache Werte in einer Datei mit JSON -Format speichern können. Mit der Notation des Schlüsselwertpaares können wir jede Art speichern
 8 atemberaubende JQuery -Seiten -Layout -Plugins
Mar 06, 2025 am 12:48 AM
8 atemberaubende JQuery -Seiten -Layout -Plugins
Mar 06, 2025 am 12:48 AM
Nutzen Sie JQuery für mühelose Webseiten -Layouts: 8 Essential Plugins JQuery vereinfacht das Webseitenlayout erheblich. In diesem Artikel werden acht leistungsstarke JQuery -Plugins hervorgehoben, die den Prozess optimieren, insbesondere nützlich für die manuelle Website -Erstellung
 10 JavaScript & JQuery MVC -Tutorials
Mar 02, 2025 am 01:16 AM
10 JavaScript & JQuery MVC -Tutorials
Mar 02, 2025 am 01:16 AM
Dieser Artikel enthält eine kuratierte Auswahl von über 10 Tutorials zu JavaScript- und JQuery Model-View-Controller-Frameworks (MVC). Diese Tutorials decken eine Reihe von Themen von Foundatio ab
 Was ist ' this ' in JavaScript?
Mar 04, 2025 am 01:15 AM
Was ist ' this ' in JavaScript?
Mar 04, 2025 am 01:15 AM
Kernpunkte Dies in JavaScript bezieht sich normalerweise auf ein Objekt, das die Methode "besitzt", aber es hängt davon ab, wie die Funktion aufgerufen wird. Wenn es kein aktuelles Objekt gibt, bezieht sich dies auf das globale Objekt. In einem Webbrowser wird es durch Fenster dargestellt. Wenn Sie eine Funktion aufrufen, wird das globale Objekt beibehalten. Sie können den Kontext mithilfe von Methoden wie CALL (), Apply () und Bind () ändern. Diese Methoden rufen die Funktion mit dem angegebenen Wert und den Parametern auf. JavaScript ist eine hervorragende Programmiersprache. Vor ein paar Jahren war dieser Satz





