Einführung
Im Bereich Informatik und Programmierung ist das Verständnis der Effizienz von Algorithmen von entscheidender Bedeutung, da es dabei hilft, Software zu erstellen, die sowohl optimiert als auch schnell funktioniert. Zeitkomplexität ist in diesem Zusammenhang ein wichtiges Konzept, da sie misst, wie sich die Laufzeit eines Algorithmus mit zunehmender Eingabegröße ändert. Die häufig verwendete Zeitkomplexitätsklasse O(n) stellt eine lineare Beziehung zwischen Eingabegröße und Ausführungszeit dar.
Definition
Algorithmuskomplexität in der Informatik ist die Bewertung der erforderlichen Ressourcen, wie z. B. Zeit- und Raumnutzung, basierend auf der Eingabegröße eines Algorithmus. Darüber hinaus unterstützt es unser Verständnis darüber, wie schnell ein Algorithmus arbeitet, wenn seine Eingabegröße berücksichtigt wird. Die Hauptnotation zur Beschreibung der Komplexität eines Algorithmus ist die Big-O-Notation (O(n)).
Grammatik
for i in range(n):
# do something
Nach dem Login kopieren
Eine „for“-Schleife, die einen bestimmten Satz von Anweisungen basierend auf einem Bereich von 0 bis „n-1“ ausführt und bei jeder Iteration eine Operation oder einen Satz von Operationen ausführt. wobei „n“ die Anzahl der Iterationen darstellt.
Unter O(n)-Zeitkomplexität erhöht sich die Ausführungszeit proportional, wenn die Eingabegröße „n“ zunimmt. Mit zunehmendem „n“ erhöhen sich proportional die Anzahl der Schleifendurchläufe und die für den Abschluss der Schleife erforderliche Zeit. Die lineare Zeitkomplexität weist einen direkten proportionalen Zusammenhang zwischen Eingabegröße und Ausführungszeit auf.
Jede Aufgabe oder Aufgabenfolge kann unabhängig von der Eingabegröße „n“ in einer Schleife ausgeführt werden. Der Hauptaspekt, der hier zu beachten ist, ist, dass die Schleife „n“ Iterationen ausführt, was zu einer linearen Zeitkomplexität führt.
Algorithmus
Schritt 1: Initialisieren Sie eine variable Summe auf 0
Schritt 2: Durchlaufen Sie jedes Element in der bereitgestellten Liste
Schritt 3: Füge das Element zum aktuellen Summenwert zusammen.
Schritt 4: Die Summe sollte nach Ende der Schleife zurückgegeben werden.
Schritt 5: Ende
Methode
Methode 1: Zeit versus Eingabegröße grafisch darstellen
Beispiel
import time
import matplotlib.pyplot as plt
def algo_time(n):
sum = 0
for i in range(n):
sum += i
return sum
input_sizes = []
execution_times = []
for i in range(1000, 11000, 1000):
start_time = time.time()
algo_time(i)
end_time = time.time()
input_sizes.append(i)
execution_times.append(end_time - start_time)
plt.plot(input_sizes, execution_times)
plt.xlabel('Input Size')
plt.ylabel('Execution Time (s)')
plt.show()
Nach dem Login kopieren
Ausgabe
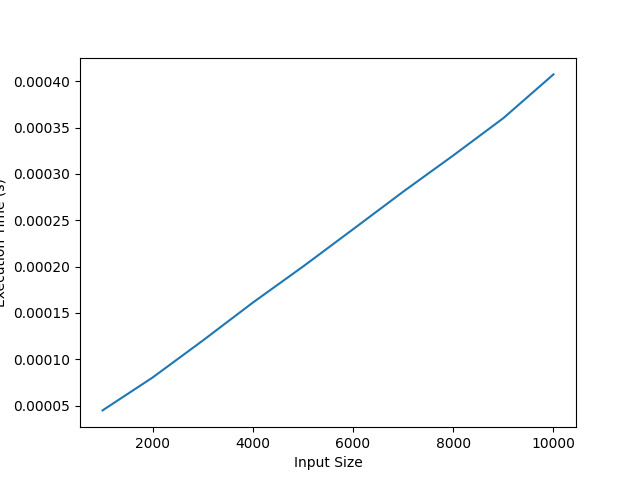
Dieser Code wird verwendet, um die Laufzeit des „algo_time()“-Algorithmus bei verschiedenen Eingabegrößen zu messen. In diesen Listen speichern wir die Eingabegrößen, die wir testen möchten, und die entsprechenden Ausführungszeiten.
Verwenden Sie eine „for“-Schleife, um über einen Bereich von Eingabegrößen zu iterieren. In diesem Fall läuft die Schleife von 1000 bis näher an 11000 und erhöht sich jedes Mal um 1000. Zur weiteren Veranschaulichung planen wir, den Algorithmus zu evaluieren, indem wir den Wert von „n“ in Schritten von 1000 von 1000 auf 10000 variieren.
Innerhalb der Schleife messen wir die Ausführungszeit der Funktion „algo_time()“ für jede Eingabegröße. Um mit der Zeiterfassung zu beginnen, verwenden wir „time.time()“, bevor wir die Funktion aufrufen, und stoppen sie, sobald die Funktion ihre Ausführung beendet hat. Anschließend speichern wir die Dauer in einer Variablen namens „execution_time“.
Wir fügen jeden Eingabewert einer bestimmten Eingabegröße ('n') und die entsprechende Ausführungszeit zu ihren jeweiligen Listen ('input_sizes' und 'execution_times') hinzu.
Nach Abschluss der Schleife verfügen wir über die Daten, die wir zum Generieren des Diagramms benötigen. „plt.plot(input_sizes, execution_times)“ generiert anhand der von uns gesammelten Daten ein einfaches Liniendiagramm. Die x-Achse zeigt „input_sizes“-Werte, die verschiedene Eingabegrößen darstellen.
'plt.xlabel()' und 'plt.ylabel()' werden schließlich verwendet, um die Bedeutung der jeweiligen Koordinatenachsen zu markieren, und der Aufruf der Funktion 'plt.show()' ermöglicht uns die Darstellung des Diagramms.
Durch die Ausführung dieses Codes können wir die Zunahme der Ausführungszeit mit zunehmender Eingabegröße ('n') visualisieren, indem wir ein Diagramm zeichnen. Unter der Annahme, dass die Zeitkomplexität des Algorithmus O(n) beträgt, können wir annähernd annehmen, dass beim Zeichnen des Diagramms eine nahezu geradlinige Korrelation zwischen der Eingabegröße und der Ausführungszeit besteht.
Methode 2: Die Beziehung zwischen Zeichenvorgang und Eingabegröße
Beispiel
import matplotlib.pyplot as plt
def algo_ops(n):
ops = 0
sum = 0
for i in range(n):
sum += i
ops += 1
ops += 1 # for the return statement
return ops
input_sizes = []
operations = []
for i in range(1000, 11000, 1000):
input_sizes.append(i)
operations.append(algo_ops(i))
plt.plot(input_sizes, operations)
plt.xlabel
plt.xlabel('Input Size')
plt.ylabel('Number of Operations')
plt.show()
Nach dem Login kopieren
Ausgabe
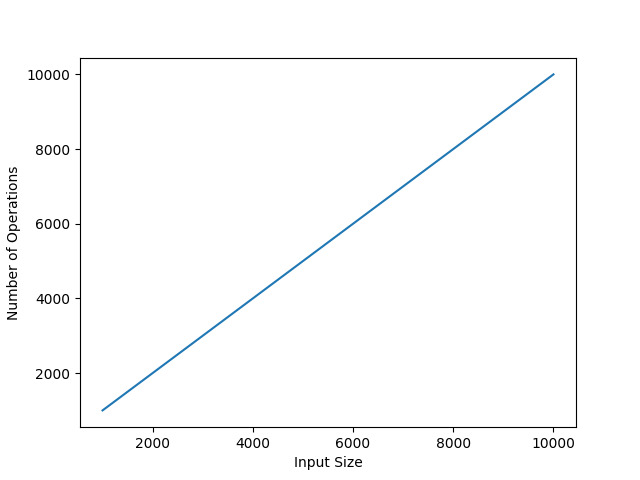
Dieser Code dient dazu, die Anzahl der vom Algorithmus „algo_ops()“ unter verschiedenen Eingabegrößen durchgeführten Operationen zu analysieren. Mithilfe der Funktion „algo_ops()“ können Sie die Summe aller Werte im Bereich von Null bis zum angegebenen Eingabeparameter „n“ berechnen und gleichzeitig jeden während jeder Berechnung durchgeführten Vorgang verfolgen und aufzeichnen.
Wir importieren zunächst das Modul „matplotlib.pyplot“, mit dem wir Visualisierungen wie Diagramme erstellen können.
Als nächstes definieren wir die Funktion algo_ops(), die eine Eingabenummer „n“ akzeptiert. Innerhalb der Funktion initialisieren wir zwei Variablen: „ops“, um die Anzahl der Operationen zu zählen, und „sum“, um die kumulative Summe der Zahlen zu speichern.
Diese Arrays speichern die Dimensionen, die wir überprüfen möchten, und die entsprechende Ausführungsdauer.
Eine Möglichkeit, iterative Schleifen zu nutzen, besteht darin, mehrere Eingabeskalen zu durchlaufen. In diesem Fall liegt der Schleifenausführungsbereich zwischen 1000 und 10000 (außer 11000). Das bedeutet, dass wir die Technik mit der Variablen „n“ zwischen 1000 und 10000 in 100er-Schritten auswerten.
In der Schleife berechnen wir die Leistung des Prozesses „algo_time()“ für alle Eingabegrößen. Wir verwenden „time.time()“, um vor dem Aufruf der Prozedur eine Stoppuhr zu starten und sie direkt zu beenden, nachdem die Ausführung der Unterroutine abgeschlossen ist. Als nächstes speichern wir das Zeitintervall in einer Variablen namens „execution_period“.
Für jede Eingabegröße fügen wir den Wert der Eingabe ('n') in eine Liste mit dem Namen 'input_sizes' ein. Zusätzlich hängen wir die entsprechenden Verarbeitungszeiten in der Sammlung „execution_times“ an.
Nachdem die Schleife abgeschlossen ist, haben wir die grundlegenden Daten gesammelt, die für die Erstellung des Diagramms erforderlich sind. Die Anweisung „plt.plot(input_sizes, execution_times)“ erstellt anhand der gesammelten Daten ein einfaches Liniendiagramm. Die Werte von „input_sizes“ werden auf der x-Achse angezeigt und repräsentieren unterschiedliche Eingabegrößen. Der Wert von „execution_times“ wird auf der vertikalen Achse angezeigt und stellt die Zeit dar, die zum Ausführen der Funktion „algo_time()“ bei unterschiedlichen Eingabegrößen erforderlich ist.
Abschließend beschriften wir das Koordinatensystem mit „plt.xlabel()“ und „plt.ylabel()“, um die Bedeutung jeder Achse anzuzeigen. Führen Sie als Nächstes die Funktion „plt.show()“ aus, um das Diagramm zu rendern.
Sobald wir das Programm ausführen, zeigt uns die Grafik, wie die Verarbeitungszeit steigt, wenn die Größe der Eingabe ('n') wächst.
Fazit
Zusammenfassend ist die Beherrschung der Zeitkomplexität und Visualisierung in Python mithilfe von Matplotlib eine wertvolle Fähigkeit für jeden Programmierer, der effiziente und optimierte Softwarelösungen erstellen möchte. Wenn wir verstehen, wie sich Algorithmen auf verschiedenen Eingabeskalen verhalten, können wir komplexe Probleme lösen und robuste Anwendungen erstellen, die zeitnah und effizient Ergebnisse liefern.
Das obige ist der detaillierte Inhalt vonVisualisieren Sie O(n) mit Python.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
