 Backend-Entwicklung
Backend-Entwicklung
 C++
C++
 Wie groß ist die Fläche der größtmöglichen Raute, die in ein Rechteck eingeschrieben werden kann?
Wie groß ist die Fläche der größtmöglichen Raute, die in ein Rechteck eingeschrieben werden kann?
Wie groß ist die Fläche der größtmöglichen Raute, die in ein Rechteck eingeschrieben werden kann?

Die in ein Rechteck eingeschriebene Raute verläuft tangential zu den Seiten des Rechtecks, sodass wir daraus schließen können, dass die Diagonale der größten eingeschriebenen Raute gleich der Länge und Breite des Rechtecks ist.
Wenn wir die Länge (l) und Breite (b) des Rechtecks haben, sind die Diagonallängen der größten eingeschriebenen Raute d1 = l und d2 = b.
Die Fläche einer Raute ergibt sich aus der Formel
Area = (d1*d2)/2
Ersetzen wir die Werte von d1 und d2, erhalten wir:
Area = (l*b)/2
Mit dieser Formel können wir ein Programm erstellen, das die Fläche von berechnet die größte Raute, die in ein Rechteck eingeschrieben werden kann,
Beispiel
Echtzeitdemonstration
#include <stdio.h>
int main() {
float l = 16, b = 6;
float area = (l*b)/2;
printf("The area of rhombus inscribed in a rectangle of length %f and breadth %f is %f", l,b,area);
return 0;
}Ausgabe
The area of rhombus inscribed in a rectangle of length 15 and breadth 12 is 90.
Das obige ist der detaillierte Inhalt vonWie groß ist die Fläche der größtmöglichen Raute, die in ein Rechteck eingeschrieben werden kann?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Wie groß ist die Fläche eines Kreises, der in eine Raute eingeschrieben ist?
Sep 05, 2023 am 08:25 AM
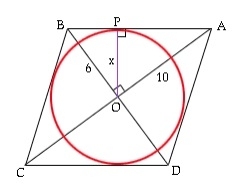
Wie groß ist die Fläche eines Kreises, der in eine Raute eingeschrieben ist?
Sep 05, 2023 am 08:25 AM
Der eingeschriebene Kreis einer Raute tangiert ihre vier Seiten und vier Endpunkte. Die Seiten der Raute berühren den Kreis. Hier ist r der Radius, der mithilfe von a und der Diagonale des angegebenen Werts ermittelt wird. Nun ist das Flächendreieck AOB = ½*OA*OB = ½*AB*r (beide verwenden die Formel ½*b*h). ½*a/2*b/2=½*(√(a2/4+b2/4))*ra*b/8=√(a2+b2)*r/4r=a*b/2√(a2 +b2) Kreisfläche = π*r*r=π*(a2*b2)/4(a2support>+b2) Beispiel für die Diagonalen der Raute 5 und 10. Die Fläche beträgt 15,700000. Beispielcode. Echtzeitdemonstration #include<stdio.h>intma
 Wie groß ist die Fläche eines Kreises innerhalb eines Rechtecks, das in einen Halbkreis eingeschrieben ist?
Sep 13, 2023 am 08:45 AM
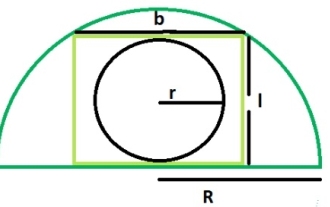
Wie groß ist die Fläche eines Kreises innerhalb eines Rechtecks, das in einen Halbkreis eingeschrieben ist?
Sep 13, 2023 am 08:45 AM
Ein in ein Rechteck eingeschriebener Kreis tangiert die längere Seite des Rechtecks, d. h. seine Länge tangiert den Kreis. Ein in einen Halbkreis eingeschriebenes Rechteck berührt zwei Punkte auf dem Bogen des Halbkreises. Die Breite des Rechtecks entspricht dem Durchmesser des Kreises. Wenn R der Radius des Halbkreises ist. Die Länge des Rechtecks = √2R/2 Die Breite des Rechtecks = R/√2 Der Radius des eingeschriebenen Kreises beträgt r = b/2 = R/2√2 Mit dieser Formel können wir das in den Halbkreis eingeschriebene Rechteck berechnen Die Fläche eines Kreises, Fläche = (π*r2)=π*R/8 Beispieldemonstration #include<stdio.h>intmain(){&
 So führen Sie eine Grafik zusammen, nachdem CAD-Rechtecke verstreut sind
Feb 28, 2024 pm 12:10 PM
So führen Sie eine Grafik zusammen, nachdem CAD-Rechtecke verstreut sind
Feb 28, 2024 pm 12:10 PM
Bei der Verwendung von CAD-Software kommt es häufig vor, dass wir „verstreute“ rechteckige Objekte wieder zu einer einzigen Grafik zusammenfügen müssen. Dieser Bedarf entsteht in vielen Bereichen, beispielsweise in der Raumplanung, im mechanischen Design und in Architekturzeichnungen. Um dieser Nachfrage gerecht zu werden, müssen wir einige Schlüsselfunktionen der CAD-Software verstehen und beherrschen. Als Nächstes stellt Ihnen der Herausgeber dieser Website ausführlich vor, wie Sie diese Aufgabe in der CAD-Umgebung ausführen. Benutzer, die Zweifel haben, können diesem Artikel folgen, um mehr zu erfahren. Methode zum Zusammenführen von CAD-Rechtecken zu einer Grafik nach dem Aufteilen: 1. Öffnen Sie die CAD2023-Software, erstellen Sie ein Rechteck und geben Sie dann den X-Befehl und ein Leerzeichen ein. Wie unten gezeigt: 2. Wählen Sie das rechteckige Objekt aus und platzieren Sie es. Sie können die Objekte aufteilen. 3. Wählen Sie alle offenen Leitungen aus
 Schreiben Sie ein Programm in C-Sprache, um Voll- und Hohlrautenmuster zu drucken
Aug 29, 2023 am 09:33 AM
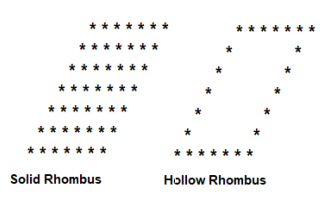
Schreiben Sie ein Programm in C-Sprache, um Voll- und Hohlrautenmuster zu drucken
Aug 29, 2023 am 09:33 AM
Programmbeschreibung Drucken Sie das Muster einer massiven und hohlen Raute wie unten gezeigt
 Was ist das größte Quadrat, das in ein gleichseitiges Dreieck eingeschrieben werden kann?
Sep 22, 2023 pm 06:21 PM
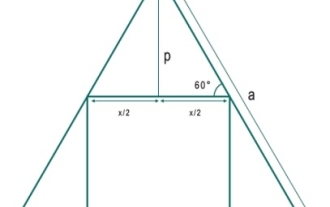
Was ist das größte Quadrat, das in ein gleichseitiges Dreieck eingeschrieben werden kann?
Sep 22, 2023 pm 06:21 PM
Hier sehen wir die Fläche des größten Quadrats, das in ein gleichseitiges Dreieck eingeschrieben werden kann. Die Seitenlänge des Dreiecks ist „a“ und die Seitenlänge des Quadrats ist x. Die Seitenlänge „a“ des Dreiecks beträgt − also ist x − Beispiel #include<iostream>#include<cmath>usingnamespacestd;floatareaSquare(floata){//aissideoftriangle if(a<0)//ifaisnegative,thenthisisi
 Schreiben Sie ein Java-Programm, um die Fläche und den Umfang eines Rechtecks mithilfe des Klassenkonzepts zu berechnen
Sep 03, 2023 am 11:37 AM
Schreiben Sie ein Java-Programm, um die Fläche und den Umfang eines Rechtecks mithilfe des Klassenkonzepts zu berechnen
Sep 03, 2023 am 11:37 AM
Die Java-Sprache ist heute eine der am häufigsten verwendeten objektorientierten Programmiersprachen der Welt. Das Konzept der Klassen ist eines der wichtigsten Merkmale objektorientierter Sprachen. Eine Klasse ist wie eine Blaupause für ein Objekt. Wenn wir zum Beispiel ein Haus bauen wollen, erstellen wir zunächst einen Bauplan des Hauses, also einen Plan, der zeigt, wie wir das Haus bauen werden. Nach diesem Plan können wir viele Häuser bauen. Ebenso können wir mithilfe von Klassen viele Objekte erstellen. Klassen sind Blaupausen für die Erstellung vieler Objekte, wobei Objekte reale Einheiten wie Autos, Fahrräder, Stifte usw. sind. Eine Klasse hat die Eigenschaften aller Objekte und die Objekte haben die Werte dieser Eigenschaften. In diesem Artikel schreiben wir ein Java-Programm, um den Umfang und die Flächen eines Rechtecks mithilfe des Klassenkonzepts zu ermitteln
 Wie drucke ich Sterne in einem Rautenmuster mit der Sprache C?
Sep 03, 2023 pm 02:41 PM
Wie drucke ich Sterne in einem Rautenmuster mit der Sprache C?
Sep 03, 2023 pm 02:41 PM
Um hier Sterne in einem Rautenmuster zu drucken, verwenden wir verschachtelte For-Schleifen. Die Logik, die wir verwenden, um Sterne in einem Rautenmuster zu drucken, ist wie folgt: //Forupperhalfofthediamondthelogicis:for(j=1;j<=rows;j++){ for(i=1;i<=rows-j;i++) printf( " "); for(i=1;i<=2*j-1;i++
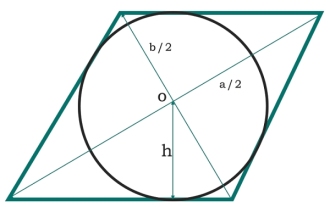 Wie groß ist im C-Programm die Fläche eines Kreises, der in eine Raute eingeschrieben ist?
Sep 01, 2023 pm 09:29 PM
Wie groß ist im C-Programm die Fläche eines Kreises, der in eine Raute eingeschrieben ist?
Sep 01, 2023 pm 09:29 PM
Hier sehen wir die Fläche eines Kreises, der in eine Raute eingeschrieben ist. Die Diagonalen der Raute sind „a“ bzw. „b“. Der Radius des Kreises beträgt h. Zwei Diagonalen bilden vier gleiche Dreiecke. Jedes Dreieck ist ein rechtwinkliges Dreieck, also ist ihre Fläche - Jede Seite der Raute ist die Hypotenuse - Daher ist die Fläche des Kreises - Beispiel#include<iostream>#include<cmath>usingnamespacestd;floatarea(floata,floatb ) { if(a<0||b<0)//ifthevaluesaren





