Die Anzahl gleichschenkliger Dreiecke in einem Binärbaum
Ein Binärbaum ist eine Datenstruktur, in der jeder Knoten bis zu zwei untergeordnete Knoten haben kann. Diese Kinder werden linke Kinder bzw. rechte Kinder genannt. Angenommen, wir erhalten eine übergeordnete Array-Darstellung, Sie müssen diese verwenden, um einen Binärbaum zu erstellen. Ein Binärbaum kann mehrere gleichschenklige Dreiecke haben. Wir müssen die Gesamtzahl der möglichen gleichschenkligen Dreiecke in diesem Binärbaum ermitteln.
In diesem Artikel werden wir verschiedene Techniken zur Lösung dieses Problems in C++ untersuchen.
Das Problem verstehen
Gibt Ihnen ein übergeordnetes Array. Sie müssen es in Form eines Binärbaums darstellen, sodass der Array-Index den Wert des Baumknotens bildet und der Wert im Array den übergeordneten Knoten dieses bestimmten Index angibt.
Bitte beachten Sie, dass -1 immer der übergeordnete Root-Knoten ist. Nachfolgend finden Sie ein Array und seine binäre Baumdarstellung.
Parent array = [0, -1, 3, 1, 1, 2, 2, 3, 4, 4]
Binärbaum -
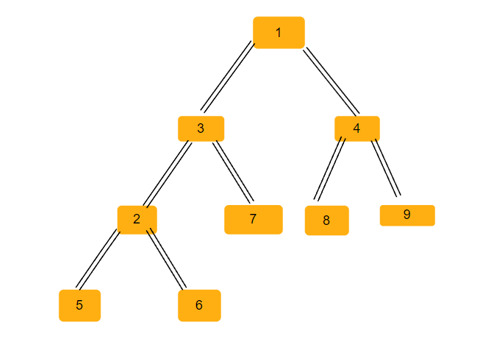
In jedem Binärbaum können wir drei Arten gleichschenkliger Dreiecke haben -
Linkes gleichschenkliges Dreieck − In diesem Dreieck ist der Scheitelpunkt ein untergeordneter Knoten des linken übergeordneten Knotens, und die Scheitelpunkte, die die Basis bilden (beide Seiten des gleichschenkligen Dreiecks), sind links untergeordneter Knoten. Untergeordnete Knoten können direkt oder indirekt sein. Im Baum oben haben wir zwei solcher gleichschenkligen Dreiecke – (2, 6, 3), (3, 7, 1).
Rechtsgleichschenkliges Dreieck − In diesem Dreieck ist der Scheitelpunkt das rechte Kind des Elternteils, während der Scheitelpunkt, der die Basis bildet, das rechte Kind des Scheitelpunkts ist. Kinder können direkt oder indirekt sein. Im Baum oben haben wir nur ein solches gleichschenkliges Dreieck (4, 1, 8).
Ausgeglichenes gleichschenkliges Dreieck − In diesem Dreieck sind die Scheitelpunkte, die die Basis bilden, die linken und rechten untergeordneten Knoten des Scheitelpunktknotens. Im obigen Baum haben wir fünf solcher gleichschenkligen Dreiecke (1, 3, 4), (3, 2, 7), (4, 8, 9), (2, 5, 6), (1, 2, 9).
Für den obigen Binärbaum haben wir also insgesamt 8 gleichschenklige Dreiecke.
Durchquerung mit Tiefensuche
Depth First Search (DFS) ist eine Methode zum Tiefendurchsuchen aller Knoten eines Baums. Es beginnt am Wurzelknoten, bewegt sich zu jedem Zweig und geht dann zurück.
Zuerst verwenden wir DFS, um jeden Knoten des Binärbaums zu durchlaufen und ihn in ein Diagramm umzuwandeln, sodass jeder Knoten als nebeneinander dargestellt dargestellt wird. Dies erleichtert die Durchquerung.
Für jeden Knoten prüfen wir, ob er untergeordnete Knoten hat. Nach der Überprüfung sortieren wir sie mit der Funktion sort(node[x].begin(), node[x].end()).
Als nächstes prüfen wir, ob der aktuelle Knoten der linke oder rechte Nachfolger seines entsprechenden übergeordneten Knotens ist. Wir verwenden die DFS-Funktion rekursiv auf allen Knoten des Binärbaums.
Wenn der aktuelle Knoten zwei Kinder hat (direkt oder indirekt), prüfen wir die Möglichkeit, dass ein gleichschenkliges Dreieck existiert, indem wir die Kanten zwischen ihnen berechnen. Wir finden die Kanten zwischen ihnen mithilfe der Funktion graph, die im folgenden Code angegeben ist.
Abschließend berechnen wir die Gesamtzahl der gleichschenkligen Dreiecke, indem wir alle möglichen Dreiecke in verschiedenen Positionen addieren.
Beispiel
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
#define MAX int(1e5)
vector < int > * node;
int right_down[MAX];
int right_up[MAX];
int left_down[MAX];
int left_up[MAX];
// DFS traversal over a node
void DFS(int x, int * parent) {
// Check if adjacent nodes are present for node x
if (node[x].size() != 0)
sort(node[x].begin(), node[x].end());
// Check whether the node has a parent node
if (parent[x] != -1) {
int indexOfParent = parent[x];
int childrenCount = node[indexOfParent].size();
if (childrenCount > 1) {
int parentFirstChild = node[indexOfParent][0];
// Check if current node is left node of the parent
if (x == parentFirstChild) {
right_up[x] += right_up[indexOfParent] + 1;
// Check if current node is right node of the parent
} else {
left_up[x] += left_up[indexOfParent] + 1;
}
} else {
right_up[x] += right_up[indexOfParent] + 1;
}
}
// Iterate over children of current node
for (int i = 0; i < node[x].size(); ++i) {
int y = node[x][i];
DFS(y, parent);
// left child of current node
if (i == 0) {
left_down[x] += left_down[y] + 1;
}
// right child of current node
else {
right_down[x] += right_down[y] + 1;
}
}
}
int graph(int * parent, int N) {
int rootNode;
node = new vector < int > [N];
for (int i = 0; i < N; ++i) {
if (parent[i] != -1) {
node[parent[i]].push_back(i);
} else {
rootNode = i;
}
left_up[i] = 0;
right_up[i] = 0;
left_down[i] = 0;
right_down[i] = 0;
}
return rootNode;
}
int main() {
int N = 10;
int parent[] = { 0, -1, 3, 1, 1, 2, 2, 3, 4, 4 };
int rootNode = graph(parent, N);
DFS(rootNode, parent);
int count = 0;
// Counting the total isosceles triangles
for (int i = 0; i < N; ++i) {
count += min(right_down[i], right_up[i]);
count += min(left_down[i], left_up[i]);
count += min(left_down[i], right_down[i]);
}
cout << "Number of isosceles triangles in the binary tree are " <<
count;
return 0;
}
Ausgabe
Number of isosceles triangles in the binary tree are 8
Fazit
Wir haben besprochen, wie man die Gesamtzahl der gleichseitigen Dreiecke in einem Binärbaum ermittelt, wenn ein übergeordnetes Array gegeben ist. Wir können dies erreichen, indem wir die Tiefensuche verwenden, die es uns ermöglicht, einen Binärbaum zu durchlaufen.
Das obige ist der detaillierte Inhalt vonDie Anzahl gleichschenkliger Dreiecke in einem Binärbaum. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Erweitern Sie Ihr Wissen! Maschinelles Lernen mit logischen Regeln
Apr 01, 2023 pm 10:07 PM
Erweitern Sie Ihr Wissen! Maschinelles Lernen mit logischen Regeln
Apr 01, 2023 pm 10:07 PM
Auf der Precision-Recall-Kurve werden dieselben Punkte mit unterschiedlichen Achsen aufgetragen. Warnung: Der erste rote Punkt links (0 % Rückruf, 100 % Präzision) entspricht 0 Regeln. Der zweite Punkt links ist die erste Regel und so weiter. Skope-rules verwendet ein Baummodell, um Regelkandidaten zu generieren. Erstellen Sie zunächst einige Entscheidungsbäume und betrachten Sie die Pfade vom Wurzelknoten zu internen Knoten oder Blattknoten als Regelkandidaten. Diese Kandidatenregeln werden dann nach einigen vordefinierten Kriterien wie Präzision und Rückruf gefiltert. Nur diejenigen, deren Präzision und Erinnerung über ihren Schwellenwerten liegen, werden beibehalten. Abschließend wird eine Ähnlichkeitsfilterung angewendet, um Regeln mit ausreichender Diversität auszuwählen. Im Allgemeinen werden Skope-Regeln angewendet, um die Ursache jedes einzelnen Problems herauszufinden
 OpenOOD-Update v1.5: umfassende und genaue Bibliothek und Testplattform zur Erkennung von Out-of-Distribution-Codes, die Online-Rankings und One-Click-Tests unterstützt
Jul 03, 2023 pm 04:41 PM
OpenOOD-Update v1.5: umfassende und genaue Bibliothek und Testplattform zur Erkennung von Out-of-Distribution-Codes, die Online-Rankings und One-Click-Tests unterstützt
Jul 03, 2023 pm 04:41 PM
Die Out-of-Distribution (OOD)-Erkennung ist für den zuverlässigen Betrieb offener intelligenter Systeme von entscheidender Bedeutung, aktuelle objektorientierte Erkennungsmethoden leiden jedoch unter „Bewertungsinkonsistenzen“ (Bewertungsinkonsistenzen). Frühere Arbeiten OpenOODv1 vereinheitlichen die Auswertung der OOD-Erkennung, weisen jedoch immer noch Einschränkungen hinsichtlich Skalierbarkeit und Benutzerfreundlichkeit auf. Kürzlich hat das Entwicklungsteam erneut OpenOODv1.5 vorgeschlagen. Im Vergleich zur Vorgängerversion wurde die Bewertung der neuen OOD-Erkennungsmethode erheblich verbessert, um Genauigkeit, Standardisierung und Benutzerfreundlichkeit zu gewährleisten. Bildpapier: https://arxiv.org/abs/2306.09301OpenOODCodebase:htt
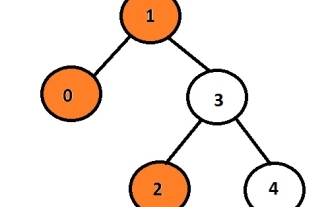 Drucken Sie die linke Ansicht des Binärbaums in C-Sprache
Sep 03, 2023 pm 01:25 PM
Drucken Sie die linke Ansicht des Binärbaums in C-Sprache
Sep 03, 2023 pm 01:25 PM
Die Aufgabe besteht darin, den linken Knoten des angegebenen Binärbaums zu drucken. Zuerst fügt der Benutzer Daten ein, wodurch ein Binärbaum erstellt wird, und druckt dann die linke Ansicht des resultierenden Baums aus. Jeder Knoten kann höchstens 2 untergeordnete Knoten haben, sodass dieses Programm nur über den mit dem Knoten verknüpften linken Zeiger iterieren darf. Wenn der linke Zeiger nicht null ist, bedeutet dies, dass ihm einige Daten oder ein Zeiger zugeordnet sind, andernfalls wird er als gedruckt und angezeigt das linke untergeordnete Element der Ausgabe. BeispielEingabe:10324Ausgabe:102Hier repräsentiert der orangefarbene Knoten die linke Ansicht des Binärbaums. In der angegebenen Grafik ist der Knoten mit den Daten 1 der Wurzelknoten, daher wird er gedruckt und anstatt zum linken untergeordneten Knoten zu gehen, wird er 0 drucken und dann geht er zu 3 und gibt seinen linken untergeordneten Knoten aus, der 2 ist. Wir können eine rekursive Methode verwenden, um die Knotenebene zu speichern
 Detaillierte Erläuterung der binären Baumstruktur in Java
Jun 16, 2023 am 08:58 AM
Detaillierte Erläuterung der binären Baumstruktur in Java
Jun 16, 2023 am 08:58 AM
Binärbäume sind eine gängige Datenstruktur in der Informatik und eine häufig verwendete Datenstruktur in der Java-Programmierung. In diesem Artikel wird die Binärbaumstruktur in Java ausführlich vorgestellt. 1. Was ist ein Binärbaum? In der Informatik ist ein Binärbaum eine Baumstruktur, in der jeder Knoten höchstens zwei untergeordnete Knoten hat. Unter diesen ist der linke untergeordnete Knoten kleiner als der übergeordnete Knoten und der rechte untergeordnete Knoten größer als der übergeordnete Knoten. In der Java-Programmierung werden Binärbäume häufig verwendet, um das Sortieren und Suchen darzustellen und die Effizienz der Datenabfrage zu verbessern. 2. Implementierung eines Binärbaums in Java In Java ein Binärbaum
 Wie finde ich die Anzahl der von der Laufzeit in Java bereitgestellten Parameter?
Sep 23, 2023 pm 01:13 PM
Wie finde ich die Anzahl der von der Laufzeit in Java bereitgestellten Parameter?
Sep 23, 2023 pm 01:13 PM
In Java besteht eine Möglichkeit, Parameter zur Laufzeit zu übergeben, darin, die Befehlszeile oder das Terminal zu verwenden. Beim Abrufen dieser Werte für Befehlszeilenparameter müssen wir möglicherweise die Anzahl der vom Benutzer zur Laufzeit bereitgestellten Parameter ermitteln, was mithilfe des Längenattributs erreicht werden kann. Ziel dieses Artikels ist es, den Prozess des Übergebens und Abrufens einer vom Benutzer bereitgestellten Anzahl von Parametern mithilfe eines Beispielprogramms zu erläutern. Ermitteln Sie die Anzahl der vom Benutzer zur Laufzeit bereitgestellten Argumente. Bevor wir die Anzahl der Befehlszeilenargumente ermitteln, besteht unser erster Schritt darin, ein Programm zu erstellen, das dem Benutzer die Übergabe von Argumenten zur Laufzeit ermöglicht. String[]-Parameter Beim Schreiben von Java-Programmen stoßen wir häufig auf die Methode main(). Wenn die JVM diese Methode aufruft, beginnt die Ausführung der Java-Anwendung. Es wird mit einem Argument namens String[]args verwendet
 Linux-Befehl: So überprüfen Sie die Anzahl der Telnet-Prozesse
Mar 01, 2024 am 11:39 AM
Linux-Befehl: So überprüfen Sie die Anzahl der Telnet-Prozesse
Mar 01, 2024 am 11:39 AM
Linux-Befehle sind eines der unverzichtbaren Werkzeuge in der täglichen Arbeit von Systemadministratoren. Sie können uns bei der Erledigung verschiedener Systemverwaltungsaufgaben helfen. Bei Betriebs- und Wartungsarbeiten ist es manchmal notwendig, die Nummer eines bestimmten Prozesses im System zu überprüfen, um Probleme zu erkennen und rechtzeitig Anpassungen vorzunehmen. In diesem Artikel wird erläutert, wie Sie mithilfe von Linux-Befehlen die Anzahl der Telnet-Prozesse überprüfen. Lassen Sie uns gemeinsam lernen. In Linux-Systemen können wir den Befehl ps in Kombination mit dem Befehl grep verwenden, um die Anzahl der Telnet-Prozesse anzuzeigen. Zuerst müssen wir ein Terminal öffnen,
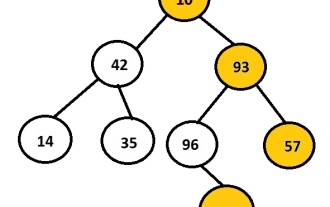 Drucken Sie in der Sprache C die rechte Ansicht des Binärbaums
Sep 16, 2023 pm 11:13 PM
Drucken Sie in der Sprache C die rechte Ansicht des Binärbaums
Sep 16, 2023 pm 11:13 PM
Die Aufgabe besteht darin, den rechten Knoten des angegebenen Binärbaums zu drucken. Zuerst fügt der Benutzer Daten ein, um einen Binärbaum zu erstellen, und druckt dann eine rechte Ansicht des resultierenden Baums. Das Bild oben zeigt einen Binärbaum, der mit den Knoten 10, 42, 93, 14, 35, 96, 57 und 88 erstellt wurde, wobei die Knoten auf der rechten Seite des Baums ausgewählt und angezeigt werden. Beispielsweise sind 10, 93, 57 und 88 die Knoten ganz rechts im Binärbaum. Beispieleingabe: 1042931435965788 Ausgabe: 10935788 Jeder Knoten hat zwei Zeiger, den linken Zeiger und den rechten Zeiger. Gemäß dieser Frage muss das Programm nur den richtigen Knoten durchlaufen. Daher muss das linke Kind des Knotens nicht berücksichtigt werden. In der rechten Ansicht werden alle Knoten gespeichert, die der letzte Knoten in ihrer Hierarchie sind. Deshalb können wir
 Schreiben Sie mit C++ einen Code, um die Anzahl der Subarrays mit denselben Mindest- und Höchstwerten zu ermitteln
Aug 25, 2023 pm 11:33 PM
Schreiben Sie mit C++ einen Code, um die Anzahl der Subarrays mit denselben Mindest- und Höchstwerten zu ermitteln
Aug 25, 2023 pm 11:33 PM
In diesem Artikel werden wir C++ verwenden, um das Problem zu lösen, die Anzahl der Subarrays zu ermitteln, deren Maximal- und Minimalwert gleich sind. Das Folgende ist ein Beispiel für das Problem: −Input:array={2,3,6,6,2,4,4,4}Output:12Explanation:{2},{3},{6},{6}, {2 },{4},{4},{4},{6,6},{4,4},{4,4}und {4,4,4}sind die Teilarrays, die mit dem gleichen maximalen und minimalen Element gebildet werden können. Eingabe: array={3, 3, 1,5,




