Hilfsraum für rekursive Funktionen im C-Programm verwenden?

Hier werden wir sehen, wie rekursive Funktionsaufrufe Hilfsraum benötigen. Wie unterscheidet es sich von einem normalen Funktionsaufruf?
Angenommen, wir haben eine Funktion wie unten gezeigt -
long fact(int n){
if(n == 0 || n == 1)
return 1;
return n * fact(n-1);
}Diese Funktion ist eine rekursive Funktion. Wenn wir es wie fact(5) aufrufen, speichert es die Adresse wie unten gezeigt im Stapel. -
fact(5) ---> fact(4) ---> fact(3) ---> fact(2) ---> fact(1)
Wenn sich die rekursive Funktion immer wieder selbst aufruft, wird die Adresse dem Stapel hinzugefügt. Wenn die Funktion also n-mal rekursiv aufgerufen wird, belegt sie O(n) Hilfsraum. Dies bedeutet jedoch nicht, dass die Raumkomplexität O(n) beträgt, wenn eine Normalfunktion n-mal aufgerufen wird. Bei normalen Funktionen wird die Adresse beim Aufruf auf den Stapel gelegt. Sobald der Vorgang abgeschlossen ist, wird die Adresse vom Stapel entfernt und in die Aufruffunktion eingegeben. Dann rufen Sie noch einmal an. Seine Komplexität ist also O(1).
Das obige ist der detaillierte Inhalt vonHilfsraum für rekursive Funktionen im C-Programm verwenden?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Übersetzen Sie Folgendes ins Chinesische: C-Programm zur Konvertierung römischer Ziffern in Dezimalzahlen
Sep 05, 2023 pm 09:53 PM
Übersetzen Sie Folgendes ins Chinesische: C-Programm zur Konvertierung römischer Ziffern in Dezimalzahlen
Sep 05, 2023 pm 09:53 PM
Nachfolgend finden Sie einen C-Sprachalgorithmus zum Konvertieren römischer Ziffern in Dezimalzahlen: Algorithmus Schritt 1 – Start Schritt 2 – Römische Ziffern zur Laufzeit lesen Schritt 3 – Länge: = strlen(roman) Schritt 4 – Für i=0 bis Länge-1 Schritt 4.1-switch(roman[i]) Schritt 4.1.1-case'm': &nbs
 Welche Optimierungstechniken gibt es für rekursive C++-Funktionen?
Apr 17, 2024 pm 12:24 PM
Welche Optimierungstechniken gibt es für rekursive C++-Funktionen?
Apr 17, 2024 pm 12:24 PM
Um die Leistung rekursiver Funktionen zu optimieren, können Sie die folgenden Techniken verwenden: Verwenden Sie die Endrekursion: Platzieren Sie rekursive Aufrufe am Ende der Funktion, um rekursiven Overhead zu vermeiden. Auswendiglernen: Berechnete Ergebnisse speichern, um wiederholte Berechnungen zu vermeiden. Methode „Teile und herrsche“: Zerlegen Sie das Problem und lösen Sie die Teilprobleme rekursiv, um die Effizienz zu verbessern.
 C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird
Sep 17, 2023 am 10:49 AM
C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird
Sep 17, 2023 am 10:49 AM
Hyperbelfunktionen werden mithilfe von Hyperbeln anstelle von Kreisen definiert und entsprechen gewöhnlichen trigonometrischen Funktionen. Es gibt den Verhältnisparameter in der hyperbolischen Sinusfunktion aus dem angegebenen Winkel im Bogenmaß zurück. Aber machen Sie das Gegenteil, oder anders gesagt. Wenn wir einen Winkel aus einem hyperbolischen Sinus berechnen wollen, benötigen wir eine umgekehrte hyperbolische trigonometrische Operation wie die hyperbolische Umkehrsinusoperation. In diesem Kurs wird gezeigt, wie Sie die hyperbolische Umkehrsinusfunktion (asinh) in C++ verwenden, um Winkel mithilfe des hyperbolischen Sinuswerts im Bogenmaß zu berechnen. Die hyperbolische Arkussinusoperation folgt der folgenden Formel -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Wo\:In\:ist\:natürlicher Logarithmus\:(log_e\:k)
 C-Programm zum Ermitteln der Länge einer verknüpften Liste
Sep 07, 2023 pm 07:33 PM
C-Programm zum Ermitteln der Länge einer verknüpften Liste
Sep 07, 2023 pm 07:33 PM
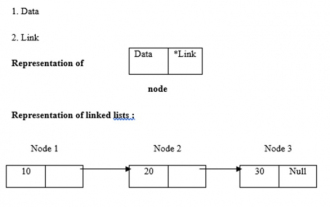
Verknüpfte Listen verwenden eine dynamische Speicherzuweisung, d. h. sie wachsen und schrumpfen entsprechend. Sie werden als Ansammlungen von Knoten definiert. Hier besteht ein Knoten aus zwei Teilen: Daten und Links. Die Darstellung von Daten, Links und verknüpften Listen ist wie folgt: - Arten von verknüpften Listen Es gibt vier Arten von verknüpften Listen: - Einfach verknüpfte Liste / Einfach verknüpfte Liste Doppelt / Doppelt verknüpfte Liste Zirkuläre einfach verknüpfte Liste Zirkuläre doppelt verknüpfte Liste Wir Verwenden Sie die rekursive Methode, um die Länge der verknüpften Liste zu ermitteln. Die Logik lautet -intlength(node *temp){ if(temp==NULL) returnl;
 C++-Programm zum Drucken eines Wörterbuchs
Sep 11, 2023 am 10:33 AM
C++-Programm zum Drucken eines Wörterbuchs
Sep 11, 2023 am 10:33 AM
Eine Karte ist ein spezieller Containertyp in C++, bei dem jedes Element ein Paar aus zwei Werten ist, nämlich einem Schlüsselwert und einem zugeordneten Wert. Der Schlüsselwert wird zum Indizieren jedes Elements verwendet, und der zugeordnete Wert ist der mit dem Schlüssel verknüpfte Wert. Unabhängig davon, ob der zugeordnete Wert eindeutig ist, ist der Schlüssel immer eindeutig. Um Kartenelemente in C++ zu drucken, müssen wir einen Iterator verwenden. Ein Element in einer Menge von Elementen wird durch ein Iteratorobjekt angegeben. Iteratoren werden hauptsächlich mit Arrays und anderen Arten von Containern (z. B. Vektoren) verwendet und verfügen über einen bestimmten Satz von Operationen, mit denen bestimmte Elemente innerhalb eines bestimmten Bereichs identifiziert werden können. Iteratoren können inkrementiert oder dekrementiert werden, um auf verschiedene Elemente in einem Bereich oder Container zu verweisen. Der Iterator zeigt auf den Speicherort eines bestimmten Elements im Bereich. Drucken einer Karte in C++ mit Iteratoren Schauen wir uns zunächst an, wie man definiert
 Anwendung rekursiver C++-Funktionen in Suchalgorithmen?
Apr 17, 2024 pm 04:30 PM
Anwendung rekursiver C++-Funktionen in Suchalgorithmen?
Apr 17, 2024 pm 04:30 PM
Rekursive Funktionen werden in Suchalgorithmen verwendet, um baumartige Datenstrukturen zu untersuchen. Die Tiefensuche verwendet einen Stapel, um Knoten zu erkunden, während die Breitensuche eine Warteschlange verwendet, um Schicht für Schicht zu durchlaufen. In praktischen Anwendungen, beispielsweise beim Suchen von Dateien, können rekursive Funktionen verwendet werden, um nach einer bestimmten Datei in einem angegebenen Verzeichnis zu suchen.
 Das C-Programm verwendet die Funktion rename(), um den Dateinamen zu ändern
Sep 21, 2023 pm 10:01 PM
Das C-Programm verwendet die Funktion rename(), um den Dateinamen zu ändern
Sep 21, 2023 pm 10:01 PM
Die Umbenennungsfunktion ändert den alten Namen einer Datei oder eines Verzeichnisses in den neuen Namen. Dieser Vorgang ähnelt dem Verschiebevorgang. Wir können diese Umbenennungsfunktion also auch zum Verschieben von Dateien verwenden. Diese Funktion ist in der Headerdatei der stdio.h-Bibliothek vorhanden. Die Syntax der Umbenennungsfunktion lautet wie folgt: intrename(constchar*oldname,constchar*newname); Die Funktion der rename()-Funktion akzeptiert zwei Parameter. Einer ist alter Name und der andere ist neuer Name. Beide Parameter sind Zeiger auf konstante Zeichen, die den alten und neuen Namen der Datei definieren. Gibt Null zurück, wenn die Datei erfolgreich umbenannt wurde; andernfalls wird eine Ganzzahl ungleich Null zurückgegeben. Während eines Umbenennungsvorgangs
 C++-Programm zum Ermitteln des Imaginärteils einer gegebenen komplexen Zahl
Sep 06, 2023 pm 06:05 PM
C++-Programm zum Ermitteln des Imaginärteils einer gegebenen komplexen Zahl
Sep 06, 2023 pm 06:05 PM
Die moderne Wissenschaft stützt sich stark auf das Konzept der Pluralzahlen, das erstmals im frühen 17. Jahrhundert von Girolamo Cardano etabliert und im 16. Jahrhundert eingeführt wurde. Die Formel für komplexe Zahlen lautet a+ib, wobei a den HTML-Code enthält und b eine reelle Zahl ist. Eine komplexe Zahl soll aus zwei Teilen bestehen: dem Realteil <a> und dem Imaginärteil (<ib>). Der Wert von i oder iota ist √-1. Die Pluralklasse in C++ ist eine Klasse zur Darstellung komplexer Zahlen. Die komplexe Klasse in C++ kann mehrere komplexe Zahlenoperationen darstellen und steuern. Werfen wir einen Blick darauf, wie man die Anzeige mehrerer Zahlen darstellt und steuert. Mitgliedsfunktion imag() Wie oben erwähnt, bestehen komplexe Zahlen aus einem Realteil und einem Imaginärteil. Um den Realteil anzuzeigen, verwenden wir real()




