Wie viele Dreiecke gibt es, wenn nicht mehr als zwei Punkte in der Ebene kollinear sind?

Sehen wir uns an, wie man die Anzahl der Dreiecke auf einer Ebene mit n Punkten zählt und die Anzahl der kollinearen Punkte auf nicht mehr als zwei begrenzt.

Das Zählen der Anzahl der Dreiecke in einer Ebene mit nicht mehr als zwei kollinearen Punkten ist ein typisches Problem in der Computergeometrie, die in der Computergrafik, Bildverarbeitung und anderen Bereichen der Informatik angewendet wird.

Beim Erstellen eines 2D-Bildes aus einer 3D-Szene in 3D-Grafiken kann das Problem auftreten, Dreiecke in einer Ebene mit nicht mehr als zwei kollinearen Punkten zu berechnen. In diesem Fall kann der Prozess der Dreieckszählung verwendet werden, um zu bestimmen, wie viele Dreiecke im endgültigen 2D-Bild vorhanden sind, nachdem die 3D-Szene auf eine Ebene projiziert wurde. Dadurch können Sie die Komplexität der Szene bestimmen und die Rendergeschwindigkeit erhöhen.

Bei der Bildverarbeitung möchten wir möglicherweise die Anzahl einzigartiger Objekte oder Formen in einem Bild zählen. Diese Frage ist hilfreich. In diesem Fall können wir das Bild als eine Ansammlung von Punkten auf einer Ebene darstellen und dann die Anzahl der Dreiecke zählen, die zwischen diesen Punkten erstellt werden können, indem wir Dreieckszähltechniken anwenden. Wir können die ungefähre Anzahl verschiedener Elemente oder Formen in einem Bild bestimmen, indem wir die Anzahl der gebildeten Dreiecke zählen.

Anleitung

Lassen Sie uns dieses Problem anhand einiger Beispiele verstehen und versuchen, es zu lösen. ​​

Der Zweck besteht darin, zu bestimmen, wie viele Dreiecke auf einer Ebene mit n Punkten gebildet werden, sodass nicht mehr als zwei Punkte kollinear sind.

Beispiel -

Angenommen, N ist die Anzahl der Punkte auf der Ebene.

N = 3

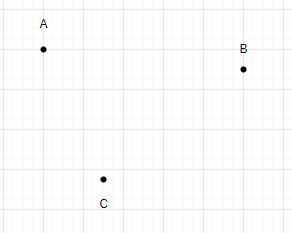
Mit diesen Punkten können wir nur ein Dreieck zeichnen.

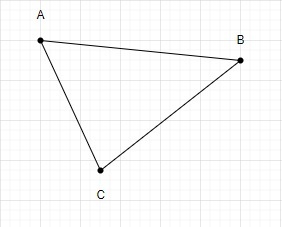
Die Gesamtzahl der Dreiecke, die mit 3 Punkten gebildet werden, beträgt also 1.

Sei N = 4

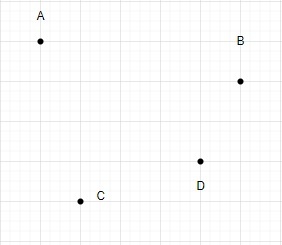
Zeichnen wir mit diesen vier Punkten ein Dreieck.

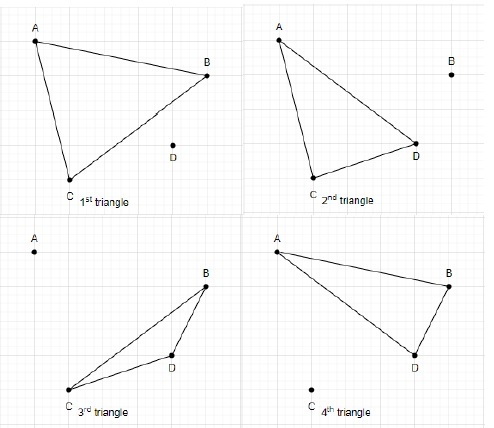
Die Gesamtzahl der aus 4 Punkten gebildeten Dreiecke beträgt 4.

Schauen wir uns einen Teil der Mathematik zur Berechnung der Anzahl der Dreiecke an. Dies kann durch Permutationen und Kombinationen erreicht werden. Um ein Dreieck zu bilden, benötigen Sie jeweils 3 Punkte der Gesamtsumme.

Wenn also eine Ebene n Punkte enthält und nicht mehr als zwei davon kollinear sind, dann ergibt sich die Anzahl der Dreiecke in der Ebene durch die folgende Formel.

$$mathrm{n_{C_{3}}:=:frac{n(n-1):(n-2)}{6}}$$

Methode

Das Programm ermittelt mithilfe des folgenden Algorithmus die Anzahl der Dreiecke in der Ebene, wenn nicht mehr als zwei Punkte kollinear sind.

• Nehmen Sie die Anzahl der Punkte auf der Ebene als Eingabe und beschränken Sie sie auf nicht mehr als zwei kollineare Punkte.

• Berechnen Sie die Gesamtzahl der Dreiecke mithilfe der obigen Formel.

• Drucken Sie die Gesamtzahl der Dreiecke als Ausgabe aus.

Beispiel

C++-Programm zur Berechnung der Anzahl der Dreiecke in einer Ebene, wenn nicht mehr als zwei Punkte kollinear sind.

#include <iostream>
using namespace std;

int main() {
   int number_of_points = 4;
   int number_of_triangle;
   
   number_of_triangle = number_of_points * (number_of_points - 1) * (number_of_points - 2) / 6;
   cout << "Total number of triangles formed using " << number_of_points<< " points = " <<  number_of_triangle << endl;
   
   return 0;
}

Ausgabe

Total number of triangles formed using 4 points = 4

Komplexität

Zeitkomplexität: O(1), da dieser Code unabhängig von der Eingabegröße eine feste Anzahl von Berechnungen durchführt.

Raumkomplexität: O(1), da der Code unabhängig von der Größe der Eingabe eine feste Anzahl von Variablen zum Speichern von Eingabewerten und Ergebnissen verwendet.

Fazit

In diesem Artikel versuchen wir, die Methode zu erklären, mit der man die Gesamtzahl möglicher Dreiecke mit n gegebenen Punkten ermitteln kann, mit der Einschränkung, dass keine zwei Punkte kollinear sind. Ich hoffe, dass dieser Artikel Ihnen hilft, dieses Konzept besser kennenzulernen.

Das obige ist der detaillierte Inhalt vonWie viele Dreiecke gibt es, wenn nicht mehr als zwei Punkte in der Ebene kollinear sind?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!