C++-Programm zum Ermitteln der maximalen Bewertungskomponente, die aus einem Diagramm reduziert werden kann

Angenommen, es gibt einen gewichteten ungerichteten Graphen mit n Eckpunkten und m Kanten. Der Score eines Graphen ist definiert als die Summe der Gewichte aller Kanten im Graphen. Kantengewichte können negativ sein. Wenn sie entfernt werden, erhöht sich die Bewertung des Diagramms. Was wir tun müssen, ist, die Punktzahl des Diagramms zu minimieren, indem wir Kanten im Diagramm entfernen und gleichzeitig die Konnektivität des Diagramms beibehalten. Wir müssen die maximale Punktzahl finden, die reduziert werden kann.

Der Graph wird in Form eines Arrays „Kanten“ angegeben, wobei jedes Element die Form {Gewicht, {Vertex1, Vertex2}} hat.

Wenn also die Eingabe n = 5, m = 6, Kanten = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3 ist , {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}, dann ist die Ausgabe 4.

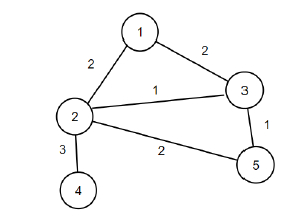
Wenn wir die Kanten (1, 2) und (2, 5) aus dem Diagramm entfernen, beträgt die Gesamtpunktzahlreduzierung 4 und das Diagramm bleibt weiterhin verbunden.

Um dieses Problem zu lösen, werden wir die folgenden Schritte ausführen:

cnum := 0
Define an array par of size: 100.
Define an array dim of size: 100.
Define a function make(), this will take v,
   par[v] := v
   dim[v] := 1
Define a function find(), this will take v,
   if par[v] is same as v, then:
      return v
   return par[v] = find(par[v])
Define a function unify(), this will take a, b,
a := find(a)
b := find(b)
if a is not equal to b, then:
   (decrease cnum by 1)
   if dim[a] > dim[b], then:
      swap values of (a, b)
   par[a] := b
   dim[b] := dim[b] + dim[a]
cnum := n
sort the array edges based on edge weights
for initialize i := 1, when i <= n, update (increase i by 1), do:
   make(i)
res := 0
for each edge in edges, do:
   a := first vertex of edge
   b := second vertex of edge
   weight := weight of edge
   if find(a) is same as find(b), then:
      if weight >= 0, then:
         res := res + 1 * weight
      Ignore following part, skip to the next iteration
   if cnum is same as 1, then:
      if weight >= 0, then:
         res := res + 1 * weight
   Otherwise
      unify(a, b)
return res

Beispiel

Sehen wir uns zum besseren Verständnis die folgende Implementierung an:

#include <bits/stdc++.h>
using namespace std;

int cnum = 0;
int par[100];
int dim[100];

void make(int v){
   par[v] = v;
   dim[v] = 1;
}
int find(int v){
   if(par[v] == v)
   return v;
   return par[v] = find(par[v]);
}
void unify(int a, int b){
   a = find(a); b = find(b);
   if(a != b){
      cnum--; if(dim[a] > dim[b]){
         swap(a, b);
      }
      par[a] = b; dim[b] += dim[a];
   }
}
int solve(int n, int m, vector <pair <int, pair<int,int>>> edges){
   cnum = n;
   sort(edges.begin(), edges.end());
   for(int i = 1; i <= n; i++)
      make(i);
   int res = 0;
   for(auto &edge : edges){
      int a = edge.second.first;
      int b = edge.second.second;
      int weight = edge.first;
      if(find(a) == find(b)) {
         if(weight >= 0) 
            res += 1 * weight;
         continue;
      }
      if(cnum == 1){
         if(weight >= 0)
            res += 1 * weight;
      } else{
         unify(a, b);
      }
   }
   return res;
}
int main() {
   int n = 5, m = 6;
   vector <pair<int, pair<int,int>>> edges = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}};
   cout<< solve(n, m, edges);
   return 0;
}

Eingabe

5, 6, {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}

Ausgabe

4

Das obige ist der detaillierte Inhalt vonC++-Programm zum Ermitteln der maximalen Bewertungskomponente, die aus einem Diagramm reduziert werden kann. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!