 Backend-Entwicklung
Backend-Entwicklung
 C++
C++
 C++-Programm zum Ermitteln der Mindestpunktzahl, die zum Erreichen einer G-Punktzahl erforderlich ist
C++-Programm zum Ermitteln der Mindestpunktzahl, die zum Erreichen einer G-Punktzahl erforderlich ist
C++-Programm zum Ermitteln der Mindestpunktzahl, die zum Erreichen einer G-Punktzahl erforderlich ist

Angenommen, wir haben zwei Arrays p und c, jedes Array hat D Elemente und es gibt eine weitere Zahl G. Bedenken Sie, dass bei einem Programmierwettbewerb jede Frage anhand ihres Schwierigkeitsgrads bewertet wird. Die Punktzahl der Frage p[i] beträgt 100i. Diese p[1] + ... + p[D]-Probleme sind allesamt Probleme im Wettbewerb. Benutzer auf Programmierwebsites haben einen numerischen Gesamtscore. Der total_score des Benutzers ist die Summe der folgenden zwei Elemente.
Grundpunktzahl: Die Summe der Punktzahlen aller gelösten Probleme
Belohnung: Wenn der Benutzer alle Probleme mit einer Punktzahl von 100i löst, wird zusätzlich zur Basispunktzahl eine perfekte Belohnung c[ i] wird erhalten.
Amal ist neu im Wettbewerb und hat noch keine Probleme gelöst. Sein Ziel ist es, eine Gesamtnote von G oder mehr zu erreichen. Wir müssen herausfinden, wie viele Probleme er mindestens lösen muss, um dieses Ziel zu erreichen.
Wenn die Eingabe also G = 500; P = [3, 5]; C = [500, 800] ist, beträgt die Ausgabe 3
Schritte
Um dieses Problem zu lösen, befolgen wir die folgenden Schritte:
Beispiel
Sehen wir uns zum besseren Verständnis die Implementierung unten an: -
D := size of p
mi := 10000
for initialize i := 0, when i < 1 << D, update (increase i by 1), do:
sum := 0
count := 0
at := 0
an array to store 10 bits b, initialize from bit value of i
for initialize j := 0, when j < D, update (increase j by 1), do:
if jth bit in b is 1, then:
count := p[j]
sum := sum + ((j + 1) * 100 * p[j] + c[j]
Otherwise
at := j
if sum < G, then:
d := (G - sum + (at + 1) * 100 - 1) / ((at + 1) * 100)
if d <= p[at], then:
sum := sum + (at + 1)
count := count + d
if sum >= G, then:
mi := minimum of mi and count
return miInput
#include <bits/stdc++.h>
using namespace std;
int solve(int G, vector<int> p, vector<int> c){
int D = p.size();
int mi = 10000;
for (int i = 0; i < 1 << D; i++){
int sum = 0;
int count = 0;
int at = 0;
bitset<10> b(i);
for (int j = 0; j < D; j++){
if (b.test(j)){
count += p.at(j);
sum += (j + 1) * 100 * p.at(j) + c.at(j);
} else {
at = j;
}
}
if (sum < G){
int d = (G - sum + (at + 1) * 100 - 1) / ((at + 1) * 100);
if (d <= p.at(at)){
sum += (at + 1) * 100 * d;
count += d;
}
}
if (sum >= G) {
mi = min(mi, count);
}
}
return mi;
}
int main() {
int G = 500;
vector<int> P = { 3, 5 };
vector<int> C = { 500, 800 };
cout << solve(G, P, C) << endl;
}Output
500, { 3, 5 }, { 500, 800 }Das obige ist der detaillierte Inhalt vonC++-Programm zum Ermitteln der Mindestpunktzahl, die zum Erreichen einer G-Punktzahl erforderlich ist. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Übersetzen Sie Folgendes ins Chinesische: C-Programm zur Konvertierung römischer Ziffern in Dezimalzahlen
Sep 05, 2023 pm 09:53 PM
Übersetzen Sie Folgendes ins Chinesische: C-Programm zur Konvertierung römischer Ziffern in Dezimalzahlen
Sep 05, 2023 pm 09:53 PM
Nachfolgend finden Sie einen C-Sprachalgorithmus zum Konvertieren römischer Ziffern in Dezimalzahlen: Algorithmus Schritt 1 – Start Schritt 2 – Römische Ziffern zur Laufzeit lesen Schritt 3 – Länge: = strlen(roman) Schritt 4 – Für i=0 bis Länge-1 Schritt 4.1-switch(roman[i]) Schritt 4.1.1-case'm': &nbs
 C++-Programm zum Vergleich der lexikografischen Reihenfolge zweier Zeichenfolgen
Sep 04, 2023 pm 05:13 PM
C++-Programm zum Vergleich der lexikografischen Reihenfolge zweier Zeichenfolgen
Sep 04, 2023 pm 05:13 PM
Der lexikografische Zeichenfolgenvergleich bedeutet, dass Zeichenfolgen in Wörterbuchreihenfolge verglichen werden. Wenn beispielsweise zwei Zeichenfolgen „apple“ und „appeal“ vorhanden sind, steht die erste Zeichenfolge an letzter Stelle, da die ersten drei Zeichen von „app“ identisch sind. Dann ist das Zeichen für die erste Zeichenfolge „l“ und in der zweiten Zeichenfolge ist das vierte Zeichen „e“. Da „e“ kürzer als „l“ ist, steht es an erster Stelle, wenn wir lexikografisch sortieren. Zeichenfolgen werden vor der Anordnung lexikografisch verglichen. In diesem Artikel werden wir verschiedene Techniken zum lexikografischen Vergleich zweier Zeichenfolgen mit C++ kennenlernen. Verwendung der Funktion „compare()“ in C++-Strings Das C++-String-Objekt verfügt über eine Funktion „compare()“
 So berechnen Sie die Bewertung des Hauses in Misty Jianghu
Feb 29, 2024 pm 12:43 PM
So berechnen Sie die Bewertung des Hauses in Misty Jianghu
Feb 29, 2024 pm 12:43 PM
In Yanyu Jianghu gibt es eine Art Haus-Gameplay. Nachdem das Haus erfolgreich gebaut wurde, erhält der Spieler auch eine eigene Hauspunktzahl Die Berechnungsmethode lautet natürlich auch. Sie wird mit der angegebenen Berechnungsmethode berechnet, und die Spieler können einen Blick darauf werfen. Berechnungsmethode für die Hauspunktzahl in Yanyujianghu 1. Hauspunktzahl: Aussehenspunktzahl, Platzierungspunktzahl, Skalenpunktzahl und Forschung sind in vier Teile unterteilt. 2. Aussehenspunktzahl: hauptsächlich Gebäudehautbonuspunkte und Bewegungsbonuspunkte (200 Punkte). Es gibt zwei Arten von Gebäudehäuten: Die eine ist der Handflicken, der oben im Baumarkt ausgetauscht wird, und der andere ist der Hautflicken auf dem Drehteller. 3. Platzierungspunkte: Die durch die hergestellten Möbel erzielten Punkte, die grüne Obergrenze 10 Punkte, die blaue Obergrenze beträgt 15 Punkte und die violette Obergrenze beträgt 10 Punkte.
 So fügen Sie Brüche in Word ein
Mar 19, 2024 pm 08:31 PM
So fügen Sie Brüche in Word ein
Mar 19, 2024 pm 08:31 PM
Es mag viele Leute geben, die nicht wissen, wie man Brüche in Word einfügt. Schließlich kommt die Situation, Brüche einzugeben, nicht oft vor. Wenn Sie jedoch darauf stoßen, wird es problematischer, daher sollten wir wissen, wie man Word-Partituren eingibt. Die Eingabe von Brüchen in Word ist eigentlich sehr einfach. Als Nächstes erkläre ich, wie man Brüche in Word eingibt. Es gibt viele Möglichkeiten, Brüche in Word einzugeben. Eine davon ist die Verwendung der Funktion „Formel einfügen“. Die Schritte sind wie folgt: Nachdem Sie das Word-Dokument geöffnet haben, klicken Sie in der Menüleiste auf die Option [Einfügen] und wählen Sie dann im Popup-Menü die Option [Formel] aus. Dadurch wird ein Formeleditor geöffnet, in den Sie den gewünschten Bruch eingeben können. Im Editor können Sie die Bruchformatschaltflächen zum Erstellen von Brüchen verwenden oder manuell „\frac{numerator}{“ eingeben.
 C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird
Sep 17, 2023 am 10:49 AM
C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird
Sep 17, 2023 am 10:49 AM
Hyperbelfunktionen werden mithilfe von Hyperbeln anstelle von Kreisen definiert und entsprechen gewöhnlichen trigonometrischen Funktionen. Es gibt den Verhältnisparameter in der hyperbolischen Sinusfunktion aus dem angegebenen Winkel im Bogenmaß zurück. Aber machen Sie das Gegenteil, oder anders gesagt. Wenn wir einen Winkel aus einem hyperbolischen Sinus berechnen wollen, benötigen wir eine umgekehrte hyperbolische trigonometrische Operation wie die hyperbolische Umkehrsinusoperation. In diesem Kurs wird gezeigt, wie Sie die hyperbolische Umkehrsinusfunktion (asinh) in C++ verwenden, um Winkel mithilfe des hyperbolischen Sinuswerts im Bogenmaß zu berechnen. Die hyperbolische Arkussinusoperation folgt der folgenden Formel -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Wo\:In\:ist\:natürlicher Logarithmus\:(log_e\:k)
 C-Programm zum Ermitteln der Länge einer verknüpften Liste
Sep 07, 2023 pm 07:33 PM
C-Programm zum Ermitteln der Länge einer verknüpften Liste
Sep 07, 2023 pm 07:33 PM
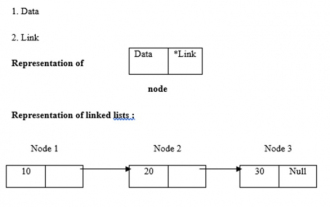
Verknüpfte Listen verwenden eine dynamische Speicherzuweisung, d. h. sie wachsen und schrumpfen entsprechend. Sie werden als Ansammlungen von Knoten definiert. Hier besteht ein Knoten aus zwei Teilen: Daten und Links. Die Darstellung von Daten, Links und verknüpften Listen ist wie folgt: - Arten von verknüpften Listen Es gibt vier Arten von verknüpften Listen: - Einfach verknüpfte Liste / Einfach verknüpfte Liste Doppelt / Doppelt verknüpfte Liste Zirkuläre einfach verknüpfte Liste Zirkuläre doppelt verknüpfte Liste Wir Verwenden Sie die rekursive Methode, um die Länge der verknüpften Liste zu ermitteln. Die Logik lautet -intlength(node *temp){ if(temp==NULL) returnl;
 C++-Programm zum Drucken eines Wörterbuchs
Sep 11, 2023 am 10:33 AM
C++-Programm zum Drucken eines Wörterbuchs
Sep 11, 2023 am 10:33 AM
Eine Karte ist ein spezieller Containertyp in C++, bei dem jedes Element ein Paar aus zwei Werten ist, nämlich einem Schlüsselwert und einem zugeordneten Wert. Der Schlüsselwert wird zum Indizieren jedes Elements verwendet, und der zugeordnete Wert ist der mit dem Schlüssel verknüpfte Wert. Unabhängig davon, ob der zugeordnete Wert eindeutig ist, ist der Schlüssel immer eindeutig. Um Kartenelemente in C++ zu drucken, müssen wir einen Iterator verwenden. Ein Element in einer Menge von Elementen wird durch ein Iteratorobjekt angegeben. Iteratoren werden hauptsächlich mit Arrays und anderen Arten von Containern (z. B. Vektoren) verwendet und verfügen über einen bestimmten Satz von Operationen, mit denen bestimmte Elemente innerhalb eines bestimmten Bereichs identifiziert werden können. Iteratoren können inkrementiert oder dekrementiert werden, um auf verschiedene Elemente in einem Bereich oder Container zu verweisen. Der Iterator zeigt auf den Speicherort eines bestimmten Elements im Bereich. Drucken einer Karte in C++ mit Iteratoren Schauen wir uns zunächst an, wie man definiert
 Das C-Programm verwendet die Funktion rename(), um den Dateinamen zu ändern
Sep 21, 2023 pm 10:01 PM
Das C-Programm verwendet die Funktion rename(), um den Dateinamen zu ändern
Sep 21, 2023 pm 10:01 PM
Die Umbenennungsfunktion ändert den alten Namen einer Datei oder eines Verzeichnisses in den neuen Namen. Dieser Vorgang ähnelt dem Verschiebevorgang. Wir können diese Umbenennungsfunktion also auch zum Verschieben von Dateien verwenden. Diese Funktion ist in der Headerdatei der stdio.h-Bibliothek vorhanden. Die Syntax der Umbenennungsfunktion lautet wie folgt: intrename(constchar*oldname,constchar*newname); Die Funktion der rename()-Funktion akzeptiert zwei Parameter. Einer ist alter Name und der andere ist neuer Name. Beide Parameter sind Zeiger auf konstante Zeichen, die den alten und neuen Namen der Datei definieren. Gibt Null zurück, wenn die Datei erfolgreich umbenannt wurde; andernfalls wird eine Ganzzahl ungleich Null zurückgegeben. Während eines Umbenennungsvorgangs



