
Gradientenabstieg ist eine wichtige Optimierungsmethode beim maschinellen Lernen, die verwendet wird, um die Verlustfunktion des Modells zu minimieren. Für den Laien bedeutet dies, dass die Parameter des Modells wiederholt geändert werden müssen, bis der ideale Wertebereich gefunden ist, der die Verlustfunktion minimiert. Die Methode funktioniert, indem sie winzige Schritte in Richtung des negativen Gradienten der Verlustfunktion durchführt, oder genauer gesagt, entlang des Pfads des steilsten Abfalls. Die Lernrate ist ein Hyperparameter, der den Kompromiss zwischen Geschwindigkeit und Genauigkeit des Algorithmus regelt und die Größe der Schrittweite beeinflusst. Viele Methoden des maschinellen Lernens, darunter lineare Regression, logistische Regression und neuronale Netze, um nur einige zu nennen, nutzen den Gradientenabstieg. Seine Hauptanwendung ist das Modelltraining, bei dem das Ziel darin besteht, die Differenz zwischen dem erwarteten und dem tatsächlichen Wert der Zielvariablen zu minimieren. In diesem Artikel werden wir uns mit der Implementierung des Gradientenabstiegs in Python befassen, um lokale Minima zu finden.
Jetzt ist es an der Zeit, den Gradientenabstieg in Python zu implementieren. Hier ist eine grundlegende Erklärung, wie wir es umsetzen –
Zuerst importieren wir die notwendigen Bibliotheken.
Definieren Sie seine Funktion und seine Ableitungen.
Als nächstes wenden wir die Gradientenabstiegsfunktion an.
Nachdem wir die Funktion angewendet haben, legen wir die Parameter fest, um das lokale Minimum zu finden,
Abschließend werden wir die Ausgabe grafisch darstellen.
Bibliothek importieren
import numpy as np import matplotlib.pyplot as plt
Dann definieren wir die Funktion f(x) und ihre Ableitung f'(x) -
def f(x): return x**2 - 4*x + 6 def df(x): return 2*x - 4
F(x) ist die Funktion, die reduziert werden muss und df ist ihre Ableitung (x). Die Gradientenabstiegsmethode verwendet Ableitungen, um sich zum Minimum zu führen, indem sie die Steigung der Funktion auf dem Weg offenlegt.
Dann definieren Sie die Gradientenabstiegsfunktion.
def gradient_descent(initial_x, learning_rate, num_iterations):
x = initial_x
x_history = [x]
for i in range(num_iterations):
gradient = df(x)
x = x - learning_rate * gradient
x_history.append(x)
return x, x_history
x, die Lernrate und die erforderliche Anzahl von Iterationen werden an die Gradientenabstiegsfunktion gesendet. Um den Wert von x nach jeder Iteration zu speichern, wird x auf seinen ursprünglichen Wert initialisiert und eine leere Liste generiert. Die Methode führt dann einen Gradientenabstieg für die angegebene Anzahl von Iterationen durch und ändert x in jeder Iteration gemäß der Gleichung x = x – Lernrate * Gradient. Diese Funktion generiert eine Liste von x-Werten für jede Iteration und den Endwert von x.
Die Gradientenabstiegsfunktion kann jetzt verwendet werden, um das lokale Minimum von f(x) zu lokalisieren –
initial_x = 0
learning_rate = 0.1
num_iterations = 50
x, x_history = gradient_descent(initial_x, learning_rate, num_iterations)
print("Local minimum: {:.2f}".format(x))
Local minimum: 2.00
In dieser Abbildung ist x zunächst auf 0 gesetzt, die Lernrate beträgt 0,1 und es werden 50 Iterationen ausgeführt. Abschließend veröffentlichen wir den Wert von x, der nahe am lokalen Minimum bei x=2 liegen sollte.
Durch die grafische Darstellung der Funktion f(x) und des x-Werts für jede Iteration können wir den Gradientenabstiegsprozess in Aktion sehen –
# Create a range of x values to plot
x_vals = np.linspace(-1, 5, 100)
# Plot the function f(x)
plt.plot(x_vals, f(x_vals))
# Plot the values of x at each iteration
plt.plot(x_history, f(np.array(x_history)), 'rx')
# Label the axes and add a title
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradient Descent')
# Show the plot
plt.show()
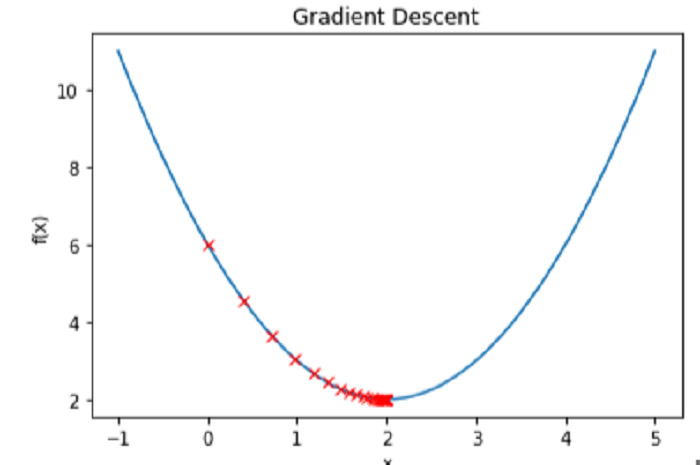
Zusammenfassend lässt sich sagen, dass Python zum Ermitteln des lokalen Minimums einer Funktion einen effizienten Optimierungsprozess namens Gradientenabstieg verwendet. Beim Gradientenabstieg wird bei jedem Schritt die Ableitung einer Funktion berechnet und die Eingabewerte wiederholt in Richtung des steilsten Abfalls aktualisiert, bis der niedrigste Wert erreicht ist. Die Implementierung des Gradientenabstiegs in Python erfordert die Angabe der zu optimierenden Funktion und ihrer Ableitungen, die Initialisierung von Eingabewerten sowie die Bestimmung der Lernrate und Anzahl der Iterationen des Algorithmus. Nachdem die Optimierung abgeschlossen ist, kann die Methode evaluiert werden, indem ihre Schritte auf das Minimum zurückgeführt werden und beobachtet wird, wie sie dieses Ziel erreicht. Der Gradientenabstieg ist eine nützliche Technik für maschinelles Lernen und Optimierungsanwendungen, da Python große Datenmengen und komplexe Funktionen verarbeiten kann.
Das obige ist der detaillierte Inhalt vonWie implementiert man einen Gradientenabstiegsalgorithmus in Python, um lokale Minima zu finden?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




