zentrale Zwölfeckzahl

Die grafischen Zahlen, die ein Zwölfeck darstellen, werden Zwölfeckzahlen genannt. Die zentrale Zwölfeckzahl wird durch einen Punkt in der Mitte und andere diesen Punkt umgebende Punkte in einer Schicht aus fortlaufenden Zwölfecken (d. h. 12-seitigen Polygonen) dargestellt.

Die zentrale Zwölfeckzahl lässt sich anhand des Bildes unten besser erklären.

Für n=1 gibt es nur einen Punkt in der Mitte. Die Ausgabe ist also 1.

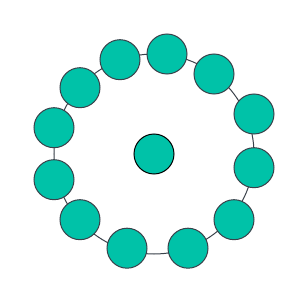
Für n=2 gibt es einen Punkt in der Mitte, der von einem Zwölfeck umgeben ist. Die Gesamtpunktzahl beträgt somit 13. Die nächste zentrale Zwölfeckzahl wird also 13 sein.

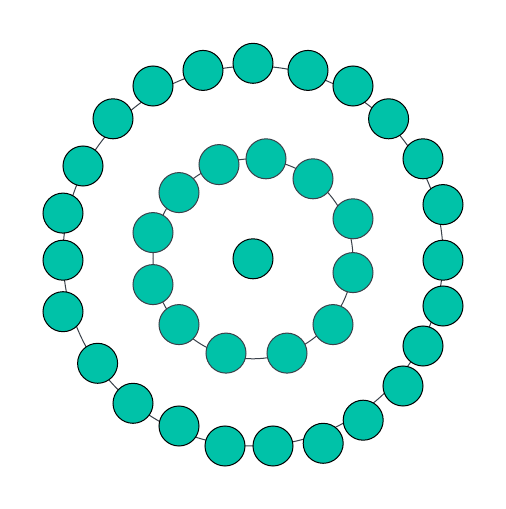
Für n=3 gibt es einen einzelnen Punkt in der Mitte, gefolgt von einem ihn umgebenden Zwölfeck und dann der nächsten aufeinanderfolgenden Schicht von Zwölfecken mit 24 Punkten. Daher beträgt die Gesamtpunktzahl 37, was der nächsten zentralen Zwölfeckzahl entspricht.

Ebenso gilt dies für jede positive Zahl n. In diesem Zusammenhang lauten die ersten Zwölfeckzahlen 1, 13, 37, 73, 121, 181…..

In diesem Problem erhalten wir eine beliebige positive Zahl n und müssen die n-te zentrale Zwölfeckzahl ausgeben.

Zum Beispiel

Geben Sie - 2

ein

Ausgabe - 13

Geben Sie - 5

ein

Ausgabe - 121

Hier ist der Algorithmus zur Lösung dieses Problems.

Algorithmus

Um die n-te zentrale Zwölfeckzahl zu berechnen, müssen wir das in der Aufgabe verfolgte Muster herausfinden.

Nach dem Konzept der zentralen Zwölfeckzahl wird sie durch einen Punkt in der Mitte und dann aufeinanderfolgende Schichten von Zwölfecken dargestellt. Die aufeinanderfolgenden zwölfeckigen Schichten sind 12, 24, 36, 48 ... Wenn wir uns das Muster genau ansehen, bildet es eine arithmetische Folge mit einer Toleranz von 12.

Da die ersten paar Folgen zentraler Zwölfeckzahlen 1, 13, 37, 73… sind. Es ist nichts weiter als die Summe der Zwölfeckschichten und eines Punktes in der Mitte.

Wir können es besser verstehen, wenn wir eine Folge aufeinanderfolgender zwölfeckiger Schichten betrachten, die mit 0 beginnen.

0, 12, 24, 36, 48.
For n=1, the centred dodecagonal number is 1 which is 0+1.
For n=2, the centred dodecagonal number is 13 which is 0+12+1.
For n=3, the centred dodecagonal number is 37 which is 0+12+24+1.

Von hier aus können wir denken, dass die n-te zentrale Zwölfeckzahl nichts anderes ist als die Summe von A.P. von n Termen beginnend bei 0 mit einer Toleranz von 12 und 1.

Die Formel der n-ten zentralen Zwölfeckzahl kann also ausgedrückt werden als:

$$mathrm{CDn=arithmetische Folge (a=0: Summe: d=12): von: Summe der ersten n Terme: +1}$$

$$mathrm{CD_n:=:frac{n}{2}(2a:+:(n-1)d):+1}$$

Hier ist $mathrm{CD_n}$ die n-te zentrale Zwölfeckzahl

a ist der erste Term der arithmetischen Folge, der 0

ist

d ist die Toleranz der arithmetischen Folge, die 12

beträgt

Ferner kann die Formel wie folgt geschrieben werden:

$$mathrm{CD_n:=:frac{12n}{2}(n-1):+:1}$$

$$mathrm{CD_n:=:6n(n-1):+:1}$$

Behalten Sie den Originaltext ohne Übersetzung

Wir werden die obige Formel verwenden, um die n-te zentrale Zwölfeckzahl in unserer Methode zu berechnen.

Methode

• Um dieses Problem zu lösen, erstellen wir einfach eine Funktion zur Berechnung der n-ten zentralen Zwölfeckzahl.

• Wir werden die oben abgeleitete Formel verwenden, um die n-te zentrale Zwölfeckzahl für alle n positiven Zahlen zu berechnen.

• Gibt den berechneten Wert zurück, der unsere gewünschte Ausgabe sein wird.

Die chinesische Übersetzung von

Beispiel

lautet:

Beispiel

Das Folgende ist die Implementierung der obigen Methode in C++ -

#include <iostream>
#include<bits/stdc++.h>

using namespace std;

//function to calculate the nth centred dodecagonal number
int CDn(int N){
   int ans= 6 * N * (N-1) + 1; //used to store nth centred dodecagonal number value
   
   return ans; //return the answer
}
int main(){
   int N=8;
   cout<<CDn(N)<<endl;
   
   N=6;
   cout<<CDn(N)<<endl;
   
   N=12;
   cout<<CDn(N)<<endl;
   
   return 0;
}

Ausgabe

337
181
793

Zeitkomplexität: O(1), da konstante Zeit erforderlich ist.

Raumkomplexität: O(1), da wir keinen zusätzlichen Platz beanspruchen.

Fazit

In diesem Artikel haben wir das Problem gelöst, die n-te zentrierte Zwölfeckzahl zu drucken. Wir haben das Konzept der zentrierten Zwölfeckzahlen gelernt und die Formel für die n-te Zahl abgeleitet,

Ich hoffe, dass Ihnen dieser Artikel dabei geholfen hat, alle Konzepte zu diesem Thema zu verstehen und zu klären.

Das obige ist der detaillierte Inhalt vonzentrale Zwölfeckzahl. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!