 Backend-Entwicklung
Backend-Entwicklung
 C++
C++
 Fügen Sie jedem Knoten alle größeren Werte im angegebenen binären Suchbaum hinzu
Fügen Sie jedem Knoten alle größeren Werte im angegebenen binären Suchbaum hinzu
Fügen Sie jedem Knoten alle größeren Werte im angegebenen binären Suchbaum hinzu

BST oder Binary Search Tree ist eine Form eines Binärbaums, in dem alle linken Knoten Werte haben, die kleiner als der Wert des Wurzelknotens sind, und alle rechten Knoten Werte haben, die größer als der Wert des Wurzelknotens sind. Für dieses Problem nehmen wir einen Binärbaum und fügen ihm alle Werte hinzu, die größer als der aktuelle Knotenwert sind. Das Problem „Füge alle größeren Werte zu jedem Knoten eines BST hinzu“ wird vereinfacht, indem für einen BST alle Knotenwerte, die größer als der aktuelle Knotenwert sind, zu diesem Knotenwert addiert werden.
Fügen Sie alle Knoten mit größerem Wert zu jedem Knoten in der BST-Problemstellung hinzu:
Bei einem binären Suchbaum (BST) müssen wir für jeden Knoten die Summe aller Knoten mit größerem Wert addieren.
Eingabe
10
/ \
/ \
5 20
/ \ / \
1 7 1 5Ausgabe
70
/ \
82 45
/ \ / \
83 77 60 25Erläuterung
Dieses Programm wandelt einen binären Suchbaum in einen binären Baum um, in dem der Wert eines Knotens die Summe aller größeren Elemente plus dem ursprünglichen Wert des Knotens ist.
Fügen Sie alle größeren Werte zu jedem Knoten in der binären Suchbaumlösung hinzu:
Wir verwenden die umgekehrte Inorder-Traversierung (rufen rekursiv zuerst den rechten Teilbaum anstelle des linken Teilbaums auf) und verwalten eine Variable zum Speichern der Summe der Knoten wurden bisher durchquert.
Wir verwenden diese Summe dann, um den Wert des aktuellen Knotens zu ändern, indem wir zunächst seinen Wert zur Summe addieren und dann den Wert des Knotens durch diese Summe ersetzen.
Beispiel
#include <iostream >
using namespace std;
struct node {
int data;
node *left;
node *right;
};
node *newNode(int key) {
node *temp=new node;
temp->left=NULL;
temp->right=NULL;
temp->data=key;
return temp;
}
void Inorder(node *root) {
if(!root)
return;
Inorder(root->left);
cout<<root->data<<" ";
Inorder(root->right);
}
node *Insert(node *root,int key) {
if(!root)
return newNode(key);
if(key<root->data)
root->left=Insert(root->left,key);
else
root->right=Insert(root->right,key);
return root;
}
void RevInorderAdd(node *root,int &sum) {
if(!root)
return;
RevInorderAdd(root->right,sum);
sum+=root->data;
root->data=sum;
RevInorderAdd(root->left,sum);
}
void AddGreater(node *root) {
int sum=0;
RevInorderAdd(root,sum);
}
int main() {
/* Let us create following BST
10
/ \
5 20
/ \ / \
1 7 15 25 */
node *root = NULL;
root = Insert(root, 10);
Insert(root, 20);
Insert(root, 25);
Insert(root, 15);
Insert(root, 5);
Insert(root, 7);
Insert(root, 1);
Inorder(root);
cout<<endl;
AddGreater(root);
Inorder(root);
cout<<endl;
return 0;
}Das obige ist der detaillierte Inhalt vonFügen Sie jedem Knoten alle größeren Werte im angegebenen binären Suchbaum hinzu. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Fragen Sie das Mindestgewicht im Teilbaum ab Knoten X und höchstens Abstand D ab
Aug 25, 2023 am 11:25 AM
Fragen Sie das Mindestgewicht im Teilbaum ab Knoten X und höchstens Abstand D ab
Aug 25, 2023 am 11:25 AM
Bei der Computerprogrammierung ist es manchmal erforderlich, das Mindestgewicht eines Teilbaums zu ermitteln, der von einem bestimmten Knoten stammt, vorausgesetzt, der Teilbaum darf keine Knoten enthalten, die mehr als D Einheiten vom angegebenen Knoten entfernt sind. Dieses Problem tritt in verschiedenen Bereichen und Anwendungen auf, darunter in der Graphentheorie, baumbasierten Algorithmen und der Netzwerkoptimierung. Ein Teilbaum ist eine Teilmenge einer größeren Baumstruktur, wobei der angegebene Knoten als Wurzelknoten des Teilbaums dient. Ein Teilbaum enthält alle Nachkommen des Wurzelknotens und deren Verbindungskanten. Die Gewichtung eines Knotens bezieht sich auf einen bestimmten, diesem Knoten zugewiesenen Wert, der seine Wichtigkeit, Wichtigkeit oder andere relevante Metriken darstellen kann. Bei diesem Problem besteht das Ziel darin, das Mindestgewicht aller Knoten in einem Teilbaum zu ermitteln und gleichzeitig den Teilbaum auf Knoten zu beschränken, die höchstens D Einheiten vom Wurzelknoten entfernt sind. Im folgenden Artikel werden wir uns mit der Komplexität des Minings von Mindestgewichten aus Teilbäumen befassen
 C++-Code zum Umkehren von Pfaden in einem binären Suchbaum mithilfe von Warteschlangen
Sep 14, 2023 pm 07:21 PM
C++-Code zum Umkehren von Pfaden in einem binären Suchbaum mithilfe von Warteschlangen
Sep 14, 2023 pm 07:21 PM
Bei einem gegebenen binären Suchbaum müssen wir beispielsweise seinen Pfad von einem bestimmten Schlüssel aus umkehren. Möglichkeiten, die Lösung zu finden Bei diesem Ansatz erstellen wir eine Warteschlange und pushen alle Knoten, bis wir den Wurzelknoten erhalten. p>Beispiel #include<bits/stdc++.h>usingnamespacestd;structnode{ intkey; structnode*left,*right;};structnode*newNode(initem){&nb
 Wie implementiert man die Funktionen zum Kopieren und Ausschneiden von Knoten von Mind Maps über Vue und jsmind?
Aug 15, 2023 pm 05:57 PM
Wie implementiert man die Funktionen zum Kopieren und Ausschneiden von Knoten von Mind Maps über Vue und jsmind?
Aug 15, 2023 pm 05:57 PM
Wie implementiert man die Funktionen zum Kopieren und Ausschneiden von Knoten von Mind Maps über Vue und jsmind? Mindmap ist ein gängiges Denkwerkzeug, das uns helfen kann, unsere Gedanken zu ordnen und unsere Denklogik zu ordnen. Die Funktionen zum Kopieren und Ausschneiden von Knoten sind häufig verwendete Vorgänge in Mind Maps, mit denen wir vorhandene Knoten bequemer wiederverwenden und die Effizienz der Denkorganisation verbessern können. In diesem Artikel werden wir die beiden Tools Vue und jsmind verwenden, um die Funktionen zum Kopieren und Ausschneiden von Knoten der Mind Map zu implementieren. Zuerst müssen wir Vue und jsmind installieren und erstellen
 So implementieren Sie einen binären Suchbaum in Python
Jun 10, 2023 am 08:57 AM
So implementieren Sie einen binären Suchbaum in Python
Jun 10, 2023 am 08:57 AM
Binary Search Tree (BST) ist ein Suchalgorithmus, der auf Binärbäumen basiert. Sein Merkmal besteht darin, dass der Wert im linken Teilbaum jedes Knotens im Baum kleiner ist als der Wert dieses Knotens, während der Wert im rechten Teilbaum größer als der Wert dieses Knotens ist. Daher beträgt die zeitliche Komplexität von BST-Such- und Einfügungsoperationen O(logN). Die Methode zum Implementieren eines binären Suchbaums in Python ist relativ einfach, da Python über zwei integrierte Datenstrukturen, Listen und Wörterbücher, verfügt, die beide zum Implementieren von Binärbäumen verwendet werden können. Hier
 Binärer Heap und binärer Suchbaum in C++
Aug 22, 2023 pm 04:10 PM
Binärer Heap und binärer Suchbaum in C++
Aug 22, 2023 pm 04:10 PM
In der C++-Programmierung sind binärer Heap und binärer Suchbaum zwei häufig verwendete Datenstrukturen. Sie weisen Ähnlichkeiten, aber auch Unterschiede auf. In diesem Artikel werden die Konzepte, Grundoperationen und Anwendungsszenarien von binären Heaps bzw. binären Suchbäumen vorgestellt. 1. Binärer Heap 1.1 Konzept Der binäre Heap ist ein vollständiger Binärbaum, der die folgenden zwei Eigenschaften erfüllt: 1.1.1 Heap-Reihenfolge Heap-Reihenfolge bedeutet, dass in einem binären Heap der Wert jedes Knotens nicht größer (oder nicht kleiner als) ist Wert seines übergeordneten Knotens. Hier nehmen wir als Beispiel den maximalen Heap, dh der Wert des Wurzelknotens ist der größte Wert im gesamten Baum
 Was ist die Methode zum Löschen eines Knotens in js?
Sep 01, 2023 pm 05:00 PM
Was ist die Methode zum Löschen eines Knotens in js?
Sep 01, 2023 pm 05:00 PM
Die Methoden zum Löschen von Knoten in js sind: 1. Die Methode „removeChild()“ wird verwendet, um den angegebenen untergeordneten Knoten vom übergeordneten Knoten zu entfernen. Der erste Parameter ist der zu löschende untergeordnete Knoten der übergeordnete Knoten. 2. Die Methode parentNode.removeChild() kann direkt über den übergeordneten Knoten aufgerufen werden. 3. Die Methode „remove()“ kann den Knoten direkt löschen Das innerHTML-Attribut wird zum Löschen des Knotens verwendet.
 Finden Sie mit dem Floyd-Warshal-Algorithmus den kürzesten Weg zwischen zwei beliebigen Knoten
Sep 20, 2023 pm 02:21 PM
Finden Sie mit dem Floyd-Warshal-Algorithmus den kürzesten Weg zwischen zwei beliebigen Knoten
Sep 20, 2023 pm 02:21 PM
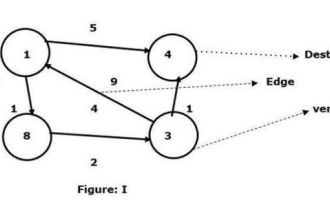
C++ verfügt über ein Makro, das als Codeabschnitt oder erwarteter Wert definiert ist und immer dann wiederverwendet wird, wenn der Benutzer es benötigt. Der Floyd-Walshall-Algorithmus ist der Prozess, den kürzesten Weg zwischen allen Scheitelpunktpaaren in einem gegebenen gewichteten Graphen zu finden. Der Algorithmus folgt einem dynamischen Programmieransatz, um den Minimalgewichtsgraphen zu finden. Lassen Sie uns die Bedeutung des Floyd-Walshall-Algorithmus anhand eines Diagramms verstehen: Nehmen Sie Scheitelpunkt 1 als Quelle und Scheitelpunkt 4 als Ziel und finden Sie den kürzesten Weg zwischen ihnen. Wir haben gesehen, dass es zwei Pfade gibt, die mit dem Zielscheitelpunkt 4 verbunden werden können. 1->4 – die Kante hat ein Gewicht von 51->8->3->4 – das Kantengewicht (1+2+1) ist 4. Im gegebenen Diagramm I sehen wir die kleinste Kante, die zwei Eckpunkte verbindet. Hier also der Scheitelpunkt
 Java verwendet die Funktion max() der Math-Klasse, um die größere von zwei Zahlen zu erhalten
Jul 24, 2023 pm 11:17 PM
Java verwendet die Funktion max() der Math-Klasse, um die größere von zwei Zahlen zu erhalten
Jul 24, 2023 pm 11:17 PM
Java verwendet die Funktion max() der Math-Klasse, um den größeren Wert zweier Zahlen zu ermitteln. Bei der Java-Programmierung müssen wir häufig die Größen zweier Zahlen vergleichen und dann die größere Zahl auswählen, um einige Operationen auszuführen. Die Math-Klasse in Java bietet viele Funktionen für mathematische Operationen, darunter die Funktion max(), die uns dabei helfen kann, den größeren Wert zweier Zahlen zu ermitteln. Die Funktion Math.max() ist wie folgt definiert: publicstaticintmax(inta,intb) Diese Funktion akzeptiert zwei Ganzzahlen



