 Backend-Entwicklung
Backend-Entwicklung
 C++
C++
 Drucken Sie die maximale Summenquadrat-Submatrix einer bestimmten Größe im C-Programm
Drucken Sie die maximale Summenquadrat-Submatrix einer bestimmten Größe im C-Programm
Drucken Sie die maximale Summenquadrat-Submatrix einer bestimmten Größe im C-Programm
Suchen Sie bei einer gegebenen NxN-Matrix eine MxM-Untermatrix mit M=1, so dass die Summe aller Elemente der Matrix MxM maximal ist. Die Eingabe in die Matrix NxN kann Null, positive ganzzahlige und negative ganzzahlige Werte enthalten.
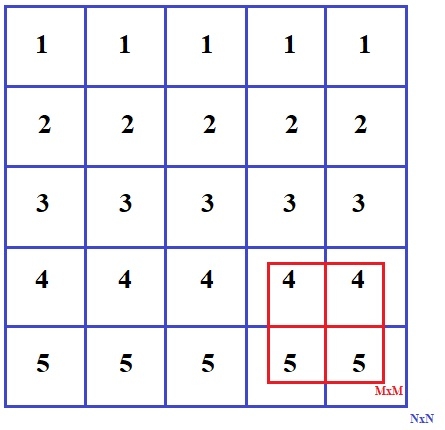
Beispiel
Input:
{{1, 1, 1, 1, 1},
{2, 2, 2, 2, 2},
{3, 3, 3, 3, 3},
{4, 4, 4, 4, 4},
{5, 5, 5, 5, 5} }
Output:
4 4
5 5Das obige Problem kann mit einer einfachen Lösung gelöst werden: Wir können die gesamte Matrix NxN nehmen und dann alle möglichen MxM-Matrizen finden, ihre Summe finden und dann die mit der MxM-Matrix mit der maximalen Summe drucken. Diese Methode ist einfach, erfordert jedoch eine Zeitkomplexität von O(N^2.M^2), daher versuchen wir, eine Methode mit weniger Zeitkomplexität zu finden.
Algorithmus
Start
Step 1 -> Declare Function void matrix(int arr[][size], int k)
IF k>size
Return
Declare int array[size][size]
Loop For int j=0 and j<size and j++
Set sum=0
Loop for int i=0 and i<k and i++
Set sum=sum + arr[i][j]
End
Set array[0][j]=sum
Loop For int i=1 and i<size-k+1 and i++
Set sum=sum+(arr[i+k-1]][j]-arr[i-1][j]
Set arrayi][j]=sum
End
Set int maxsum = INT_MIN and *pos = NULL
Loop For int i=0 and i<size-k+1 and i++)
Set int sum = 0
Loop For int j = 0 and j<k and j++
Set sum += array[i][j]
End
If sum > maxsum
Set maxsum = sum
Set pos = &(arr[i][0])
End
Loop For int j=1 and j<size-k+1 and j++
Set sum += (array[i][j+k-1] - array[i][j-1])
IF sum > maxsum
Set maxsum = sum
Set pos = &(arr[i][j])
End
End
End
Loop For int i=0 and i<k and i++
Loop For int j=0 and j<k and j++
Print *(pos + i*size + j)
End
Print </p><p>
End
Step 2 -> In main()
Declare int array[size][size] = {{1, 1, 1, 1, 1}, {2, 2, 2, 2, 2}, {3, 3, 3, 3, 3}, {4, 4, 4, 4, 4}, {5, 5, 5, 5, 5}}
Declare int k = 2
Call matrix(array, k)
StopBeispiel
#include <bits/stdc++.h>
using namespace std;
#define size 5
void matrix(int arr[][size], int k){
if (k > size) return;
int array[size][size];
for (int j=0; j<size; j++){
int sum = 0;
for (int i=0; i<k; i++)
sum += arr[i][j];
array[0][j] = sum;
for (int i=1; i<size-k+1; i++){
sum += (arr[i+k-1][j] - arr[i-1][j]);
array[i][j] = sum;
}
}
int maxsum = INT_MIN, *pos = NULL;
for (int i=0; i<size-k+1; i++){
int sum = 0;
for (int j = 0; j<k; j++)
sum += array[i][j];
if (sum > maxsum){
maxsum = sum;
pos = &(arr[i][0]);
}
for (int j=1; j<size-k+1; j++){
sum += (array[i][j+k-1] - array[i][j-1]);
if (sum > maxsum){
maxsum = sum;
pos = &(arr[i][j]);
}
}
}
for (int i=0; i<k; i++){
for (int j=0; j<k; j++)
cout << *(pos + i*size + j) << " ";
cout << endl;
}
}
int main(){
int array[size][size] = {
{1, 1, 1, 1, 1},
{2, 2, 2, 2, 2},
{3, 3, 3, 3, 3},
{4, 4, 4, 4, 4},
{5, 5, 5, 5, 5},
};
int k = 2;
matrix(array, k);
return 0;
}Ausgabe
Wenn wir das obige Programm ausführen, generiert es die folgende Ausgabe
4 4 5 5
Das obige ist der detaillierte Inhalt vonDrucken Sie die maximale Summenquadrat-Submatrix einer bestimmten Größe im C-Programm. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 Was soll ich tun, wenn die Rahmenlinie beim Drucken in Excel verschwindet?
Mar 21, 2024 am 09:50 AM
Was soll ich tun, wenn die Rahmenlinie beim Drucken in Excel verschwindet?
Mar 21, 2024 am 09:50 AM
Wenn wir beim Öffnen einer Datei, die gedruckt werden muss, feststellen, dass die Tabellenrahmenlinie aus irgendeinem Grund in der Druckvorschau verschwunden ist, müssen wir uns rechtzeitig darum kümmern, wenn dies auch in Ihrem Ausdruck erscheint file Wenn Sie Fragen wie diese haben, dann schließen Sie sich dem Editor an, um den folgenden Kurs zu erlernen: Was soll ich tun, wenn die Rahmenlinie beim Drucken einer Tabelle in Excel verschwindet? 1. Öffnen Sie eine Datei, die gedruckt werden muss, wie in der Abbildung unten gezeigt. 2. Wählen Sie alle erforderlichen Inhaltsbereiche aus, wie in der Abbildung unten dargestellt. 3. Klicken Sie mit der rechten Maustaste und wählen Sie die Option „Zellen formatieren“, wie in der Abbildung unten gezeigt. 4. Klicken Sie oben im Fenster auf die Option „Rahmen“, wie in der Abbildung unten gezeigt. 5. Wählen Sie links das dünne, durchgezogene Linienmuster im Linienstil aus, wie in der Abbildung unten gezeigt. 6. Wählen Sie „Äußerer Rand“
 Nicht genügend Arbeitsspeicher oder Speicherplatz, um dieses Dokument neu zu formatieren oder zu drucken. Word-Fehler
Feb 19, 2024 pm 07:15 PM
Nicht genügend Arbeitsspeicher oder Speicherplatz, um dieses Dokument neu zu formatieren oder zu drucken. Word-Fehler
Feb 19, 2024 pm 07:15 PM
In diesem Artikel erfahren Sie, wie Sie das Problem lösen können, dass nicht genügend Arbeitsspeicher oder Speicherplatz zum erneuten Seitenieren oder Drucken des Dokuments in Microsoft Word vorhanden ist. Dieser Fehler tritt normalerweise auf, wenn Benutzer versuchen, ein Word-Dokument zu drucken. Wenn ein ähnlicher Fehler auftritt, lesen Sie bitte die Vorschläge in diesem Artikel, um ihn zu beheben. Nicht genügend Arbeitsspeicher oder Speicherplatz, um dieses Dokument erneut zu paginieren oder zu drucken. Word-Fehler. So beheben Sie den Microsoft Word-Druckfehler „Es ist nicht genügend Arbeitsspeicher oder Speicherplatz vorhanden, um das Dokument erneut zu paginieren oder zu drucken.“ Aktualisieren Sie Microsoft Office. Schließen Sie speicherintensive Anwendungen. Ändern Sie Ihren Standarddrucker. Starten Sie Word im abgesicherten Modus. Benennen Sie die Datei „NorMal.dotm“ um. Speichern Sie die Word-Datei als eine andere
 4 Möglichkeiten zum Drucken vom iPhone
Feb 02, 2024 pm 04:10 PM
4 Möglichkeiten zum Drucken vom iPhone
Feb 02, 2024 pm 04:10 PM
In dieser digitalen Welt ist der Bedarf an gedruckten Seiten nicht verschwunden. Während Sie vielleicht denken, dass es bequemer ist, Inhalte auf Ihrem Computer zu speichern und direkt an den Drucker zu senden, können Sie dasselbe auch auf Ihrem iPhone tun. Mit der Kamera Ihres iPhones können Sie ein Foto oder Dokument aufnehmen und die Datei auch direkt speichern, um sie jederzeit auszudrucken. Auf diese Weise können Sie die benötigten Informationen schnell und einfach materialisieren und in einem Papierdokument speichern. Ob bei der Arbeit oder im Alltag, das iPhone bietet Ihnen eine tragbare Drucklösung. Der folgende Beitrag hilft Ihnen dabei, alles zu verstehen, was Sie wissen müssen, wenn Sie Ihr iPhone zum Drucken von Seiten auf einem Drucker verwenden möchten. Drucken vom iPhone: Fragen Sie Apple
 Das Drucken mit dem Snipping-Tool in Windows 11/10 ist nicht möglich
Feb 19, 2024 am 11:39 AM
Das Drucken mit dem Snipping-Tool in Windows 11/10 ist nicht möglich
Feb 19, 2024 am 11:39 AM
Wenn Sie mit dem Snipping Tool in Windows 11/10 nicht drucken können, kann dies an beschädigten Systemdateien oder Treiberproblemen liegen. In diesem Artikel finden Sie Lösungen für dieses Problem. Drucken über Snipping Tool in Windows 11/10 nicht möglich Wenn Sie über Snipping Tool in Windows 11/10 nicht drucken können, verwenden Sie diese Korrekturen: PC-Drucker neu starten Druckwarteschlange löschen Drucker- und Grafiktreiber aktualisieren Snipping Tool reparieren oder zurücksetzen SFC ausführen und DISM Scan verwendet PowerShell-Befehle, um das Snipping Tool zu deinstallieren und neu zu installieren. Lass uns anfangen. 1] Starten Sie Ihren PC und Drucker neu. Ein Neustart Ihres PCs und Druckers hilft, vorübergehende Störungen zu beseitigen
 So unterbrechen Sie den Druckvorgang in Windows 11
Feb 19, 2024 am 11:50 AM
So unterbrechen Sie den Druckvorgang in Windows 11
Feb 19, 2024 am 11:50 AM
Versehentlich eine große Datei gedruckt? Müssen Sie den Druckvorgang stoppen oder pausieren, um Tinte und Papier zu sparen? Es gibt viele Situationen, in denen Sie möglicherweise einen laufenden Druckauftrag auf Ihrem Windows 11-Gerät anhalten müssen. Wie kann ich den Druck unter Windows 11 anhalten? Unter Windows 11 wird durch das Anhalten des Druckvorgangs der Druckauftrag angehalten, die Druckaufgabe wird jedoch nicht abgebrochen. Dies bietet Benutzern eine flexiblere Kontrolle. Dazu gibt es drei Möglichkeiten: Druck über die Taskleiste anhalten Druck über Windows-Einstellungen anhalten Drucken über die Systemsteuerung Schauen wir uns diese nun im Detail an. 1] Drucken über die Taskleiste. Klicken Sie mit der rechten Maustaste auf die Druckwarteschlangenbenachrichtigung in der Taskleiste. Klicken Sie hier, um alle aktiven Druckeroptionen zu öffnen. Klicken Sie hier mit der rechten Maustaste auf den Druckauftrag und wählen Sie „Alle anhalten“.
 Beim Serienbrief von Word wird eine leere Seite gedruckt
Feb 19, 2024 pm 04:51 PM
Beim Serienbrief von Word wird eine leere Seite gedruckt
Feb 19, 2024 pm 04:51 PM
Wenn Sie feststellen, dass beim Drucken eines Seriendruckdokuments mit Word leere Seiten erscheinen, hilft Ihnen dieser Artikel weiter. Serienbrief ist eine praktische Funktion, mit der Sie ganz einfach personalisierte Dokumente erstellen und an mehrere Empfänger senden können. In Microsoft Word genießt die Serienbrieffunktion hohes Ansehen, da sie Benutzern hilft, Zeit zu sparen, indem sie für jeden Empfänger denselben Inhalt manuell kopieren. Um das Serienbriefdokument auszudrucken, können Sie auf die Registerkarte Mailings gehen. Einige Word-Benutzer haben jedoch berichtet, dass der Drucker beim Versuch, ein Serienbriefdokument zu drucken, eine leere Seite druckt oder überhaupt nicht druckt. Dies kann an einer falschen Formatierung oder Druckereinstellungen liegen. Überprüfen Sie die Dokument- und Druckereinstellungen und stellen Sie sicher, dass Sie vor dem Drucken eine Vorschau des Dokuments anzeigen, um sicherzustellen, dass der Inhalt korrekt ist. Wenn
 So drucken Sie alle Anhänge in Outlook
Feb 20, 2024 am 10:30 AM
So drucken Sie alle Anhänge in Outlook
Feb 20, 2024 am 10:30 AM
Outlook ist einer der funktionsreichsten E-Mail-Clients und zu einem unverzichtbaren Werkzeug für die professionelle Kommunikation geworden. Eine der Herausforderungen besteht darin, alle Anhänge gleichzeitig in Outlook zu drucken. Normalerweise müssen Sie Anhänge einzeln herunterladen, bevor Sie sie drucken können. Wenn Sie jedoch alles auf einmal drucken möchten, ist dies das Problem, mit dem die meisten Menschen konfrontiert sind. So drucken Sie alle Anhänge in Outlook Obwohl die meisten Informationen online in der Outlook-Anwendung verwaltet werden, kann es vorkommen, dass Sie die Informationen zur Sicherung ausdrucken müssen. Sie müssen Dokumente persönlich unterzeichnen, um rechtliche Anforderungen wie Verträge, behördliche Formulare oder Hausaufgaben zu erfüllen. Es gibt mehrere Methoden, mit denen Sie alle Anhänge in Outlook mit einem Klick drucken können, anstatt sie einzeln zu drucken. Schauen wir uns jeden einzelnen im Detail an. Outloo
 So implementieren Sie die Druckfunktion in Vue
Nov 07, 2023 pm 12:33 PM
So implementieren Sie die Druckfunktion in Vue
Nov 07, 2023 pm 12:33 PM
Für die Implementierung der Druckfunktionalität in Vue sind bestimmte Codebeispiele erforderlich. Vue.js ist ein progressives JavaScript-Framework zum Erstellen von Benutzeroberflächen. In vielen Webanwendungen ist die Druckfunktionalität ein sehr wichtiger Bestandteil. In diesem Artikel wird die Implementierung der Druckfunktion in Vue vorgestellt und spezifische Codebeispiele bereitgestellt. Um die Druckfunktion in Vue zu implementieren, müssen Sie zunächst klären, um welchen gedruckten Inhalt es sich handelt. Normalerweise fügen wir den zu druckenden Inhalt in ein HTML-Element ein, beispielsweise ein div. Dann über Jav



