Berechnen Sie bei einem gegebenen azyklischen Graphen die minimale Summe der Elemente in jeder Tiefe

Ein Graph, der keine Zyklen oder Schleifen enthält, wird als azyklischer Graph bezeichnet. Ein Baum ist ein azyklischer Graph, in dem jeder Knoten mit einem anderen eindeutigen Knoten verbunden ist. Azyklische Graphen werden auch als azyklische Graphen bezeichnet.

Der Unterschied zwischen zyklischen und azyklischen Diagrammen -

Die chinesische Übersetzung von lautet:

Cycle Graph	Cycle Graph	Azyklischer Graph
Der Graph bildet eine geschlossene Schleife.	Das Diagramm bildet keinen geschlossenen Kreislauf.
Deep Loops sind nicht im Diagramm enthalten	Charts enthalten jede Tiefe.

Beispiel 1

Nehmen wir ein Beispiel für einen zyklischen Graphen −

Wenn eine geschlossene Schleife existiert, wird ein zyklischer Graph gebildet.

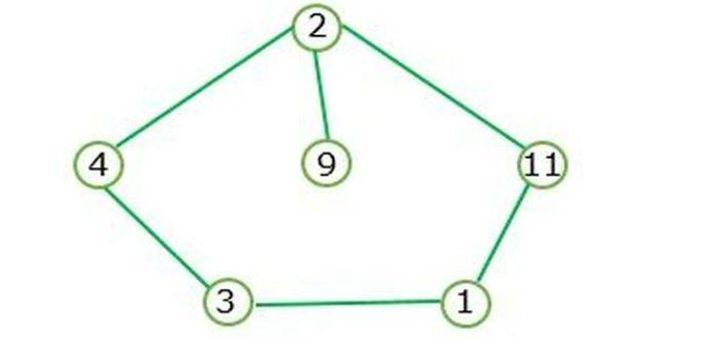
Abbildung I stellt das Zyklusdiagramm dar und enthält keine Tiefenknoten.

Beispiel 2

wird übersetzt als:

Beispiel 2

Lassen Sie uns dies anhand eines Beispiels eines azyklischen Diagramms veranschaulichen:

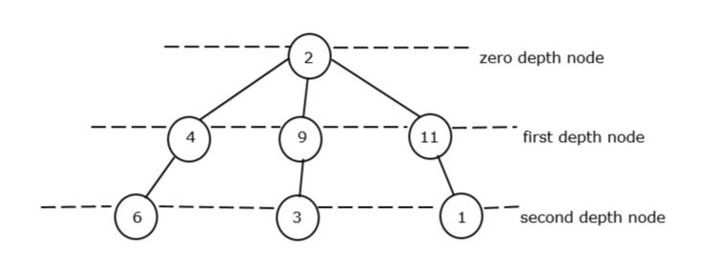
Der Wurzelknoten des Baums wird als Null-Tiefe-Knoten bezeichnet. In Abbildung II gibt es nur eine Wurzel in der Tiefe Null, nämlich 2. Daher wird er als Knoten mit einer Mindesttiefe von Null betrachtet.

Im ersten Tiefenknoten haben wir 3 Knotenelemente wie 4, 9 und 1, aber das kleinste Element ist 4.

Im zweiten Tiefenknoten haben wir wieder 3 Knotenelemente wie 6, 3 und 1, aber das minimale Element ist 1.

Wir werden wissen, wie der Gesamttiefenknoten abgeleitet wird,

Gesamttiefenknoten = Mindestwert des Zero_Depth-Knotens + Mindestwert des First_Depth-Knotens + Mindestwert des Zero_Depth-Knotens

Gesamttiefe Knoten = 2 + 4 + 3 = 9. Somit ist 9 die minimale Gesamtsumme des azyklischen Graphen.

Grammatik

The following syntax used in the program:
struct name_of_structure{
   data_type var_name;   
   // data member or field of the structure.
}

• struct – Dieses Schlüsselwort wird verwendet, um den Strukturdatentyp darzustellen.

• name_of_struct – Wir geben einen beliebigen Namen für die Struktur an.

• Eine Struktur ist eine Sammlung verschiedener verwandter Variablen an einem Ort.

Queue < pair < datatype, datatype> > queue_of_pair

make_pair() 

Parameter

Paarwarteschlange in C++ -

• Dies ist eine generische STL-Vorlage zum Kombinieren von Warteschlangenpaaren zweier verschiedener Datentypen. Die Warteschlangenpaare befinden sich unter der Utility-Header-Datei.

• Queue_of_pair - Wir geben dem Paar einen beliebigen Namen.

• make_pair() – wird verwendet, um ein Paarobjekt mit zwei Elementen zu erstellen.

name_of_queue.push()

Parameter

• name_of_queue – Wir benennen den Namen der Warteschlange.

• push() − Dies ist eine vordefinierte Methode, die Teil des Warteschlangenkopfes ist. Die Push-Methode wird zum Einfügen von Elementen oder Werten verwendet.

name_of_queue.pop()

Parameter

• name_of_queue − Wir geben der Warteschlange einen Namen.

• pop() - Dies ist eine vordefinierte Methode, die zur Warteschlangen-Header-Datei gehört, und die Pop-Methode wird verwendet, um das gesamte Element oder den gesamten Wert zu löschen.

Algorithmus

• Wir starten die Programm-Header-Dateien, nämlich 'iostream', 'climits', 'utility', und 'queue'.

  < /里>

• Wir erstellen die Struktur "tree_node" mit dem ganzzahligen Wert "val", um den Knotenwert zu erhalten. Anschließend erstellen wir einen tree_node pointer mit den angegebenen Daten, um die linken und rechten untergeordneten Knoten zum Speichern der Werte zu initialisieren. Als Nächstes erstellen wir eine Funktion „tree_node“, bei der int Jetzt definieren wir eine Funktion

  minimum_sum_at_each_third()
, die einen ganzzahligen Wert als Argument akzeptiert, um die Mindestsumme in jeder Tiefe zu ermitteln. Mithilfe einer if-Anweisung prüft es, ob der Stammwert des Baums leer ist, und gibt 0 zurück, wenn er leer ist.

• Wir erstellen Warteschlangenpaare von STL (Standard Template Library), um zwei Werte zu kombinieren.

• Wir erstellen eine Warteschlangenvariable namens q, die zwei Methoden als Paar akzeptiert, nämlich

  push()
und
• make_pair()

  . Mit diesen beiden Methoden fügen wir Werte ein und konstruieren zwei Paare eines Objekts. Wir initialisieren drei Variablen, nämlich „present_ Depth“, „present_sum“ und „totalSum“, die verwendet werden, um die aktuelle Summe weiter zu ermitteln und die Gesamtminimumsumme zu ermitteln.

• Nach der Initialisierung der Variablen erstellen wir eine While-Schleife, um die Bedingung zu überprüfen. Wenn das Warteschlangenpaar nicht leer ist, beginnt die Zählung der Knoten von vorne. Als nächstes verwenden wir die Methode

  ‘pop()‘
, um einen vorhandenen Knoten zu entfernen, da dieser in die nächste Tiefe des Baums verschoben wird, um die Mindestsumme zu berechnen.

• Jetzt erstellen wir drei if-Anweisungen, um die Mindestsumme der Summen zurückzugeben.

• Danach starten wir die Hauptfunktion und bauen die Baumstruktur des Eingabemodus mit Hilfe des Wurzelzeigers, des linken bzw. rechten Unterknotens, auf und übergeben den Knotenwert durch den neuen

  ‘tree_node‘
.

• Schließlich rufen wir die Funktion

  ‘minimum_sum_at_each_third(root)‘
auf und übergeben den Parameter root, um die Mindestsumme in jeder Tiefe zu berechnen. Drucken Sie als Nächstes die Anweisung „Summe jeder Tiefe des azyklischen Graphen“ aus und erhalten Sie das Ergebnis.

• Denken Sie daran, dass eine Paarwarteschlange ein Container ist, der Paare von Warteschlangenelementen enthält.

  Die chinesische Übersetzung von
Beispiel

lautet:

Beispiel

In diesem Programm berechnen wir die Summe aller Mindestknoten für jede Tiefe.

In Abbildung 2 beträgt die Mindestsumme der Gesamttiefe 15+8+4+1 = 13.

现在我们将把这个数字作为该程序的输入。

#include <iostream>
#include <queue> 

// required for FIFO operation
#include <utility> 

// required for queue pair
#include <climits>
using namespace std;

// create the structure definition for a binary tree node of non-cycle graph
struct tree_node {
   int val;
   tree_node *left;
   tree_node *right;
   tree_node(int x) {
      val = x;
      left = NULL;
      right = NULL;
   }
};
// This function is used to find the minimum sum at each depth
int minimum_sum_at_each_depth(tree_node* root) {
   if (root == NULL) {
      return 0;
   }
   queue<pair<tree_node*, int>> q;
   // create a queue to store node and depth and include pair to combine two together values.
   q.push(make_pair(root, 0)); 
   
   // construct a pair object with two element
   int present_depth = -1; 
   
   // present depth
   int present_sum = 0; 
   
   // present sum for present depth
   int totalSum = 0; 
   
   // Total sum for all depths
   while (!q.empty()) {
      pair<tree_node*, int> present = q.front(); 
      
      // assign queue pair - present
      q.pop();
      
      // delete an existing element from the beginning
      if (present.second != present_depth) {
      
         // We are moving to a new depth, so update the total sum and reset the present sum
         present_depth = present.second;
         totalSum += present_sum;
         present_sum = INT_MAX;
      }

      // Update the present sum with the value of the present node
      present_sum = min(present_sum, present.first->val);
      
      //We are adding left and right children to the queue for updating the new depth.
      if (present.first->left) {
         q.push(make_pair(present.first->left, present.second + 1));
      }
      if (present.first->right) {
         q.push(make_pair(present.first->right, present.second + 1));
      }
   }
   
   // We are adding the present sum of last depth to the total sum
   totalSum += present_sum;
   return totalSum;
}

// start the main function
int main() {
   tree_node *root = new tree_node(15);
   root->left = new tree_node(14);
   root->left->left = new tree_node(11);
   root->left->right = new tree_node(4);
   root->right = new tree_node(8);
   root->right->left = new tree_node(13);
   root->right->right = new tree_node(16);
   root->left->left->left = new tree_node(1);
   root->left->right->left = new tree_node(6);
   root->right->right->right = new tree_node(2);
   root->right->left->right = new tree_node(7);

   cout << "Total sum at each depth of non cycle graph: " << minimum_sum_at_each_depth(root) << endl; 
   return 0;
}

输出

Total sum at each depth of non cycle graph: 28

结论

我们探讨了给定非循环图中每个深度的元素最小和的概念。我们看到箭头运算符连接节点并构建树形结构，利用它计算每个深度的最小和。该应用程序使用非循环图，例如城市规划、网络拓扑、谷歌地图等。

Das obige ist der detaillierte Inhalt vonBerechnen Sie bei einem gegebenen azyklischen Graphen die minimale Summe der Elemente in jeder Tiefe. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!