Das Training und die Feinabstimmung großer Modelle stellt hohe Anforderungen an den Videospeicher, und der Optimierungsstatus ist einer der Hauptkosten des Videospeichers. Kürzlich hat das Team von Zhu Jun und Chen Jianfei von der Tsinghua-Universität einen 4-Bit-Optimierer für das Training neuronaler Netze vorgeschlagen, der den Speicheraufwand beim Modelltraining einspart und eine Genauigkeit erreichen kann, die mit der eines Vollpräzisionsoptimierers vergleichbar ist.
Der 4-Bit-Optimierer wurde an zahlreichen Vortrainings- und Feinabstimmungsaufgaben experimentiert und reduziert den Speicheraufwand für die Feinabstimmung von LLaMA-7B um bis zu 57 %, während die Genauigkeit erhalten bleibt.
Papier: https://arxiv.org/abs/2309.01507
Code: https://github.com/thu-ml/low-bit-optimizers
Von GPT-3, Gopher bis LLaMA ist es ein Branchenkonsens geworden, dass große Modelle eine bessere Leistung haben. Im Gegensatz dazu ist die Videospeichergröße einer einzelnen GPU jedoch langsam gewachsen, was den Videospeicher zum Hauptengpass für das Training großer Modelle macht. Das Trainieren großer Modelle mit begrenztem GPU-Speicher ist zu einem wichtigen Problem geworden.
Dazu müssen wir zunächst die Quellen des Videospeicherverbrauchs klären. Tatsächlich gibt es drei Arten von Quellen, nämlich:
1. „Datenspeicher“, einschließlich der Eingabedaten und des von jeder Schicht des neuronalen Netzwerks ausgegebenen Aktivierungswerts, dessen Größe direkt von der Stapelgröße beeinflusst wird Bildauflösung/Kontextlänge
2. „Modellspeicher“, einschließlich Modellparameter, Verläufe und Optimiererzustände, seine Größe ist proportional zur Anzahl der Modellparameter
3 GPU Temporärer Speicher und andere Caches, die in Kernel-Berechnungen verwendet werden. Mit zunehmender Größe des Modells nimmt der Anteil des Videospeichers des Modells allmählich zu, was zu einem großen Engpass wird.
Die Größe des Optimiererstatus wird dadurch bestimmt, welcher Optimierer verwendet wird. Derzeit werden AdamW-Optimierer häufig zum Trainieren von Transformern verwendet, die während des Trainingsprozesses zwei Optimiererzustände speichern und aktualisieren müssen, nämlich den ersten und den zweiten Moment. Wenn die Anzahl der Modellparameter N beträgt, beträgt die Anzahl der Optimiererzustände in AdamW 2N, was offensichtlich einen enormen Grafikspeicheraufwand darstellt.
Nehmen Sie LLaMA-7B als Beispiel. Die Anzahl der Parameter dieses Modells beträgt etwa 7B. Wenn der AdamW-Optimierer mit voller Präzision zur Feinabstimmung verwendet wird, beträgt die vom Optimierer belegte Speichergröße Der Status beträgt etwa 52,2 GB. Obwohl der naive SGD-Optimierer keine zusätzlichen Zustände benötigt und den vom Optimiererzustand belegten Speicher spart, ist es außerdem schwierig, die Leistung des Modells zu garantieren. Daher konzentriert sich dieser Artikel darauf, wie der Optimiererstatus im Modellspeicher reduziert und gleichzeitig sichergestellt wird, dass die Leistung des Optimierers nicht beeinträchtigt wird.
Derzeit gibt es in Bezug auf Trainingsalgorithmen drei Hauptmethoden, um Optimiererspeicheraufwand zu sparen:
1 Analysieren Sie den Optimiererstatus durch die Idee von Low- Rangzerlegung (Faktorisierung) Führen Sie eine Approximation mit niedrigem Rang durch. Präzises numerisches Format zur Darstellung des Optimiererstatus.
Insbesondere haben Dettmers et al. (ICLR 2022) einen entsprechenden 8-Bit-Optimierer für SGD mit Impuls und AdamW vorgeschlagen, der durch die Verwendung blockweiser Quantisierung und der Technologie des dynamischen exponentiellen numerischen Formats erreicht wurde Ergebnisse, die mit dem ursprünglichen Optimierer mit voller Präzision bei Aufgaben wie Sprachmodellierung, Bildklassifizierung, selbstüberwachtem Lernen und maschineller Übersetzung übereinstimmen.
Auf dieser Grundlage reduziert dieser Artikel die numerische Genauigkeit des Optimiererzustands weiter auf 4 Bit, schlägt Quantisierungsmethoden für verschiedene Optimiererzustände vor und schlägt schließlich einen 4-Bit-AdamW-Optimierer vor. Gleichzeitig untersucht dieser Artikel die Möglichkeit der Kombination von Komprimierungs- und Low-Rank-Zerlegungsmethoden und schlägt einen 4-Bit-Faktoroptimierer vor. Dieser Hybridoptimierer bietet sowohl eine gute Leistung als auch eine bessere Speichereffizienz. In diesem Artikel werden 4-Bit-Optimierer für eine Reihe klassischer Aufgaben bewertet, darunter das Verständnis natürlicher Sprache, die Bildklassifizierung, die maschinelle Übersetzung und die Feinabstimmung von Anweisungen großer Modelle.
Bei allen Aufgaben erzielt der 4-Bit-Optimierer vergleichbare Ergebnisse wie der Vollpräzisionsoptimierer und belegt dabei weniger Speicher.
Problem-Setup
Ein Framework für einen komprimierungsbasierten speichereffizienten Optimierer
Zunächst müssen wir verstehen, wie Komprimierungsvorgänge in häufig verwendete Optimierer eingeführt werden, was durch Algorithmus 1 gegeben ist. Dabei ist A ein auf Gradienten basierender Optimierer (z. B. SGD oder AdamW). Der Optimierer übernimmt die vorhandenen Parameter w, den Gradienten g und den Optimiererstatus s und gibt neue Parameter und den Optimiererstatus aus. In Algorithmus 1 ist s_t mit voller Genauigkeit vorübergehend, während (s_t) ̅ mit niedriger Genauigkeit im GPU-Speicher gespeichert bleibt. Der wichtige Grund, warum diese Methode Videospeicher sparen kann, besteht darin, dass die Parameter neuronaler Netze häufig aus den Parametervektoren jeder Schicht zusammengefügt werden. Daher wird die Aktualisierung des Optimierers auch Schicht für Schicht/Tensor durchgeführt. Bei Algorithmus 1 bleibt der Optimiererstatus von höchstens einem Parameter in Form von voller Präzision im Speicher, und die Optimiererzustände, die anderen Schichten entsprechen, sind komprimiert Zustand. .
Hauptkomprimierungsmethode: Quantisierung
Quantisierung ist eine Technologie, die numerische Werte mit geringer Genauigkeit verwendet, um hochpräzise Daten darzustellen. Dieser Artikel entkoppelt den Quantisierungsvorgang in zwei Teile: Normalisierung ( Normalisierung) und Mapping (Mapping) und ermöglichen so ein leichteres Design und Experimentieren mit neuen Quantifizierungsmethoden. Zwei Operationen, Normalisierung und Zuordnung, werden nacheinander elementweise auf die Daten mit voller Genauigkeit angewendet. Die Normalisierung ist dafür verantwortlich, jedes Element im Tensor auf das Einheitsintervall zu projizieren, wobei Tensornormalisierung (Pro-Tensor-Normalisierung) und blockweise Normalisierung (blockweise Normalisierung) wie folgt definiert sind:
Verschiedene Normalisierungsmethoden haben unterschiedliche Granularitäten, ihre Fähigkeit, Ausreißer zu verarbeiten, ist unterschiedlich und sie verursachen auch unterschiedlichen zusätzlichen Speicheraufwand. Die Zuordnungsoperation ist für die Zuordnung normalisierter Werte zu Ganzzahlen verantwortlich, die mit geringer Genauigkeit dargestellt werden können. Formal gesehen ist die Zuordnungsoperation bei gegebener Bitbreite b (d. h. jeder Wert wird durch b Bits nach der Quantisierung dargestellt) und einer vordefinierten Funktion T
wie folgt definiert:
Daher gilt: Wie richtig entworfen T spielt eine wichtige Rolle bei der Reduzierung von Quantisierungsfehlern. In diesem Artikel werden hauptsächlich die lineare Abbildung (linear) und die dynamische exponentielle Abbildung (dynamischer Exponent) betrachtet. Schließlich besteht der Prozess der Dequantisierung darin, die inversen Operatoren der Abbildung und Normalisierung nacheinander anzuwenden.
Im Folgenden werden hauptsächlich verschiedene Quantisierungsmethoden für den Optimiererzustand (Moment erster Ordnung und Moment zweiter Ordnung) von AdamW vorgeschlagen. Zunächst einmal basiert die Quantisierungsmethode in diesem Artikel hauptsächlich auf der Methode von Dettmers et al. (ICLR 2022) und verwendet Blocknormalisierung (Blockgröße 2048) und dynamische exponentielle Abbildung.
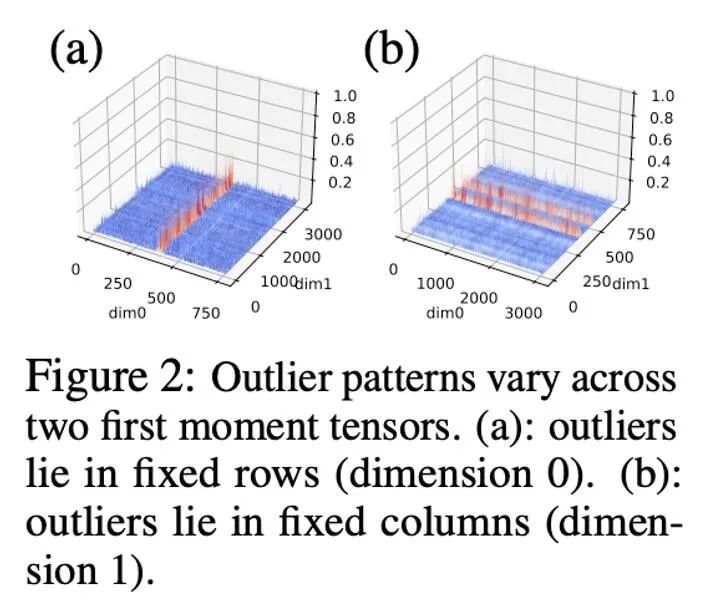
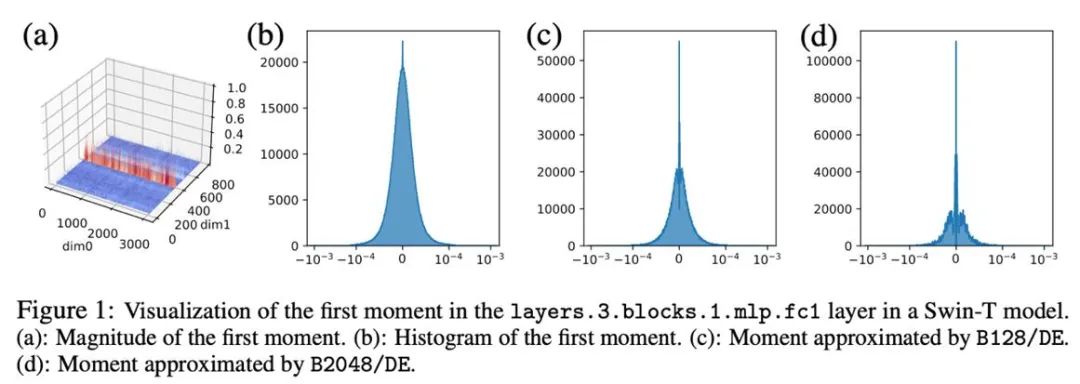
In Vorversuchen haben wir die Bitbreite direkt von 8 Bit auf 4 Bit reduziert und festgestellt, dass das Moment erster Ordnung sehr robust gegenüber der Quantisierung ist und bei vielen Aufgaben Anpassungseffekte erzielt hat, aber auch bei einigen Aufgaben auftritt. Leistungsverlust. Um die Leistung weiter zu verbessern, haben wir das Muster der ersten Momente sorgfältig untersucht und festgestellt, dass es in einem einzelnen Tensor viele Ausreißer gibt.
In früheren Arbeiten wurden einige Untersuchungen zum Muster von Ausreißern in Parametern und Aktivierungswerten durchgeführt. Die Verteilung der Parameter ist relativ gleichmäßig, während die Aktivierungswerte nach Kanälen verteilt sind. In diesem Artikel wurde festgestellt, dass die Verteilung von Ausreißern im Optimiererzustand komplex ist, wobei bei einigen Tensoren die Ausreißer in festen Zeilen und bei anderen Tensoren in festen Spalten verteilt sind.
Bei Tensoren mit spaltenweiser Verteilung von Ausreißern kann die Blocknormalisierung in der ersten Zeile auf Schwierigkeiten stoßen. Daher wird in diesem Artikel vorgeschlagen, kleinere Blöcke mit einer Blockgröße von 128 zu verwenden, was den Quantisierungsfehler reduzieren und gleichzeitig den zusätzlichen Speicheraufwand in einem kontrollierbaren Bereich halten kann. Die folgende Abbildung zeigt den Quantisierungsfehler für verschiedene Blockgrößen.
Im Vergleich zu Momenten erster Ordnung ist die Quantisierung von Momenten zweiter Ordnung schwieriger und führt zu Instabilität beim Training. In diesem Artikel wird festgestellt, dass das Nullpunktproblem der Hauptengpass bei der Quantifizierung von Momenten zweiter Ordnung ist. Darüber hinaus wird eine verbesserte Normalisierungsmethode für schlecht konditionierte Ausreißerverteilungen vorgeschlagen: Rang-1-Normalisierung. In diesem Artikel wird auch die Zerlegungsmethode (Faktorisierung) des Moments zweiter Ordnung versucht.
Nullpunktproblem
Bei der Quantisierung von Parametern, Aktivierungswerten und Gradienten sind Nullpunkte oft unverzichtbar und nach der Quantisierung auch die Punkte mit der höchsten Häufigkeit. In Adams iterativer Formel ist die Größe der Aktualisierung jedoch proportional zur -1/2-Potenz des zweiten Moments, sodass Änderungen im Bereich um Null die Größe der Aktualisierung stark beeinflussen und zu Instabilität führen.
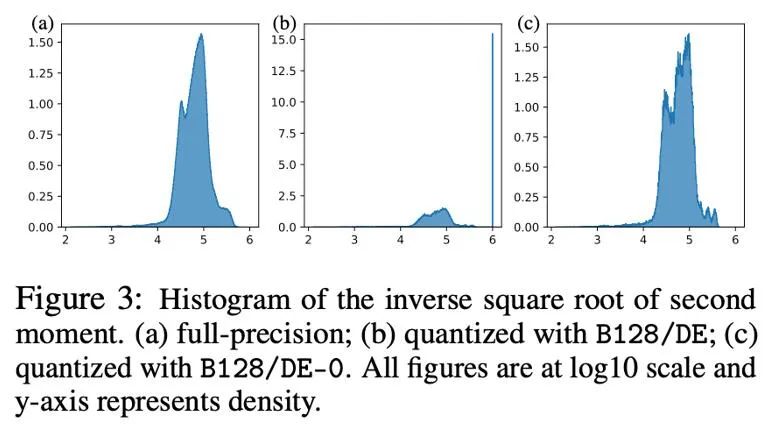
Die folgende Abbildung zeigt die Verteilung von Adams zweitem Moment -1/2 Potenz vor und nach der Quantisierung in Form eines Histogramms, d. h. h (v)=1/(√v+10^( -6) ) . Wenn die Nullen enthalten sind (Abbildung b), werden die meisten Werte auf 10^6 hochgeschoben, was zu großen Approximationsfehlern führt. Ein einfacher Ansatz besteht darin, die Nullstellen in der dynamischen Exponentialkarte zu entfernen. Danach (Abbildung c) wird die Annäherung an das zweite Moment genauer. Um in tatsächlichen Situationen die Ausdrucksfähigkeit numerischer Werte mit geringer Genauigkeit effektiv zu nutzen, haben wir vorgeschlagen, eine lineare Abbildung zu verwenden, die Nullpunkte entfernt, und haben in Experimenten gute Ergebnisse erzielt.
Rang-1-Normalisierung
Basierend auf der komplexen Ausreißerverteilung von Momenten erster und zweiter Ordnung und inspiriert vom SM3-Optimierer schlägt dieses Papier eine neue Normalisierungsmethode vor wird als Rang-1-Normalisierung bezeichnet. Für einen nicht negativen Matrixtensor x∈R^(n×m) ist seine eindimensionale Statistik wie folgt definiert:
Dann kann die Rang-1-Normalisierung wie folgt definiert werden:
Rang-1-Normalisierung nutzt die eindimensionalen Informationen des Tensors feinkörniger aus und kann zeilen- oder spaltenweise Ausreißer intelligenter und effizienter verarbeiten. Darüber hinaus kann die Rang-1-Normalisierung leicht auf hochdimensionale Tensoren verallgemeinert werden, und mit zunehmender Tensorgröße ist der dadurch erzeugte zusätzliche Speicheraufwand geringer als der der Blocknormalisierung.
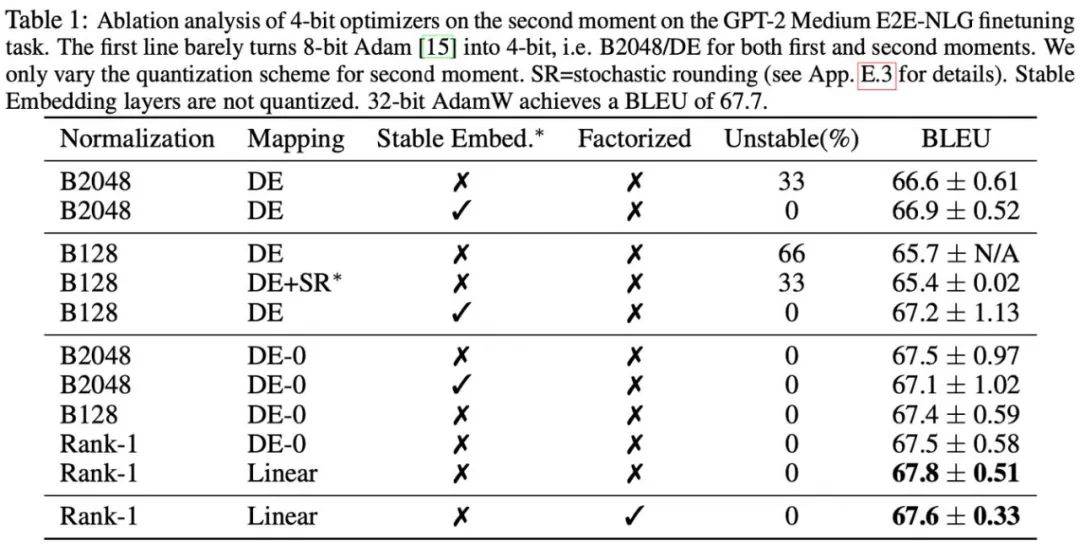
Darüber hinaus wurde in diesem Artikel festgestellt, dass die Low-Rank-Zerlegungsmethode für Momente zweiter Ordnung im Adafactor-Optimierer das Nullpunktproblem effektiv vermeiden kann, sodass auch die Kombination von Low-Rank-Zerlegungs- und Quantisierungsmethoden untersucht wurde. Die folgende Abbildung zeigt eine Reihe von Ablationsexperimenten für Momente zweiter Ordnung, die bestätigen, dass das Nullpunktproblem den Engpass bei der Quantifizierung von Momenten zweiter Ordnung darstellt. Außerdem wird die Wirksamkeit von Rang-1-Normalisierungs- und Niederrang-Zerlegungsmethoden bestätigt.
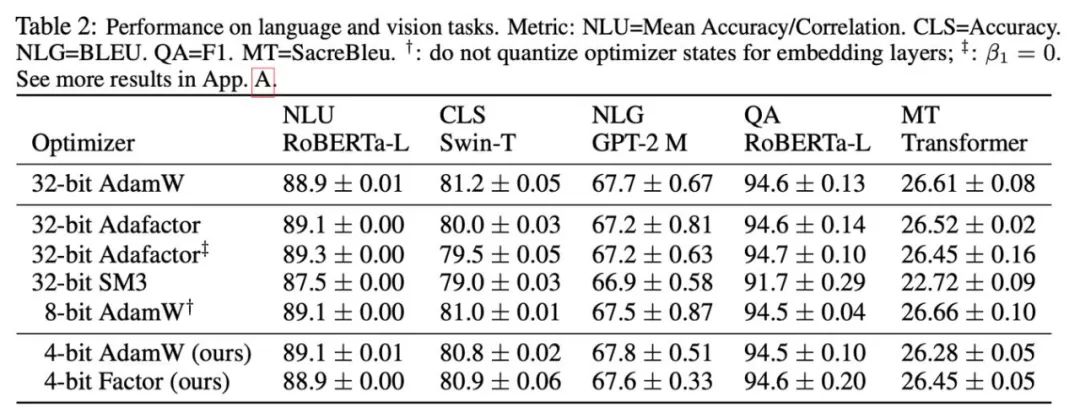
Basierend auf den beobachteten Phänomenen und Verwendungsmethoden schlug die Forschung schließlich zwei Optimierer mit geringer Präzision vor: 4-Bit-AdamW und 4-Bit-Faktor, und verglich sie mit anderen Optimierern. einschließlich 8-Bit AdamW, Adafactor, SM3. Es wurden Studien für die Evaluierung einer breiten Palette von Aufgaben ausgewählt, darunter das Verständnis natürlicher Sprache, Bildklassifizierung, maschinelle Übersetzung und die Feinabstimmung von Anweisungen für große Modelle. Die folgende Tabelle zeigt die Leistung jedes Optimierers bei verschiedenen Aufgaben.
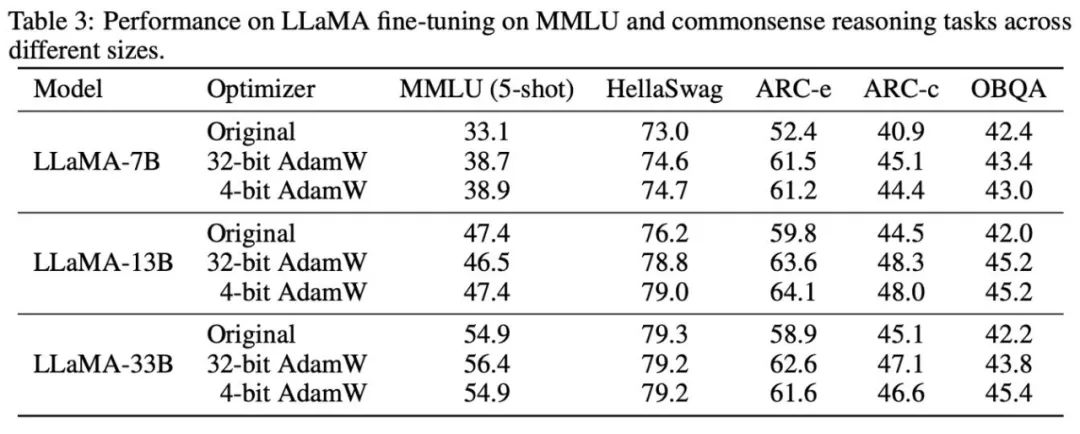
Es ist ersichtlich, dass der 4-Bit-Optimierer bei allen Feinabstimmungsaufgaben, einschließlich NLU, QA, NLG, mit dem 32-Bit-AdamW mithalten oder ihn sogar übertreffen kann, während er bei allen Vor- Bei Trainingsaufgaben erreicht der CLS-, MT- und 4-Bit-Optimierer ein Niveau, das mit der vollen Genauigkeit vergleichbar ist. Aus der Aufgabe zur Feinabstimmung von Anweisungen ist ersichtlich, dass 4-Bit-AdamW die Fähigkeit der vorab trainierten Modelle nicht zerstört und ihnen gleichzeitig die Fähigkeit zur Befolgung von Anweisungen besser ermöglichen kann.
Danach haben wir den Speicher und die Recheneffizienz des 4-Bit-Optimierers getestet. Die Ergebnisse sind in der folgenden Tabelle aufgeführt. Im Vergleich zum 8-Bit-Optimierer kann der in diesem Artikel vorgeschlagene 4-Bit-Optimierer mehr Speicher einsparen, mit einer maximalen Einsparung von 57,7 % im LLaMA-7B-Feinabstimmungsexperiment. Darüber hinaus bieten wir eine Fusionsoperatorversion von 4-Bit-AdamW an, die Speicher sparen kann, ohne die Recheneffizienz zu beeinträchtigen. Für die Befehlsfeinabstimmungsaufgabe von LLaMA-7B bringt 4-Bit-AdamW aufgrund des reduzierten Cache-Drucks auch Beschleunigungseffekte in das Training. Detaillierte experimentelle Einstellungen und Ergebnisse finden Sie im Paper-Link. Ersetzen Sie eine Codezeile, um sie in PyTorch zu verwenden unterstützt Versionen von Adam und SGD mit niedriger Genauigkeit. Gleichzeitig stellen wir auch eine Schnittstelle zum Modifizieren von Quantisierungsparametern zur Verfügung, um individuelle Nutzungsszenarien zu unterstützen.
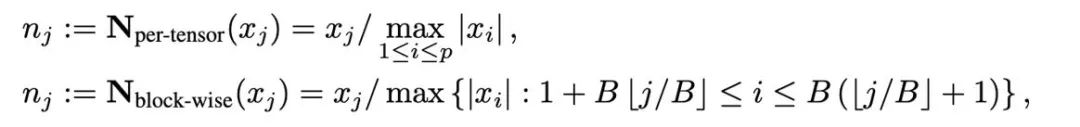
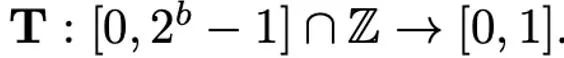
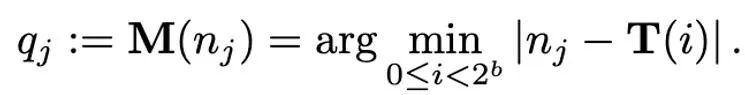
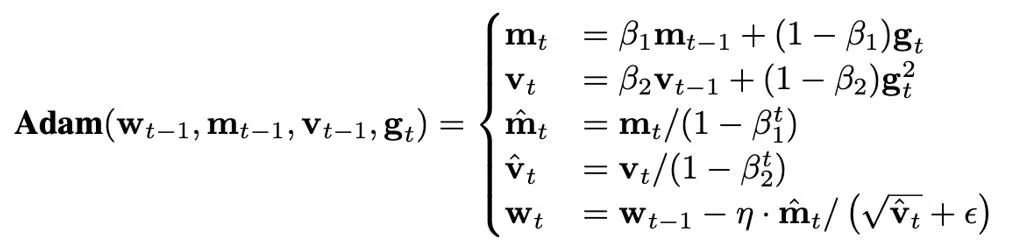
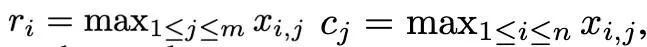
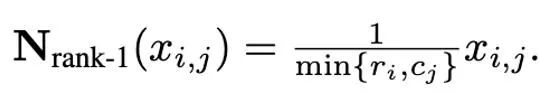
Das obige ist der detaillierte Inhalt vonDie Feinabstimmung von LLaMA reduziert den Speicherbedarf um die Hälfte, Tsinghua schlägt einen 4-Bit-Optimierer vor. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
Java-Multithread-Programmierung
Vier Hauptmerkmale der Blockchain
Drei Formen bedingter Anweisungen
Was ist Maschinensprache?
Lösung für den Failedtofetch-Fehler
Der Unterschied zwischen Get-Request und Post-Request
Der Unterschied zwischen Pascal-Sprache und C-Sprache
Linux fügt die Update-Quellenmethode hinzu
