Übersetzen Sie im C-Programm den folgenden Inhalt ins Chinesische: Programm zum Suchen des n-ten Knotens am Ende einer verknüpften Liste

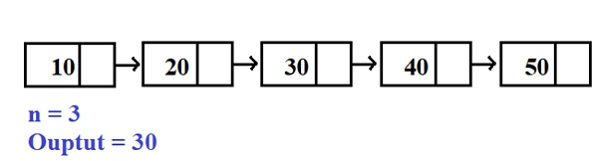
Bei n Knoten besteht die Aufgabe darin, den n-ten Knoten am Ende der verknüpften Liste zu drucken. Das Programm darf die Reihenfolge der Knoten in der Liste nicht ändern, sondern sollte nur den n-ten Knoten vom letzten Knoten der verknüpften Liste ausdrucken.

Beispiel

Input -: 10 20 30 40 50 60
   N=3
Output -: 40

Im obigen Beispiel wird ausgehend vom ersten Knoten zu Knoten mit der Anzahl n durchlaufen, d. h. 10,20 30,40, 50,60, sodass der drittletzte Knoten 40 ist.

Anstatt die gesamte Liste so effizient zu durchlaufen, können Sie dem Ansatz folgen:

• Erhalten Sie einen temporären Zeiger auf beispielsweise die Temperatur des Knotentyps.
• Setzen Sie diesen temporären Zeiger auf den ersten Knotenkopfzeiger, auf den gezeigt wird ?? die Schleife bis 5-3, was 2 ist, also beginnend mit 10 an der 0
.
• Position, bis 20 zur 1. Position und die 30. Position zur zweiten Position führt. Bei diesem Ansatz ist es also nicht erforderlich, die gesamte Liste bis zum Ende zu durchlaufen, was Platz und Speicher spart.
• Algorithmus

Start
Step 1 -> create structure of a node and temp, next and head as pointer to a structure node
   struct node
      int data
      struct node *next, *head, *temp
   End
Step 2 -> declare function to insert a node in a list
   void insert(int val)
      struct node* newnode = (struct node*)malloc(sizeof(struct node))
      newnode->data = val
      IF head= NULL
         set head = newnode
         set head->next = NULL
      End
      Else
         Set temp=head
         Loop While temp->next!=NULL
            Set temp=temp->next
         End
         Set newnode->next=NULL
         Set temp->next=newnode
      End
Step 3 -> Declare a function to display list
   void display()
      IF head=NULL
         Print no node
      End
      Else
         Set temp=head
         Loop While temp!=NULL
            Print temp->data
            Set temp=temp->next
         End
      End
Step 4 -> declare a function to find nth node from last of a linked list
   void last(int n)
      declare int product=1, i
      Set temp=head
      Loop For i=0 and i<count-n and i++
         Set temp=temp->next
      End
      Print temp->data
Step 5 -> in main()
   Create nodes using struct node* head = NULL
   Declare variable n as nth to 3
   Call function insert(10) to insert a node
   Call display() to display the list
   Call last(n) to find nth node from last of a list
Stop

• Beispiel

Live-Demonstration

#include<stdio.h>
#include<stdlib.h>
//structure of a node
struct node{
   int data;
   struct node *next;
}*head,*temp;
int count=0;
//function for inserting nodes into a list
void insert(int val){
   struct node* newnode = (struct node*)malloc(sizeof(struct node));
   newnode->data = val;
   newnode->next = NULL;
   if(head == NULL){
      head = newnode;
      temp = head;
      count++;
   } else {
      temp->next=newnode;
      temp=temp->next;
      count++;
   }
}
//function for displaying a list
void display(){
   if(head==NULL)
      printf("no node ");
   else {
      temp=head;
      while(temp!=NULL) {
         printf("%d ",temp->data);
         temp=temp->next;
      }
   }
}
//function for finding 3rd node from the last of a linked list
void last(int n){
   int i;
   temp=head;
   for(i=0;i<count-n;i++){
      temp=temp->next;
   }
   printf("</p><p>%drd node from the end of linked list is : %d" ,n,temp->data);
}
int main(){
   //creating list
   struct node* head = NULL;
   int n=3;
   //inserting elements into a list
   insert(1);
   insert(2);
   insert(3);
   insert(4);
   insert(5);
   insert(6);
   //displaying the list
   printf("</p><p>linked list is : ");
   display();
   //calling function for finding nth element in a list from last
   last(n);
   return 0;
}

^Ausgabe

linked list is : 1 2 3 4 5 6
3rd node from the end of linked list is : 4

Das obige ist der detaillierte Inhalt vonÜbersetzen Sie im C-Programm den folgenden Inhalt ins Chinesische: Programm zum Suchen des n-ten Knotens am Ende einer verknüpften Liste. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!