Ein Zahlenspiel?
Number Connect ist ein Logikrätsel, bei dem es darum geht, Wege zu finden, die Zahlen in einem Raster verbinden.
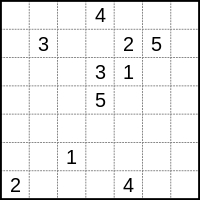
Ein einfaches Beispiel für ein Numberlink-Rätsel. Lösung für ein Numberlink-Rätsel.
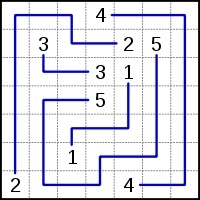
Regeln: Die Spieler müssen alle übereinstimmenden Zahlen im Raster mit einer einzigen durchgehenden Linie (oder einem Pfad) zuordnen. Linien dürfen nicht auseinanderlaufen oder sich kreuzen, und die Zahlen müssen am Ende jeder Linie stehen (d. h. nicht in der Mitte). Ein Problem gilt nur dann als gut gestaltet, wenn es eine eindeutige Lösung hat und alle Zellen im Raster gefüllt sind, obwohl einige Numberlink-Designer dies nicht vorschreiben.
Spiel – Betrachten Sie eine n×n-Reihe von Quadraten. Einige der Quadrate sind leer, andere sind ausgefüllt und einige nicht ausgefüllte Quadrate sind durch die ganzen Zahlen 1, 2, 3, ... gekennzeichnet. Jede ganze Zahl belegt zwei verschiedene Felder auf der Tafel. Die Aufgabe des Spielers besteht darin, die beiden Vorkommen jeder Ganzzahl auf dem Spielbrett über einen einfachen Pfad zu verbinden, indem er nur horizontale und vertikale Bewegungen verwendet. Es ist nicht erlaubt, dass sich zwei unterschiedliche Wege kreuzen. Kein Pfad darf feste Blöcke enthalten (auf keinem Pfad sind feste Blöcke zulässig). Schließlich müssen alle nicht durchgezogenen Quadrate durch Pfade gefüllt werden.
Algorithmus – Um ein effizientes Zufallsrätsel bei einer Brettgröße n×n vorzubereiten, generieren wir zunächst zufällige einfache disjunkte Pfade auf dem Brett. Wenn es mehrere isolierte Blöcke gibt, die außerhalb aller generierten Pfade verbleiben, markieren Sie diese isolierten Blöcke als fest (verboten). Als Puzzle verwenden wir dann die Endpunkte des Pfades und die Liste der ausgefüllten Quadrate.
Also generieren wir zunächst eine Lösung und lösen dann aus der Lösung das Rätsel. Pfade und ausgefüllte Quadrate unterteilen das n×n-Schachbrett in Teile. Wir verwenden die Union-Lookup-Datenstruktur, um diese Aufteilung zu generieren. Die Datenstruktur verarbeitet eine Teilmenge von n^2 Feldern auf dem Schachbrett. Erklärung- Finden Sie zufällig Quadrate (i, j) und (k, l) auf dem Schachbrett, so dass: (a) (i, j) und (k, l) einander benachbart sind und (b ) Weder (i, j) noch (k, l) gehören zu einem der bisher generierten Pfade. Wenn auf der gesamten Tafel kein solches Quadratpaar gefunden wird, wird ein Fehler zurückgegeben /* Dabei sind (i, j) und (k, l) die ersten beiden Quadrate des neu zu konstruierenden Pfades. *
- Füge zwei Union-Find-Bäume zusammen, die (i, j) und (k, l) enthalten.
- Wiederholen Sie die folgenden Schritte, bis der aktuelle Pfad nicht mehr erweitert werden kann: Benennen Sie (i, j) in (k, l) um. Finden Sie zufällig die Nachbarquadrate (k, l) von (i, j), sodass: (a) (k, l) zu keinem bisher generierten Pfad gehört (einschließlich des aktuellen Pfads) (b) Auf dem aktuell konstruierten Pfad teilweise ( Der einzige Nachbar von i, j) ist (k, l).
- Wenn kein solches Nachbarquadrat (k, l) gefunden wird, kann der Pfad nicht weiter verlängert werden, sodass die Schleife unterbrochen wird
- Andernfalls ist die Vereinigung der beiden, die (i, j) und (k) enthält , l) wird der Suchsatzbaum zusammengeführt.
- Setzen Sie die Flags der Start- und Endblöcke des neuen Pfads.
- Rückgabe erfolgreich
Eingabe
| || || || || || || 4 | | || || || || || 3 || | | || || 2 || 2 || || || 3 | | || || || || X || || 1 | | || || 6 || || || 7 || 7 | | 5 || 4 || || X || || X || 1 | | || 5 || || 6 || || || |
Ausgabe
Lösung zur obigen Tabelle| 4 || 4 || 4 || 4 || 4 || 4 || 4 | | 4 || 1 || 1 || 1 || 1 || 3 || 3 | | 4 || 1 || 2 || 2 || 1 || 1 || 3 | | 4 || 1 || 1 || 1 || X || 1 || 1 | | 4 || 4 || 6 || 1 || 1 || 7 || 7 | | 5 || 4 || 6 || X || 1 || X || 1 | | 5 || 5 || 6 || 6 || 1 || 1 || 1 |
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
struct _node {
struct _node *parent;
int rank;
int path_number;
int endpoint;
};
typedef struct _node node;
/* Name: initboard()
Input: 2D-array of pointers, size of array row/column
Output: --void--
Description: Takes a table of pointers and initializes it. */
void initboard(node ***arr, int n) {
int i, j;
for (i=0;i<n;i++){
for (j=0;j<n;j++){
node *np;
np = (node *)malloc(sizeof(node));
np->rank = 0;
np->parent = NULL;
np->path_number = 0;
np->endpoint = 0;
arr[i][j] = np;
}
}
}
/*Nach dem Login kopieren
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
struct _node {
struct _node *parent;
int rank;
int path_number;
int endpoint;
};
typedef struct _node node;
/* Name: initboard()
Input: 2D-array of pointers, size of array row/column
Output: --void--
Description: Takes a table of pointers and initializes it. */
void initboard(node ***arr, int n) {
int i, j;
for (i=0;i<n;i++){
for (j=0;j<n;j++){
node *np;
np = (node *)malloc(sizeof(node));
np->rank = 0;
np->parent = NULL;
np->path_number = 0;
np->endpoint = 0;
arr[i][j] = np;
}
}
}
/*Input:a node Output:the set pointer of the set the node belongs to
Beschreibung – Ruft einen Knoten ab und gibt einen Set-Zeiger zurück . */
node *findset(node *n) {
if (n->parent != NULL)
n = n->parent;
return n;
}
void setunion(node *x, node *y) {
x = findset(x);
y = findset(y);
if (x->rank > y->rank)
y->parent = x;
else {
x->parent = y;
if(x->rank == y->rank)
y->rank++;
}
}
int neighbour(int n, node ***arr) {
int i1, i2, j1, j2, ct = 0, flag = 0, a, b,k2;
int k = rand()%(n*n);
while (ct < (n*n)) {
k %= (n*n);
i1 = k/n;
j1 = k%n;
if (arr[i1][j1]->path_number==0) {
int kk = rand()%4;
int cc = 0;
switch (kk) {
case 0: i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 1: i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 2: i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 3: i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 4: if(cc==4)
break;
i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 5: if(cc==4)
break;
i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 6: if(cc==4)
break;
i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 7: if(cc==4)
break;
i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
}
}
if(flag==1)
break;
ct++;
k++;
}
if(ct<n*n) {
k2= (i2*n)+j2;
return k*(n*n)+k2;
} else {
return -1;
}
}
int checkneigh(int k1, int k2, int n, node ***arr) {
int i= k2/n;
int j= k2%n;
int ii= k1/n;
int jj= k1%n;
int ct=0;
if(i>0 && findset(arr[i-1][j])==findset(arr[ii][jj]))
ct++;
if(i<n-1 && findset(arr[i+1][j])==findset(arr[ii][jj]))
ct++;
if(j>0 && findset(arr[i][j-1])==findset(arr[ii][jj]))
ct++;
if(j<n-1 && findset(arr[i][j+1])==findset(arr[ii][jj]))
ct++;
if(ct>1)
return 0;
else
return 1;
}
int valid_next(int k, int n, node ***arr) {
int i1, i2, j1, j2, a, b, kk, stat,ct=0;
int flag=0;
i1= k/n;
j1= k%n;
kk= rand()%4;
switch(kk) {
case 0: i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 1: i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 2: i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 3: i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 4: if(ct==4)
break;
i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 5: if(ct==4)
break;
i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 6: if(ct==4)
break;
i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 7: if(ct==4)
break;
i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
}
//printf("flag- %d</p><p>",flag);
if(flag==0)
return -1;
if(flag) {
//printf("value sent- %d</p><p>", i2*n + j2);
return (i2*n)+j2;
}
}
int addpath(node ***arr, int n, int ptno) {
int a,b,k1,k2;
int i1,j1,i2,j2;
k2= neighbour( n, arr);
if(k2==-1) //no valid pair found to start with
return 0;
k1= k2/(n*n);
k2= k2%(n*n);
//printf("%d %d</p><p>",k1,k2);
i1= k1/n;
j1= k1%n;
i2= k2/n;
j2= k2%n;
arr[i1][j1]->endpoint= 1;
arr[i2][j2]->path_number= ptno;
arr[i1][j1]->path_number= ptno;
node *n1, *n2;
n1= arr[i1][j1];
n2= arr[i2][j2];
n1= findset(n1);
n2= findset(n2);
setunion(n1, n2);
while(1) {
i1= i2;
j1= j2;
k1= (i1*n)+j1;
k2= valid_next(k1,n,arr);
if(k2==-1) {
arr[i1][j1]->endpoint= 1;
break;
}
i2=k2/n;
j2=k2%n;
arr[i2][j2]->path_number= ptno;
node *n1, *n2;
n1= arr[i1][j1];
n2= arr[i2][j2];
n1= findset(n1);
n2= findset(n2);
setunion(n1,n2);
}
return 1;
}
void printtable(node ***arr, int n) {
int i,j;
printf("Table to be solved:</p><p>");
for(i=0;i<n;i++) {
for(j=0;j<n;j++) {
if(arr[i][j]->endpoint ==1){
if(arr[i][j]->path_number/10==0)
printf("| %d |",arr[i][j]->path_number);
else
printf("| %d|",arr[i][j]->path_number);
} else if(arr[i][j]->path_number==0)
printf("| X |");
else
printf("| |");
}
printf("</p><p>");
}
printf("</p><p></p><p>The solution to the above table:</p><p>");
for(i=0;i<n;i++) {
for(j=0;j<n;j++) {
if(arr[i][j]->path_number != 0){
if(arr[i][j]->path_number/10==0)
printf("| %d |",arr[i][j]->path_number);
else
printf("| %d|",arr[i][j]->path_number);
} else
printf("| X |");
}
printf("</p><p>");
}
}
int main(void) {
srand((unsigned int) time (NULL));
int i, j;
int ct = 1;
int n = 7;
node*** pointers= (node ***)malloc(n*sizeof(node **));
for (i=0; i<n; i++)
pointers[i] = (node **)malloc(n*sizeof(node *));
initboard(pointers, n);
while(1) {
i = addpath(pointers, n, ct);
if (i==0) {
break;
} else {
ct++;
}
}
printtable(pointers,n);
return 0;
}Das obige ist der detaillierte Inhalt vonEin Zahlenspiel?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Nvgpucomp64.dll führt zum Absturz von Windows-PC-Spielen;
Mar 26, 2024 am 08:20 AM
Nvgpucomp64.dll führt zum Absturz von Windows-PC-Spielen;
Mar 26, 2024 am 08:20 AM
Wenn Nvgpucomp64.dll dazu führt, dass Ihr Spiel häufig abstürzt, können Ihnen die hier bereitgestellten Lösungen helfen. Dieses Problem wird normalerweise durch veraltete oder beschädigte Grafikkartentreiber, beschädigte Spieledateien usw. verursacht. Das Beheben dieser Probleme kann Ihnen dabei helfen, Spielabstürze zu beheben. Die Datei Nvgpucomp64.dll ist mit NVIDIA-Grafikkarten verknüpft. Wenn diese Datei abstürzt, stürzt auch Ihr Spiel ab. Dies geschieht normalerweise in Spielen wie LordsoftheFallen, LiesofP, RocketLeague und ApexLegends. Nvgpucomp64.dll stürzt Spiele auf Windows-PCs ab, wenn N
 Einführung in das Herunterladen und Installieren des Superpeople-Spiels
Mar 30, 2024 pm 04:01 PM
Einführung in das Herunterladen und Installieren des Superpeople-Spiels
Mar 30, 2024 pm 04:01 PM
Das Superpeople-Spiel kann über den Steam-Client heruntergeladen werden. Die Größe dieses Spiels beträgt normalerweise eineinhalb Stunden. Hier ist ein spezielles Download- und Installations-Tutorial. Neue Methode zur Beantragung globaler geschlossener Tests 1) Suchen Sie nach „SUPERPEOPLE“ im Steam-Store (Steam-Client-Download) 2) Klicken Sie unten auf der „SUPERPEOPLE“-Store-Seite auf „Zugriff auf geschlossene SUPERPEOPLE-Tests anfordern“ 3) Nachdem Sie auf geklickt haben Schaltfläche „Zugriff anfordern“. Das Spiel „SUPERPEOPLECBT“ kann in der Steam-Bibliothek bestätigt werden. 4) Klicken Sie auf die Schaltfläche „Installieren“ in „SUPERPEOPLECBT“ und laden Sie es herunter
 Wo ist Spider Solitaire in Win11? Wie spielt man das Spider Solitaire-Spiel in Win11?
Mar 01, 2024 am 11:37 AM
Wo ist Spider Solitaire in Win11? Wie spielt man das Spider Solitaire-Spiel in Win11?
Mar 01, 2024 am 11:37 AM
Freunde, die genug AAA-Meisterwerke und Handyspiele gespielt haben, möchten Sie die Computerspiele Ihrer Kindheit noch einmal erleben? Dann lasst uns gemeinsam nach Spider Solitaire in Windows 11 suchen! Klicken Sie auf der Benutzeroberfläche auf das Startmenü und dann auf die Schaltfläche „Alle Apps“. Suchen und wählen Sie „MicrosoftSolitaireCollection“, die Spieleanwendung der Solitaire-Serie von Microsoft. Nachdem der Ladevorgang abgeschlossen ist, rufen Sie die Auswahloberfläche auf und suchen Sie nach „Spider Solitaire“. Wählen Sie „Spider Solitaire“. Obwohl sich die Benutzeroberfläche geringfügig geändert hat, ist sie immer noch dieselbe wie zuvor
 ASUS veröffentlicht BIOS-Update zur Verbesserung der Spielestabilität auf Intels Prozessoren der 13./14. Generation
Apr 20, 2024 pm 05:01 PM
ASUS veröffentlicht BIOS-Update zur Verbesserung der Spielestabilität auf Intels Prozessoren der 13./14. Generation
Apr 20, 2024 pm 05:01 PM
Laut Nachrichten dieser Website vom 20. April hat ASUS kürzlich ein BIOS-Update veröffentlicht, das Instabilitäten wie Abstürze beim Ausführen von Spielen auf Intel-Prozessoren der 13./14. Generation verbessert. Diese Seite berichtete zuvor, dass Spieler Probleme gemeldet hätten, unter anderem, dass beim Ausführen der PC-Demoversion von Bandai Namcos Kampfspiel „Tekken 8“ das System abstürzte und eine Fehlermeldung über unzureichenden Speicher ausgab, selbst wenn der Computer über ausreichend Arbeits- und Videospeicher verfügte. Ähnliche Absturzprobleme traten auch in vielen Spielen wie „Battlefield 2042“, „Remnant 2“, „Fortnite“, „Lord of the Fallen“, „Hogwarts Legacy“ und „The Finals“ auf. RAD veröffentlichte im Februar dieses Jahres einen langen Artikel, in dem erklärt wurde, dass das Spielabsturzproblem eine Kombination aus BIOS-Einstellungen, hoher Taktfrequenz und hohem Stromverbrauch von Intel-Prozessoren ist.
 So deaktivieren Sie die Eingabemethode beim Spielen von Spielen unter Win11
Mar 15, 2024 pm 02:40 PM
So deaktivieren Sie die Eingabemethode beim Spielen von Spielen unter Win11
Mar 15, 2024 pm 02:40 PM
Kürzlich haben einige Freunde berichtet, dass sie beim Spielen häufig die Eingabemethode drücken, was das Spielerlebnis stark beeinträchtigt. Hier gebe ich Ihnen eine detaillierte Einführung in die Methode zum Deaktivieren der Eingabemethode beim Spielen in Win11 Freunde können vorbeikommen und einen Blick darauf werfen. Methode deaktivieren: 1. Klicken Sie mit der rechten Maustaste auf das Eingabemethodensymbol in der Taskleiste in der unteren rechten Ecke und wählen Sie „Spracheinstellungen“ in der Liste aus. 2. Nachdem Sie die neue Benutzeroberfläche aufgerufen haben, klicken Sie auf die Option „Bevorzugte Sprache hinzufügen“. 3. Wählen Sie im Popup-Fenster „Englisch (USA)“ aus. 4. Klicken Sie erneut auf „Weiter“. 5. Wählen Sie dann, ob Sie einige Optionen entsprechend Ihren Anforderungen installieren möchten. 6. Klicken Sie dann auf „Installieren“ und warten Sie, bis die Installation abgeschlossen ist. 7. Klicken Sie dann auf die Statusleiste der Eingabemethode in der unteren rechten Ecke und wählen Sie „Englisch (
 Der Update-Code „No Man's Sky' ebnete den Weg für die PS5 Pro und „überraschte' den Entwicklungscodenamen der Spielekonsole „Trinity' und die Konfigurationsdatei für die Bildqualität
Jul 22, 2024 pm 01:10 PM
Der Update-Code „No Man's Sky' ebnete den Weg für die PS5 Pro und „überraschte' den Entwicklungscodenamen der Spielekonsole „Trinity' und die Konfigurationsdatei für die Bildqualität
Jul 22, 2024 pm 01:10 PM
Laut Nachrichten dieser Website vom 22. Juli entdeckten ausländische Medien, Twistedvoxel, den gemunkelten PS5-Entwicklungscodenamen „Trinity“ und zugehörige Konfigurationsdateien für die Bildqualität im neuesten „World Part 1“-Updatecode von „No Man’s Sky“, was beweist, dass Sony es ist voraussichtlich Das PS5Pro-Modell wurde kürzlich auf den Markt gebracht. Obwohl „No Man’s Sky“ in den letzten Updates die Grafikleistung des Spiels verbessert hat, glauben viele Spieler immer noch, dass HelloGames den Weg für neue Modelle ebnen könnte. Laut den neuesten Grafikvoreinstellungen wird die dynamische Auflösung des Spiels unter PS5 Pro steigen Die Skalierung wurde von 0,6 auf 0,8 erhöht, was bedeutet, dass das Spiel eine höhere durchschnittliche Auflösung hat und einige grafische Details von „Hoch“ auf „Ultra“ angehoben wurden, aber seit jedem Spiel
 Erklärung zum Aktivieren der Mikrofonberechtigung für Apple-Handyspiele
Mar 22, 2024 pm 05:56 PM
Erklärung zum Aktivieren der Mikrofonberechtigung für Apple-Handyspiele
Mar 22, 2024 pm 05:56 PM
1. Klicken Sie in den Telefoneinstellungen auf [Datenschutz]. 2. Klicken Sie auf die Option [Mikrofon]. 3. Schalten Sie den Schalter auf der rechten Seite der Spielanwendung ein, der das Festlegen von Mikrofonberechtigungen erfordert.
 So lösen Sie das Problem, dass die Taskleiste beim Spielen unter WIN10 immer wieder angezeigt wird_So lösen Sie das Problem, dass die Taskleiste beim Spielen unter WIN10 immer wieder angezeigt wird
Mar 28, 2024 am 08:36 AM
So lösen Sie das Problem, dass die Taskleiste beim Spielen unter WIN10 immer wieder angezeigt wird_So lösen Sie das Problem, dass die Taskleiste beim Spielen unter WIN10 immer wieder angezeigt wird
Mar 28, 2024 am 08:36 AM
1. Klicken Sie mit der rechten Maustaste auf eine leere Stelle in der Taskleiste, suchen Sie dann nach „Eigenschaften“ und klicken Sie darauf. 2. Hier sehen Sie, dass die Systemstandardeinstellung nicht über die Option zum automatischen Ausblenden der Taskleiste verfügt. 3. Klicken Sie zum Überprüfen und dann auf OK, um die Änderungen zu speichern. 4. Wenn wir zu unserem Desktop zurückkehren, können wir sehen, dass die Taskleiste automatisch ausgeblendet wird. Wenn wir den Mauszeiger nach unten bewegen, wird sie wieder angezeigt.




