 Backend-Entwicklung
Backend-Entwicklung
 C++
C++
 Verwenden Sie Addition oder Subtraktion, um die minimale Anzahl von Schritten für N bei jedem Schritt zu erhalten
Verwenden Sie Addition oder Subtraktion, um die minimale Anzahl von Schritten für N bei jedem Schritt zu erhalten
Verwenden Sie Addition oder Subtraktion, um die minimale Anzahl von Schritten für N bei jedem Schritt zu erhalten
Aus der obigen Problemstellung besteht unsere Aufgabe darin, die Mindestanzahl von Schritten zu ermitteln, in denen wir durch Addition oder Subtraktion jeweils die gegebene Zahl N erhalten können. Wir können verstehen, dass wir die Mindestanzahl der Schritte, die ausgeführt werden können, und die Reihenfolge der Schritte für jede gegebene ganze Zahl N ausdrucken müssen, indem wir die Schrittnummern addieren und subtrahieren, um eine Zahl beginnend bei 0 zu erhalten.
In diesem Aufgabensatz können wir bei jedem Schritt eine Zahl addieren oder subtrahieren, die der Anzahl der Schritte zur aktuellen Position entspricht. Beispielsweise können wir in Schritt 1 1 oder -1 hinzufügen. Außerdem können wir in Schritt 2 2 oder -2 hinzufügen und so weiter. Je nach Situation können wir bei jedem Schritt Zahlen addieren oder subtrahieren.
Die größte Herausforderung dieses Problems besteht darin, dass wir die Mindestanzahl an Schritten beginnend bei 0 ausführen müssen, um N zu erreichen. Lassen Sie uns dieses Problem anhand eines Beispiels besser verstehen.
Das unten angegebene Beispiel zeigt Ihnen jede Zahl, die wir in zwei Schritten beginnend bei 0 erhalten können, indem wir die oben genannten Operationen ausführen.
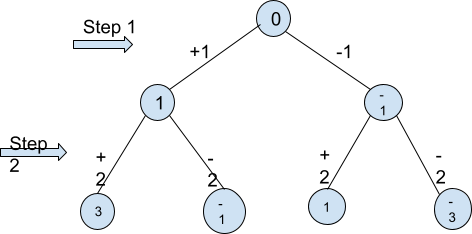
Angenommen, wir haben N=1.
Ausgabe
Minimum no of steps: 1 Sequence of steps: 1
Anleitung
Wir können 1 auf zwei Arten erreichen –
Fügen Sie einfach 1 zu Schritt 1 hinzu, um von 0 auf 1 zu gelangen, was 1 Schritt dauert.
Subtrahieren Sie 1 in Schritt 1, um von 0 auf -1 zu gelangen, und addieren Sie dann 2 in Schritt 2, um von -1 auf 1 zu gelangen, was 2 Schritte dauert.
Da die Frage besagt, dass wir die Mindestanzahl an Schritten benötigen, um eine beliebige Zahl N zu erreichen, ist die gewünschte Ausgabe für diese Eingabe 1.
Für N=3
Ausgabe
Minimum no of steps: 2 Sequence of steps: 1 2
Anleitung
Wir addieren 1 in Schritt 1, um von 0 auf 1 zu gelangen, und fügen dann 2 in Schritt 2 hinzu, um von 1 auf 3 zu gelangen.
Methode
Der beste Weg, das Problem zu lösen, besteht darin, zunächst herauszufinden, ob N positiv oder negativ ist. Wir müssen die entsprechende Anzahl an Schritten addieren bzw. subtrahieren, um das Problem zu lösen.
Wenn N eine positive Zahl ist, füge weitere Schritte hinzu, bis die Summe größer oder gleich N ist.
Wenn N negativ ist, subtrahieren Sie die Anzahl der Schritte entsprechend weiter, bis die Summe größer oder gleich N ist.
Wenn die Summe im obigen Fall gleich N ist, geben Sie die Anzahl der Schritte und die Reihenfolge der Schritte zurück. Das Hauptproblem besteht darin, mit der Situation umzugehen, wenn N überschritten wird.
Sobald die Summe N überschreitet, prüfen Sie, ob (Summe-N) gerade oder ungerade ist.
Wenn (Summe-N) gerade ist, müssen wir die Subtraktion in Schritten von (Summe-N)/2 durchführen, um N zu erhalten.
Lassen Sie uns diesen Fall anhand eines geeigneten Beispiels besser verstehen.
Für N=8
1+2+3+4=10, also mehr als 8.
Weil 10-8=2 eine gerade Zahl ist. Wir subtrahieren also in Schritten von 2/2, also
Schritt 1. Die Reihenfolge der Schritte ist also -1 2 3 4 und das Minimum
Die Anzahl der Schritte, um N zu erreichen, beträgt 4.
Wenn (Summe-N) eine ungerade Zahl ist, bestimmen Sie zunächst, ob die Zahl, deren Summe im vorherigen Schritt N überschreitet, gerade oder ungerade ist.
Wenn der vorherige Schritt ungerade war, führen Sie einen Schritt aus, indem Sie die nächste Schrittnummer hinzufügen, wodurch unsere (Summe-N) gerade wird, und führen Sie dann die oben genannten Schritte aus, um das gewünschte Ergebnis zu erhalten.
Zum Beispiel N=9
1+2+3+4=10, was mehr als 9 ist.
Weil 10-9=1 ist, ist dies eine ungerade Zahl. Der nächste Schritt ist 5, was eine ungerade Zahl ist, also machen wir einfach einen Schritt und addieren 5 zur Summe, um 15 zu erhalten, was (Summe-N)=6 ergibt. Wenn Sie die Subtraktion in Schritt 3 durchführen, erhalten Sie die Sequenz 1 2 -3 4 5, die die gewünschte Ausgabe darstellt.
Angenommen, der vorherige Schritt ist eine gerade Zahl. In diesem Fall müssen wir zwei Schritte ausführen, den i-ten Schritt addieren und den (i+1) Schritt subtrahieren, um (Summe-N) als gerade Zahl zu erhalten die gewünschte Schrittfolge.
Für N=5
1+2+3=6, mehr als 5.
Da (sum-N) =1, betrachten wir den letzten Schritt, wenn su die Zahl N überschreitet. Da es sich um eine gerade Zahl handelt, führen wir zwei Schritte aus, Schritt 4 und Schritt 5. Unsere Aufgabe besteht darin, (Summe-N) gleichmäßig zu machen. Indem wir in Schritt 4 addieren und in Schritt 5 subtrahieren, können wir (Summe-N) erhalten, selbst wenn 1 von der Summe subtrahiert wird. Da (Summe-N) gleich 0 ist, erhalten wir N. Daher ist die Reihenfolge 1 2 3 4 -5.
Beispiel
Hier ist der C++-Code für die Methode -
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void minimumStep(int n){
vector <int> steps; // for storing the sequence
int totalSum=0;
int temp=0;
if(n>=0){ // if n is positive then temp will store positive
temp=1;
} else {
temp=-1; // n is negative then temp will store negative
}
n=abs(n);
int step=0;
for(step=1;totalSum<n;step++){ // for storing the steps till sum is not greater than n
steps.push_back(temp*step);
totalSum=totalSum+step;
}
if(totalSum>temp*n) { //when sum greater than n
if(step%2==0) { //when step is even
totalSum=totalSum-n;
if((totalSum)%2!=0) { // when totalSum-n is odd
steps.push_back(temp*step); //store the addition of next step
steps.push_back((temp*-1)*(step+1)); // store the subtraction of next step
totalSum--; //make totalSum even
}
int check=(totalSum)/2;
check--;
steps[check]=steps[check]*-1;
} else { //when step is odd
totalSum=totalSum-n;
if((totalSum)%2!=0) { // when totalSum-n is odd
steps.push_back(temp*step); //store the next addition value
totalSum+=step;
step++;
}
int check=(totalSum)/2;
check--;
steps[check]=steps[check]*-1;
}
}
//print the minimum number of steps taken
cout<<"The minimum number of steps : "<<steps.size()<<endl;
//print the steps is stored in vector
cout<<"Sequence of steps : ";
for(int i=0;i<steps.size();i++){
cout<<steps[i]<<" ";
}
}
int main(){
int m=17;
minimumStep(m);
return 0;
}
Ausgabe
The minimum number of steps : 6 Sequence of steps : 1 -2 3 4 5 6
Zeitliche Komplexität: O(sqrt(N))
Raumkomplexität: O(sqrt(N))
Fazit
In diesem Artikel versuchen wir, die Methode zu erklären, mit der man die Mindestanzahl an Schritten ermittelt, um N zu erreichen, indem man bei jedem Schritt addiert oder subtrahiert und die Sequenz ausgibt. Ich hoffe, dass dieser Artikel Ihnen hilft, dieses Konzept besser kennenzulernen.
Das obige ist der detaillierte Inhalt vonVerwenden Sie Addition oder Subtraktion, um die minimale Anzahl von Schritten für N bei jedem Schritt zu erhalten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 So schreiben Sie Python-Additionscode_Tutorial zum Schreiben von Python-Additionscode
Apr 02, 2024 pm 06:16 PM
So schreiben Sie Python-Additionscode_Tutorial zum Schreiben von Python-Additionscode
Apr 02, 2024 pm 06:16 PM
1. Öffnen Sie zunächst die Online-Python-Bearbeitungsseite. 2. Anschließend geben Sie im Programmbereich den Programmcode ein. 3. Klicken Sie dann oben links auf „Ausführen“, geben Sie den ersten Summanden ein, drücken Sie die Eingabetaste und geben Sie den zweiten Summanden ein. 4. Drücken Sie abschließend die Eingabetaste, um die Summe der beiden Summanden zu erhalten. Dies ist ein einfacher Python-Zusatzcode.
 Dividieren Sie zwei ganze Zahlen, ohne die Multiplikations-, Divisions- und Modulo-Operatoren zu verwenden
Sep 21, 2023 pm 12:41 PM
Dividieren Sie zwei ganze Zahlen, ohne die Multiplikations-, Divisions- und Modulo-Operatoren zu verwenden
Sep 21, 2023 pm 12:41 PM
Bei diesem Problem müssen wir nur zwei ganze Zahlen dividieren, ohne Multiplikations-, Divisions- und Modulo-Operatoren zu verwenden. Obwohl wir Additions-, Multiplikations- oder Bitoperationen verwenden können. Die Problemstellung besagt, dass wir zwei ganze Zahlen x und y erhalten. Ohne Multiplikation, Division oder den Modulo-Operator müssen wir den Quotienten von x dividiert durch y bestimmen. Beispiel Eingabe: x=15, y=5 Ausgabe: 3 Eingabe: x=10, y=4 Ausgabe: 2 Eingabe: x=-20, y=3 Ausgabe: -6 Methode Methode 1 (verwenden Sie einfache Mathematik) hier Als Methode verwenden wir einen einfachen mathematischen Algorithmus. Hier ist eine Schritt-für-Schritt-Erklärung der Schritte, die wir befolgen werden – wir werden den Divisor (d. h. y) so lange vom Dividenden (d. h. x) subtrahieren, bis x größer oder gleich y ist. wenn y größer als x ist
 Kenntnisse im Betrieb von Oracle-Datenbanken: Detaillierte Erläuterung des Subtraktionsvorgangs
Mar 02, 2024 pm 06:15 PM
Kenntnisse im Betrieb von Oracle-Datenbanken: Detaillierte Erläuterung des Subtraktionsvorgangs
Mar 02, 2024 pm 06:15 PM
Als leistungsstarkes relationales Datenbankverwaltungssystem bietet die Oracle-Datenbank eine Fülle von Rechenoperationen, um den Benutzeranforderungen gerecht zu werden. Im täglichen Datenbankbetrieb ist die Subtraktionsoperation eine häufige und wichtige Operation. Sie kann uns dabei helfen, die Subtraktionsoperation von Daten zu realisieren, um die benötigten Ergebnisse zu erhalten. In diesem Artikel werden die Techniken im Zusammenhang mit Subtraktionsoperationen in der Oracle-Datenbank ausführlich erläutert und spezifische Codebeispiele gegeben, um den Lesern zu helfen, diese Funktion besser zu verstehen und zu verwenden. 1. Grundkonzepte von Subtraktionsoperationen in Oracle-Daten
 So führen Sie eine Subtraktion in Excel durch
Mar 20, 2024 pm 02:46 PM
So führen Sie eine Subtraktion in Excel durch
Mar 20, 2024 pm 02:46 PM
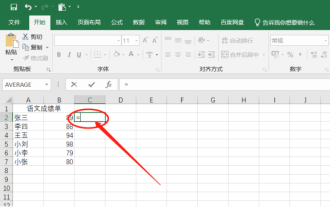
Excel ist eine unverzichtbare Bürosoftware in unserem täglichen Büro, daher werden einige Leute, die Excel zum ersten Mal lernen, immer auf einige kleine Probleme stoßen, wie zum Beispiel, wie man in Excel subtrahiert. Heute werde ich mit meinen Freunden sprechen. Teilen Sie dies Die einzelnen Bedienungsschritte finden Sie unten. Freunde, schauen Sie sich das genauer an! 1. Öffnen Sie zunächst das Excel-Datenblatt. Excel möchte die Subtraktion über Formeln durchführen, und Formeln orientieren sich im Allgemeinen am Gleichheitszeichen. Geben Sie daher in den Zellen, die subtrahiert werden müssen, zunächst = ein (wie unten rot dargestellt). Teil gezeigt). 2. Klicken Sie dann auf die Zelle, in der sich der Minuend befindet. Der Name der Zelle wird automatisch zur Formel hinzugefügt (wie im roten Kreis in der Abbildung unten dargestellt). 3
 Entdecken Sie die Bedeutung und Anwendung von Python-Operatoren: Addition, Subtraktion, Multiplikation und Division
Jan 20, 2024 am 09:21 AM
Entdecken Sie die Bedeutung und Anwendung von Python-Operatoren: Addition, Subtraktion, Multiplikation und Division
Jan 20, 2024 am 09:21 AM
Ein tiefgreifendes Verständnis der Python-Operatoren: Addition, Subtraktion, Multiplikation, Division und ihrer Bedeutung erfordert spezifische Codebeispiele. In der Programmiersprache Python sind Operatoren eines der wichtigen Werkzeuge zur Durchführung verschiedener mathematischer Operationen. Unter ihnen sind Addition, Subtraktion, Multiplikation und Division die gebräuchlichsten Operatoren. In diesem Artikel wird die Bedeutung dieser Operatoren und ihre Verwendung in Python erläutert. Additionsoperator (+) Der Additionsoperator wird zum Addieren zweier Zahlen verwendet und kann auch zum Verketten zweier Zeichenfolgen verwendet werden. x=5y=3Ergebnis
 So erstellen Sie subtraktives Design und verschönern Diagramme in PPT
Mar 20, 2024 pm 02:00 PM
So erstellen Sie subtraktives Design und verschönern Diagramme in PPT
Mar 20, 2024 pm 02:00 PM
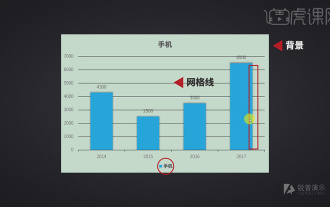
1. Der grundlegende Verschönerungsoperationsraum von Diagrammen ist klein und störende Anzeigeelemente werden entfernt. Zu den Elementen, die die Daten beeinträchtigen, gehören Hintergrund, Rasterlinien und Legenden. Sie können gelöscht, verschönert und Schatten abgemildert werden. 2. Geben Sie [PPT] ein, [Öffnen] Diagramm, klicken Sie auf [Diagramm], wählen Sie [+] und deaktivieren Sie es, wie in der Abbildung gezeigt. 3. [Rechtsklick], um das Format der Datenreihe festzulegen, klicken Sie auf [Füllen] und aktivieren Sie [Keine Füllung]. Klicken Sie auf [Datenspalte], klicken Sie auf [Schatten], um den Schatten zu entfernen, wählen Sie [Umriss] und färben Sie [Text] weiß. 4. Klicken Sie auf [Skalierung], wählen Sie [Skalenmarkierung] und passen Sie [Thementyp] Keine, [Farbe] Weiß an, wie in der Abbildung gezeigt. 5. Löschen Sie die Stellen, die gelöscht werden müssen, um die Tabelle übersichtlicher zu gestalten. Fügen Sie beim Entwerfen nicht blind Dinge hinzu, sondern gehen Sie entsprechend vor.
 Verwenden Sie pthread, um Matrixaddition und -subtraktion in C/C++ zu implementieren
Aug 28, 2023 am 09:05 AM
Verwenden Sie pthread, um Matrixaddition und -subtraktion in C/C++ zu implementieren
Aug 28, 2023 am 09:05 AM
Hier erfahren Sie, wie Sie eine Matrixaddition und -subtraktion in einer Multithread-Umgebung durchführen. pthread wird verwendet, um mehrere Threads gleichzeitig in C oder C++ auszuführen. Es gibt zwei Matrizen A und B. Die Reihenfolge jeder Matrix ist (mxn). Jeder Thread erhält jede Zeile und führt eine Addition oder Subtraktion durch. Für m Zeilen gibt es also m verschiedene Threads. Beispiel#include<iostream>#include<pthread.h>#include<cstdlib>#include<cstdint>#defineCORE3#defineMAX3usingnamespacestd;i
 C-Programm zur Addition und Multiplikation mit bitweisen Operationen
Sep 16, 2023 pm 07:49 PM
C-Programm zur Addition und Multiplikation mit bitweisen Operationen
Sep 16, 2023 pm 07:49 PM
Bitweise Operatoren operieren mit Bits (d. h. operieren mit dem Binärwert des Operanden) Operator Beschreibung & Bitweises ODER | aba^b000011101110 Beispiel Das Folgende ist ein C-Programm für Addition und Multiplikation 2 mit Hilfe von bitweisen Operatoren – Live-Demonstration #include<stdio.h>main(){ inta;



