 Backend-Entwicklung
Backend-Entwicklung
 C++
C++
 C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird
C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird
C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird

Hyperbolische Funktionen werden mithilfe von Hyperbeln anstelle von Kreisen definiert und entsprechen gewöhnlichen trigonometrischen Funktionen. Es gibt den Verhältnisparameter in der hyperbolischen Sinusfunktion aus dem angegebenen Winkel im Bogenmaß zurück. Aber machen Sie das Gegenteil, oder anders gesagt. Wenn wir einen Winkel aus einem hyperbolischen Sinus berechnen wollen, benötigen wir eine umgekehrte hyperbolische trigonometrische Operation wie die hyperbolische Umkehrsinusoperation.
In diesem Kurs wird gezeigt, wie Sie die hyperbolische Umkehrsinusfunktion (asinh) in C++ verwenden, um Winkel mithilfe des hyperbolischen Sinuswerts im Bogenmaß zu berechnen. Die Operation des hyperbolischen Arkussinus folgt der folgenden Formel -
$$mathrm{sinh^{-1}x:=:In(x:+:sqrt{x^2:+:1})}, wobei:In:is:natürlicher Logarithmus:(log_e : k)$ $
asinh()-Funktion
Basierend auf dem Hyperbelsinus kann der Winkel mit der Funktion asinh() berechnet werden. Diese Funktion ist in der C++-Standardbibliothek enthalten. Bevor wir diese Funktion verwenden, müssen wir die cmath-Bibliothek importieren. Diese Methode gibt den Winkel im Bogenmaß zurück und verwendet den Sinuswert als Argument. Im Folgenden wird eine einfache Syntax verwendet -
Grammatik
#include < cmath > asinh( <hyperbolic sine value> )
Algorithmus
- Nehmen Sie den hyperbolischen Sinuswert x als Eingabe
- Verwenden Sie asinh(x), um sinh−1(x) zu berechnen
- Ergebnisse zurückgeben.
Beispiel
#include <iostream>
#include <cmath>
using namespace std;
float solve( float x ) {
float answer;
answer = asinh( x );
return answer;
}
int main()
{
float angle, ang_deg;
angle = solve( 2.3013 );
ang_deg = angle * 180 / 3.14159;
cout << "The angle (in radian) for given hyperbolic sine value 2.3013 is: " << angle << " = " << ang_deg << " (in degrees)" << endl;
angle = solve( 11.5487 );
ang_deg = angle * 180 / 3.14159;
cout << "The angle (in radian) for given hyperbolic sine value 11.5487 is: " << angle << " = " << ang_deg << " (in degrees)" << endl;
angle = solve( 0.86867 );
ang_deg = angle * 180 / 3.14159;
cout << "The angle (in radian) for given hyperbolic sine value 0.86867 is: " << angle << " = " << ang_deg << " (in degrees)" << endl;
angle = solve( -0.86867 );
ang_deg = angle * 180 / 3.14159;
cout << "The angle (in radian) for given hyperbolic sine value - 0.86867 is: " << angle << " = " << ang_deg << " (in degrees)" << endl;
}
Ausgabe
The angle (in radian) for given hyperbolic sine value 2.3013 is: 1.5708 = 90.0001 (in degrees) The angle (in radian) for given hyperbolic sine value 11.5487 is: 3.14159 = 180 (in degrees) The angle (in radian) for given hyperbolic sine value 0.86867 is: 0.785397 = 45 (in degrees) The angle (in radian) for given hyperbolic sine value - 0.86867 is: -0.785397 = -45 (in degrees)
asinh() empfängt in diesem Fall den hyperbolischen Sinuswert und gibt den Winkel im Bogenmaßformat zurück. Wir konvertieren diese Ausgabe mithilfe der folgenden Formel vom Bogenmaß in Grad.
$$mathrm{theta_{deg}:=:theta_{rad}:timesfrac{180}{pi}}$$
Fazit
Um inverse hyperbolische Operationen mit Sinuswerten durchzuführen, verwenden wir die Funktion asinh() aus dem cmath-Paket. Nachdem die Funktion einen hyperbolischen Sinuswert als Eingabe erhalten hat, gibt sie den gewünschten Winkel im Bogenmaß aus. In älteren Versionen von C und C++ ist der Rückgabetyp double; spätere Versionen von C++ verwenden auch überladene Formen von float und long-double. Wenn ein ganzzahliger Wert als Argument übergeben wird, wird die Funktion asinh() aufgerufen, nachdem das Eingabeargument in den Typ double konvertiert wurde.
Das obige ist der detaillierte Inhalt vonC++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 i9-12900H Parameterbewertungsliste
Feb 23, 2024 am 09:25 AM
i9-12900H Parameterbewertungsliste
Feb 23, 2024 am 09:25 AM
Der i9-12900H ist ein 14-Kern-Prozessor und die Threads sind ebenfalls sehr hoch. Einige Parameter wurden verbessert und können den Benutzern ein hervorragendes Erlebnis bieten . Überprüfung der Parameterbewertung des i9-12900H: 1. Der i9-12900H ist ein 14-Kern-Prozessor, der die q1-Architektur und die 24576-KB-Prozesstechnologie übernimmt und auf 20 Threads aktualisiert wurde. 2. Die maximale CPU-Frequenz beträgt 1,80! 5,00 GHz, was hauptsächlich von der Arbeitslast abhängt. 3. Im Vergleich zum Preis ist es sehr gut geeignet. Das Preis-Leistungs-Verhältnis ist sehr gut und für einige Partner, die eine normale Nutzung benötigen, sehr gut geeignet. i9-12900H Parameterbewertung und Leistungsbenchmarks
 Sicherheitsüberprüfung des C++-Funktionsparametertyps
Apr 19, 2024 pm 12:00 PM
Sicherheitsüberprüfung des C++-Funktionsparametertyps
Apr 19, 2024 pm 12:00 PM
Die Sicherheitsüberprüfung von C++-Parametertypen stellt durch Überprüfungen zur Kompilierungszeit, Laufzeitüberprüfungen und statischen Behauptungen sicher, dass Funktionen nur Werte erwarteter Typen akzeptieren, wodurch unerwartetes Verhalten und Programmabstürze verhindert werden: Typüberprüfung zur Kompilierungszeit: Der Compiler überprüft die Typkompatibilität. Überprüfung des Laufzeittyps: Verwenden Sie Dynamic_cast, um die Typkompatibilität zu überprüfen und eine Ausnahme auszulösen, wenn keine Übereinstimmung vorliegt. Statische Behauptung: Typbedingungen zur Kompilierzeit geltend machen.
 C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird
Sep 17, 2023 am 10:49 AM
C++-Programm zum Ermitteln des Werts der Umkehrfunktion des hyperbolischen Sinus, wobei ein gegebener Wert als Argument verwendet wird
Sep 17, 2023 am 10:49 AM
Hyperbelfunktionen werden mithilfe von Hyperbeln anstelle von Kreisen definiert und entsprechen gewöhnlichen trigonometrischen Funktionen. Es gibt den Verhältnisparameter in der hyperbolischen Sinusfunktion aus dem angegebenen Winkel im Bogenmaß zurück. Aber machen Sie das Gegenteil, oder anders gesagt. Wenn wir einen Winkel aus einem hyperbolischen Sinus berechnen wollen, benötigen wir eine umgekehrte hyperbolische trigonometrische Operation wie die hyperbolische Umkehrsinusoperation. In diesem Kurs wird gezeigt, wie Sie die hyperbolische Umkehrsinusfunktion (asinh) in C++ verwenden, um Winkel mithilfe des hyperbolischen Sinuswerts im Bogenmaß zu berechnen. Die hyperbolische Arkussinusoperation folgt der folgenden Formel -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Wo\:In\:ist\:natürlicher Logarithmus\:(log_e\:k)
 Das C-Programm verwendet die Funktion rename(), um den Dateinamen zu ändern
Sep 21, 2023 pm 10:01 PM
Das C-Programm verwendet die Funktion rename(), um den Dateinamen zu ändern
Sep 21, 2023 pm 10:01 PM
Die Umbenennungsfunktion ändert den alten Namen einer Datei oder eines Verzeichnisses in den neuen Namen. Dieser Vorgang ähnelt dem Verschiebevorgang. Wir können diese Umbenennungsfunktion also auch zum Verschieben von Dateien verwenden. Diese Funktion ist in der Headerdatei der stdio.h-Bibliothek vorhanden. Die Syntax der Umbenennungsfunktion lautet wie folgt: intrename(constchar*oldname,constchar*newname); Die Funktion der rename()-Funktion akzeptiert zwei Parameter. Einer ist alter Name und der andere ist neuer Name. Beide Parameter sind Zeiger auf konstante Zeichen, die den alten und neuen Namen der Datei definieren. Gibt Null zurück, wenn die Datei erfolgreich umbenannt wurde; andernfalls wird eine Ganzzahl ungleich Null zurückgegeben. Während eines Umbenennungsvorgangs
 C++-Programm zum Drucken eines Wörterbuchs
Sep 11, 2023 am 10:33 AM
C++-Programm zum Drucken eines Wörterbuchs
Sep 11, 2023 am 10:33 AM
Eine Karte ist ein spezieller Containertyp in C++, bei dem jedes Element ein Paar aus zwei Werten ist, nämlich einem Schlüsselwert und einem zugeordneten Wert. Der Schlüsselwert wird zum Indizieren jedes Elements verwendet, und der zugeordnete Wert ist der mit dem Schlüssel verknüpfte Wert. Unabhängig davon, ob der zugeordnete Wert eindeutig ist, ist der Schlüssel immer eindeutig. Um Kartenelemente in C++ zu drucken, müssen wir einen Iterator verwenden. Ein Element in einer Menge von Elementen wird durch ein Iteratorobjekt angegeben. Iteratoren werden hauptsächlich mit Arrays und anderen Arten von Containern (z. B. Vektoren) verwendet und verfügen über einen bestimmten Satz von Operationen, mit denen bestimmte Elemente innerhalb eines bestimmten Bereichs identifiziert werden können. Iteratoren können inkrementiert oder dekrementiert werden, um auf verschiedene Elemente in einem Bereich oder Container zu verweisen. Der Iterator zeigt auf den Speicherort eines bestimmten Elements im Bereich. Drucken einer Karte in C++ mit Iteratoren Schauen wir uns zunächst an, wie man definiert
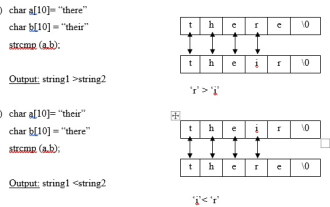 Schreiben Sie ein C-Programm, das die Bibliotheksfunktion strncmp verwendet, um zwei Zeichenfolgen zu vergleichen
Sep 09, 2023 pm 01:17 PM
Schreiben Sie ein C-Programm, das die Bibliotheksfunktion strncmp verwendet, um zwei Zeichenfolgen zu vergleichen
Sep 09, 2023 pm 01:17 PM
Strncmp ist eine vordefinierte Bibliotheksfunktion, die in der Datei string.h vorhanden ist und zum Vergleichen zweier Zeichenfolgen und zum Anzeigen der größeren Zeichenfolge verwendet wird. strcmp-Funktion (String-Vergleich) Diese Funktion vergleicht zwei Strings. Es gibt die ASCII-Differenz des ersten nicht übereinstimmenden Zeichens in den beiden Zeichenfolgen zurück. Syntax intstrcmp(string1,string2); Wenn die Differenz gleich Null ist, dann ist string1=string2. Wenn die Differenz positiv ist, ist string1>string2. Wenn die Differenz negativ ist, ist string1<string2. Beispiel für eine strncmp-Funktion Diese Funktion wird verwendet, um die ersten n Zeichen zweier Zeichenfolgen zu vergleichen. Syntaxstrn
 C++-Programm zum Überprüfen, ob ein Zeichen alphabetisch oder nicht alphabetisch ist
Sep 14, 2023 pm 03:37 PM
C++-Programm zum Überprüfen, ob ein Zeichen alphabetisch oder nicht alphabetisch ist
Sep 14, 2023 pm 03:37 PM
Die Verwendung von Zeichenfolgen oder Zeichen ist manchmal sehr nützlich, wenn man einige Probleme der Logikprogrammierung löst. Eine Zeichenfolge ist eine Sammlung von Zeichen. Dabei handelt es sich um einen 1-Byte-Datentyp, der zum Speichern von Symbolen in ASCII-Werten verwendet wird. Symbole können englische Buchstaben, Zahlen oder Sonderzeichen sein. In diesem Artikel erfahren Sie, wie Sie mit C++ überprüfen, ob ein Zeichen ein englischer Buchstabe oder ein Buchstabe des Alphabets ist. Überprüfen der Funktion isalpha() Um zu überprüfen, ob eine Zahl ein Buchstabe ist, können wir die Funktion isalpha() in der Header-Datei ctype.h verwenden. Dies nimmt ein Zeichen als Eingabe und gibt „true“ zurück, wenn es sich um ein Alphabet handelt, andernfalls „false“. Schauen wir uns die folgende C++-Implementierung an, um die Verwendung dieser Funktion zu verstehen. Die chinesische Übersetzung von Beispiel lautet: show
 Erweiterte Verwendung von Referenzparametern und Zeigerparametern in C++-Funktionen
Apr 21, 2024 am 09:39 AM
Erweiterte Verwendung von Referenzparametern und Zeigerparametern in C++-Funktionen
Apr 21, 2024 am 09:39 AM
Referenzparameter in C++-Funktionen (im Wesentlichen Variablenaliase; durch Ändern der Referenz wird die Originalvariable geändert) und Zeigerparameter (Speichern der Speicheradresse der Originalvariablen, Ändern der Variablen durch Dereferenzierung des Zeigers) werden beim Übergeben und Ändern von Variablen unterschiedlich verwendet. Referenzparameter werden oft verwendet, um Originalvariablen (insbesondere große Strukturen) zu ändern, um Kopieraufwand bei der Übergabe an Konstruktoren oder Zuweisungsoperatoren zu vermeiden. Zeigerparameter werden verwendet, um flexibel auf Speicherorte zu zeigen, dynamische Datenstrukturen zu implementieren oder Nullzeiger zur Darstellung optionaler Parameter zu übergeben.



