C/C++-Programm, das mit dem Merge-Sort-Algorithmus geschrieben wurde, um den umgekehrten Logarithmus in einem Array zu berechnen?

Der Umkehrzähler, der beim Sortieren eines bestimmten Arrays auftritt, wird als Umkehrzähler bezeichnet. Das inverse Problem ist ein klassisches Problem, das mit dem Merge-Sort-Algorithmus gelöst werden kann. In diesem Problem v zählen wir alle Elemente links davon, die größer als dieses sind, und addieren die Anzahl zur Ausgabe. Diese Logik wird in der Zusammenführungsfunktion der Zusammenführungssortierung vervollständigt.

Um dieses Thema besser zu verstehen, nehmen wir ein Beispiel. Betrachten wir die beiden am Zusammenführungsprozess beteiligten Unterarrays –

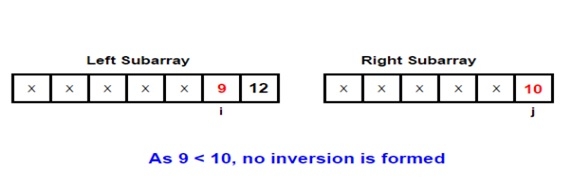
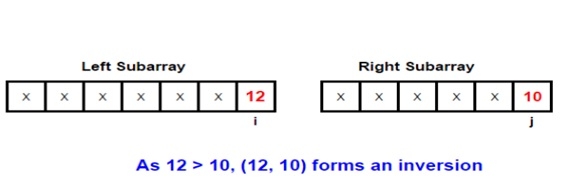
Input: arr[] = { 1, 9, 6, 4, 5}
Output: Inversion count is 5

Erklärung

Anzahl der Inversionen eines Arrays

Bestimmen Sie bei einem gegebenen Array seine Umkehrung Anzahl der Umdrehungen. Wenn (i < j) und (A[i] > A[j]), dann wird das Paar (i, j) als Inversion des Arrays A bezeichnet. Wir müssen alle derartigen Paare in arr

< p> zählen. Beispielsweise gibt es 5 Inversionen im

-Array

(9,6), (9,4), (9,5), (6,4), (6 ,5)

1. Vergleichen Sie die Werte der Elemente miteinander.

2. Wenn der Wert am unteren Index höher ist, erhöhen Sie den Zähler.

3. Zeigen Sie die Ergebnisse an.

Beispiel

#include <stdio.h>
int Merge(int arr[], int aux[], int low, int mid, int high) {
   int k = low, i = low, j = mid + 1;
   int inversionCount = 0;
   while (i <= mid && j <= high) {
      if (arr[i] <= arr[j]) {
         aux[k++] = arr[i++];
      } else {
         aux[k++] = arr[j++];
         inversionCount += (mid - i + 1); // NOTE
      }
   }
   while (i <= mid)
   aux[k++] = arr[i++];
   for (int i = low; i <= high; i++)
      arr[i] = aux[i];
   return inversionCount;
}
int MergeSort(int arr[], int aux[], int low, int high) {
   if (high == low) // if run size == 1
      return 0;
   int mid = (low + ((high - low) >> 1));
   int inversionCount = 0;
   inversionCount += MergeSort(arr, aux, low, mid);
   inversionCount += MergeSort(arr, aux, mid + 1, high);
   inversionCount += Merge(arr, aux, low, mid, high);
   return inversionCount;
}
int main() {
   int arr[] = { 1, 9, 6, 4, 5 };
   int N = 5;
   int aux[N];
   for (int i = 0; i < N; i++)
      aux[i] = arr[i];
   printf("Inversion count is %d", MergeSort(arr, aux, 0, N - 1));
   return 0;
}

Das obige ist der detaillierte Inhalt vonC/C++-Programm, das mit dem Merge-Sort-Algorithmus geschrieben wurde, um den umgekehrten Logarithmus in einem Array zu berechnen?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!