 Backend-Entwicklung
Backend-Entwicklung
 PHP-Tutorial
PHP-Tutorial
 Forschung zu Anwendungsszenarien und Implementierungsmethoden des topologischen Sortieralgorithmus in PHP.
Forschung zu Anwendungsszenarien und Implementierungsmethoden des topologischen Sortieralgorithmus in PHP.
Forschung zu Anwendungsszenarien und Implementierungsmethoden des topologischen Sortieralgorithmus in PHP.

Untersuchung der Anwendungsszenarien und Implementierungsmethoden des topologischen Sortieralgorithmus in PHP
In der Informatik ist topologische Sortierung ein Algorithmus zum Sortieren von Knoten in einem gerichteten azyklischen Graphen. Dieser Algorithmus kann zur Lösung von Problemen in einigen praktischen Szenarien verwendet werden, z. B. bei der Aufgabenplanung, der Abhängigkeitsanalyse usw. In diesem Artikel werden die Anwendungsszenarien des topologischen Sortieralgorithmus in PHP untersucht und spezifische Implementierungsmethoden und Codebeispiele vorgestellt.
1. Anwendungsszenarien der topologischen Sortierung
In vielen praktischen Szenarien stehen wir häufig vor der Notwendigkeit, eine Reihe von Aufgaben oder Ereignissen zu sortieren. Zwischen diesen Aufgaben bzw. Ereignissen besteht eine „Abhängigkeit“, d. h. einige Aufgaben müssen abgeschlossen sein, bevor andere Aufgaben ausgeführt werden können. Dabei handelt es sich um das Anwendungsszenario der topologischen Sortierung.
- Aufgabenplanung: In einem Aufgabenplanungssystem gibt es eine große Anzahl von Aufgaben, die in einer bestimmten Reihenfolge ausgeführt werden müssen. Einige Aufgaben hängen möglicherweise von den Ergebnissen anderer Aufgaben ab und müssen auf den Abschluss anderer Aufgaben warten, bevor sie ausgeführt werden können. Durch topologische Sortierung kann die Ausführungsreihenfolge von Aufgaben bestimmt und so die Aufgabenplanungsfunktion realisiert werden.
- Abhängigkeitsanalyse: In der Softwareentwicklung gibt es häufig Abhängigkeiten zwischen einigen Modulen oder Klassen. Durch topologische Sortierung können diese Abhängigkeiten analysiert und die Abhängigkeitsketten von Modulen oder Klassen für eine bessere Codeorganisation und -verwaltung gefunden werden.
- Kursplan: Im Stundenplan der Schule gibt es oft einige Kurse, die sequentielle Abhängigkeiten aufweisen und in einer bestimmten Reihenfolge studiert werden müssen. Durch die topologische Sortierung lässt sich die Lernreihenfolge der Lehrveranstaltungen bestimmen und Studierende dabei unterstützen, ihre Studienplanung sinnvoll zu gestalten.
2. Implementierungsmethode der topologischen Sortierung
Es gibt viele Implementierungsmethoden des topologischen Sortieralgorithmus, von denen die am häufigsten verwendete Methode auf der Tiefensuche (DFS) basiert. Nachfolgend geben wir die Implementierungsmethode der topologischen Sortierung basierend auf DFS und das entsprechende PHP-Codebeispiel an.
- Erstellen eines gerichteten Diagramms
Zunächst müssen wir ein gerichtetes Diagramm erstellen, um die Abhängigkeiten zwischen Aufgaben oder Ereignissen darzustellen. Sie können ein Array verwenden, um einen gerichteten Graphen darzustellen. Jedes Element stellt einen Knoten dar, sein Schlüssel stellt die Nummer des Knotens dar und der Wert stellt die Menge der Knoten dar, die eine direkte Abhängigkeit vom Knoten haben.
/**
* 构建有向图
* @param array $edges 边集合
* @return array
*/
function buildGraph(array $edges): array
{
$graph = [];
foreach ($edges as $edge) {
[$from, $to] = $edge;
if (!isset($graph[$from])) {
$graph[$from] = [];
}
if (!isset($graph[$to])) {
$graph[$to] = [];
}
$graph[$from][] = $to;
}
return $graph;
}- Tiefensuche
Als nächstes verwenden wir den Tiefensuchalgorithmus, um den gerichteten Graphen zu durchlaufen und die Knoten in der Reihenfolge ihrer Vervollständigung zur Ergebnismenge hinzuzufügen. Während des Durchlaufprozesses müssen wir auch feststellen, ob ein Zyklus vorliegt, dh ob der Graph ein gerichteter azyklischer Graph ist.
/**
* 深度优先搜索
* @param array $graph 有向图
* @param array $visited 访问状态集合
* @param int $node 当前节点编号
* @param array $result 结果集合
* @return bool 是否存在环
*/
function dfs(array $graph, array &$visited, int $node, array &$result): bool
{
$visited[$node] = 1; // 标记节点为正在访问
foreach ($graph[$node] as $next) {
if ($visited[$next] == 1) {
return true; // 存在环
} elseif ($visited[$next] === 0) {
if (dfs($graph, $visited, $next, $result)) {
return true; // 存在环
}
}
}
$visited[$node] = 2; // 标记节点已访问完成
$result[] = $node; // 将节点加入结果集
return false; // 不存在环
}- Topologische Sortierung durchführen
Abschließend führen wir die Eingabefunktion der topologischen Sortierung aus und geben die Ergebnismenge in umgekehrter Reihenfolge aus, um die Ausführungsreihenfolge von Aufgaben oder Ereignissen zu erhalten.
/**
* 执行拓扑排序
* @param array $edges 边集合
* @return array 排序结果
*/
function topologicalSort(array $edges): array
{
$graph = buildGraph($edges);
$n = count($graph);
$visited = array_fill(0, $n, 0);
$result = [];
for ($i = 0; $i < $n; $i++) {
if ($visited[$i] === 0 && dfs($graph, $visited, $i, $result)) {
return []; // 存在环,排序失败
}
}
return array_reverse($result); // 返回逆序排序结果
}3. Zusammenfassung
Durch die Untersuchung dieses Artikels verstehen wir die Anwendungsszenarien und Implementierungsmethoden des topologischen Sortieralgorithmus in PHP. Topologische Sortieralgorithmen haben einen wichtigen Anwendungswert in praktischen Szenarien wie der Aufgabenplanung, der Abhängigkeitsanalyse und der Kursplanung. Durch die Implementierung des topologischen Sortieralgorithmus können wir verwandte Sortierprobleme leicht lösen und die Effizienz und Wartbarkeit des Programms verbessern. Ich hoffe, dass dieser Artikel den Lesern helfen kann, topologische Sortieralgorithmen zu verstehen und anzuwenden.
Das obige ist der detaillierte Inhalt vonForschung zu Anwendungsszenarien und Implementierungsmethoden des topologischen Sortieralgorithmus in PHP.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Komplexe experimentelle Designprobleme im zweiseitigen Markt von Kuaishou
Apr 15, 2023 pm 07:40 PM
Komplexe experimentelle Designprobleme im zweiseitigen Markt von Kuaishou
Apr 15, 2023 pm 07:40 PM
1. Hintergrund des Problems 1. Einführung in das zweiseitige Marktexperiment Der zweiseitige Markt, also eine Plattform, umfasst zwei Teilnehmer, Produzenten und Verbraucher, und beide Parteien fördern sich gegenseitig. Kuaishou hat beispielsweise einen Videoproduzenten und einen Videokonsumenten, und die beiden Identitäten können sich bis zu einem gewissen Grad überschneiden. Bilaterales Experiment ist eine experimentelle Methode, die Gruppen auf Produzenten- und Verbraucherseite vereint. Bilaterale Experimente haben folgende Vorteile: (1) Die Auswirkungen der neuen Strategie auf zwei Aspekte können gleichzeitig erfasst werden, beispielsweise Änderungen im Produkt-DAU und die Anzahl der Personen, die Werke hochladen. Bilaterale Plattformen haben oft netzwerkübergreifende Effekte, je mehr Leser es gibt, desto aktiver werden die Autoren sein, und je aktiver die Autoren sind, desto mehr Leser werden ihnen folgen. (2) Effektüberlauf und -übertragung können erkannt werden. (3) Helfen Sie uns, den Wirkungsmechanismus besser zu verstehen. Das AB-Experiment selbst kann uns nicht nur den Zusammenhang zwischen Ursache und Wirkung aufzeigen
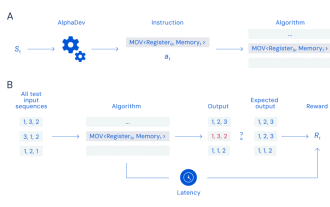 Google nutzt KI, um das Zehn-Jahres-Ranking-Algorithmus-Siegel zu brechen. Es wird jeden Tag Billionen Mal ausgeführt, aber Internetnutzer sagen, es sei die unrealistischste Forschung?
Jun 22, 2023 pm 09:18 PM
Google nutzt KI, um das Zehn-Jahres-Ranking-Algorithmus-Siegel zu brechen. Es wird jeden Tag Billionen Mal ausgeführt, aber Internetnutzer sagen, es sei die unrealistischste Forschung?
Jun 22, 2023 pm 09:18 PM
Organisieren |. Nuka-Cola, Chu Es ist eine interessante Herausforderung und es gibt viele Möglichkeiten, sie zu meistern. Es wurde viel Zeit investiert, um herauszufinden, wie Sortieraufgaben effizienter erledigt werden können. Als Grundoperation sind Sortieralgorithmen in die Standardbibliotheken der meisten Programmiersprachen integriert. Es gibt viele verschiedene Sortiertechniken und Algorithmen, die in Codebasen auf der ganzen Welt verwendet werden, um große Datenmengen online zu organisieren, aber zumindest was die mit dem LLVM-Compiler verwendeten C++-Bibliotheken betrifft, hat sich der Sortiercode seit mehr als einem Jahr nicht geändert Jahrzehnt. Kürzlich hat das Google DeepMindAI-Team nun eine entwickelt
 So filtern und sortieren Sie Daten in der Vue-Technologieentwicklung
Oct 09, 2023 pm 01:25 PM
So filtern und sortieren Sie Daten in der Vue-Technologieentwicklung
Oct 09, 2023 pm 01:25 PM
So filtern und sortieren Sie Daten in der Vue-Technologieentwicklung. In der Vue-Technologieentwicklung sind das Filtern und Sortieren von Daten sehr häufige und wichtige Funktionen. Durch Datenfilterung und -sortierung können wir die benötigten Informationen schnell abfragen und anzeigen und so die Benutzererfahrung verbessern. In diesem Artikel wird das Filtern und Sortieren von Daten in Vue vorgestellt und spezifische Codebeispiele bereitgestellt, um den Lesern zu helfen, diese Funktionen besser zu verstehen und zu verwenden. 1. Datenfilterung Datenfilterung bezieht sich auf das Herausfiltern von Daten, die den Anforderungen basierend auf bestimmten Bedingungen entsprechen. In Vue können wir comp bestehen
 Welche Sortieralgorithmen gibt es für Arrays?
Jun 02, 2024 pm 10:33 PM
Welche Sortieralgorithmen gibt es für Arrays?
Jun 02, 2024 pm 10:33 PM
Array-Sortieralgorithmen werden verwendet, um Elemente in einer bestimmten Reihenfolge anzuordnen. Zu den gängigen Arten von Algorithmen gehören: Blasensortierung: Vertauschen Sie Positionen durch Vergleichen benachbarter Elemente. Auswahlsortierung: Finden Sie das kleinste Element und tauschen Sie es an die aktuelle Position aus. Einfügungssortierung: Elemente einzeln an der richtigen Position einfügen. Schnelle Sortierung: Divide-and-Conquer-Methode, wählen Sie das Pivot-Element aus, um das Array zu teilen. Zusammenführungssortierung: Teilen und Erobern, rekursives Sortieren und Zusammenführen von Unterarrays.
 Swoole Advanced: So verwenden Sie Multithreading, um einen Hochgeschwindigkeits-Sortieralgorithmus zu implementieren
Jun 14, 2023 pm 09:16 PM
Swoole Advanced: So verwenden Sie Multithreading, um einen Hochgeschwindigkeits-Sortieralgorithmus zu implementieren
Jun 14, 2023 pm 09:16 PM
Swoole ist ein leistungsstarkes Netzwerkkommunikations-Framework, das auf der PHP-Sprache basiert. Es unterstützt die Implementierung mehrerer asynchroner E/A-Modi und mehrerer erweiterter Netzwerkprotokolle. Basierend auf Swoole können wir seine Multithreading-Funktion nutzen, um effiziente Algorithmusoperationen zu implementieren, beispielsweise Hochgeschwindigkeits-Sortieralgorithmen. Der Hochgeschwindigkeits-Sortieralgorithmus (QuickSort) ist ein gängiger Sortieralgorithmus. Durch die Lokalisierung eines Benchmark-Elements werden die Elemente, die kleiner als das Benchmark-Element sind, auf der linken Seite platziert, und diejenigen, die größer oder gleich dem Benchmark sind Element werden auf der rechten Seite platziert. Dann werden die linke und die rechte Teilsequenzrekursion platziert
 So implementieren Sie eine einfache Sortieralgorithmusfunktion mit MySQL und Java
Sep 20, 2023 am 09:45 AM
So implementieren Sie eine einfache Sortieralgorithmusfunktion mit MySQL und Java
Sep 20, 2023 am 09:45 AM
So implementieren Sie mit MySQL und Java eine einfache Sortieralgorithmusfunktion. Einführung: In der Softwareentwicklung gehören Sortieralgorithmen zu den grundlegendsten und am häufigsten verwendeten Funktionen. In diesem Artikel wird erläutert, wie Sie mithilfe von MySQL und Java eine einfache Sortieralgorithmusfunktion implementieren, und es werden spezifische Codebeispiele bereitgestellt. 1. Übersicht über Sortieralgorithmen Sortieralgorithmen sind Algorithmen, die einen Datensatz nach bestimmten Regeln anordnen. Zu den häufig verwendeten Sortieralgorithmen gehören Blasensortierung, Einfügungssortierung, Auswahlsortierung, Schnellsortierung usw. In diesem Artikel wird die Blasensortierung als Beispiel zur Erläuterung und Implementierung verwendet. 2. M
 So implementieren Sie den Auswahlsortierungsalgorithmus in C#
Sep 20, 2023 pm 01:33 PM
So implementieren Sie den Auswahlsortierungsalgorithmus in C#
Sep 20, 2023 pm 01:33 PM
So implementieren Sie den Auswahlsortierungsalgorithmus in C#. Die Auswahlsortierung (SelectionSort) ist ein einfacher und intuitiver Sortieralgorithmus. Seine Grundidee besteht darin, jedes Mal das kleinste (oder größte) Element aus den zu sortierenden Elementen auszuwählen und am Ende einzufügen die sortierte Reihenfolge. Wiederholen Sie diesen Vorgang, bis alle Elemente sortiert sind. Erfahren Sie mehr darüber, wie Sie den Auswahlsortierungsalgorithmus in C# implementieren, zusammen mit spezifischen Codebeispielen. Erstellen einer Auswahlsortierungsmethode Zuerst müssen wir eine Methode zur Implementierung der Auswahlsortierung erstellen. Diese Methode akzeptiert a
 Die zehn wichtigsten Sortieralgorithmen, die Programmierer beherrschen müssen (Teil 1)
Aug 15, 2023 pm 02:55 PM
Die zehn wichtigsten Sortieralgorithmen, die Programmierer beherrschen müssen (Teil 1)
Aug 15, 2023 pm 02:55 PM
Man kann sagen, dass Sortieralgorithmen etwas sind, das jeder Programmierer beherrschen muss. Um Ihnen das Lernen zu erleichtern, finden Sie im Folgenden eine Einführung in die Python-Implementierung.





