Beweisen Sie, dass die dominante Menge eines Graphen NP-vollständig ist

Eine dominante Menge eines Graphen ist ein NP-vollständiges Problem, bei dem es sich um eine Teilmenge von Scheitelpunkten handelt, sodass jeder Scheitelpunkt oder benachbarte Scheitelpunkt in der Teilmenge in der Teilmenge enthalten ist. Die vollständige Form von NP ist „nicht deterministisches Polynom“, das das Problem in polynomieller Zeit prüft, was bedeutet, dass wir in polynomieller Zeit prüfen können, ob die Lösung korrekt ist. Polynomiale Zeit hat die beste Komplexität für Codes wie lineare Suchzeitkomplexität – n, binäre Suche – logn, Zusammenführungssortierung – n(log)n usw. NP-vollständige Diagramme bieten eine gute Lösung in angemessener Zeit. Diese Anwendung wird in Bereichen wie Netzwerksteuerung, Topologieerstellung in Computerlabors, sozialen Netzwerken und verteiltem Rechnen eingesetzt.

Lassen Sie uns verstehen und prüfen, ob ein Knoten die dominante Menge eines vollständigen NP-Graphen hat.

Ein Scheitelpunkt soll sich selbst und jeden seiner Nachbarn dominieren.

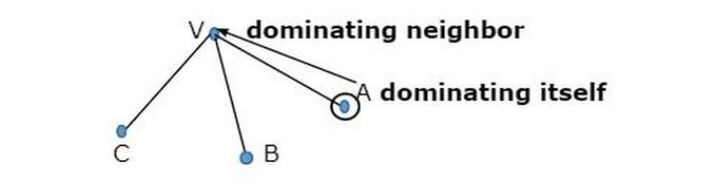
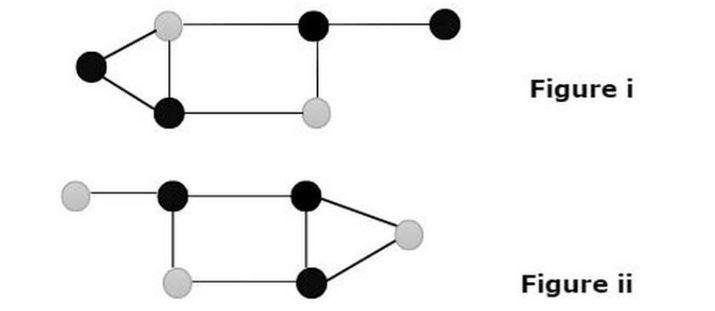
Wir sehen zwei Diagramme, die die Knoten im Diagramm zeigen, an denen in der Natur die graue Farbe dominiert.

G = V, E

Parameter

G wird als Graph betrachtet, V wird als Scheitelpunkt betrachtet und E wird als Kante betrachtet.

Bestimmen Sie anhand eines Graphen G(V, E) und einer ganzen Zahl k, ob der Graph eine dominierende Menge der Größe k hat. Eine als Problem angegebene Eingabe wird als Instanz des Problems betrachtet. Der Graph G(V, E) und die ganze Zahl k dienen als Beispiele für das Problem der dominierenden Menge, bei dem gefragt wird, ob der Graph G eine dominierende Menge in G haben kann. Da die Definition eines NP-vollständigen Problems ein Problem ist, das sowohl NP als auch NP-schwer ist, besteht der Beweis, dass ein Problem NP-vollständig ist, aus zwei Komponenten −

Dominator setzt NP-vollständige Probleme ein

Wenn es ein NP-Problem Y gibt, das sich in polynomieller Zeit auf X reduziert, dann ist X ein NP-vollständiges Problem. NP-vollständige Probleme sind genauso schwierig wie NP-Probleme. Ein Problem ist NP-vollständig, wenn es sowohl Teil eines NP-Problems als auch eines NP-schweren Problems ist. Nichtdeterministische Turingmaschinen können NP-vollständige Probleme in polynomieller Zeit lösen. Wenn ein Problem np-vollständig ist, hat es sowohl np- als auch np-harte Kombinationen.

Das bedeutet, dass Probleme mit NP-Lösungen in polynomieller Zeit verifiziert werden können.

Echte Beispiele für NP-Vollständigkeit haben dominierende Mengen wie -

• Entscheidungsproblem.

• Die Grafiken sind konsistent.

Nichtdeterministischer Suchalgorithmus

NP_search( key ) {
   arraylist[100];
   i = array_check(key);
   if(list[i]==key) {
      searching found at index i.
   } else {
      searching found at index i.
   }
}

Die Gesamtzeitkomplexität dieses Algorithmus beträgt also O(1), aber wir wissen nicht, welche Suchtechnik zur Lösung dieses Problems nützlicher ist; dies wird als nichtdeterministischer Algorithmus bezeichnet.

Dominator-Set bei NP-schweren Problemen

Ein Problem X ist NP-schwer, wenn es ein NP-vollständiges Problem Y gibt, das sich in polynomieller Zeit auf Problem X reduziert. NP-schwere Probleme sind genauso schwer wie NP-vollständige Probleme. Ein NP-schweres Problem gehört nicht unbedingt zur NP-Kategorie.

Wenn jedes NP-Problem in polynomieller Zeit gelöst werden kann, nennt man es NP-schwer. Oftmals wird ein spezifisches Problem genutzt, um andere Probleme zu lösen und zu reduzieren.

Echte Beispiele für

NP-hard haben dominierende Mengen wie -

• Hamiltonscher Zyklus

• Optimierungsprobleme

• Kürzeste Route

Fazit

Wir haben das Konzept gelernt, dass die dominante Menge eines Graphen NP-vollständig ist. Wir sehen, wie wichtig die diskrete Mathematik ist, um diese Probleme wie Hamilton-Zyklen, kürzeste Wege usw. miteinander zu verbinden. In der Programmiersprache handelt es sich bei NP-vollständigen Problemen um eine Klasse von Problemen, die schwer zu finden sind, deren Lösungen jedoch direkt in polynomieller Zeit verifiziert werden können.

Das obige ist der detaillierte Inhalt vonBeweisen Sie, dass die dominante Menge eines Graphen NP-vollständig ist. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!