Verwendung des Kruskal-Algorithmus in C++

So verwenden Sie den Kruskal-Algorithmus in C++
Der Kruskal-Algorithmus ist ein häufig verwendeter Greedy-Algorithmus zur Lösung des Minimum-Spanning-Tree-Problems. Beim Programmieren in C++ können wir den Kruskal-Algorithmus anhand einfacher Codebeispiele verstehen und verwenden.
Die Grundidee des Kruskal-Algorithmus besteht darin, kontinuierlich Kanten mit den kleinsten Kantengewichten auszuwählen, die keine Schleife bilden, bis alle Scheitelpunkte im Spanning Tree enthalten sind. Im Folgenden erklären wir Ihnen Schritt für Schritt, wie Sie mit C++ den Kruskal-Algorithmus implementieren.
Schritt 1: Datenvorbereitung
Zuerst müssen wir eine Diagrammdatenstruktur vorbereiten, um das Problem darzustellen. In C++ können Diagramme mithilfe von Adjazenzmatrizen oder Adjazenzlisten dargestellt werden. Hier verwenden wir Adjazenzlisten zur Darstellung ungerichteter Graphen.
Adjazenzlisten können mithilfe einer Kombination aus Vektoren und verknüpften Listen implementiert werden. Wir definieren zwei Strukturen, um die Eckpunkte und Kanten des Diagramms darzustellen.
// 图的顶点结构体
struct Vertex {
int id; // 顶点的唯一标识符
// ...
};
// 图的边结构体
struct Edge {
int start; // 边的起始顶点
int end; // 边的结束顶点
int weight; // 边的权重
// ...
};
// 定义一个无向图的类
class Graph {
public:
// 添加顶点和边的函数
void addVertex(Vertex v);
void addEdge(Edge e);
// ...
private:
// 保存顶点和边的数据结构
vector<Vertex> vertices;
list<Edge> edges;
// ...
};Schritt 2: Implementieren Sie den Kruskal-Algorithmus
Nachdem wir die Datenstruktur des Diagramms vorbereitet haben, können wir mit der Implementierung des Kruskal-Algorithmus beginnen. Zuerst müssen wir die Kanten des Diagramms nach Gewicht von klein nach groß sortieren. Dann verwenden wir Union-Find, um zu bestimmen, ob die ausgewählten Kanten einen Zyklus bilden. Schließlich fügen wir die ausgewählten Kanten zum minimalen Spannbaum hinzu.
Das Folgende ist der spezifische Implementierungscode des Kruskal-Algorithmus:
// 定义并查集结构体
struct UnionFind {
vector<int> parent;
// ...
};
// 初始化并查集
void initUnionFind(UnionFind& uf, int n) {
uf.parent.resize(n);
// ...
}
// 查找根节点
int findRoot(UnionFind& uf, int x) {
if (uf.parent[x] != x) {
uf.parent[x] = findRoot(uf, uf.parent[x]);
}
return uf.parent[x];
}
// 合并两个集合
void mergeSets(UnionFind& uf, int x, int y) {
int rootX = findRoot(uf, x);
int rootY = findRoot(uf, y);
if (rootX != rootY) {
uf.parent[rootX] = rootY;
}
}
// Kruskal算法主函数
list<Edge> kruskal(Graph& graph) {
list<Edge> minSpanningTree;
// 将图的边按照权重从小到大排序
graph.edges.sort([](const Edge& e1, const Edge& e2) {
return e1.weight < e2.weight;
});
int numVertices = graph.vertices.size();
UnionFind uf;
initUnionFind(uf, numVertices);
for (const Edge& edge : graph.edges) {
int startRoot = findRoot(uf, edge.start);
int endRoot = findRoot(uf, edge.end);
// 如果两个顶点不在同一个集合中,则添加该边到最小生成树中
if (startRoot != endRoot) {
minSpanningTree.push_back(edge);
mergeSets(uf, startRoot, endRoot);
}
}
return minSpanningTree;
}Schritt 3: Testcode
Schreiben Sie eine Testfunktion, erstellen Sie ein Diagramm, rufen Sie den Kruskal-Algorithmus auf und geben Sie den minimalen Spannbaum aus:
void testKruskal() {
Graph graph;
// 添加顶点和边
// ...
list<Edge> minSpanningTree = kruskal(graph);
// 输出最小生成树
for (const Edge& edge : minSpanningTree) {
cout << edge.start << " -> " << edge.end << ", weight: " << edge.weight << endl;
}
}
int main() {
testKruskal();
return 0;
}Das Obige ist die Implementierung des Kruskal-Algorithmus mit C++ Ein einfaches Beispiel. Anhand dieses Beispiels können Sie den Kruskal-Algorithmus besser verstehen und verwenden, um das Problem des minimalen Spannbaums zu lösen.
Das obige ist der detaillierte Inhalt vonVerwendung des Kruskal-Algorithmus in C++. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Verwendung des Kruskal-Algorithmus in C++
Sep 19, 2023 pm 04:10 PM
Verwendung des Kruskal-Algorithmus in C++
Sep 19, 2023 pm 04:10 PM
Verwendung des Kruskal-Algorithmus in C++ Der Kruskal-Algorithmus ist ein häufig verwendeter Greedy-Algorithmus zur Lösung des Minimum-Spanning-Tree-Problems. Beim Programmieren in C++ können wir den Kruskal-Algorithmus anhand einfacher Codebeispiele verstehen und verwenden. Die Grundidee des Kruskal-Algorithmus besteht darin, kontinuierlich die Kante mit dem kleinsten Kantengewicht auszuwählen, die keine Schleife bildet, bis alle Scheitelpunkte im Spannbaum enthalten sind. Im Folgenden erklären wir Ihnen Schritt für Schritt, wie Sie mit C++ den Kruskal-Algorithmus implementieren. Schritt eins: Datenvorbereitung Zuerst I
 Hochgeschwindigkeits-Abrufalgorithmus und seine Anwendung in PHP
Jun 22, 2023 pm 05:31 PM
Hochgeschwindigkeits-Abrufalgorithmus und seine Anwendung in PHP
Jun 22, 2023 pm 05:31 PM
Als beliebte serverseitige Programmiersprache spielt PHP eine unverzichtbare Rolle bei der Entwicklung von Webanwendungen. In der tatsächlichen Entwicklung müssen wir häufig Vorgänge wie das Abrufen und Suchen großer Datenmengen durchführen. Zu diesem Zeitpunkt sind Hochgeschwindigkeits-Abrufalgorithmen zu einer sehr wichtigen Richtung geworden. In diesem Artikel werden Hochgeschwindigkeits-Abrufalgorithmen vorgestellt, die häufig in PHP und ihren Anwendungen verwendet werden. 1. Übersicht In der Datenstruktur bezieht sich der Abruf auf das Finden von Datensätzen mit bestimmten Bedingungen in der Datensammlung. Zu den gängigen Abrufmethoden gehören die lineare Suche, die binäre Suche, die Hash-Suche usw. lineare Suche
 Warum schlägt der Minimum-Spanning-Tree-Algorithmus von Prim und Kruskal in gerichteten Graphen fehl?
Sep 02, 2023 pm 05:29 PM
Warum schlägt der Minimum-Spanning-Tree-Algorithmus von Prim und Kruskal in gerichteten Graphen fehl?
Sep 02, 2023 pm 05:29 PM
Die Prim-Methode und der Kruskal-Algorithmus sind zwei gängige Methoden zum Auffinden von MST (Minimum Spanning Tree) in ungerichteten Graphen. Diese Techniken können jedoch keine korrekte MST für gerichtete Graphen erzeugen. Dies liegt daran, dass gerichtete Graphen nicht den Grundannahmen und Methoden der Algorithmen von Prim und Kruskal entsprechen. Der Algorithmus von Prim Zunächst gibt es den Algorithmus von Prim, der das gierige Hinzufügen von Kanten zu einem expandierenden minimalen Spannbaum beinhaltet, bis alle Eckpunkte abgedeckt sind. Scheitelpunkte innerhalb des MST werden über die Kante mit dem geringsten Gewicht mit Scheitelpunkten außerhalb des MST verbunden. Da sich alle Kanten in einem ungerichteten Graphen in jede Richtung bewegen können, ist der kürzeste Weg vom MST zu externen Eckpunkten leicht zu finden. Allerdings zeigen in einem gerichteten Graphen die Kanten immer in eine Richtung und es kann sein, dass es keine gerade Linie gibt
 Verwendung von C++ zur Implementierung der geplanten Aufgabenfunktion eingebetteter Systeme
Aug 27, 2023 pm 12:05 PM
Verwendung von C++ zur Implementierung der geplanten Aufgabenfunktion eingebetteter Systeme
Aug 27, 2023 pm 12:05 PM
Verwendung von C++ zum Implementieren der geplanten Aufgabenfunktion eingebetteter Systeme Eingebettete Systeme müssen häufig die geplante Aufgabenfunktion implementieren, dh einige Aufgaben innerhalb eines bestimmten Zeitintervalls ausführen. Als leistungsstarke Programmiersprache stellt uns C++ viele Tools und Bibliotheken zur Verfügung, um solche Funktionen zu erreichen. In diesem Artikel wird die Verwendung der Programmiersprache C++ zum Implementieren geplanter Aufgabenfunktionen in eingebetteten Systemen vorgestellt und einige Codebeispiele bereitgestellt. Verwendung von Timer-Interrupts In eingebetteten Systemen können wir Timer-Interrupts verwenden, um geplante Aufgabenfunktionen zu implementieren. Durch Einstellen des Timers
 Wie implementiert man autonomes Fahren und intelligente Transportsysteme in C++?
Aug 26, 2023 am 08:58 AM
Wie implementiert man autonomes Fahren und intelligente Transportsysteme in C++?
Aug 26, 2023 am 08:58 AM
Wie implementiert man autonomes Fahren und intelligente Transportsysteme in C++? Autonomes Fahren und intelligente Transportsysteme sind derzeit heiße Themen im Bereich der künstlichen Intelligenz und ihre Anwendungsbereiche umfassen viele Aspekte wie Transport, Sicherheitsschutz und Stadtplanung. In diesem Artikel wird untersucht, wie die Programmiersprache C++ zur Implementierung autonomer Fahr- und intelligenter Transportsysteme verwendet werden kann, und es werden relevante Codebeispiele bereitgestellt. Verstehen Sie die Grundprinzipien des autonomen Fahrens und intelligenter Transportsysteme. Unter autonomen Fahrsystemen versteht man Technologien, die Computer, Sensoren und andere Geräte zum autonomen Navigieren und Fahren von Fahrzeugen nutzen. es muss in Echtzeit wahrgenommen werden
 Wie man mit C++ ein eingebettetes System mit Echtzeitfähigkeiten implementiert
Aug 25, 2023 pm 03:18 PM
Wie man mit C++ ein eingebettetes System mit Echtzeitfähigkeiten implementiert
Aug 25, 2023 pm 03:18 PM
So implementieren Sie mit C++ ein eingebettetes System mit Echtzeitfunktionen. Einführung: Mit der kontinuierlichen Weiterentwicklung der Technologie werden eingebettete Systeme in verschiedenen Bereichen häufig eingesetzt. Echtzeitfunktionalität ist ein entscheidendes Merkmal eingebetteter Systeme, insbesondere in Szenarien, die eine sofortige Reaktion auf externe Ereignisse erfordern. In diesem Artikel wird die Verwendung der C++-Sprache zur Implementierung eines eingebetteten Systems mit Echtzeitfunktionen vorgestellt und Codebeispiele gegeben. Echtzeitbetriebssystem (RTOS) Das Echtzeitbetriebssystem (RTOS) ist der Schlüssel zur Erzielung von Echtzeitfunktionalität. RTOS verfügt über Aufgabenplanung,
 Kruskals Minimum Spanning Tree-Algorithmus – Greedy-Algorithmus in C++
Aug 28, 2023 pm 03:05 PM
Kruskals Minimum Spanning Tree-Algorithmus – Greedy-Algorithmus in C++
Aug 28, 2023 pm 03:05 PM
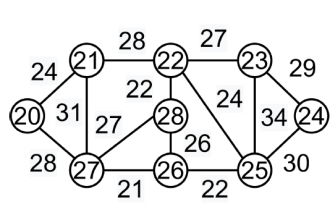
Ein Spanning Tree ist ein Teilgraph eines gerichteten ungerichteten Graphen, der alle Knoten verbindet. In einem Diagramm können sich viele Spannbäume befinden. Der minimale Spannbaum (MST) in jedem Diagramm hat das gleiche oder ein geringeres Gewicht als alle anderen Spannbäume. Den Kanten des Spannbaums werden Gewichte zugewiesen, und die Summe ist das Gewicht, das jeder Kante zugewiesen wird. Da V die Anzahl der Eckpunkte im Diagramm ist, beträgt die Anzahl der Kanten des minimalen Spannbaums (V-1), wobei V die Anzahl der Kanten ist. Verwenden Sie den Kruskal-Algorithmus, um den minimalen Spannbaum zu finden. Alle Kanten sollten in nicht absteigender Reihenfolge nach Gewicht angeordnet werden. Wählen Sie die kleinste Seite. Wird keine Schlaufe gebildet, wird die Kante mit einbezogen. Schritt 2 sollte durchgeführt werden, bis der Spannbaum (V-1) Kanten hat. In diesem Fall wird uns gesagt, dass wir den Greedy-Ansatz verwenden sollen. Die gierige Option besteht darin, die Kante mit dem geringsten Gewicht zu wählen. Beispiel: Der minimale Spannbaum dieses Diagramms ist (9-1)=8
 So implementieren Sie den Kruskal-Algorithmus in Java
May 11, 2023 pm 10:19 PM
So implementieren Sie den Kruskal-Algorithmus in Java
May 11, 2023 pm 10:19 PM
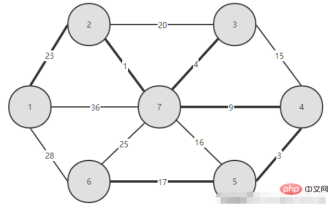
Wir stellen einen weiteren Algorithmus zur Konstruktion eines minimalen Spannbaums vor, den Kruskal-Algorithmus: Sei der Graph G = (V, E) ein ungerichteter verbundener gewichteter Graph, V = {1, 2,...n}; sei der minimale Spannbaum T = (V, TE), der Anfangszustand des Baumes ist ein nicht verbundener Graph mit nur n Knoten und keinen Kanten T = (V, {}). Kruskals Algorithmus behandelt diese n Knoten als n isolierte verbundene Zweige. Zuerst werden alle Kanten entsprechend ihrer Gewichtung von klein nach groß sortiert. Wenn dann die Anzahl der in T auszuwählenden Kanten kleiner als n-1 ist, wird eine gierige Auswahl wie folgt durchgeführt: Wählen Sie die Kante (i, j) aus. mit dem kleinsten Gewicht in der Kantenmenge E), wenn das Hinzufügen von Kante (i, j) zur Menge TE keinen Zyklus erzeugt, dann füge Kante (i, j) zur Kantenmenge TE hinzu, das heißt, verwende Kante (i , j) um die beiden Zweige zu einem zusammenzuführen






