Finden Sie mit dem Floyd-Warshal-Algorithmus den kürzesten Weg zwischen zwei beliebigen Knoten

C++ verfügt über ein Makro, das als Codeabschnitt oder erwarteter Wert definiert ist und immer dann wiederverwendet wird, wenn der Benutzer es benötigt. Der Floyd-Walshall-Algorithmus ist der Prozess, den kürzesten Weg zwischen allen Scheitelpunktpaaren in einem gegebenen gewichteten Graphen zu finden. Der Algorithmus folgt einem dynamischen Programmieransatz, um den Minimalgewichtsgraphen zu finden.

Lassen Sie uns die Bedeutung des Freud-Walshire-Algorithmus anhand von Diagrammen verstehen -

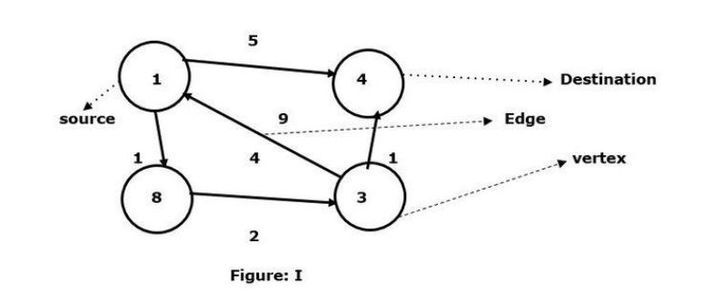
Mit Scheitelpunkt 1 als Quelle und Scheitelpunkt 4 als Ziel finden Sie den kürzesten Weg zwischen ihnen.

Wir haben gesehen, dass es zwei Pfade gibt, die mit dem Zielscheitelpunkt 4 verbunden werden können.

• 1 -> 4 – Die Kante hat ein Gewicht von 5

• 1 -> 8 -> 4 – Das Kantengewicht (1+2+1) beträgt 4.

In der gegebenen Grafik I sehen wir die minimale Kante, die zwei Eckpunkte verbindet. Hier also der Pfad vom Scheitelpunkt 8 zum Scheitelpunkt 3, der Scheitelpunkt 1 mit Scheitelpunkt 4 verbindet und die Kante ist 4. Andererseits gibt es eine gerichtete Kante vom Scheitelpunkt 1 zum Scheitelpunkt 4, und das Gewicht der Kante beträgt 5.

Jetzt vergleichen wir zwei Gewichte, nämlich 4 und 5. Daher ist hier 4 das Mindestgewicht des Diagramms, berechnet nach dem Floyd Warshall-Algorithmus.

In diesem Artikel verwenden wir den Floyd Warshall-Algorithmus, um den kürzesten Weg zwischen zwei beliebigen Knoten zu finden.

Grammatik

Die folgende Syntax wird im Programm verwendet -

data_type[][] array_name;

Parameter

data_type[][] – Der vom Benutzer erwähnte Datentyp. Das erste Array repräsentiert Zeilen und das zweite Array repräsentiert Spalten. Dies stellt also ein zweidimensionales Array dar.

array_name – Der dem Array gegebene Name.

Algorithmus

• Wir starten das Programm mit der Header-Datei 'iostream' und definieren den Makrospeicherort als 'INF' (unendlich), da es später die 2D-Array-Matrix und die if-else-Anweisung erfüllt.

• Als nächstes erstellen wir eine globale Funktionsdefinition namens 'printPath' und akzeptieren drei Parameter, 'parent[]', 'i' und 'j', um zu überprüfen, ob der Pfad existiert.

• Dann starten wir die Hauptfunktion und speichern den Wert ‘4’ in der Variablen ‘V’, die die Anzahl der Eckpunkte darstellt. Zweitens speichern Sie den Wert in Form einer Adjazenzmatrix in der Variablen ‘dist[V][V]‘. Wie wir wissen, stellt dist[i][j] eine 2D-Matrix dar, die das Gewicht der Kante von ‘i‘ bis ‘j‘ definiert, indem die Adjazenzmatrix gespeichert wird.

• Als nächstes initialisieren wir ein 2D-Array für die Variable ‘parent’ mit der Größe [V][V].

In dieser Variablen verwenden wir, um jedes Scheitelpunktpaar 'i' und 'j' in Bezug auf 'parent[i][j]'< /b>.

anzuzeigen

• Durch die Verwendung zweier verschachtelter for-Schleifen finden wir den kürzesten Weg. Die erste for-Schleife durchläuft die Zeilen in der Matrix. Dann durchlaufen wir die Spalten in der Matrix durch die zweite for-Schleife und dann überprüfen wir die folgende Bedingung mit der if-else-Anweisung -

• If (dist[i][j] != INF && i != j) { Die chinesische Übersetzung von parent[i][j] = i;}

  lautet: parent[i][j] = i;}

  In der if-Anweisung verwenden wir den 'and' (&&)-Operator, um zwei Bedingungen auszudrücken. Wenn beide Bedingungen erfüllt sind, wird 'i' in 'parent[i][j]' gespeichert, wodurch dies überprüft wird Der Pfad existiert.

• Andere{ Die chinesische Übersetzung von parent[i][j] = -1;}

  lautet: parent[i][j] = -1;}

  In der else-Anweisung initialisieren wir „-1“ mit „parent[i][j]“, um zu überprüfen, dass der Pfad nicht existiert.

• Jetzt beginnen wir mit drei verschachtelten for-Schleifen und wenden k Eckpunkte im Bereich von 0 bis V-1 an. Mit Hilfe dieses Bereichs werden unsere kürzeste Distanz und unser kürzester Pfad aktualisiert. In der dritten verschachtelten Schleife verwenden wir die folgende Bedingung wie

if (dist[i][j] < dist[i][k] + dist[k][j]){
   dist[i][j] = dist[i][k] + dist[k][j]; 
   parent[i][j] = parent[k][j];	
}

Hier aktualisiert K die Zeilen- und Spaltenteile der 2D-Array-Matrix, wodurch der neu aktualisierte kürzeste Pfad und die kürzeste Entfernung überprüft werden.

• Als nächstes drucken wir die kürzeste Distanz und den kürzesten Weg aller Scheitelpunktpaare aus, indem wir die folgenden Bedingungen angeben

• Durch die Verwendung von zwei verschachtelten for-Schleifen drucken wir die kürzeste Entfernung und den kürzesten Pfad.

• Durch die Verwendung der if-Anweisung unter der zweiten for-Schleife prüfen wir, ob dist[i][j] gleich unendlich ist. Wenn sich herausstellt, dass es unendlich ist, geben Sie „INF“ aus, andernfalls geben Sie den kürzesten Pfad aus.

• Schließlich rufen wir die Funktion 'printPath()' auf, indem wir drei Parameter (parent[i], i und j) übergeben.

Beispiel

In diesem Programm verwenden wir den Floyd Warshall-Algorithmus, um den kürzesten Weg zwischen zwei beliebigen Knoten zu berechnen.

#include <iostream> 
using namespace std; 
#define INF 1000000000 // Infinity

void printPath(int parent[], int i, int j) {
   if (i == j) 
      cout << i << " "; 
   else if (parent[j] == -1) 
     cout << "No path exists"; 
   else
   { 
      printPath(parent, i, parent[j]); 
      cout << j << " "; 
   }
} 

int main() 
{
   int V = 4; 
   // V represent number of vertices
   int dist[V][V] = {{0, 2, INF, 4}, 
      {6, 0, 5, 3}, 
      {INF, 10, 0, 1}, 
      {7, 9, 8, 0}}; 
   // Represent the graph using adjacency matrix

   // Apply the Floyd Warshall algorithm to find the shortest paths
   int parent[V][V];
   for (int i = 0; i < V; i++) 
   { 
      for (int j = 0; j < V; j++) 
      {
         if (dist[i][j] != INF && i != j)
         parent[i][j] = i;
         else
         parent[i][j] = -1;
      }
   }
   // update the path and distance using the k vertex range from 0 to V-1.
   for (int k = 0; k < V; k++) 
   { 
      for (int i = 0; i < V; i++) 
      { 
         for (int j = 0; j < V; j++) 
         { 
            if (dist[i][j] > dist[i][k] + dist[k][j]) 
            {
               dist[i][j] = dist[i][k] + dist[k][j];
               parent[i][j] = parent[k][j];	
            }
         }
      }
   }

   // Print shortest distances and paths between all pairs of vertices
   for (int i = 0; i < V; i++) 
   { 
      for (int j = 0; j < V; j++) 
      { 
         cout << "The Shortest distance between " << i << " and " << j << " is ";
         if (dist[i][j] == INF) 
            cout << "INF "; 
         else
            cout << dist[i][j] << " ";

         cout << "and the shortest path is:- ";
         printPath(parent[i], i, j);
         cout << endl;
      } 
   } 

   return 0; 
}

输出

The Shortest distance between 0 and 0 is 0 and the shortest path is:- 0 
The Shortest distance between 0 and 1 is 2 and the shortest path is:- 0 1 
The Shortest distance between 0 and 2 is 7 and the shortest path is:- 0 1 2 
The Shortest distance between 0 and 3 is 4 and the shortest path is:- 0 3 
The Shortest distance between 1 and 0 is 6 and the shortest path is:- 1 0 
The Shortest distance between 1 and 1 is 0 and the shortest path is:- 1 
The Shortest distance between 1 and 2 is 5 and the shortest path is:- 1 2 
The Shortest distance between 1 and 3 is 3 and the shortest path is:- 1 3 
The Shortest distance between 2 and 0 is 8 and the shortest path is:- 2 3 0 
The Shortest distance between 2 and 1 is 10 and the shortest path is:- 2 1 
The Shortest distance between 2 and 2 is 0 and the shortest path is:- 2 
The Shortest distance between 2 and 3 is 1 and the shortest path is:- 2 3 
The Shortest distance between 3 and 0 is 7 and the shortest path is:- 3 0 
The Shortest distance between 3 and 1 is 9 and the shortest path is:- 3 1 
The Shortest distance between 3 and 2 is 8 and the shortest path is:- 3 2 
The Shortest distance between 3 and 3 is 0 and the shortest path is:- 3 

结论

我们学习了使用Floyd Warshall算法找到任意两个节点之间的最短路径的概念。我们使用邻接矩阵作为程序的输入，通过它我们找到了最短路径和距离。此外，为了更新路径和距离，我们使用了k个顶点来更新行和列。在我们的日常生活中，我们在谷歌地图上搜索最短路线或路径，从一个起点到目的地。

Das obige ist der detaillierte Inhalt vonFinden Sie mit dem Floyd-Warshal-Algorithmus den kürzesten Weg zwischen zwei beliebigen Knoten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!