 Backend-Entwicklung
Backend-Entwicklung
 C++
C++
 Überprüft, ob eine Permutation einer bestimmten Zeichenfolge lexikographisch größer ist als eine andere angegebene Zeichenfolge
Überprüft, ob eine Permutation einer bestimmten Zeichenfolge lexikographisch größer ist als eine andere angegebene Zeichenfolge
Überprüft, ob eine Permutation einer bestimmten Zeichenfolge lexikographisch größer ist als eine andere angegebene Zeichenfolge

Wir haben zwei Zeichenfolgen erhalten und müssen prüfen, ob eine Permutation der angegebenen Zeichenfolge existiert, damit eine Permutation am i-ten Index größere Zeichen als die andere Permutation haben kann.
Wir können das Problem lösen, indem wir die Zeichenfolge sortieren und jedes Zeichen in der Zeichenfolge einzeln vergleichen. Alternativ können wir die Zeichenhäufigkeiten der beiden Zeichenfolgen verwenden, um das Problem zu lösen.
Problemstellung – Wir erhalten die Zeichenfolgen str1 und str2 der Länge N. Wir müssen prüfen, ob es Permutationen von Zeichenfolgen gibt, sodass eine lexikographisch größer ist als die andere. Dies bedeutet, dass jede Permutation ein Zeichen am i-ten Index haben sollte, das größer ist als das Zeichen am i-ten Index einer anderen Zeichenfolgenpermutation.
Beispiel
Eingabe - str1 = "aef"; str2 = "fgh";
Ausgabe – Ja
Erklärung – „fgh“ ist bereits größer als „aef“. Hier gilt a > f, g >
Eingabe– str1 = „adsm“; str2 = „obpc“;
Ausgabe – Nein
Erklärung– Wir können keine Permutation finden, bei der jedes Zeichen einer Zeichenfolge größer als das andere ist.
Methode 1
Bei dieser Methode sortieren wir zwei Zeichenfolgen in lexikografischer Reihenfolge. Anschließend vergleichen wir jedes Zeichen der Zeichenfolge. Gibt „true“ zurück, wenn alle Zeichen von str1 kleiner als str2 sind oder wenn alle Zeichen von str2 kleiner als str1 sind. Andernfalls wird false zurückgegeben.
Algorithmus
Verwenden Sie die Methode sort(), um Zeichenfolgen zu sortieren.
Definieren Sie die boolesche Variable isStr1Greater und initialisieren Sie sie mit true.
Durchlaufen Sie die Zeichenfolge. Wenn das Zeichen an der i-ten Indexposition in str1 kleiner als str2 ist, aktualisieren Sie den Wert von isStr1Greater auf false und unterbrechen Sie die Schleife mit dem Schlüsselwort break.
Wenn isStr1Greater true ist, wird die Schleife erfolgreich abgeschlossen und gibt true zurück.
Durchlaufen Sie nun die Zeichenfolge, um zu prüfen, ob str2 größer als str1 ist. Wenn wir feststellen, dass ein Zeichen von str1 größer als str2 ist, wird false zurückgegeben.
Gibt true zurück, wenn die Schleife erfolgreich abgeschlossen wird.
Beispiel
#include <algorithm>
#include <iostream>
#include <string>
using namespace std;
bool isAnyPermLarge(string string1, string string2) {
// sort the strings
sort(string1.begin(), string1.end());
sort(string2.begin(), string2.end());
// to keep track if string1 is greater than string2
bool isStr1Greater = true;
// traverse the string
for (int i = 0; i < string1.length(); i++) {
// if any character of string1 is less than string2, return false.
if (string1[i] < string2[i]) {
isStr1Greater = false;
break;
}
}
// If string1 is greater, returning true
if (isStr1Greater)
return true;
// traverse the string
for (int i = 0; i < string2.length(); i++) {
// if any character of string2 is less than string1, return false.
if (string1[i] > string2[i]) {
return false;
}
}
// return true if string2 is greater than string1
return true;
}
int main() {
string string1 = "aef";
string string2 = "fgh";
bool res = isAnyPermLarge(string1, string2);
if (res) {
cout << "Yes, permutation exists such that one string is greater than the other.";
} else {
cout << "No, permutation does not exist such that one string is greater than the other.";
}
return 0;
}
Ausgabe
Yes, permutation exists such that one string is greater than the other.
Zeitkomplexität – O(N*logN), weil wir die Strings sortieren.
Raumkomplexität – O(N) ist zum Sortieren von Zeichenfolgen erforderlich.
Methode 2
Bei dieser Methode speichern wir die Gesamthäufigkeit jedes Zeichens in beiden Zeichenfolgen. Anschließend werden wir die kumulativen Häufigkeiten verwenden, um zu entscheiden, ob wir Permutationen von Zeichenfolgen finden können, bei denen eine größer als die andere ist.
Algorithmus
Definieren Sie die Arrays „map1“ und „map2“ mit der Länge 26 und initialisieren Sie sie auf Null.
Speichern Sie die Häufigkeit der Zeichen in str1 in Map1 und speichern Sie die Häufigkeit der Zeichen in str2 in Map2.
Definieren Sie die booleschen Variablen isStr1 und isStr2 und initialisieren Sie sie mit „false“, um zu verfolgen, ob str1 größer als str2 ist.
Definieren Sie die Variablen cnt1 und cnt2, um die kumulative Häufigkeit von Zeichenfolgenzeichen zu speichern.
Durchqueren Sie Karte1 und Karte2. Fügen Sie „map1[i]“ zu „cnt1“ und „map2[i]“ zu „cnt2“ hinzu.
Wenn cnt1 größer als cnt2 ist, ist die kumulative Häufigkeit der Zeichen von str1 bis zum i-ten Index größer. Wenn ja und str2 bereits größer ist, wird „false“ zurückgegeben. Andernfalls ändern Sie isStr1 in true
Wenn cnt2 größer als cnt1 ist, ist die kumulative Häufigkeit des Zeichens am i-ten Index in str2 größer. Wenn ja und str1 bereits größer ist, wird „false“ zurückgegeben. Andernfalls ändern Sie isStr2 in true
Endlich gibt true zurück.
Beispiel
#include <iostream>
#include <string>
using namespace std;
bool isAnyPermLarge(string string1, string string2) {
int map1[26] = {0};
int map2[26] = {0};
// store the frequency of each character in the map1
for (int i = 0; i < string1.length(); i++) {
map1[string1[i] - 'a']++;
}
// store the frequency of each character in the map2
for (int i = 0; i < string2.length(); i++) {
map2[string2[i] - 'a']++;
}
// To keep track of which string is smaller. Initially, both strings are equal.
bool isStr1 = false, isStr2 = false;
// to count the cumulative frequency of characters of both strings
int cnt1 = 0, cnt2 = 0;
// traverse for all characters.
for (int i = 0; i < 26; i++) {
// update the cumulative frequency of characters
cnt1 += map1[i];
cnt2 += map2[i];
if (cnt1 > cnt2) {
// If string2 is already greater and cumulative frequency of string1 is greater than string2, then return false
if (isStr2)
return false;
// update isStr1 to true as string1 is smaller
isStr1 = true;
}
if (cnt1 < cnt2) {
// If string1 is already greater and cumulative frequency of string2 is greater than string1, then return false
if (isStr1)
return false;
// update isStr2 to true as string2 is smaller
isStr2 = true;
}
}
return true;
}
int main() {
string string1 = "aef";
string string2 = "fgh";
bool res = isAnyPermLarge(string1, string2);
if (res) {
cout << "Yes, permutation exists such that one string is greater than the other.";
} else {
cout << "No, permutation does not exist such that one string is greater than the other.";
}
return 0;
}
Ausgabe
Yes, permutation exists such that one string is greater than the other.
Zeitkomplexität – O(N), da wir die Häufigkeit von Zeichen zählen.
Raumkomplexität – O(26), weil wir die Häufigkeit der Zeichen im Array speichern.
Wir haben gelernt, zu prüfen, ob es eine Permutation zweier Zeichenfolgen gibt, sodass alle Zeichen einer Zeichenfolge größer sein können als die der anderen Zeichenfolge. Die erste Methode verwendet eine Sortiermethode und die zweite Methode verwendet die kumulative Häufigkeit von Zeichen.
Das obige ist der detaillierte Inhalt vonÜberprüft, ob eine Permutation einer bestimmten Zeichenfolge lexikographisch größer ist als eine andere angegebene Zeichenfolge. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Wie aktiviere ich die NFC-Funktion auf dem Xiaomi Mi 14 Pro?
Mar 19, 2024 pm 02:28 PM
Wie aktiviere ich die NFC-Funktion auf dem Xiaomi Mi 14 Pro?
Mar 19, 2024 pm 02:28 PM
Heutzutage werden Leistung und Funktionen von Mobiltelefonen immer leistungsfähiger. Nahezu alle Mobiltelefone sind mit komfortablen NFC-Funktionen ausgestattet, um Benutzern das mobile Bezahlen und die Identitätsauthentifizierung zu erleichtern. Einige Xiaomi 14Pro-Benutzer wissen jedoch möglicherweise nicht, wie sie die NFC-Funktion aktivieren können. Als nächstes möchte ich es Ihnen im Detail vorstellen. Wie aktiviere ich die NFC-Funktion auf dem Xiaomi 14Pro? Schritt 1: Öffnen Sie das Einstellungsmenü Ihres Telefons. Schritt 2: Suchen Sie die Option „Verbinden und teilen“ oder „Drahtlos und Netzwerke“ und klicken Sie darauf. Schritt 3: Suchen Sie im Menü „Verbindung & Freigabe“ oder „Drahtlos & Netzwerke“ nach „NFC & Zahlungen“ und klicken Sie darauf. Schritt 4: Suchen Sie nach „NFC Switch“ und klicken Sie darauf. Im Allgemeinen ist die Standardeinstellung deaktiviert. Schritt 5: Klicken Sie auf der NFC-Umschaltseite auf die Schaltfläche zum Einschalten.
 So legen Sie den Zeilenabstand in WPS Word fest, um das Dokument übersichtlicher zu gestalten
Mar 20, 2024 pm 04:30 PM
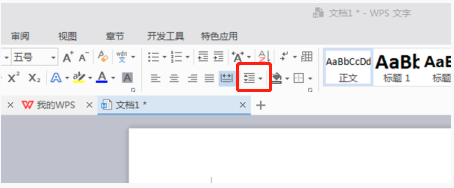
So legen Sie den Zeilenabstand in WPS Word fest, um das Dokument übersichtlicher zu gestalten
Mar 20, 2024 pm 04:30 PM
WPS ist unsere häufig verwendete Office-Software. Bei der Bearbeitung langer Artikel sind die Schriftarten oft zu klein, um klar gesehen zu werden, daher werden die Schriftarten und das gesamte Dokument angepasst. Zum Beispiel: Durch Anpassen des Zeilenabstands wird das gesamte Dokument sehr klar. Ich schlage vor, dass alle Freunde diesen Arbeitsschritt lernen. Die spezifischen Arbeitsschritte sind wie folgt. Öffnen Sie die WPS-Textdatei, die Sie anpassen möchten, suchen Sie die Symbolleiste für die Absatzeinstellung im Menü [Start] und Sie sehen das kleine Symbol für die Einstellung des Zeilenabstands (im Bild als roter Kreis dargestellt). 2. Klicken Sie auf das kleine umgekehrte Dreieck in der unteren rechten Ecke der Zeilenabstandseinstellung. Der entsprechende Zeilenabstandswert wird angezeigt. Sie können den 1- bis 3-fachen Zeilenabstand auswählen (wie durch den Pfeil in der Abbildung dargestellt). 3. Oder klicken Sie mit der rechten Maustaste auf den Absatz und er wird angezeigt
 Mar 18, 2024 pm 03:00 PM
Mar 18, 2024 pm 03:00 PM
Das Gleiten des Bildschirms durch die Luft ist eine Funktion von Huawei, die in der Huawei mate60-Serie sehr gelobt wird. Diese Funktion nutzt den Lasersensor am Telefon und die 3D-Tiefenkamera der Frontkamera, um eine Reihe von Funktionen auszuführen, die nicht erforderlich sind Funktion zum Berühren des Bildschirms, z. B. das Wischen von TikTok aus der Luft, aber wie kann man mit dem Huawei Pocket 2 TikTok aus der Luft wischen? Wie mache ich mit Huawei Pocket2 Screenshots aus der Luft? 1. Öffnen Sie die Einstellungen des Huawei Pocket2 2. Wählen Sie dann [Barrierefreiheit]. 3. Klicken Sie, um [Smart Perception] zu öffnen. 4. Schalten Sie einfach die Schalter [Air Swipe Screen], [Air Screenshot] und [Air Press] ein. 5. Wenn Sie es verwenden, müssen Sie es 20–40 cm vom Bildschirm entfernt halten, Ihre Handfläche öffnen und warten, bis das Handflächensymbol auf dem Bildschirm erscheint.
 CAD-Zeichnungen des iPhone 16 Pro werden angezeigt und eine zweite neue Schaltfläche hinzugefügt
Mar 09, 2024 pm 09:07 PM
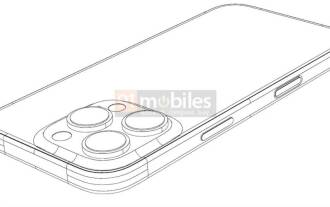
CAD-Zeichnungen des iPhone 16 Pro werden angezeigt und eine zweite neue Schaltfläche hinzugefügt
Mar 09, 2024 pm 09:07 PM
Die CAD-Dateien des iPhone 16 Pro wurden veröffentlicht und das Design stimmt mit früheren Gerüchten überein. Letzten Herbst hat das iPhone 15 Pro eine Aktionstaste hinzugefügt, und in diesem Herbst plant Apple offenbar, kleinere Anpassungen an der Größe der Hardware vorzunehmen. Hinzufügen einer Aufnahmetaste Gerüchten zufolge könnte das iPhone 16 Pro eine zweite neue Taste hinzufügen, was nach dem letzten Jahr das zweite Jahr in Folge sein wird, in dem eine neue Taste hinzugefügt wird. Gerüchten zufolge wird die neue Aufnahmetaste auf der unteren rechten Seite des iPhone 16 Pro angebracht. Dieses Design soll die Kamerasteuerung komfortabler machen und auch die Verwendung der Aktionstaste für andere Funktionen ermöglichen. Dieser Knopf wird nicht länger nur ein gewöhnlicher Auslöser sein. Bezüglich der Kamera, vom aktuellen iP
 So wechseln Sie die Sprache in Microsoft-Teams
Feb 23, 2024 pm 09:00 PM
So wechseln Sie die Sprache in Microsoft-Teams
Feb 23, 2024 pm 09:00 PM
In Microsoft Teams stehen viele Sprachen zur Auswahl. Wie kann man also die Sprache wechseln? Benutzer müssen auf das Menü klicken, dann „Allgemein“ auswählen, dann auf „Sprache“ klicken, die Sprache auswählen und sie speichern. Nachfolgend finden Sie eine detaillierte Einführung. Bar! So wechseln Sie die Sprache in Microsoft Teams Antwort: Wählen Sie den spezifischen Prozess unter „Einstellungen – Allgemein – Sprache“ aus: 1. Klicken Sie zunächst auf die drei Punkte neben dem Avatar, um die Einstellungen einzugeben. 2. Klicken Sie dann auf die allgemeinen Optionen im Inneren. 3. Klicken Sie dann auf die Sprache und scrollen Sie nach unten, um weitere Sprachen anzuzeigen. 4. Klicken Sie abschließend auf Speichern und neu starten.
 Wie stelle ich einen benutzerdefinierten Klingelton auf dem Redmi K70E ein?
Feb 24, 2024 am 10:00 AM
Wie stelle ich einen benutzerdefinierten Klingelton auf dem Redmi K70E ein?
Feb 24, 2024 am 10:00 AM
Das Redmi K70E ist zweifellos ein hervorragendes Mobiltelefon mit einem Preis von knapp über 2.000 Yuan und kann als eines der kostengünstigsten Mobiltelefone seiner Klasse bezeichnet werden. Viele Benutzer, die Wert auf Kosteneffizienz legen, haben dieses Telefon gekauft, um verschiedene Funktionen des Redmi K70E zu nutzen. Wie stellt man einen benutzerdefinierten Klingelton für das Redmi K70E ein? Wie stelle ich einen benutzerdefinierten Klingelton für das Redmi K70E ein? Um einen benutzerdefinierten Klingelton für eingehende Anrufe für das Redmi K70E festzulegen, können Sie die folgenden Schritte ausführen: Öffnen Sie die Einstellungsanwendung Ihres Telefons, suchen Sie in der Einstellungsanwendung die Option „Töne und Vibration“ oder „Ton“ und klicken Sie auf „Klingelton für eingehende Anrufe“. oder „Telefonklingelton“ Option. In den Klingeltoneinstellungen
 Der Unterschied und die vergleichende Analyse zwischen C-Sprache und PHP
Mar 20, 2024 am 08:54 AM
Der Unterschied und die vergleichende Analyse zwischen C-Sprache und PHP
Mar 20, 2024 am 08:54 AM
Unterschiede und vergleichende Analyse zwischen C-Sprache und PHP C-Sprache und PHP sind beide gängige Programmiersprachen, weisen jedoch in vielen Aspekten offensichtliche Unterschiede auf. In diesem Artikel wird eine vergleichende Analyse der C-Sprache und PHP durchgeführt und die Unterschiede zwischen ihnen anhand spezifischer Codebeispiele veranschaulicht. 1. Syntax und Verwendung: C-Sprache: Die C-Sprache ist eine prozessorientierte Programmiersprache, die hauptsächlich für die Programmierung auf Systemebene und die eingebettete Entwicklung verwendet wird. Die Syntax der C-Sprache ist relativ einfach und auf niedriger Ebene, kann den Speicher direkt bedienen und ist effizient und flexibel. Die C-Sprache betont die Vollständigkeit des Programms durch den Programmierer
 Vergleich und Analyse der Vor- und Nachteile der PHP7.2- und 5-Versionen
Feb 27, 2024 am 10:51 AM
Vergleich und Analyse der Vor- und Nachteile der PHP7.2- und 5-Versionen
Feb 27, 2024 am 10:51 AM
Vergleich und Analyse der Vor- und Nachteile von PHP7.2 und 5. PHP ist eine äußerst beliebte serverseitige Skriptsprache und wird häufig in der Webentwicklung verwendet. Allerdings wird PHP in verschiedenen Versionen ständig aktualisiert und verbessert, um den sich ändernden Anforderungen gerecht zu werden. Derzeit ist PHP7.2 die neueste Version, die im Vergleich zur vorherigen PHP5-Version viele bemerkenswerte Unterschiede und Verbesserungen aufweist. In diesem Artikel vergleichen wir die Versionen PHP7.2 und PHP5, analysieren ihre Vor- und Nachteile und stellen spezifische Codebeispiele bereit. 1. Leistungs-PH



