Siebeneckzahl
Eine Siebeneckzahl ist eine Zahl, die als Siebeneck dargestellt werden kann. Eine Siebeneckzahl kann als Kombination aufeinanderfolgender Siebeneckschichten dargestellt werden (siehe folgende Abbildungen).
 Die erste siebeneckige Zahl ist 1. Daher kann es durch einen kleinen Punkt dargestellt werden.
Die erste siebeneckige Zahl ist 1. Daher kann es durch einen kleinen Punkt dargestellt werden.
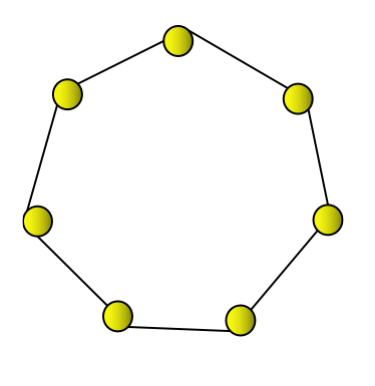 Die zweite siebeneckige Zahl ist 7, die durch ein Siebeneck dargestellt werden kann.
Die zweite siebeneckige Zahl ist 7, die durch ein Siebeneck dargestellt werden kann.
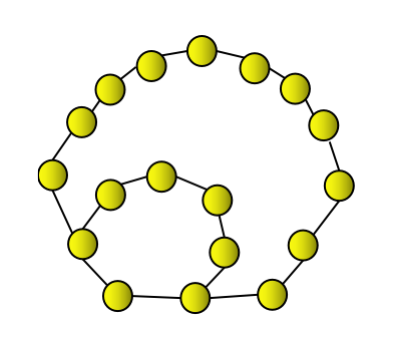 Die dritte Siebeneckzahl ist 18, die durch ein Siebeneck dargestellt und mit einer durchgehenden Siebeneckschicht kombiniert werden kann.
Die dritte Siebeneckzahl ist 18, die durch ein Siebeneck dargestellt und mit einer durchgehenden Siebeneckschicht kombiniert werden kann.
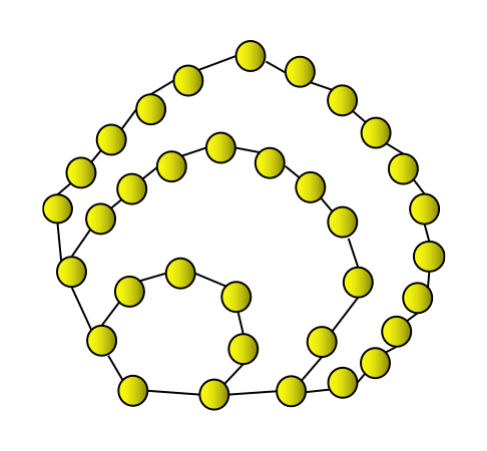 Die vierte siebeneckige Zahl ist 34. Es kann wie oben gezeigt als Siebeneck plus zwei aufeinanderfolgende Schichten von Siebenecken dargestellt werden, was 34 ergibt.
Die vierte siebeneckige Zahl ist 34. Es kann wie oben gezeigt als Siebeneck plus zwei aufeinanderfolgende Schichten von Siebenecken dargestellt werden, was 34 ergibt. Ähnliche Konzepte werden für weitere siebeneckige Zahlen verwendet. Der gleichen Logik folgend sind die ersten paar siebeneckigen Zahlen
1, 7, 18, 34, 55, 81, 112, 148, 189, 235, 286, 342, 403…
In diesem Problem besteht unsere Aufgabe darin, eine beliebige positive Zahl N als Eingabe zu geben und die N-te Siebeneckzahl als Ausgabe auszugeben.Zum Beispiel
EINGABE: N=6
Ausgabe: 81
EINGABE: N=9
Ausgabe: 189
Schauen wir uns nun den Algorithmus an, den wir zur Lösung dieses Problems verwenden werden.Algorithmus
Um dieses Problem zu lösen, müssen wir das Muster sehen, dem die Berechnung der n-ten Siebeneckzahl folgt. Die n-te siebeneckige Zahl kann als −
ausgedrückt werden
$$Heptagonal_{n}:=:frac{n}{2}(5n:-:3)$$Wenn wir uns diesen Ausdruck genau ansehen, hat jede siebeneckige Zahl die folgende Form
$frac{n}{2}(5n:-:3)$, wobei n die Anzahl der siebeneckigen Zahlen darstellt.
Lassen Sie es uns anhand eines Beispiels besser verstehen.
Für n=1 ist $frac{1}{2}(5:times:1:-:3)$= 1, was die erste siebeneckige Zahl ist.
Für n=2 ist $frac{2}{2}(5:times:2:-:3)$= 7, was die zweite siebeneckige Zahl ist.
Wenn n=3, $frac{3}{2}(5:times:3:-:3)$= 18, was die dritte siebeneckige Zahl ist.
Lassen Sie uns nun den Fall von n=8 überprüfen. Das von $frac{8}{2}(5:times:8:-:3)$ erhaltene Ergebnis ist 148, was tatsächlich die achte siebeneckige Zahl in der Folge der siebeneckigen Zahlen ist.
Da wir mit dem obigen Ausdruck jede n-te siebeneckige Zahl erhalten können, verwenden wir in unserer Methode diesen Ausdruck, um die n-te siebeneckige Zahl zu berechnen, wobei n jede positive Zahl sein kann.
Methode
Wir erklären es in den folgenden Schritten:
- Nehmen Sie eine beliebige positive Zahl N als Eingabe und berechnen Sie den entsprechenden siebeneckigen Wert N.
- Initialisieren Sie eine Funktion, um die N-te Siebeneckzahl zu berechnen.
- Verwenden Sie den im Algorithmusabschnitt erwähnten Ausdruck, d. h. $frac{N}{2}(5N:-:3)$, um die N-te Siebeneckzahl zu berechnen und sie in einer beliebigen Variablen zu speichern.
- Gibt unsere gespeicherte Variable zurück, die der Wert der N-ten siebeneckigen Zahl ist, die einem beliebigen positiven Wert N entspricht.
Hinweis − Wir verwenden den Gleitkomma-Datentyp anstelle des Ganzzahl-Datentyps, um Fehler aufgrund von Dezimalwerten bei der Berechnung der N-ten siebeneckigen Zahl mithilfe der obigen Formel zu vermeiden. Die chinesische Übersetzung von
Beispiellautet:
BeispielImplementieren Sie diese Methode in C++ −
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
//function to calculate nth heptagonal number using formula n/2(5n-3)
float heptagonal(float N){
float ans= (N/2)*((5*N) - 3); //to store nth heptagonal number
return ans;
}
int main(){
float N=5; //input
float a=heptagonal(N); //store the answer in a variable
N=13;
float b=heptagonal(N);
cout<<a<<endl<<b<<endl; //print the answer
return 0;
}
55
403
Nach dem Login kopieren
55 403
Zeitliche Komplexität: O(1), weil es nur konstante Zeit benötigt.
Raumkomplexität: O(1), da kein zusätzlicher Raum verwendet wird.
FazitWir haben versucht, das Konzept der siebeneckigen Zahlen und die Formel zur Berechnung der n-ten siebeneckigen Zahl zu lernen, die wir in der Methode verwendet haben.
Ich hoffe, Sie fanden diesen Artikel hilfreich beim Erlernen des Konzepts zum Drucken der n-ten siebeneckigen Zahl, die von einem beliebigen Benutzer eingegeben wurde.
Das obige ist der detaillierte Inhalt vonSiebeneckzahl. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 KI untergräbt die mathematische Forschung! Der Gewinner der Fields-Medaille und der chinesisch-amerikanische Mathematiker führten 11 hochrangige Arbeiten an | Gefällt mir bei Terence Tao
Apr 09, 2024 am 11:52 AM
KI untergräbt die mathematische Forschung! Der Gewinner der Fields-Medaille und der chinesisch-amerikanische Mathematiker führten 11 hochrangige Arbeiten an | Gefällt mir bei Terence Tao
Apr 09, 2024 am 11:52 AM
KI verändert tatsächlich die Mathematik. Vor kurzem hat Tao Zhexuan, der diesem Thema große Aufmerksamkeit gewidmet hat, die neueste Ausgabe des „Bulletin of the American Mathematical Society“ (Bulletin der American Mathematical Society) weitergeleitet. Zum Thema „Werden Maschinen die Mathematik verändern?“ äußerten viele Mathematiker ihre Meinung. Der gesamte Prozess war voller Funken, knallhart und aufregend. Der Autor verfügt über eine starke Besetzung, darunter der Fields-Medaillengewinner Akshay Venkatesh, der chinesische Mathematiker Zheng Lejun, der NYU-Informatiker Ernest Davis und viele andere bekannte Wissenschaftler der Branche. Die Welt der KI hat sich dramatisch verändert. Viele dieser Artikel wurden vor einem Jahr eingereicht.
 Entfernen Sie doppelte Werte mithilfe regulärer Ausdrücke aus dem PHP-Array
Apr 26, 2024 pm 04:33 PM
Entfernen Sie doppelte Werte mithilfe regulärer Ausdrücke aus dem PHP-Array
Apr 26, 2024 pm 04:33 PM
So entfernen Sie doppelte Werte mithilfe regulärer Ausdrücke aus einem PHP-Array: Verwenden Sie den regulären Ausdruck /(.*)(.+)/i, um Duplikate abzugleichen und zu ersetzen. Durchlaufen Sie die Array-Elemente und prüfen Sie mit preg_match, ob Übereinstimmungen vorliegen. Wenn es eine Übereinstimmung gibt, überspringen Sie den Wert; andernfalls fügen Sie ihn einem neuen Array ohne doppelte Werte hinzu.
 Der bahnbrechende CVM-Algorithmus löst Zählprobleme aus über 40 Jahren! Informatiker wirft Münze, um einzigartiges Wort für „Hamlet' zu finden
Jun 07, 2024 pm 03:44 PM
Der bahnbrechende CVM-Algorithmus löst Zählprobleme aus über 40 Jahren! Informatiker wirft Münze, um einzigartiges Wort für „Hamlet' zu finden
Jun 07, 2024 pm 03:44 PM
Zählen klingt einfach, ist aber in der Praxis sehr schwierig. Stellen Sie sich vor, Sie werden in einen unberührten Regenwald transportiert, um eine Wildtierzählung durchzuführen. Wenn Sie ein Tier sehen, machen Sie ein Foto. Digitalkameras zeichnen nur die Gesamtzahl der verfolgten Tiere auf, Sie interessieren sich jedoch für die Anzahl der einzelnen Tiere, es gibt jedoch keine Statistiken. Wie erhält man also am besten Zugang zu dieser einzigartigen Tierpopulation? An diesem Punkt müssen Sie sagen: Beginnen Sie jetzt mit dem Zählen und vergleichen Sie schließlich jede neue Art vom Foto mit der Liste. Für Informationsmengen bis zu mehreren Milliarden Einträgen ist diese gängige Zählmethode jedoch teilweise nicht geeignet. Informatiker des Indian Statistical Institute (UNL) und der National University of Singapore haben einen neuen Algorithmus vorgeschlagen – CVM. Es kann die Berechnung verschiedener Elemente in einer langen Liste annähern.
 Wozu dient das Programmieren und welchen Nutzen hat es, es zu lernen?
Apr 28, 2024 pm 01:34 PM
Wozu dient das Programmieren und welchen Nutzen hat es, es zu lernen?
Apr 28, 2024 pm 01:34 PM
1. Mithilfe der Programmierung können verschiedene Software- und Anwendungsprogramme entwickelt werden, darunter Websites, mobile Anwendungen, Spiele und Datenanalysetools. Seine Anwendungsbereiche sind sehr breit gefächert und decken nahezu alle Branchen ab, darunter wissenschaftliche Forschung, Gesundheitswesen, Finanzen, Bildung, Unterhaltung usw. 2. Das Erlernen des Programmierens kann uns helfen, unsere Fähigkeiten zur Problemlösung und unser logisches Denkvermögen zu verbessern. Beim Programmieren müssen wir Probleme analysieren und verstehen, Lösungen finden und diese in Code übersetzen. Diese Denkweise kann unsere analytischen und abstrakten Fähigkeiten fördern und unsere Fähigkeit verbessern, praktische Probleme zu lösen.
 MLP wurde über Nacht getötet! MIT Caltech und andere revolutionäre KANs brechen Rekorde und entdecken mathematische Theoreme, die DeepMind zerstören
May 06, 2024 pm 03:10 PM
MLP wurde über Nacht getötet! MIT Caltech und andere revolutionäre KANs brechen Rekorde und entdecken mathematische Theoreme, die DeepMind zerstören
May 06, 2024 pm 03:10 PM
Über Nacht wird sich das Paradigma des maschinellen Lernens ändern! Heutzutage ist die Infrastruktur, die den Bereich des Deep Learning dominiert, das Multilayer Perceptron (MLP), das Aktivierungsfunktionen auf Neuronen überträgt. Gibt es darüber hinaus irgendwelche neuen Wege, die wir einschlagen können? Erst heute haben Teams vom MIT, Caltech, der Northeastern University und anderen Institutionen eine neue neuronale Netzwerkstruktur veröffentlicht – Kolmogorov-Arnold Networks (KAN). Die Forscher haben eine einfache Änderung am MLP vorgenommen, indem sie die lernbare Aktivierungsfunktion von den Knoten (Neuronen) zu den Kanten (Gewichten) verschoben haben! Papieradresse: https://arxiv.org/pdf/2404.19756 Diese Änderung scheint auf den ersten Blick unbegründet
 Sammlung von C++-Programmierrätseln: Regen Sie das Denken an und verbessern Sie Ihre Programmierkenntnisse
Jun 01, 2024 pm 10:26 PM
Sammlung von C++-Programmierrätseln: Regen Sie das Denken an und verbessern Sie Ihre Programmierkenntnisse
Jun 01, 2024 pm 10:26 PM
C++-Programmierrätsel behandeln Algorithmen- und Datenstrukturkonzepte wie Fibonacci-Folge, Fakultät, Hamming-Distanz, Maximal- und Minimalwerte von Arrays usw. Durch das Lösen dieser Rätsel können Sie Ihre C++-Kenntnisse festigen und das Algorithmusverständnis und die Programmierkenntnisse verbessern.
 Erstellen Sie browserbasierte Anwendungen mit Golang
Apr 08, 2024 am 09:24 AM
Erstellen Sie browserbasierte Anwendungen mit Golang
Apr 08, 2024 am 09:24 AM
Erstellen Sie browserbasierte Anwendungen mit Golang. Golang kombiniert mit JavaScript, um dynamische Front-End-Erlebnisse zu erstellen. Installieren Sie Golang: Besuchen Sie https://golang.org/doc/install. Richten Sie ein Golang-Projekt ein: Erstellen Sie eine Datei mit dem Namen main.go. Verwendung von GorillaWebToolkit: Fügen Sie GorillaWebToolkit-Code hinzu, um HTTP-Anfragen zu verarbeiten. HTML-Vorlage erstellen: Erstellen Sie index.html im Unterverzeichnis „templates“, bei dem es sich um die Hauptvorlage handelt.
 Problemlösung mit Python: Erschließen Sie leistungsstarke Lösungen als Programmieranfänger
Oct 11, 2024 pm 08:58 PM
Problemlösung mit Python: Erschließen Sie leistungsstarke Lösungen als Programmieranfänger
Oct 11, 2024 pm 08:58 PM
Python unterstützt Anfänger bei der Problemlösung. Seine benutzerfreundliche Syntax, umfangreiche Bibliothek und Funktionen wie Variablen, bedingte Anweisungen und Schleifen ermöglichen eine effiziente Codeentwicklung. Von der Datenverwaltung über die Steuerung des Programmablaufs bis hin zur Ausführung wiederkehrender Aufgaben bietet Python




