Wie berechnet man studentisierte Residuen in Python?
Sep 24, 2023 pm 06:45 PMStudentisierte Residuen werden häufig in der Regressionsanalyse verwendet, um potenzielle Ausreißer in den Daten zu identifizieren. Ausreißer sind Punkte, die erheblich vom Gesamttrend der Daten abweichen und erhebliche Auswirkungen auf das angepasste Modell haben können. Durch die Identifizierung und Analyse von Ausreißern können Sie die zugrunde liegenden Muster in Ihren Daten besser verstehen und die Genauigkeit Ihrer Modelle verbessern. In diesem Artikel werfen wir einen genaueren Blick auf studentisierte Residuen und wie man sie in Python implementiert.
Was ist ein studentisiertes Residuum?
Der Begriff „studentisierte Residuen“ bezieht sich auf eine bestimmte Klasse von Residuen, deren Standardabweichung durch die Schätzung geteilt wird. Die Residuen der Regressionsanalyse beschreiben die Differenz zwischen dem beobachteten Wert der Antwortvariablen und ihrem vom Modell generierten erwarteten Wert. Um Ausreißer in den Daten zu finden, die das angepasste Modell erheblich beeinflussen könnten, wurden studentisierte Residuen verwendet.
Die folgende Formel wird üblicherweise zur Berechnung studentisierter Residuen verwendet -
studentized residual = residual / (standard deviation of residuals * (1 - hii)^(1/2))
Wobei sich „Rest“ auf die Differenz zwischen dem beobachteten Antwortwert und dem erwarteten Antwortwert bezieht, „Reststandardabweichung“ auf die Schätzung der Reststandardabweichung und „hii“ auf den Hebelfaktor für jeden Datenpunkt.
Berechnen Sie studentisierte Residuen mit Python
Das statsmodels-Paket kann zur Berechnung studentisierter Residuen in Python verwendet werden. Betrachten Sie zur Veranschaulichung Folgendes:
Grammatik
OLSResults.outlier_test()
Wobei OLSResults sich auf das lineare Modell bezieht, das mit der ols()-Methode von statsmodels angepasst wurde.
df = pd.DataFrame({'rating': [95, 82, 92, 90, 97, 85, 80, 70, 82, 83],
'points': [22, 25, 17, 19, 26, 24, 9, 19, 11, 16]})
model = ols('rating ~ points', data=df).fit()
stud_res = model.outlier_test()
Wobei sich „Bewertung“ und „Punktzahl“ auf eine einfache lineare Regression beziehen.
Algorithmus
Numpy, Pandas, Statsmodel API importieren.
Erstellen Sie einen Datensatz.
Führen Sie ein einfaches lineares Regressionsmodell für den Datensatz durch.
Berechnen Sie studentisierte Residuen.
Drucken Sie studentisierte Residuen.
Beispiel
Hier ist eine Demonstration der Verwendung der Scikit-Posthocs-Bibliothek zum Ausführen von Dunns Tests -
#import necessary packages and functions
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
#create dataset
df = pd.DataFrame({'rating': [95, 82, 92, 90, 97, 85, 80, 70, 82, 83], 'points': [22, 25, 17, 19, 26, 24, 9, 19, 11, 16]})
Als nächstes erstellen Sie ein lineares Regressionsmodell mit der OLS-Klasse statsmodels -
#fit simple linear regression model
model = ols('rating ~ points', data=df).fit()
Mit der Outlier-Test()-Methode können die studentisierten Residuen für jede Beobachtung im Datensatz in einem DataFrame generiert werden -
#calculate studentized residuals stud_res = model.outlier_test() #display studentized residuals print(stud_res)
Ausgabe
student_resid unadj_p bonf(p) 0 1.048218 0.329376 1.000000 1 -1.018535 0.342328 1.000000 2 0.994962 0.352896 1.000000 3 0.548454 0.600426 1.000000 4 1.125756 0.297380 1.000000 5 -0.465472 0.655728 1.000000 6 -0.029670 0.977158 1.000000 7 -2.940743 0.021690 0.216903 8 0.100759 0.922567 1.000000 9 -0.134123 0.897080 1.000000
Wir können Prädiktorwerte auch schnell gegen studentisierte Residuen grafisch darstellen -
Grammatik
x = df['points']
y = stud_res['student_resid']
plt.scatter(x, y)
plt.axhline(y=0, color='black', linestyle='--')
plt.xlabel('Points')
plt.ylabel('Studentized Residuals')
Hier verwenden wir die Matpotlib-Bibliothek, um das Diagramm mit Farbe = 'schwarz' und Lebensstil = '--' zu zeichnen
Algorithmus
Importieren Sie die Pyplot-Bibliothek von matplotlib
Prädiktorwerte definieren
Definieren Sie das studentisierte Residuum
Erstellen Sie ein Streudiagramm von Prädiktoren im Vergleich zu studentisierten Residuen
Beispiel
import matplotlib.pyplot as plt
#define predictor variable values and studentized residuals
x = df['points']
y = stud_res['student_resid']
#create scatterplot of predictor variable vs. studentized residuals
plt.scatter(x, y)
plt.axhline(y=0, color='black', linestyle='--')
plt.xlabel('Points')
plt.ylabel('Studentized Residuals')
Ausgabe
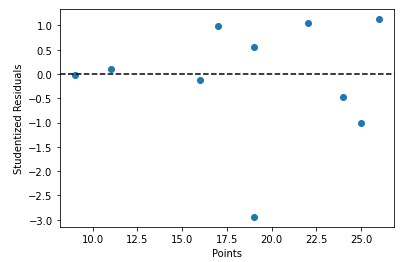
Fazit
Mögliche Datenausreißer identifizieren und bewerten. Durch die Untersuchung studentisierter Residuen können Sie Punkte finden, die erheblich vom Gesamttrend der Daten abweichen, und untersuchen, warum sie sich auf das angepasste Modell auswirken. Identifizieren signifikanter Beobachtungen Studentisierte Residuen können verwendet werden, um einflussreiche Daten zu entdecken und auszuwerten, die einen signifikanten Einfluss auf das angepasste Modell haben. Suchen Sie nach Stellen mit hoher Hebelwirkung. Studentisierte Residuen können verwendet werden, um Punkte mit hoher Hebelwirkung zu identifizieren. Die Hebelwirkung ist ein Maß dafür, wie viel Einfluss ein Punkt auf das angepasste Modell hat. Insgesamt hilft die Verwendung studentisierter Residuen dabei, die Leistung von Regressionsmodellen zu analysieren und zu verbessern.
Das obige ist der detaillierte Inhalt vonWie berechnet man studentisierte Residuen in Python?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heißer Artikel

Hot-Tools-Tags

Heißer Artikel

Heiße Artikel -Tags

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 AssertionError: Wie behebe ich Python-Assertionsfehler?
Jun 25, 2023 pm 11:07 PM
AssertionError: Wie behebe ich Python-Assertionsfehler?
Jun 25, 2023 pm 11:07 PM
AssertionError: Wie behebe ich Python-Assertionsfehler?
 So entwickeln Sie einen Schwachstellenscanner in Python
Jul 01, 2023 am 08:10 AM
So entwickeln Sie einen Schwachstellenscanner in Python
Jul 01, 2023 am 08:10 AM
So entwickeln Sie einen Schwachstellenscanner in Python
 Stratifizierte Stichprobentechniken in Python
Jun 10, 2023 pm 10:40 PM
Stratifizierte Stichprobentechniken in Python
Jun 10, 2023 pm 10:40 PM
Stratifizierte Stichprobentechniken in Python
 So verwenden Sie Python für die Skripterstellung und Ausführung unter Linux
Oct 05, 2023 am 11:45 AM
So verwenden Sie Python für die Skripterstellung und Ausführung unter Linux
Oct 05, 2023 am 11:45 AM
So verwenden Sie Python für die Skripterstellung und Ausführung unter Linux
 Verwendung der Funktion sqrt() in Python
Feb 21, 2024 pm 03:09 PM
Verwendung der Funktion sqrt() in Python
Feb 21, 2024 pm 03:09 PM
Verwendung der Funktion sqrt() in Python
 Wie verwende ich die Support-Vektor-Clustering-Technik in Python?
Jun 06, 2023 am 08:00 AM
Wie verwende ich die Support-Vektor-Clustering-Technik in Python?
Jun 06, 2023 am 08:00 AM
Wie verwende ich die Support-Vektor-Clustering-Technik in Python?
 Bringen Sie Ihnen bei, wie Sie mithilfe der Python-Programmierung das Andocken der Baidu-Bilderkennungsschnittstelle und die Bilderkennungsfunktion realisieren.
Aug 25, 2023 pm 03:10 PM
Bringen Sie Ihnen bei, wie Sie mithilfe der Python-Programmierung das Andocken der Baidu-Bilderkennungsschnittstelle und die Bilderkennungsfunktion realisieren.
Aug 25, 2023 pm 03:10 PM
Bringen Sie Ihnen bei, wie Sie mithilfe der Python-Programmierung das Andocken der Baidu-Bilderkennungsschnittstelle und die Bilderkennungsfunktion realisieren.








