Mathematisches Denken ist eine wichtige Fähigkeit moderner großer Sprachmodelle (LLM). Trotz einiger jüngster Fortschritte in diesem Bereich besteht immer noch eine deutliche Lücke zwischen Closed-Source- und Open-Source-LLM. Closed-Source-Modelle wie GPT-4, PaLM-2 und Claude 2 dominieren bei gängigen Benchmarks für mathematisches Denken wie GSM8K und MATH, während Open-Source-Modelle wie Llama, Falcon und OPT bei allen Benchmarks deutlich zurückbleiben
Um dieses Problem zu lösen, arbeitet die Forschungsgemeinschaft in zwei Richtungen:
(1) Kontinuierliche Vortrainingsmethoden wie Galactica und MINERVA können LLM kontinuierlich auf der Grundlage von mehr als 100 Milliarden mathematikbezogenen Netzwerkdaten trainieren. Diese Methode kann die allgemeine wissenschaftliche Argumentationsfähigkeit des Modells verbessern, aber der Rechenaufwand ist höher
Rejection Sampling Fine-Tuning (RFT) und spezifische Datensatz-Feinabstimmungsmethoden wie WizardMath, das überwachte Daten aus einem bestimmten Datensatz verwendet zur Feinabstimmung des LLM. Obwohl diese Methoden die Leistung innerhalb eines bestimmten Bereichs verbessern können, lassen sie sich nicht auf umfassendere mathematische Denkaufgaben über die Feinabstimmung von Daten hinaus verallgemeinern. Beispielsweise können RFT und WizardMath die Genauigkeit bei GSM8K (eines davon ist ein fein abgestimmter Datensatz) um mehr als 30 % verbessern, beeinträchtigen jedoch die Genauigkeit bei Datensätzen außerhalb der Domäne wie MMLU-Math und AQuA, wodurch sie niedriger ist bis zu 10 %
Kürzlich haben Forschungsteams von Institutionen wie der University of Waterloo und der Ohio State University eine leichte, aber verallgemeinerbare Methode zur Feinabstimmung des mathematischen Unterrichts vorgeschlagen, die verwendet werden kann, um die Allgemeingültigkeit von LLM (d. h. nicht begrenzt) zu verbessern zur Feinabstimmung von Aufgaben) mathematisches Denkvermögen.
Umgeschriebener Inhalt: In der Vergangenheit war die Fokusmethode hauptsächlich die Chain of Thought (CoT)-Methode, bei der mathematische Probleme durch schrittweise Beschreibung in natürlicher Sprache gelöst werden sollen. Diese Methode ist sehr allgemein und kann auf die meisten mathematischen Disziplinen angewendet werden, es gibt jedoch einige Schwierigkeiten in Bezug auf die Rechengenauigkeit und komplexe mathematische oder algorithmische Argumentationsprozesse (wie das Lösen von Wurzeln quadratischer Gleichungen und das Berechnen von Matrixeigenwerten)
Im Vergleich Als Nächstes: Codeformat-Prompt-Entwurfsmethoden wie Program of Thought (PoT) und PAL verwenden externe Tools (z. B. Python-Interpreter), um den mathematischen Lösungsprozess erheblich zu vereinfachen. Bei diesem Ansatz wird der Rechenprozess auf einen externen Python-Interpreter verlagert, um komplexe mathematische und algorithmische Überlegungen zu lösen (z. B. das Lösen quadratischer Gleichungen mit Sympy oder das Berechnen von Matrixeigenwerten mit Numpy). PoT hat jedoch Probleme mit abstrakteren Argumentationsszenarien wie gesundem Menschenverstand, formaler Logik und abstrakter Algebra, insbesondere ohne integrierte API.
Um die Vorteile sowohl der CoT- als auch der PoT-Methoden zu berücksichtigen, führte das Team einen neuen mathematischen Hybridanweisungs-Feinabstimmungsdatensatz MathInstruct ein, der zwei Hauptmerkmale aufweist: (1) Breite Abdeckung verschiedener mathematischer Bereiche und komplexer Abschlüsse , (2) Verschmelzung von CoT- und PoT-Prinzipien
MathInstruct basiert auf sieben vorhandenen Datensätzen mathematischer Prinzipien und sechs neu zusammengestellten Datensätzen. Sie verwendeten MathInstruct, um Lama-Modelle unterschiedlicher Größe (von 7B bis 70B) zu optimieren. Sie nannten das resultierende Modell das MAmmoTH-Modell und stellten fest, dass MAmmoTH über beispiellose Fähigkeiten verfügte, wie ein mathematischer Generalist.
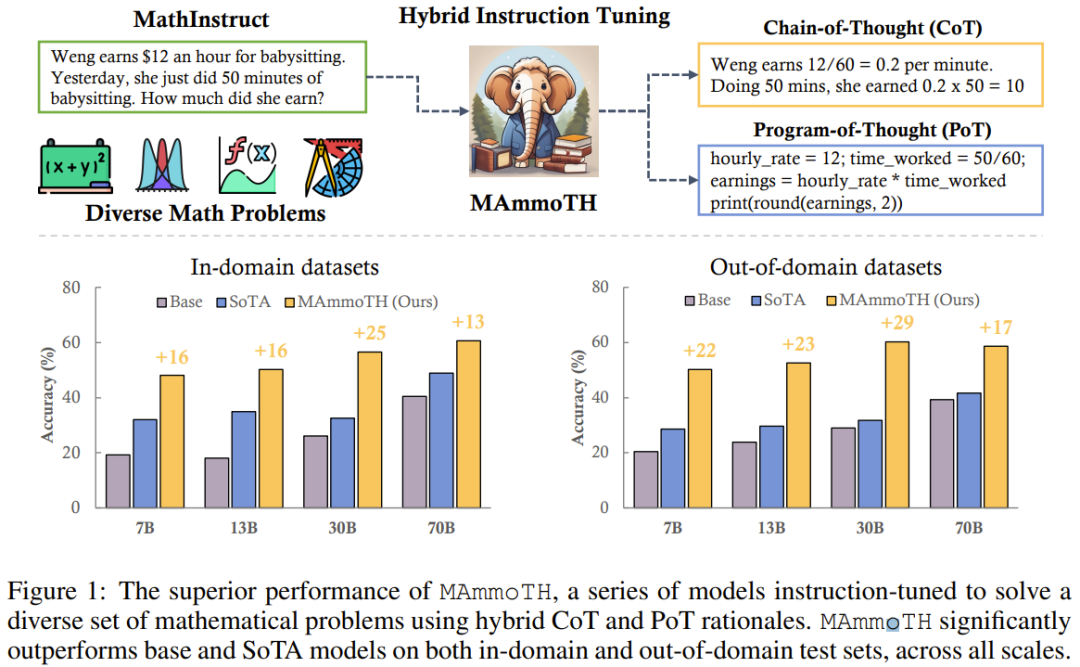
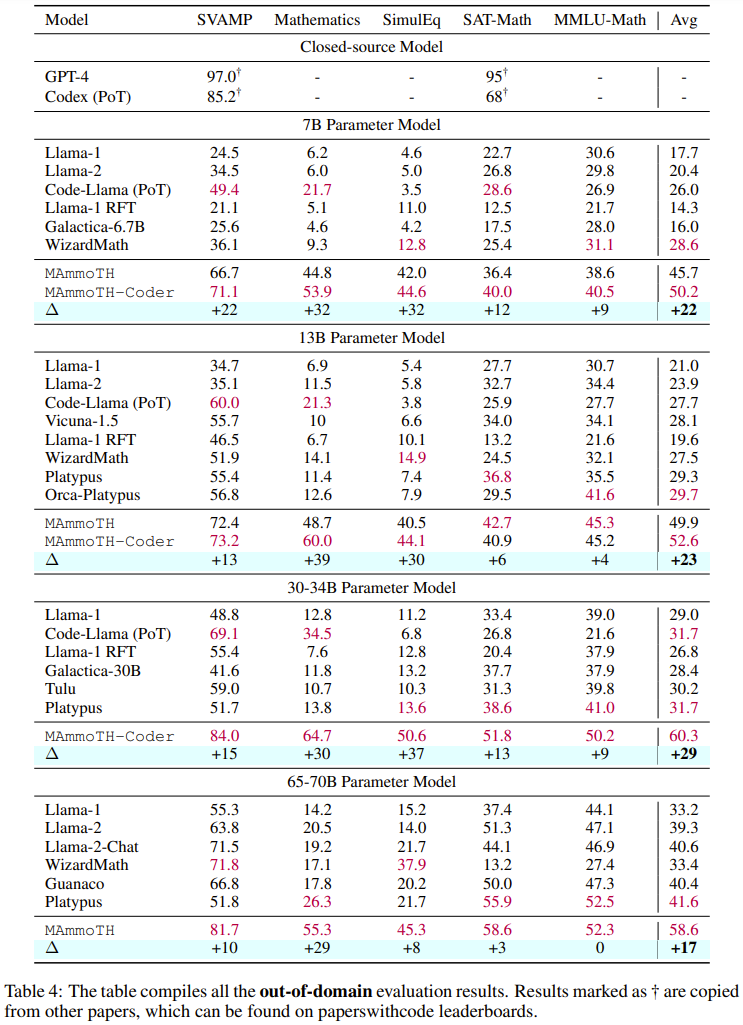
Um MAmmoTH zu bewerten, verwendete das Forschungsteam eine Reihe von Bewertungsdatensätzen, darunter Testsätze innerhalb der Domäne (GSM8K, MATH, AQuA-RAT, NumGLUE) und Testsätze außerhalb der Domäne (SVAMP, (SAT, MMLU-Math, Mathematik, SimulEq)
Forschungsergebnisse zeigen, dass das MAmmoTH-Modell bei der Verallgemeinerung auf Datensätze außerhalb der Domäne besser abschneidet und auch die Fähigkeit von Open-Source-LLM im mathematischen Denken deutlich verbessert
Es ist erwähnenswert, dass die 7B-Version von MAmmoTH im häufig verwendeten MATH-Datensatz auf Wettbewerbsebene WizardMath (das bisher beste Open-Source-Modell für MATH) um das 3,5-fache schlagen konnte (35,2 % gegenüber 10,7 %). Nach der Feinabstimmung kann der 34B MAmmoTH-Coder mithilfe von CoT sogar GPT-4 übertreffen Feinabstimmungsdatensatz, der eine Vielzahl unterschiedlicher mathematischer Probleme und Mischprinzipien enthält. (2) Im Hinblick auf die Modellierung trainierten und bewerteten sie mehr als 50 verschiedene neue Modelle und Basismodelle mit einer Größe von 7B bis 70B, um die Auswirkungen verschiedener Datenquellen und Eingabe-Ausgabe-Formate zu untersuchen
Die Forschungsergebnisse zeigen das , Neue Modelle wie MAmmoTH und MAmmoTH-Coder übertreffen bisherige Open-Source-Modelle in puncto Genauigkeit deutlich
Das Team hat den von ihnen zusammengestellten Datensatz veröffentlicht und den Code der neuen Methode als Open Source bereitgestellt und auf Hugging Face veröffentlicht Gleichzeitig möchte das Team eine Liste hochwertiger und vielfältiger Feinabstimmungsdatensätze für Mathematikunterricht erstellen, die zwei Hauptmerkmale aufweisen sollten: (1) verschiedene mathematische Bereiche und Komplexitätsstufen weitgehend abdecken und (2) CoT- und PoT-Prinzipien kombinieren.
Für Das zweite Merkmal, die Kombination von CoT- und PoT-Prinzipien, kann die Vielseitigkeit des Datensatzes verbessern und die von ihm trainierten Modelle in die Lage versetzen, verschiedene Arten mathematischer Probleme zu lösen. Allerdings liefern die meisten vorhandenen Datensätze nur begrenzte Verfahrensbegründungen, was zu einem Ungleichgewicht zwischen CoT- und PoT-Prinzipien führt. Zu diesem Zweck nutzte das Team GPT-4, um PoT-Prinzipien für ausgewählte Datensätze zu ergänzen, darunter MATH, AQuA, GSM8K und TheoremQA. Diese GPT-4-synthetisierten Programme werden dann gefiltert, indem ihre Ausführungsergebnisse mit der von Menschen kommentierten Grundwahrheit verglichen werden, um sicherzustellen, dass nur hochwertige Prinzipien hinzugefügt werden.
Nach diesen Richtlinien erstellten sie einen neuen Datensatz MathInstruct, wie in Tabelle 1 unten beschrieben.
Es enthält 260.000 Paare (Anweisungen, Antworten), die ein breites Spektrum zentraler mathematischer Bereiche (Arithmetik, Algebra, Wahrscheinlichkeit, Analysis und Geometrie usw.) abdecken, einschließlich gemischter CoT- und PoT-Prinzipien, und verfügt über unterschiedliche Sprache und Schwierigkeit.
Reset-Training
Alle Teilmengen von MathInstruct sind in einer Struktur vereinheitlicht, die dem Befehlsdatensatz von Alpaca ähnelt. Diese Normalisierungsoperation stellt sicher, dass das resultierende fein abgestimmte Modell die Daten konsistent verarbeiten kann, unabhängig vom Format des ursprünglichen Datensatzes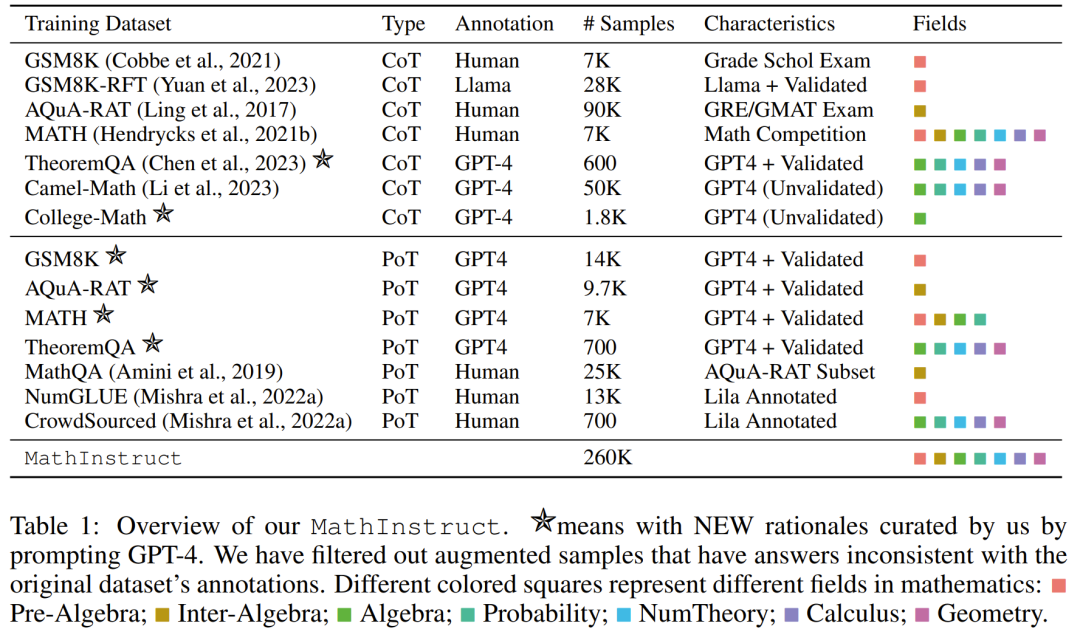 
Für das Basismodell wählte das Team Llama-2 und Code Llama
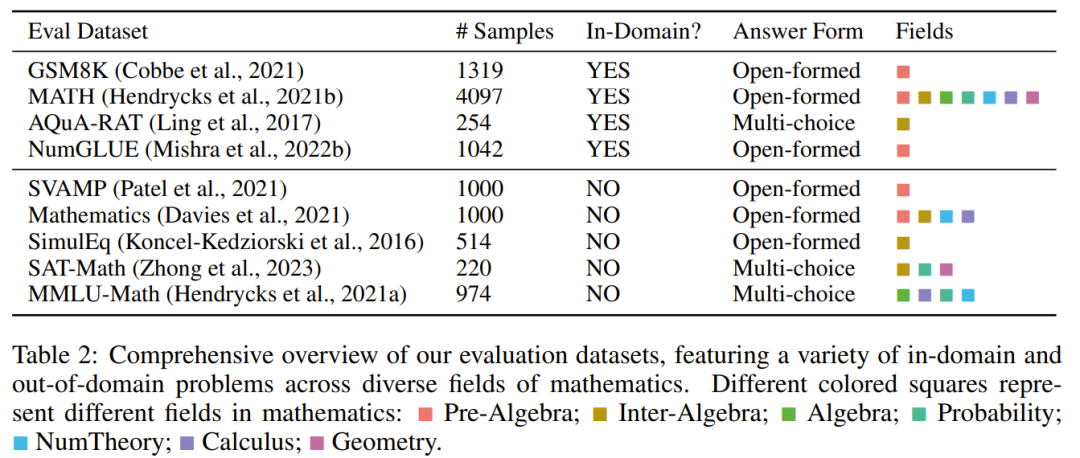
über MathInstruct Für Anpassungen erhielten sie Modelle unterschiedlicher Größe, darunter 7B, 13B, 34B und 70B Der Satz, siehe Tabelle 2 unten, enthält viele verschiedene In-Field- und Out-of-Field-Stichproben, die mehrere verschiedene Bereiche der Mathematik abdecken.
Der Bewertungsdatensatz enthält verschiedene Schwierigkeitsgrade, darunter Primar-, Sekundar- und Universitätsniveau. Einige Datensätze umfassen auch formale Logik und logisches Denken.
Die ausgewählten Bewertungsdatensätze enthalten sowohl offene als auch Multiple-Choice-Fragen.
Für Multiple-Choice-Fragen (wie AQuA und MMLU) haben die Forscher die CoT-Dekodierung übernommen, da die meisten Fragen in diesem Datensatz von CoT besser bearbeitet werden können. Für die CoT-Dekodierung sind keine Triggerwörter erforderlich, während für die PoT-Dekodierung ein Triggerwort erforderlich ist: „Lassen Sie uns ein Programm schreiben, um das Problem zu lösen.“
Hauptergebnisse
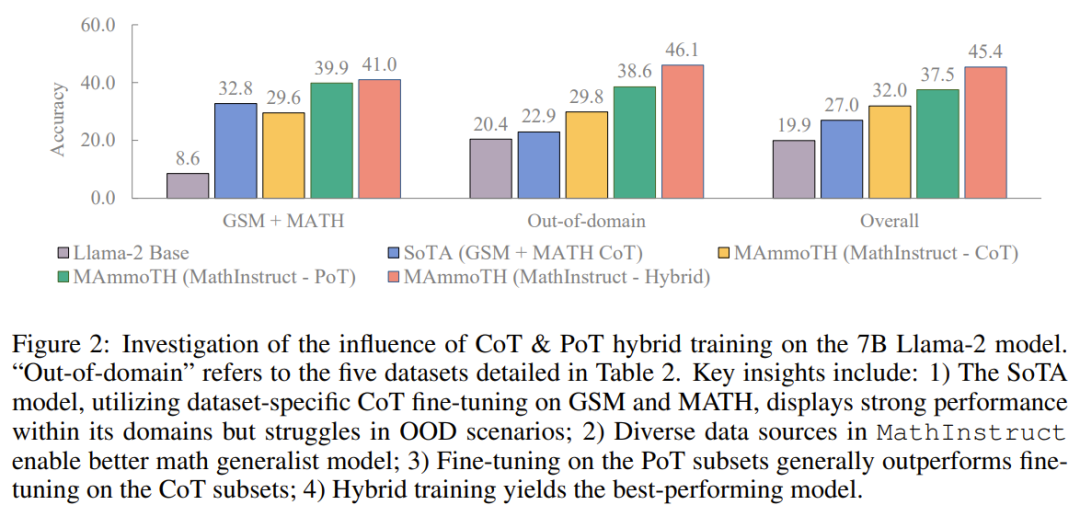
Insgesamt übertreffen sowohl MAmmoTH als auch MAmmoTH-Coder die bisherigen besten Modelle in verschiedenen Modellgrößen. Das neue Modell erzielt bei Datensätzen außerhalb der Domäne größere Leistungssteigerungen als bei Datensätzen innerhalb der Domäne. Diese Ergebnisse deuten darauf hin, dass das neue Modell das Potenzial hat, ein mathematischer Generalist zu werden. MAmmoTH-Coder-34B und MAmmoTH-70B übertreffen bei einigen Datensätzen sogar Closed-Source-LLM. Die Forscher verglichen auch mit verschiedenen Basismodellen. Konkret führten sie Experimente durch, in denen zwei Grundmodelle verglichen wurden: Llama-2 und Code-Llama. Wie aus den beiden obigen Tabellen hervorgeht, ist Code-Llama insgesamt besser als Llama-2, insbesondere bei Out-of-Field-Datensätzen. Die Lücke zwischen MAmmoTH und MAmmoTH-Coder kann sogar 5 % erreichen. Um die Quelle der Vorteile von MAmmoTH gegenüber bestehenden Benchmark-Modellen besser zu verstehen, führten die Forscher eine Reihe kontrollierter Experimente durch. Die Ergebnisse sind in Abbildung 2 dargestellt. Zusammenfassend lassen sich die erheblichen Leistungsvorteile von MAmmoTH auf Folgendes zurückführen: 1) Verschiedene Datenquellen abdecken verschiedene mathematische Bereiche und Komplexitätsstufen, 2) Hybridstrategien für die Feinabstimmung von CoT- und PoT-Unterricht. Sie untersuchten auch die Auswirkungen wichtiger Teilmengen. Im Hinblick auf die verschiedenen Quellen von MathInstruct, die zum Trainieren von MAmmoTH verwendet werden, ist es auch wichtig zu verstehen, inwieweit jede Quelle zur Gesamtleistung des Modells beiträgt. Sie konzentrieren sich auf vier Hauptuntergruppen: GSM8K, MATH, Camel und AQuA. Sie führten ein Experiment durch, bei dem jeder Datensatz nach und nach zum Training hinzugefügt wurde, und verglichen die Leistung mit einem Modell, das auf das gesamte MathInstruct abgestimmt war.
Anhand der Ergebnisse in Tabelle 5 ist ersichtlich, dass die Generalisierungsfähigkeit des Modells unzureichend ist, wenn die Diversität des Trainingsdatensatzes nicht ausreicht (z. B. wenn nur GSM8K vorhanden ist). sehr schlecht: Das Modell kann sich nur an Situationen innerhalb der Datenverteilung anpassen, es ist schwierig, Probleme über GSM-Probleme hinaus zu lösen Der wichtige Einfluss verschiedener Datenquellen auf MAmmoTH wird in diesen Ergebnissen hervorgehoben, was auch der Kernschlüssel dafür ist MAmmoTH zu einem mathematischen Generalisten machen. Diese Ergebnisse liefern auch wertvolle Erkenntnisse und Orientierungshilfen für unsere zukünftigen Datenkurations- und -erfassungsbemühungen. Beispielsweise sollten wir immer vielfältige Daten sammeln und vermeiden, nur bestimmte Datentypen zu sammeln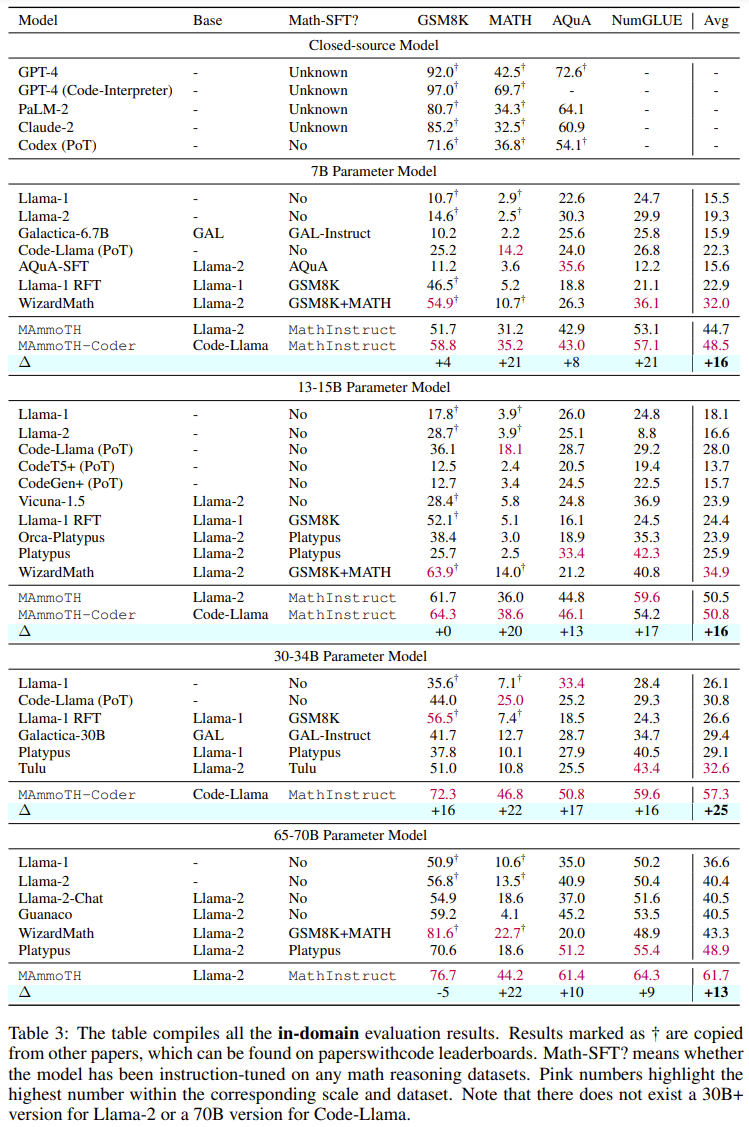 
Das obige ist der detaillierte Inhalt vonDurch MAmmoT wird LLM zum mathematischen Generalisten: von der formalen Logik bis zu vier arithmetischen Operationen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
