Sehen Sie sich Turings Prinzip noch einmal an und spüren Sie die Kraft des Beweises durch Widerspruch

Algorithmen sind allgegenwärtig geworden und es scheint, dass es für jedes Problem, das in präzisen mathematischen Begriffen ausgedrückt werden kann, einen entsprechenden Algorithmus gibt. Dies ist jedoch nicht der Fall. Tatsächlich können einige scheinbar einfache Probleme niemals durch Algorithmen gelöst werden, wie Alan Turing, ein Pionier unter den Informatikern, vor fast einem Jahrhundert in einer Arbeit bewies das rechnerische mathematische Modell, das die moderne Informatik begründete.

Turing demonstrierte dieses bahnbrechende Ergebnis mit einer kontraintuitiven Strategie: Er definierte ein Problem, eines, das alle Lösungsversuche ablehnt. „Wenn ich Sie zum Beispiel frage, was Sie tun, werde ich unabhängig von Ihrer Antwort sagen: ‚Was ich tun werde, unterscheidet sich von dem, was Sie gesagt haben‘“, sagte Rahul Ilango, ein Doktorand am MIT, der studiert Theoretische Informatik. Umgeschriebener Inhalt: Turing demonstrierte dieses bahnbrechende Ergebnis mit einer kontraintuitiven Strategie: Er definierte ein Problem, das allen Lösungsversuchen widerstand. „Wenn ich Sie zum Beispiel frage, was Sie tun, werde ich unabhängig von Ihrer Antwort sagen: ‚Was ich tun werde, unterscheidet sich von dem, was Sie gesagt haben.‘“, sagte Rahul Ilango, ein Doktorand, der theoretische Computerwissenschaften studiert Wissenschaft am MIT

Turings Strategie basiert auf einer seit langem bewährten mathematischen Methode, die als „Diagonalbeweis“ bekannt ist. Hier ist eine vereinfachte Erklärung der Logik hinter seinem Beweis

Strings

Der Diagonalbeweis beruht auf einem cleveren Trick zur Lösung eines Problems über Strings, bei dem jedes Bit einen Wert von 0 oder 1 haben kann. Die Beschreibung des Problems lautet: Bei einer gegebenen Liste von Zeichenfolgen sind alle Zeichenfolgen in der Liste gleich lang. Wie können Sie eine neue Zeichenfolge generieren, die nicht in der Liste enthalten ist?

Umgeschriebener Inhalt: Eine der einfachsten Strategien besteht darin, jede mögliche Zeichenfolge der Reihe nach zu betrachten. Angenommen, es gibt fünf Zeichenfolgen mit jeweils fünf Bits. Führen Sie zunächst eine Iteration durch, um zu prüfen, ob 00000 in der Liste vorhanden ist. Wenn es nicht existiert, ist das Problem gelöst; wenn es existiert, gehen Sie zu 00001 und wiederholen Sie den Vorgang. Dieser Ansatz ist einfach, aber langsam für lange Listen, die aus langen Strings resultieren.

Diagonal erweist sich als praktikable Alternative für den schrittweisen Aufbau nicht vorhandener Strings. Beginnen Sie mit dem ersten Bit der ersten Zeichenfolge in der Liste und kehren Sie es um. Dies wird zum ersten Bit der neuen Zeichenfolge. Kehren Sie dann das zweite Bit der zweiten Zeichenfolge um und verwenden Sie es als zweites Bit der neuen Zeichenfolge. Wiederholen Sie dies, bis Sie das Ende der Liste erreicht haben. Durch Umkehren der Bitoperationen stellen Sie sicher, dass sich die neue Zeichenfolge um mindestens eine Position von jeder Zeichenfolge in der ursprünglichen Liste unterscheidet. (Sie bilden auch eine Diagonale in der Liste der Zeichenfolgen, daher der Name Diagonalbeweis.)

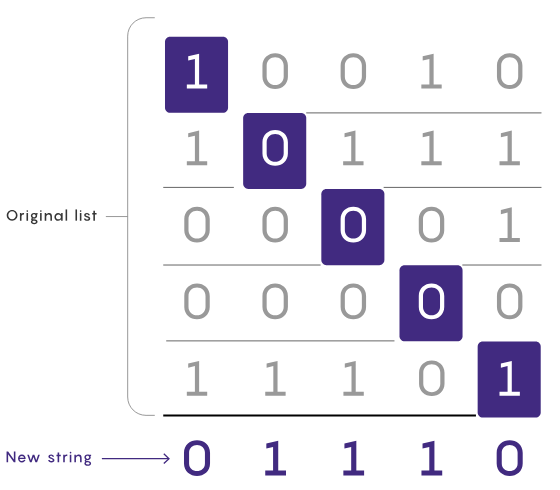Der Diagonalbeweis erfordert nur die Prüfung eines Bits von jeder Zeichenfolge in der Liste nacheinander, ist also normalerweise viel schneller als andere Methoden, aber Seine wahre Stärke liegt darin, wie gut es Probleme mit unendlich langen Saiten bewältigt.

Der theoretische Informatiker Ryan Williams vom MIT sagte: „Obwohl Zeichenfolgen und Listen unendlich sein können, ist die Diagonalisierungsmethode immer noch effektiv.“

George Cantor war der Erste, der dies ausnutzte. Er war ein Mann mit Macht und der Begründer des Fachgebiets der Mengenlehre-Mathematik. 1873 zeigte er mithilfe von Diagonalen, dass einige unendliche Werte größer sind als andere. 60 Jahre später wandte Turing diese Version des Diagonalbeweises auf die Berechnungstheorie an

Die Grenzen von Algorithmen

Um zu beweisen, dass es eine Klasse mathematischer Probleme gibt, die von keinem Algorithmus gelöst werden können, schlug Turing eine Theorie vor. Diese Art von Problem hat klar definierte Eingaben und Ausgaben, aber keinen definierten Prozess zur Umwandlung der Eingaben in Ausgaben. Turing konzentrierte sich vor allem auf Entscheidungsprobleme und versuchte, diese nebulöse Aufgabe besser zu konkretisieren. Bei einem Entscheidungsproblem kann die Eingabe eine beliebige Zeichenfolge sein, die aus 0 und 1 besteht, und die Ausgabe kann entweder 0 oder 1 sein

Die Bestimmung, ob eine Zahl eine Primzahl ist (nur durch 1 und sich selbst teilbar), ist ein Beispiel für ein Entscheidungsproblem – – Bei einer Eingabezeichenfolge, die eine Zahl darstellt, ist die korrekte Ausgabe 1, wenn die Zahl eine Primzahl ist, und 0, wenn sie keine Primzahl ist. Ein weiteres Beispiel ist die Überprüfung von Computerprogrammen auf Syntaxfehler. Die Eingabezeichenfolgen stellen den Code verschiedener Programme dar – alle Programme können auf diese Weise dargestellt werden, da sie auf diese Weise auf dem Computer gespeichert und ausgeführt werden – die Regel lautet: Wenn der Code einen Syntaxfehler enthält, dann Ausgabe 1, wenn nicht, dann Ausgang 0.

Nur wenn ein Algorithmus für jede mögliche Eingabe die richtige Ausgabe erzeugt, kann man sagen, dass er das Problem löst – wenn er auch nur einmal versagt, handelt es sich nicht um einen allgemeinen Algorithmus zur Lösung des Problems. Typischerweise spezifiziert man ein Problem, das man lösen möchte, und versucht dann, einen Algorithmus zu finden, um es zu lösen. Turing stellte diese Logik auf den Kopf, als er nach unlösbaren Problemen suchte – er stellte sich eine unendliche Liste aller möglichen Algorithmen vor und nutzte die Diagonalisierung, um ein Puzzle zu konstruieren, das jedem Algorithmus auf der Liste entgegengesetzt war.

Stellen Sie sich bitte eine neue Frage vor, die aus 20 Fragen besteht. Anstatt von einem bestimmten Konzept auszugehen, schlägt der Beantworter der Reihe nach für jede Frage ein Beispiel für die Unzufriedenheit vor. Wenn das Spiel vorbei ist, hat der Befragte einen Satz beschrieben, der vollständig aus den Gegensätzen der Frage besteht.

Turings diagonaler Beweisprozess besteht darin, über jeden Algorithmus in einer unendlich langen Liste von Algorithmen nachzudenken: „Dieser Algorithmus kann das Problem lösen.“ „Wir wollen beweisen, dass es unberechenbar ist?“ Es ist wie ein Spielwettbewerb. Williams sagte: „Diese Methode verwandelt das ursprüngliche Problem in ein ‚unendliches Problem‘.“

Um das Spiel zu gewinnen, muss Turing eine Frage entwerfen, bei der die Antwort jedes Algorithmus negativ ist. Dies bedeutet, die spezifische Eingabe zu finden, die dazu geführt hat, dass der erste Algorithmus die falsche Antwort ausgegeben hat, eine andere Eingabe, die dazu geführt hat, dass der zweite Algorithmus fehlgeschlagen ist, und so weiter. Er fand heraus, dass diese speziellen Eingaben eine ähnliche Methode verwendeten wie Kurt Gödel vor nicht allzu langer Zeit, als er zeigte, dass selbstreferenzielle Behauptungen wie „Dieser Satz ist nicht beweisbar“ Probleme bei der Grundlagenfindung in Mathematik verursachen können.

Der Schlüssel hier ist, dass jeder Algorithmus (oder jedes Programm) als eine Folge von Nullen und Einsen dargestellt werden kann. Das bedeutet, dass ein Algorithmus, genau wie im Fehlerprüfer-Beispiel, die Codierung eines anderen Algorithmus als Eingabe verwenden kann. Im Prinzip könnte der Algorithmus sogar seine eigene Kodierung als Eingabe verwenden.

Auf diese Weise können wir ein nicht berechenbares Problem definieren, genau wie das in Turings Beweis erwähnte Problem: „Gegeben eine Eingabezeichenfolge, die den Code eines Algorithmus darstellt, wenn der Code des Algorithmus selbst als Eingabe verwendet wird, wenn der Algorithmus gibt 0 aus, lassen Sie ihn 1 ausgeben, andernfalls gibt er 0 aus. „Jeder Algorithmus, der versucht, dieses Problem zu lösen, wird bei mindestens einem Eingang eine falsche Ausgabe erzeugen, nämlich dem, der seinem eigenen Code entspricht.“ Das bedeutet, dass dieses anomale Problem von keinem Algorithmus gelöst werden kann

Was nicht bewiesen werden kann, ist der Beweis durch Widerspruch

Die Verwendung von Diagonalbeweisen durch Informatiker endet hier nicht. Im Jahr 1965 adaptierten Juris Hartmanis und Richard Stearns Turings Argumentation, um zu zeigen, dass nicht alle berechenbaren Probleme gleich sind – einige sind von Natur aus schwieriger als andere. Dieses Ergebnis begründete das Gebiet der rechnerischen Komplexitätstheorie, der Untersuchung der Schwierigkeit rechnerischer Probleme.

Die Entwicklung der Komplexitätstheorie zeigt die Grenzen von Turings Diagonalbeweis. 1975 zeigten Baker, Gill und Solovy, dass viele ungelöste Probleme der Komplexitätstheorie nicht allein durch Diagonalisierung gelöst werden konnten. Das wichtigste davon ist das berühmte P/NP-Problem, bei dem es einfach um die Frage geht, ob die Richtigkeit der Lösung in Polynomzeit verifiziert werden kann und ob sie in Polynomzeit gelöst werden kann

Die Einschränkung des Diagonalbeweises ist A direktes Ergebnis des hohen Abstraktionsniveaus, das es so kraftvoll macht. Turings Beweis beinhaltete keine nicht berechenbaren Probleme, die in der Praxis auftreten könnten – stattdessen sind Probleme eher abstrakter Natur. Andere Diagonalen sind ebenso weit von der realen Welt entfernt und können daher keine realen Probleme lösen.

Williams sagte: „Der Diagonalbeweis berührt nicht direkt das Problem selbst, genau wie ein Experiment mit einer Handschuhbox.“

Der rückläufige Trend des Diagonalbeweises zeigt, dass die Lösung des P/NP-Problems ein langer Prozess sein wird Reise. Trotz ihrer Einschränkungen bleiben Diagonalbeweise eines der wichtigsten Werkzeuge im Arsenal des Komplexitätstheoretikers. Im Jahr 2011 kombinierte Williams es mit einer Reihe anderer Techniken, um zu zeigen, dass ein eingeschränktes Rechenmodell nicht in der Lage war, einige unglaublich schwierige Probleme zu lösen – ein Ergebnis, das ein Problem löste, das Forscher 25 Jahre lang beschäftigt hatte. Obwohl dies noch lange nicht die Lösung des P/NP-Problems ist, stellt es dennoch einen bedeutenden Fortschritt dar.

Wenn Sie beweisen wollen, dass etwas unmöglich ist, unterschätzen Sie nicht die Macht der Verneinung

Originallink:

Der Inhalt, der neu geschrieben werden muss, ist: https://www.quantamagazine.org/alan- turing-and-the-power-of-negative-thinking-20230905/

Das obige ist der detaillierte Inhalt vonSehen Sie sich Turings Prinzip noch einmal an und spüren Sie die Kraft des Beweises durch Widerspruch. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!