Umgekehrtes Denken: Das neue mathematische Argumentationssprachenmodell von MetaMath trainiert große Modelle

Komplexes mathematisches Denken ist ein wichtiger Indikator für die Bewertung der Argumentationsfähigkeiten großer Sprachmodelle. Derzeit weisen die häufig verwendeten Datensätze zum mathematischen Denken eine begrenzte Stichprobengröße und eine unzureichende Problemvielfalt auf, was im Großen und Ganzen zum Phänomen der „Umkehrung des Fluchs“ führt Sprachmodelle, also ein Modell, das auf „A“ trainiert wurde. Das Sprachmodell „ist B“ kann nicht auf „B ist A“ verallgemeinert werden [1]. Die spezifische Form dieses Phänomens bei mathematischen Denkaufgaben ist: Bei einem gegebenen mathematischen Problem ist das Sprachmodell gut darin, das Problem durch Vorwärtsschlussfolgerung zu lösen, es fehlt ihm jedoch die Fähigkeit, das Problem durch Rückwärtsschlussfolgerung zu lösen. Umgekehrtes Denken kommt bei mathematischen Problemen sehr häufig vor, wie die folgenden beiden Beispiele zeigen.

1. Klassische Frage – Huhn und Kaninchen im selben Käfig

• Vorwärtsbegründung: Es gibt 23 Hühner und 12 Kaninchen im Käfig.
• Umgekehrte Argumentation: Es gibt mehrere Hühner und Kaninchen im selben Käfig. Von oben gezählt sind es 35 Köpfe und von unten gezählt sind es 94 Beine. Wie viele Hühner und Kaninchen sind im Käfig?

2. GSM8K-Problem

• Vorwärtsbegründung: James kauft 5 Packungen Rindfleisch zu je 4 Pfund. Wie viel hat er bezahlt? : James kauft x Packungen Rindfleisch zu je 4 Pfund. Wie viel hat er bezahlt? Wenn wir wissen, dass die Antwort auf die obige Frage 110 ist, welchen Wert hat die unbekannte Variable x?
• Um die Vorwärts- und Rückwärtsschlussfähigkeiten des Modells zu verbessern, haben Forscher aus Cambridge, der Hong Kong University of Science and Technology und Huawei den MetaMathQA-Datensatz vorgeschlagen, der auf zwei häufig verwendeten mathematischen Datensätzen (GSM8K und MATH) basiert. : einer mit umfassender Abdeckung und einem hochwertigen Datensatz zum mathematischen Denken. MetaMathQA besteht aus 395.000 vorwärts-inversen mathematischen Frage-Antwort-Paaren, die von einem großen Sprachmodell generiert werden. Sie optimierten LLaMA-2 am MetaMathQA-Datensatz, um MetaMath zu erhalten, ein großes Sprachmodell mit Schwerpunkt auf mathematischem Denken (vorwärts und invers), das SOTA im Datensatz zum mathematischen Denken erreichte. Der MetaMathQA-Datensatz und die MetaMath-Modelle in verschiedenen Maßstäben stehen Forschern als Open Source zur Verfügung.

Projektadresse: https://meta-math.github.io/

• Papieradresse: https://arxiv.org/abs/2309.12284
• Datenadresse: https: //huggingface.co/datasets/meta-math/MetaMathQA
• Modelladresse: https://huggingface.co/meta-math
• Codeadresse: https://github.com/meta-math/ MetaMath
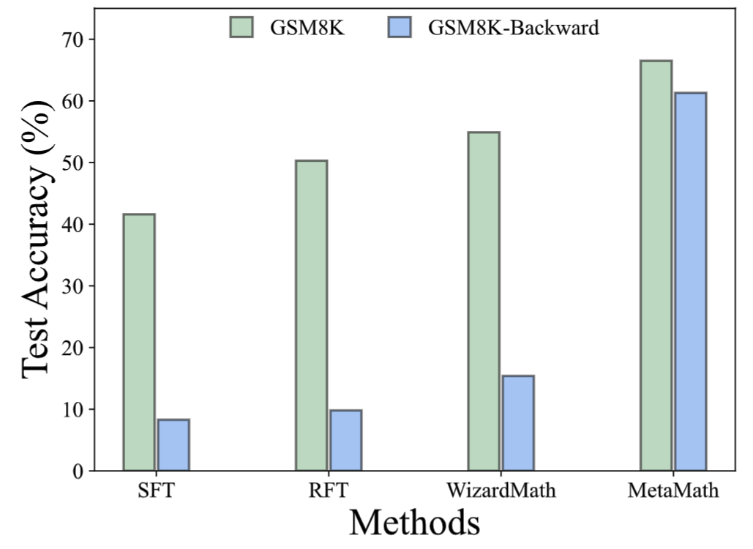
• Im GSM8K-Backward-Datensatz haben wir ein Reverse-Inference-Experiment erstellt. Experimentelle Ergebnisse zeigen, dass die aktuelle Methode im Vergleich zu Methoden wie SFT, RFT und WizardMath bei inversen Inferenzproblemen eine schlechte Leistung erbringt. Im Gegensatz dazu erzielt das MetaMath-Modell sowohl bei der Vorwärts- als auch bei der Rückwärtsinferenz eine hervorragende Leistung 1. Antworterweiterung:

Bei einer Frage wird durch ein großes Sprachmodell als Datenerweiterung eine Denkkette generiert, die das richtige Ergebnis erzielen kann.

Frage: James kauft 5 Packungen Rindfleisch zu je 4 Pfund. Der Preis für Rindfleisch beträgt 5,50 $ pro Pfund.

Antwort: James kauft 5 Packungen Rindfleisch zu je 4 Pfund jeder kauft also insgesamt 5 * 4 = 20 Pfund Rindfleisch, also zahlt er 20 * 5,50 $ = 110.

2 Frage (Verbesserung des Umschreibens von Fragen):

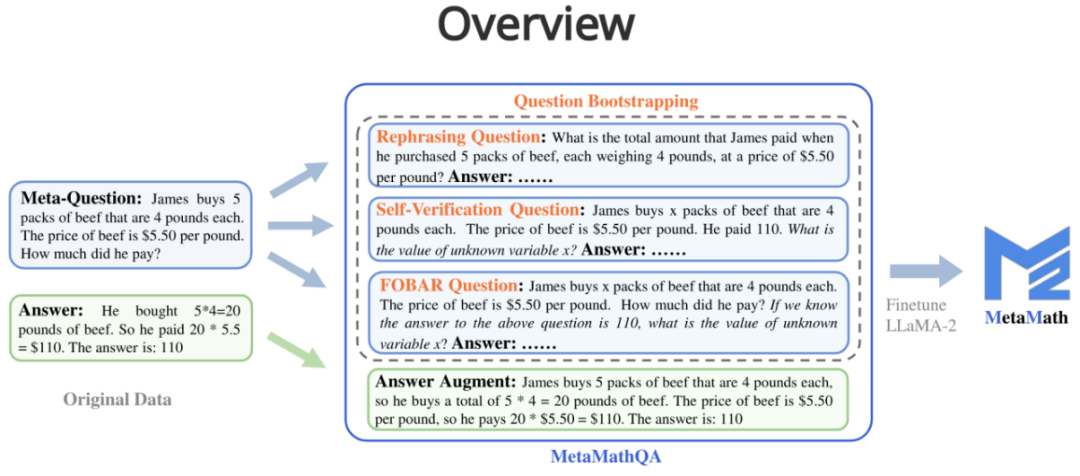
Schreiben Sie bei einer gegebenen Metafrage die Frage mithilfe eines großen Sprachmodells um und generieren Sie eine Denkkette, die als Datenerweiterung das richtige Ergebnis liefert.

• Frage: Wie hoch war der Gesamtbetrag, den James bezahlt hat, als er 5 Packungen Rindfleisch mit einem Gewicht von je 4 Pfund zu einem Preis von 5,50 $ pro Pfund kaufte?
• Antwort: Jede Packung Rindfleisch wiegt 4 Pfund, also 5 Packungen wiegen insgesamt 4 * 5 = 20 Pfund. Der Preis für 20 Pfund beträgt also 20 * 5,50 $ = 110 $

3. FOBAR-Frage (FOBAR Inverse Question Enhancement): Bei einer Metafrage ist die Zahl in der Maskenbedingung x, bei gegebener Originalantwort und invertiertem x, um eine inverse Frage zu generieren, und basierend auf Dieses inverse Problem generiert die richtige Gedankenkette zur Durchführung einer Datenerweiterung (Beispiel für eine Inversion: „Wenn wir wissen, dass die Antwort auf die obige Frage 110 ist, welchen Wert hat dann die unbekannte Variable x?“).

• Frage: James kauft x Packungen Rindfleisch zu je 4 Pfund. Der Preis für Rindfleisch beträgt 5,50 $ pro Pfund. Wie viel hat er bezahlt? von unbekannter Variable x?
• Antwort: James kauft x Packungen Rindfleisch zu je 4 Pfund, also kauft er insgesamt 4x Pfund Rindfleisch. Der Preis für Rindfleisch beträgt 5,50 $ pro Pfund, also die Gesamtkosten für das Rindfleisch ist 5,50 * 4x = 22x. Wir gehen davon aus, dass die Gesamtkosten 110 $ betragen, also können wir schreiben: 22x = 110. Wenn wir beide Seiten durch 22 dividieren, erhalten wir: x = 5. Der Wert von x ist 5,

4. Frage zur Selbstverifizierung (Verbesserung der inversen Frage zur Selbstverifizierung): Basierend auf FOBAR wird der Teil der inversen Frage durch ein großes Sprachmodell als Aussage umgeschrieben, um eine Datenerweiterung durchzuführen (umgeschriebenes Beispiel: „Wie viel hat…“ zahlt er?“ (mit der Antwort 110) wurde umgeschrieben in „Er zahlte 110“).

• Frage: James kauft x Packungen Rindfleisch zu je 4 Pfund. Der Preis für Rindfleisch beträgt 5,50 $ pro Pfund. Wie hoch ist der Wert der unbekannten Variablen x?
• Antwort: Um dies zu lösen Problem: Wir müssen den Wert von x bestimmen, der die Anzahl der Packungen Rindfleisch darstellt, die James gekauft hat, und 5,50 US-Dollar pro Pfund kostet. Wir können die Gleichung aufstellen wie folgt: Anzahl der Rindfleischpakete * Gewicht pro Pfund * Preis pro Pfund = Gesamtbetrag x * 4 * 5,50 $ = 110 $; Um x zu isolieren, wir dividieren beide Seiten der Gleichung durch 22: 22x / 22 = $110 / 22; Die Leistung verbessert die Leistung von LLM-Quellmodellen und erfordert keine Verwendung externer Tools (z. B. Code-Interpreter). Unter ihnen erreicht unser MetaMath-7B-Modell eine Genauigkeit von 66,5 % bei GSM8K und 19,8 % bei MATH, was 11,6 % bzw. 9,1 % höher ist als die hochmodernen Modelle derselben Skala. Besonders erwähnenswert ist, dass MetaMath-70B auf GSM8K eine Genauigkeit von 82,3 % erreichte und damit GPT-3,5-Turbo übertraf. Während Daten aus nachgelagerten Aufgaben die inhärenten Fähigkeiten des während des Vortrainings erlernten Sprachmodells aktivieren. Daher wirft dies zwei wichtige Fragen auf: (i) Welche Art von Daten aktiviert latentes Wissen am effektivsten und (ii) warum ist ein Datensatz bei dieser Aktivierung besser als ein anderer?

Warum ist MetaMathQA nützlich? Die Qualität (Perplexity) der Denkkettendaten wurde verbessert

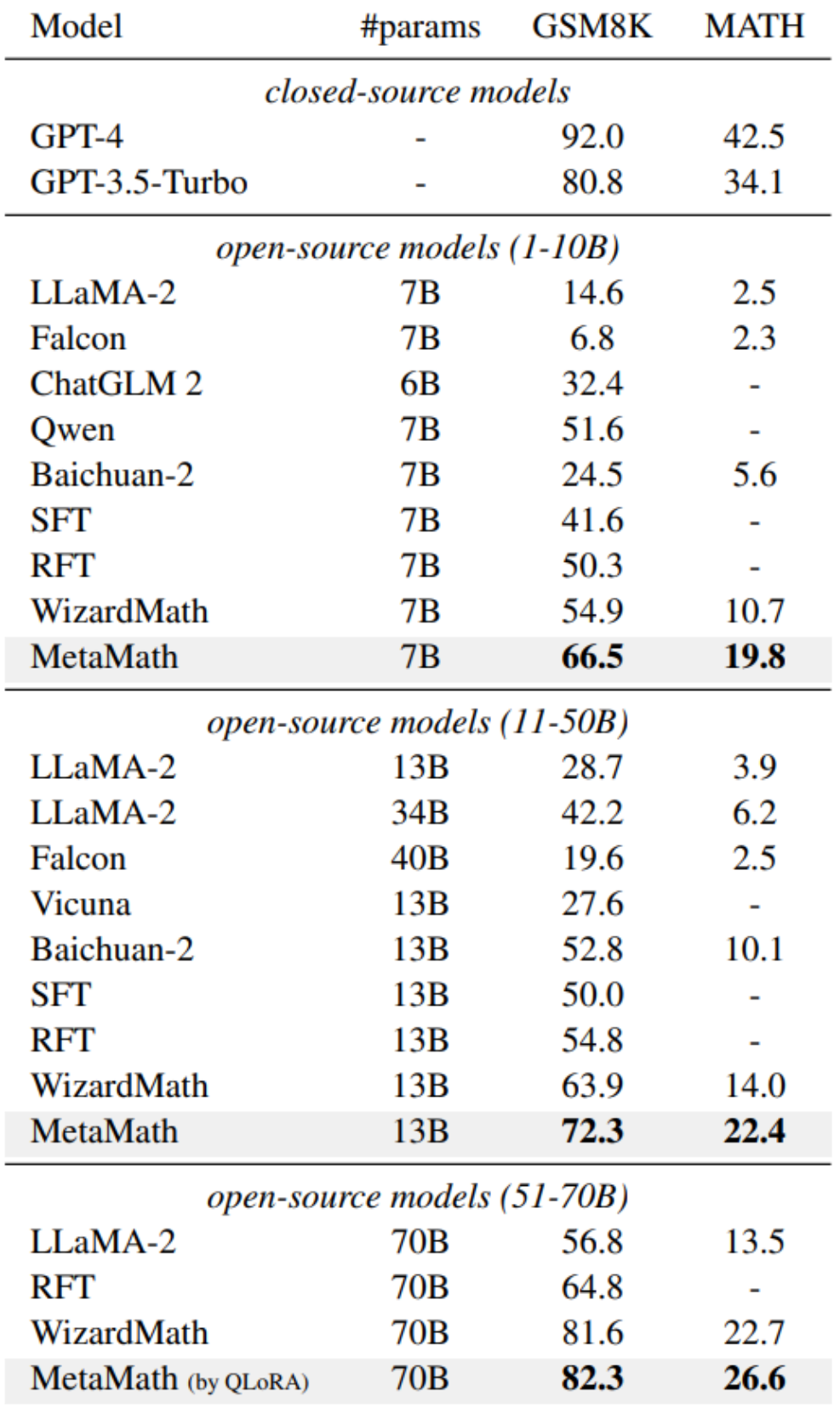
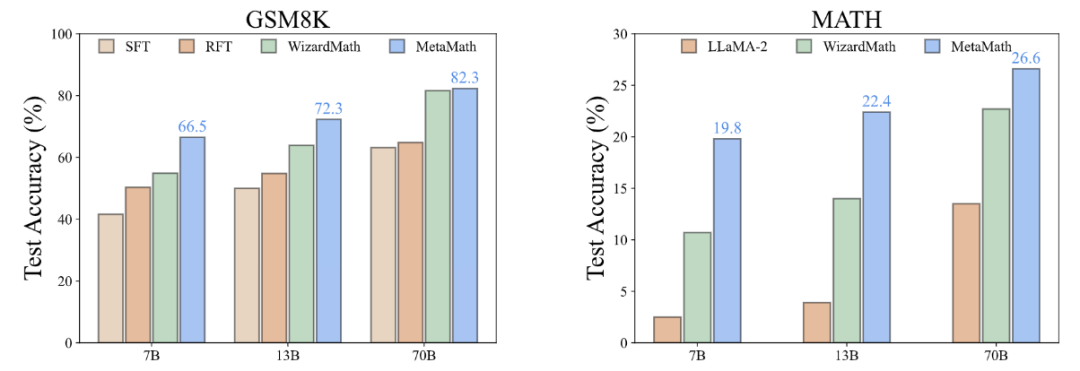
Wie in der Abbildung oben gezeigt, berechneten die Forscher das LLaMA-2-7B-Modell in jedem Teil der Nur-Antwort-Daten, GSM8K CoT und MetaMathQA-Datensätze legen den Grad der Verwirrung fest. Die Verwirrung des MetaMathQA-Datensatzes ist deutlich geringer als bei den anderen beiden Datensätzen, was darauf hindeutet, dass er eine höhere Lernfähigkeit aufweist und möglicherweise hilfreicher bei der Offenlegung des latenten Wissens des Modells ist

Warum ist MetaMathQA nützlich? Die Vielfalt der Denkkettendaten wurde erhöht

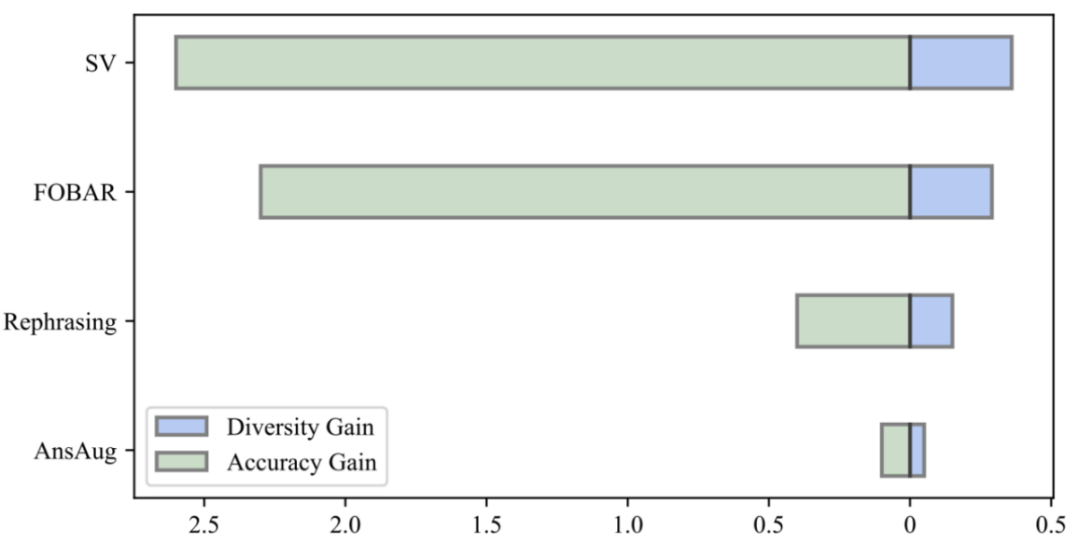
Durch den Vergleich des Diversitätsgewinns der Daten und des Genauigkeitsgewinns des Modells stellten die Forscher fest, dass die Einführung der gleichen Menge erweiterter Daten durch Neuformulierung, FOBAR und SV alle zu offensichtlichen Diversitätsgewinnen und einem deutlich verbesserten Modell führte Genauigkeit. Im Gegensatz dazu führte die alleinige Verwendung der Antworterweiterung zu einer erheblichen Sättigung der Genauigkeit. Sobald die Genauigkeit die Sättigung erreicht, führt das Hinzufügen von AnsAug-Daten nur zu einer begrenzten Leistungsverbesserung

Das obige ist der detaillierte Inhalt vonUmgekehrtes Denken: Das neue mathematische Argumentationssprachenmodell von MetaMath trainiert große Modelle. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!