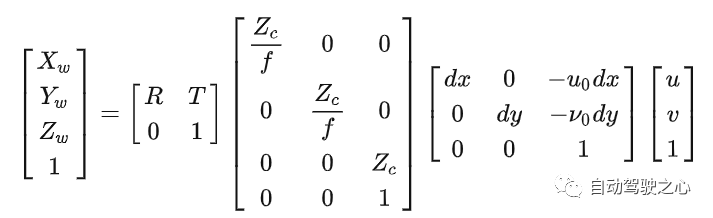Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Beherrschen Sie die Koordinatensystemkonvertierung wirklich? Multisensorik-Themen, die für das autonome Fahren unverzichtbar sind
Beherrschen Sie die Koordinatensystemkonvertierung wirklich? Multisensorik-Themen, die für das autonome Fahren unverzichtbar sind
Beherrschen Sie die Koordinatensystemkonvertierung wirklich? Multisensorik-Themen, die für das autonome Fahren unverzichtbar sind
1 Einführung und wichtige Punkte
In diesem Artikel werden hauptsächlich mehrere häufig verwendete Koordinatensysteme in der autonomen Fahrtechnologie vorgestellt und erläutert, wie die Korrelation und Konvertierung zwischen ihnen abgeschlossen und schließlich ein einheitliches Umgebungsmodell erstellt werden kann. Der Schwerpunkt liegt hier auf dem Verständnis der Umrechnung vom Fahrzeug in den starren Kamerakörper (externe Parameter), der Kamera-in-Bild-Konvertierung (interne Parameter) und der Bild-in-Pixel-Einheitenkonvertierung. Die Konvertierung von 3D in 2D führt zu entsprechenden Verzerrungen, Verschiebungen usw. Wichtiger Punkt: Selbstfahrzeugkoordinatensystem
KamerakörperkoordinatensystemWas neu geschrieben werden muss, ist: EbenenkoordinatensystemPixelkoordinatensystemSchwierigkeit: Bildverzerrung muss berücksichtigt werden, und sowohl Entverzerrung als auch Verzerrungsaddition sind erforderlich Kompensiert auf der Bildebene
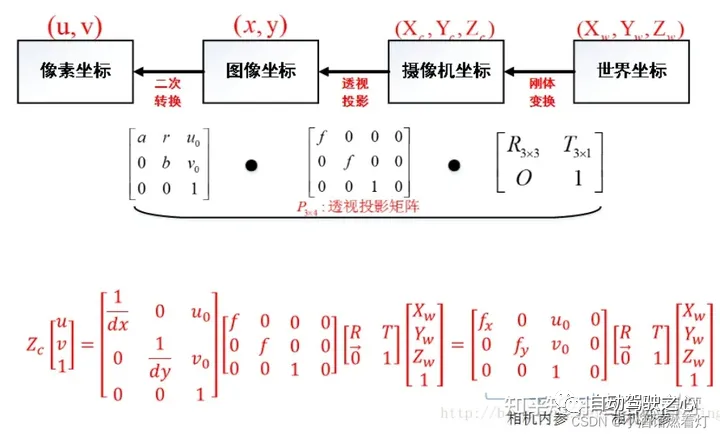
Das visuelle System hat vier Koordinatensysteme: Pixelebenenkoordinatensystem (u, v), Bildkoordinatensystem (x, y), Kamerakoordinatensystem () und Weltkoordinatensystem ( ). Es besteht eine Verbindung zwischen jedem Koordinatensystem. Daher muss durch die Kamerakalibrierung gelöst werden, wie die Koordinaten des Weltkoordinatensystems anhand der Bildpixelkoordinaten ermittelt werden können. Der Schlüsselteil des Algorithmus liegt in der Koordinatensystemkonvertierung und der Transformation erfolgt durch
Die Darstellung homogener Koordinatenerfolgt. Drei Sensorkoordinatensysteme
3.1 KamerakoordinatensystemDie Funktion der Kamera besteht darin, die Form- und Farbinformationen in der dreidimensionalen Welt in ein zweidimensionales Bild zu komprimieren
. Der kamerabasierteWahrnehmungsalgorithmus extrahiert und stellt Elemente und Informationen in der dreidimensionalen Welt aus zweidimensionalen Bildern wie Fahrspurlinien, Fahrzeugen, Fußgängern usw. wieder her und berechnet deren relative Positionen zu sich selbst. Zu den Koordinatensystemen im Zusammenhang mit dem Wahrnehmungsalgorithmus und der Kamera gehören das Bildkoordinatensystem (Pixelkoordinatensystem) und das Kamerakoordinatensystem. Was neu geschrieben werden muss, ist: das Ebenenkoordinatensystem
3.1.1 Bildkoordinatensystem (oder Pixelkoordinatensystem)
Bei auf dem Computer gespeicherten Fotos oder Bildern ist die obere linke Ecke im Allgemeinen der Ursprung, die positive x-Richtung ist nach rechts und die positive y-Richtung ist nach unten. Die am häufigsten verwendete Einheit ist „Pixel“. Das Bildkoordinatensystem ist ein zweidimensionales Koordinatensystem mit der Bezeichnung (Xv, Yv).Der Inhalt, der neu geschrieben werden muss, ist: 3.1.2 Kamerakoordinatensystem
Da die x-Achse des Bildkoordinatensystems nach rechts und die y-Achse nach unten zeigt, wird das Kamerakoordinatensystem übernommen der Mittelpunkt der optischen Hauptachse des Objektivs als Ursprung. Im Allgemeinen ist die positive Richtung die x-Achse nach rechts, die positive Richtung die y-Achse nach unten und die positive Richtung die z-Achse nach vorne. Auf diese Weise stimmen die x- und y-Richtungen mit der Richtung des Bildkoordinatensystems überein und die z-Richtung repräsentiert die Schärfentiefe. Das Kamerakoordinatensystem kann ausgedrückt werden als (Xc, Yc). Um in der Lage zu seinquantitative Beschreibung Die Abbildungsbeziehung vom dreidimensionalen Raum zum zweidimensionalen Bild, was neu geschrieben werden muss, wird in Grafiken eingeführt: das ebene Koordinatensystem. Es handelt sich um eine Übersetzung des Kamerakoordinatensystems. Der Abstand vom Mittelpunkt der optischen Achse ist gleich der Brennweite der Kamera verkleinertes invertiertes Bild auf dem Film hinter der Mitte der optischen Achse, ist die reale Bildebene (Xf, Yf). Zur Vereinfachung der Analyse und Berechnung werden wir jedoch eine virtuelle Bildebene vor der Mitte der optischen Achse einrichten. Das Bild auf der virtuellen Bildebene ist ein aufrechtes Bild und hat die gleiche Größe wie das reale invertierte Bild Es kann jedes Objekt darstellen, das durch die Kamera eingeführt wird. Die Einheit ist Meter
Weltkoordinatensystem
, Kamerakoordinatensystem , Bildkoordinatensystem und Pixelkoordinatensystem
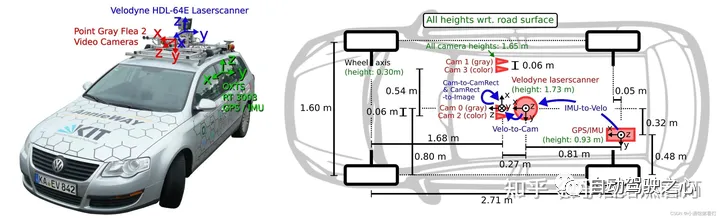
Vier Lidar-Koordinatensysteme Lidar (Light Detection and Ranging) ist ein Fernerkundungstechnologie , die mithilfe von Laserstrahlen die Entfernung zu Objekten misst. Es sendet Strahlen mit einer 360-Grad-Drehung aus und bildet elektrische Wolken basierend auf unterschiedlichen Reflexionen unterschiedlicher Zielreflektivitäten. Im Bereich des autonomen Fahrens und der Robotik wird Lidar häufig als Hauptsensor eingesetzt, um „3D-Informationen der Umgebung zu erhalten“. In den meisten Fällen ist das Lidar-Koordinatensystem rechtshändig, die spezifische Definition kann jedoch je nach Lidar-Hersteller variieren.
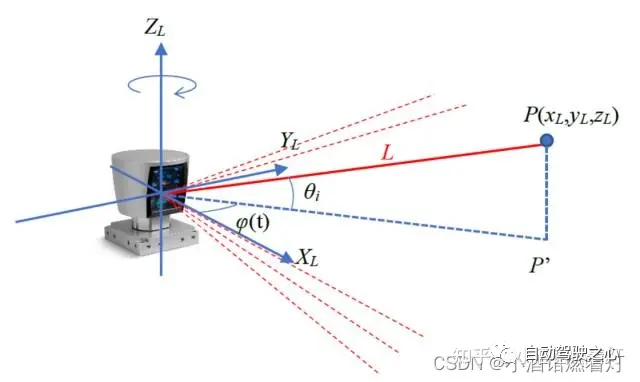
4.1 Definition
X-Achse: zeigt normalerweise vor dem Lidar. Wenn der Laserstrahl direkt nach vorne abgefeuert wird, ergibt die Entfernungsmessung aus dieser Richtung einen positiven Wert auf der X-Achse. Y-Achse: zeigt normalerweise auf die linke Seite des Lidar. Wenn der Laserstrahl direkt nach links abgefeuert wird, ergibt die Entfernungsmessung aus dieser Richtung einen positiven Wert auf der Y-Achse. Z-Achse: zeigt normalerweise nach oben vom Lidar, senkrecht zur X- und Y-Achse. Höhenmessungen werden normalerweise entlang der Z-Achse durchgeführt, wobei positive Werte anzeigen, dass das Objekt höher als das Lidar-Gerät ist, und negative Werte anzeigen, dass es niedriger als das Lidar-Gerät ist.
4.2 Bedeutung
- Das Koordinatensystem des fahrzeugmontierten Lidar-Systems stimmt möglicherweise nicht vollständig mit dem Fahrzeugkoordinatensystem überein, und eine Transformationsmatrix ist erforderlich, um eine Koordinatentransformation zwischen den beiden durchzuführen.
- Datenanmerkung, Kartenerstellung, Objekterkennung und andere Aufgaben erfordern eine klare Definition des Lidar-Koordinatensystems.
- Für die Datenfusion mit anderen Sensoren, wie z. B. Kameras, ist es sehr wichtig, die jeweiligen Koordinatensysteme zu kennen, um eine korrekte Datenausrichtung und -fusion durchzuführen.
- Bei der Datenfusion mit Kameras, Radargeräten oder anderen Sensoren ist es in der Regel erforderlich, die externen Kalibrierungsparameter (z. B. Rotations- und Translationsmatrizen) zwischen Lidar und diesen Sensoren zu kennen, um eine Koordinatentransformation zwischen ihnen durchzuführen.
Das Fünf-Fahrzeug-Koordinatensystem
Wählen Sie ein Referenzkoordinatensystem in der allgemeinen Umgebung, um die Positionen von Sensoren und Objekten zu beschreiben Dieses Koordinatensystem wird im Allgemeinen als Weltkoordinatensystem bezeichnet bezieht sich auf die Fahrzeugkarosserie Die Mitte der Hinterachse ist der Ursprung (da sich die Mitte der Hinterachse relativ zum Schwenken des Autos nicht ändert) , das räumliche Koordinatensystem oben links vorne oder oben rechts vorne, links (rechts) ist im Allgemeinen horizontal, vorne ist im Allgemeinen längs und oben bezieht sich auf den Boden. Im obigen Raum bewegt sich das Koordinatensystem mit der Bewegung des Autos. Alle Downstream-Ziele, die erfasst und ausgegeben werden müssen, müssen sich unter dem Koordinatensystem des eigenen Fahrzeugs befinden. Das BEV-Perspektivziel bezieht sich auch auf dieses Koordinatensystem.
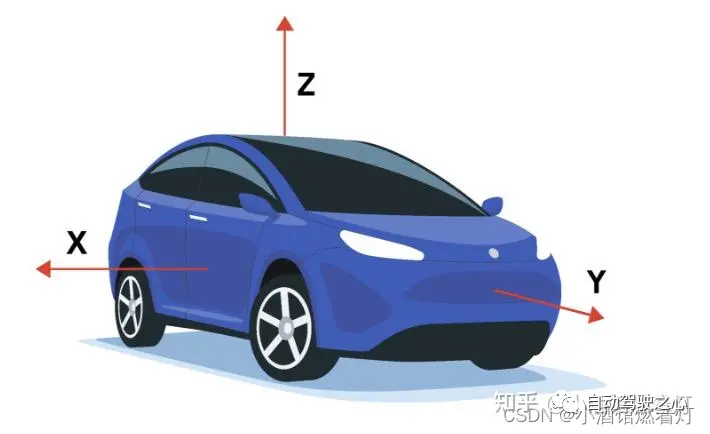
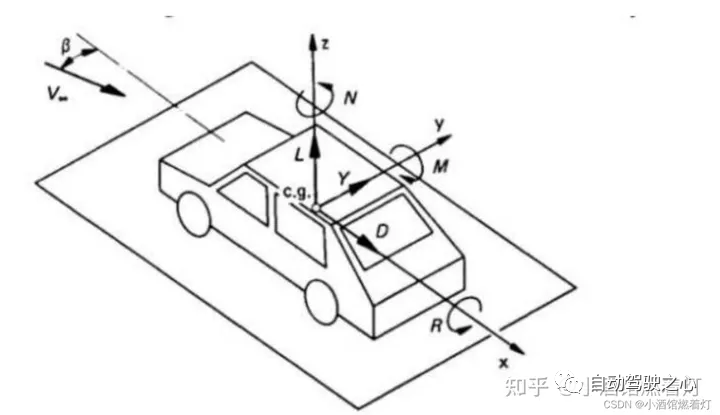
Im Allgemeinen das dreidimensionale Raumkoordinatensystem verwendet drei orthogonale Achsen Das Zeitkoordinatensystem hat nur eine Dimension. Der Einfachheit halber diskutieren wir Raumkoordinaten und Zeitkoordinaten im Allgemeinen getrennt. 6 Interne und externe Parameter der Kamera
6.1 Interne Parameter der KameraInterne Parameter werden verwendet, um das Projektionsverhältnis der Kamera vom dreidimensionalen Raum zum zweidimensionalen Bild zu bestimmen. Es enthält hauptsächlich drei Parameter:
Hauptpunkt der Kamera, Brennweite der Kamera und Verzerrungskoeffizient. Interne Parameter werden in der Regel vom Händler vorgegeben, auch eine Kamerakalibrierung kann durchgeführt werden. Bei autonomen Fahranwendungen sind die internen Parameter der Kamera Konstanten und ändern sich während der Nutzung nicht, sie müssen jedoch vor der Nutzung kalibriert werden. Der Aufnahmeprozess der Kamera kann in den Prozess der Zuordnung vom dreidimensionalen Kamerakoordinatensystem zum zweidimensionalen Koordinatensystem, dem ebenen Koordinatensystem, und anschließender Zuordnung zum Bildkoordinatensystem abstrahiert werden.
6.2 Brennweite (f) Sie beschreibt den Abstand zwischen dem Bildsensor und dem Objektiv der Kamera. Wird normalerweise durch zwei Parameter (
) und () dargestellt, die der x-Achse bzw. der y-Achse des Bildes entsprechen.
- In vielen Fällen gehen wir von (
- ) aus, was bedeutet, dass die Pixel in beide Richtungen quadratisch sind. 6.3 Hauptpunkt
- Es ist ein Punkt im Bild, normalerweise nahe der Bildmitte. Es ist der 2D-Punkt, der einem Punkt im 3D-Raum entspricht, wenn er auf die Bildebene projiziert wird. wird normalerweise durch zwei Parameter (
) und () dargestellt, die den Koordinaten auf der x-Achse und der y-Achse des Bildes entsprechen.
- 6,4 Verzerrungskoeffizient
- Das Objektiv einer echten Kamera kann zu Verzerrungen führen, die zu Bildverzerrungen führen. Zu den häufigsten Verzerrungen gehören radiale und tangentiale Verzerrungen. Der häufig verwendete radiale Verzerrungskoeffizient ist (
). Der tangentiale Verzerrungskoeffizient beträgt (
- ).
- Im Allgemeinen können die internen Parameter der Kamera durch eine Matrix dargestellt werden:
-
Diese Matrix wird oft als interne Parametermatrix oder Kameramatrix bezeichnet.
6.5 Extrinsische Parameter der Kamera
Leiten Sie die Position des Objekts im dreidimensionalen Kamerakoordinatensystem anhand des zweidimensionalen Bildes ab, z. Erhalten Sie dreidimensionale Entfernungsinformationen aus einem zweidimensionalen Bild. Wenn die Position des Objekts im Weltkoordinatensystem ermittelt werden muss, müssen Sie auch die Pose der Kamera im Weltkoordinatensystem kennen. Diese Posendarstellung wird als externer Parameter der Kamera bezeichnet und dient zur Bestimmung der relativen Positionsbeziehung zwischen den Kamerakoordinaten und dem Weltkoordinatensystem. Bei autonomen Fahranwendungen erfordert das Erhalten dieser Positionsbeziehung eine Reihe von Kalibrierungs- und Positionierungsarbeiten. Die Kamera ist eine Rotations- und Translationsmatrix relativ zu anderen Koordinatensystemen. Der externe Rotationsparameter ist der oben erwähnte Euler-Winkel [Gieren, Patch, Rollen]. Übersetzung der Kamera in das Zielkoordinatensystem. Entfernung, Einheit Meter. Sieben Fahrzeugkoordinatensysteme und Weltkoordinatensysteme Fahrzeug.
Normalerweise zeigt die X-Achse zur Vorderseite des Fahrzeugs, die Y-Achse zeigt rechts (oder links, je nach Vereinbarung) des Fahrzeugs und die Z-Achse zeigt oberhalb des Fahrzeugs.Der Ursprung dieses Koordinatensystems liegt je nach konkreter Anwendung und Konvention in der Regel an einem festen Punkt am Fahrzeug, beispielsweise in der Fahrzeugmitte, an der Hinterachse des Fahrzeugs usw.
7.2 Weltkoordinatensystem
- Dies ist ein festes, globales Koordinatensystem, das zur Beschreibung von Objekten und Fahrzeugen in der Umgebung verwendet wird.
- Der Ursprung und die Richtung des Weltkoordinatensystems werden normalerweise basierend auf der spezifischen Anwendung oder dem spezifischen Szenario ausgewählt. Es kann beispielsweise an einem festen Punkt auf einer Karte oder in der Mitte einer Szene positioniert werden.
- Das Weltkoordinatensystem bietet einen gemeinsamen Bezugsrahmen für mehrere Entitäten und ermöglicht die relative Positionierung und Navigation zwischen ihnen.
Beziehung und Konvertierung:
- - Da sich das Fahrzeug in der Welt bewegt, ändert sich die Beziehung zwischen dem eigenen Fahrzeugkoordinatensystem und dem Weltkoordinatensystem mit der Zeit. - Zur Umrechnung zwischen diesen beiden Koordinatensystemen ist in der Regel eine Transformationsmatrix bzw. Transformation (meist bestehend aus einer Drehung und einer Translation) erforderlich. Diese Konvertierung kann über verschiedene Sensoren (wie GPS, IMU, Lidar) und Algorithmen (wie SLAM) erfolgen. - Die Transformation kann als homogene 4x4-Koordinatenmatrix ausgedrückt werden, die uns die Transformation von einem Koordinatensystem in ein anderes ermöglicht.
- In den meisten Fällen sind das Koordinatensystem des eigenen Fahrzeugs und das Weltkoordinatensystem dasselbe, und dieser Artikel versteht auch dies
8.1 Vom Weltkoordinatensystem zu Das Kamerakoordinatensystem
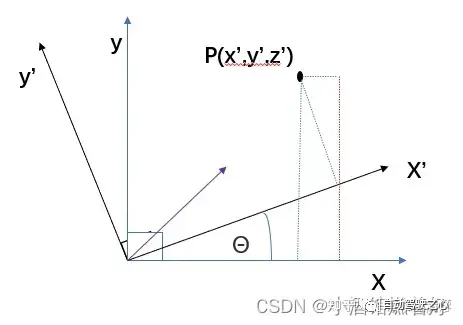
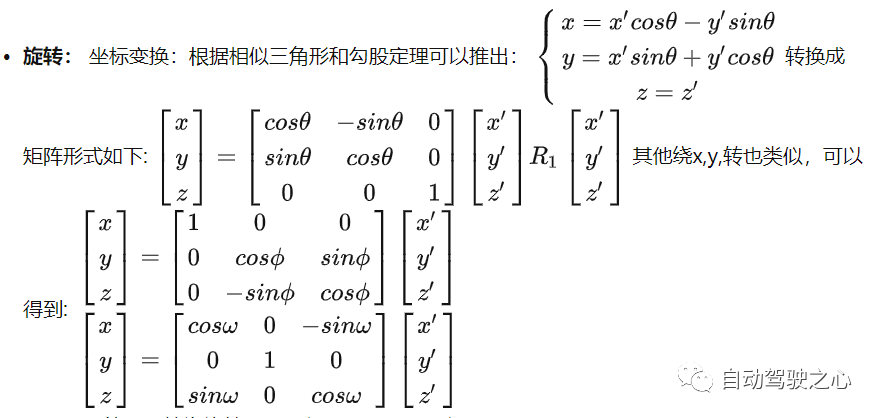
Die Koordinatensystemtransformation zwischen Objekten kann die Rotationstransformation plus Translationstransformation des Koordinatensystems darstellen, und das Gleiche gilt für die Konvertierungsbeziehung vom Weltkoordinatensystem zum Kamerakoordinatensystem. Das Drehen verschiedener Winkel um verschiedene Achsen führt zu unterschiedlichen Rotationsmatrizen.
Schematisches Diagramm der Drehung θ um die Z-Achse:Schließlich kann es einfach als Rotationsmatrix zusammengefasst werden: Übersetzung: Übersetzen Sie den Kamerakoordinatenpunkt () Der Übersetzungsabstand beträgt () zu der Weltkoordinatenpunkt
8.2 Kamerakoordinatensystem zum Bildkoordinatensystem
Vom Kamerakoordinatensystem zum Bildkoordinatensystem handelt es sich um eine perspektivische Projektionsbeziehung, die von 3D in 2D konvertiert wird. Es kann auch als Änderungsmodell des Lochblendenmodells angesehen werden. Erfüllen Sie den Dreiecksähnlichkeitssatz.
 8.3 Bildkoordinatensystem zu Pixelkoordinatensystem
8.3 Bildkoordinatensystem zu Pixelkoordinatensystem In diesem Fall gibt es im Gegensatz zur vorherigen Koordinatensystemtransformation zu diesem Zeitpunkt keine Rotationstransformation, aber die Position und Größe des Koordinatenursprungs sind inkonsistent, daher Teleskopdesign ist erforderlich. Transformation und Übersetzungstransformation
8.4 Die Beziehung zwischen den vier Koordinatensystemen


Durch die endgültige Konvertierungsbeziehung kann ein dreidimensionaler Koordinatenpunkt den entsprechenden Pixelpunkt im Bild finden. Umgekehrt wird es jedoch zu einem Problem, den entsprechenden Punkt im dreidimensionalen Raum durch einen Punkt im Bild zu finden, da wir den Wert auf der linken Seite der Gleichung nicht kennen

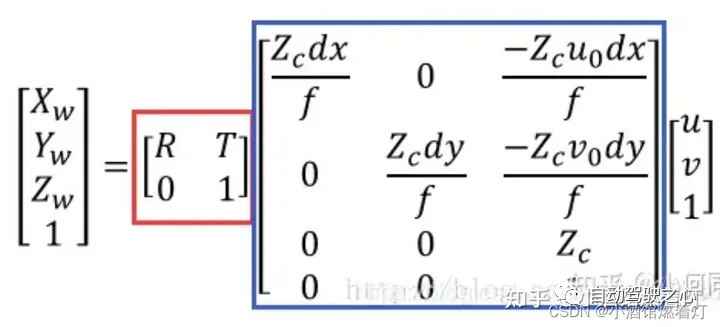
Der rote Kasten ist der Externer Parameter, R und T sind die Rotations- bzw. Translationsbeträge. Die internen Parameter sind inhärente Attribute der Kamera, nämlich die Brennweite f und die Pixelgröße dx,dy. Offensichtlich stellt es den Abstand zwischen dem Punkt und der optischen Achse dar.
Neun Zusammenfassung
sortiert die verschiedenen Koordinatensysteme des autonomen Fahrens, zeigt die Beziehung zwischen den verschiedenen Koordinatensystemen des autonomen Fahrens und ermittelt schließlich die Beziehung zwischen das Pixelkoordinatensystem und das Weltkoordinatensystem.

Originallink: https://mp.weixin.qq.com/s/tTRCjZBRZcnb59nX3FRR8w
Das obige ist der detaillierte Inhalt vonBeherrschen Sie die Koordinatensystemkonvertierung wirklich? Multisensorik-Themen, die für das autonome Fahren unverzichtbar sind. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Jan 17, 2024 pm 02:57 PM
Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Jan 17, 2024 pm 02:57 PM
Oben geschrieben und persönliches Verständnis des Autors. Dreidimensionales Gaussplatting (3DGS) ist eine transformative Technologie, die in den letzten Jahren in den Bereichen explizite Strahlungsfelder und Computergrafik entstanden ist. Diese innovative Methode zeichnet sich durch die Verwendung von Millionen von 3D-Gaußkurven aus, was sich stark von der Neural Radiation Field (NeRF)-Methode unterscheidet, die hauptsächlich ein implizites koordinatenbasiertes Modell verwendet, um räumliche Koordinaten auf Pixelwerte abzubilden. Mit seiner expliziten Szenendarstellung und differenzierbaren Rendering-Algorithmen garantiert 3DGS nicht nur Echtzeit-Rendering-Fähigkeiten, sondern führt auch ein beispielloses Maß an Kontrolle und Szenenbearbeitung ein. Dies positioniert 3DGS als potenziellen Game-Changer für die 3D-Rekonstruktion und -Darstellung der nächsten Generation. Zu diesem Zweck geben wir erstmals einen systematischen Überblick über die neuesten Entwicklungen und Anliegen im Bereich 3DGS.
 Wie lässt sich das Long-Tail-Problem in autonomen Fahrszenarien lösen?
Jun 02, 2024 pm 02:44 PM
Wie lässt sich das Long-Tail-Problem in autonomen Fahrszenarien lösen?
Jun 02, 2024 pm 02:44 PM
Gestern wurde ich während des Interviews gefragt, ob ich irgendwelche Long-Tail-Fragen gestellt hätte, also dachte ich, ich würde eine kurze Zusammenfassung geben. Das Long-Tail-Problem des autonomen Fahrens bezieht sich auf Randfälle bei autonomen Fahrzeugen, also mögliche Szenarien mit geringer Eintrittswahrscheinlichkeit. Das wahrgenommene Long-Tail-Problem ist einer der Hauptgründe, die derzeit den betrieblichen Designbereich intelligenter autonomer Einzelfahrzeugfahrzeuge einschränken. Die zugrunde liegende Architektur und die meisten technischen Probleme des autonomen Fahrens wurden gelöst, und die verbleibenden 5 % der Long-Tail-Probleme wurden nach und nach zum Schlüssel zur Einschränkung der Entwicklung des autonomen Fahrens. Zu diesen Problemen gehören eine Vielzahl fragmentierter Szenarien, Extremsituationen und unvorhersehbares menschliches Verhalten. Der „Long Tail“ von Randszenarien beim autonomen Fahren bezieht sich auf Randfälle in autonomen Fahrzeugen (AVs). Randfälle sind mögliche Szenarien mit geringer Eintrittswahrscheinlichkeit. diese seltenen Ereignisse
 Kamera oder Lidar wählen? Eine aktuelle Übersicht über die Erzielung einer robusten 3D-Objekterkennung
Jan 26, 2024 am 11:18 AM
Kamera oder Lidar wählen? Eine aktuelle Übersicht über die Erzielung einer robusten 3D-Objekterkennung
Jan 26, 2024 am 11:18 AM
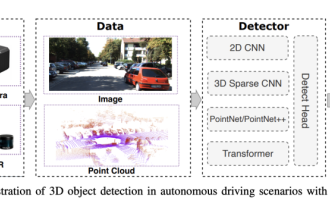
0. Vorab geschrieben&& Persönliches Verständnis, dass autonome Fahrsysteme auf fortschrittlichen Wahrnehmungs-, Entscheidungs- und Steuerungstechnologien beruhen, indem sie verschiedene Sensoren (wie Kameras, Lidar, Radar usw.) verwenden, um die Umgebung wahrzunehmen, und Algorithmen und Modelle verwenden für Echtzeitanalysen und Entscheidungsfindung. Dies ermöglicht es Fahrzeugen, Verkehrszeichen zu erkennen, andere Fahrzeuge zu erkennen und zu verfolgen, das Verhalten von Fußgängern vorherzusagen usw. und sich so sicher an komplexe Verkehrsumgebungen anzupassen. Diese Technologie erregt derzeit große Aufmerksamkeit und gilt als wichtiger Entwicklungsbereich für die Zukunft des Transportwesens . eins. Aber was autonomes Fahren schwierig macht, ist herauszufinden, wie man dem Auto klarmachen kann, was um es herum passiert. Dies erfordert, dass der dreidimensionale Objekterkennungsalgorithmus im autonomen Fahrsystem Objekte in der Umgebung, einschließlich ihrer Standorte, genau wahrnehmen und beschreiben kann.
 Das Stable Diffusion 3-Papier wird endlich veröffentlicht und die architektonischen Details werden enthüllt. Wird es helfen, Sora zu reproduzieren?
Mar 06, 2024 pm 05:34 PM
Das Stable Diffusion 3-Papier wird endlich veröffentlicht und die architektonischen Details werden enthüllt. Wird es helfen, Sora zu reproduzieren?
Mar 06, 2024 pm 05:34 PM
Der Artikel von StableDiffusion3 ist endlich da! Dieses Modell wurde vor zwei Wochen veröffentlicht und verwendet die gleiche DiT-Architektur (DiffusionTransformer) wie Sora. Nach seiner Veröffentlichung sorgte es für großes Aufsehen. Im Vergleich zur Vorgängerversion wurde die Qualität der von StableDiffusion3 generierten Bilder erheblich verbessert. Es unterstützt jetzt Eingabeaufforderungen mit mehreren Themen, und der Textschreibeffekt wurde ebenfalls verbessert, und es werden keine verstümmelten Zeichen mehr angezeigt. StabilityAI wies darauf hin, dass es sich bei StableDiffusion3 um eine Reihe von Modellen mit Parametergrößen von 800 M bis 8 B handelt. Durch diesen Parameterbereich kann das Modell direkt auf vielen tragbaren Geräten ausgeführt werden, wodurch der Einsatz von KI deutlich reduziert wird
 Dieser Artikel reicht aus, um etwas über autonomes Fahren und Flugbahnvorhersage zu lesen!
Feb 28, 2024 pm 07:20 PM
Dieser Artikel reicht aus, um etwas über autonomes Fahren und Flugbahnvorhersage zu lesen!
Feb 28, 2024 pm 07:20 PM
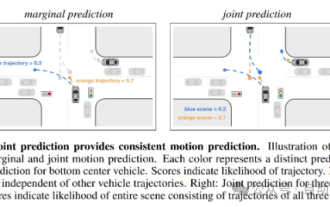
Die Trajektorienvorhersage spielt eine wichtige Rolle beim autonomen Fahren. Unter autonomer Fahrtrajektorienvorhersage versteht man die Vorhersage der zukünftigen Fahrtrajektorie des Fahrzeugs durch die Analyse verschiedener Daten während des Fahrvorgangs. Als Kernmodul des autonomen Fahrens ist die Qualität der Trajektorienvorhersage von entscheidender Bedeutung für die nachgelagerte Planungssteuerung. Die Trajektorienvorhersageaufgabe verfügt über einen umfangreichen Technologie-Stack und erfordert Vertrautheit mit der dynamischen/statischen Wahrnehmung des autonomen Fahrens, hochpräzisen Karten, Fahrspurlinien, Fähigkeiten in der neuronalen Netzwerkarchitektur (CNN&GNN&Transformer) usw. Der Einstieg ist sehr schwierig! Viele Fans hoffen, so schnell wie möglich mit der Flugbahnvorhersage beginnen zu können und Fallstricke zu vermeiden. Heute werde ich eine Bestandsaufnahme einiger häufiger Probleme und einführender Lernmethoden für die Flugbahnvorhersage machen! Einführungsbezogenes Wissen 1. Sind die Vorschaupapiere in Ordnung? A: Schauen Sie sich zuerst die Umfrage an, S
 SIMPL: Ein einfacher und effizienter Multi-Agent-Benchmark zur Bewegungsvorhersage für autonomes Fahren
Feb 20, 2024 am 11:48 AM
SIMPL: Ein einfacher und effizienter Multi-Agent-Benchmark zur Bewegungsvorhersage für autonomes Fahren
Feb 20, 2024 am 11:48 AM
Originaltitel: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Paper-Link: https://arxiv.org/pdf/2402.02519.pdf Code-Link: https://github.com/HKUST-Aerial-Robotics/SIMPL Autor: Hong Kong University of Science und Technologie DJI-Papieridee: Dieses Papier schlägt eine einfache und effiziente Bewegungsvorhersagebasislinie (SIMPL) für autonome Fahrzeuge vor. Im Vergleich zum herkömmlichen Agent-Cent
 nuScenes' neuestes SOTA |. SparseAD: Sparse-Abfrage hilft effizientes durchgängiges autonomes Fahren!
Apr 17, 2024 pm 06:22 PM
nuScenes' neuestes SOTA |. SparseAD: Sparse-Abfrage hilft effizientes durchgängiges autonomes Fahren!
Apr 17, 2024 pm 06:22 PM
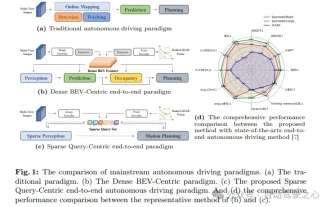
Vorab geschrieben und Ausgangspunkt Das End-to-End-Paradigma verwendet ein einheitliches Framework, um Multitasking in autonomen Fahrsystemen zu erreichen. Trotz der Einfachheit und Klarheit dieses Paradigmas bleibt die Leistung von End-to-End-Methoden für das autonome Fahren bei Teilaufgaben immer noch weit hinter Methoden für einzelne Aufgaben zurück. Gleichzeitig erschweren die in früheren End-to-End-Methoden weit verbreiteten Funktionen der dichten Vogelperspektive (BEV) die Skalierung auf mehr Modalitäten oder Aufgaben. Hier wird ein Sparse-Search-zentriertes End-to-End-Paradigma für autonomes Fahren (SparseAD) vorgeschlagen, bei dem die Sparse-Suche das gesamte Fahrszenario, einschließlich Raum, Zeit und Aufgaben, ohne dichte BEV-Darstellung vollständig abbildet. Insbesondere ist eine einheitliche, spärliche Architektur für die Aufgabenerkennung einschließlich Erkennung, Verfolgung und Online-Zuordnung konzipiert. Zudem schwer
 Sprechen wir über End-to-End- und autonome Fahrsysteme der nächsten Generation sowie über einige Missverständnisse über End-to-End-Autonomes Fahren?
Apr 15, 2024 pm 04:13 PM
Sprechen wir über End-to-End- und autonome Fahrsysteme der nächsten Generation sowie über einige Missverständnisse über End-to-End-Autonomes Fahren?
Apr 15, 2024 pm 04:13 PM
Im vergangenen Monat hatte ich aus bekannten Gründen einen sehr intensiven Austausch mit verschiedenen Lehrern und Mitschülern der Branche. Ein unvermeidliches Thema im Austausch ist natürlich End-to-End und der beliebte Tesla FSDV12. Ich möchte diese Gelegenheit nutzen, einige meiner aktuellen Gedanken und Meinungen als Referenz und Diskussion darzulegen. Wie definiert man ein durchgängiges autonomes Fahrsystem und welche Probleme sollten voraussichtlich durchgängig gelöst werden? Gemäß der traditionellsten Definition bezieht sich ein End-to-End-System auf ein System, das Rohinformationen von Sensoren eingibt und für die Aufgabe relevante Variablen direkt ausgibt. Bei der Bilderkennung kann CNN beispielsweise als End-to-End bezeichnet werden, verglichen mit der herkömmlichen Methode zum Extrahieren von Merkmalen + Klassifizieren. Bei autonomen Fahraufgaben werden Eingabedaten verschiedener Sensoren (Kamera/LiDAR) benötigt



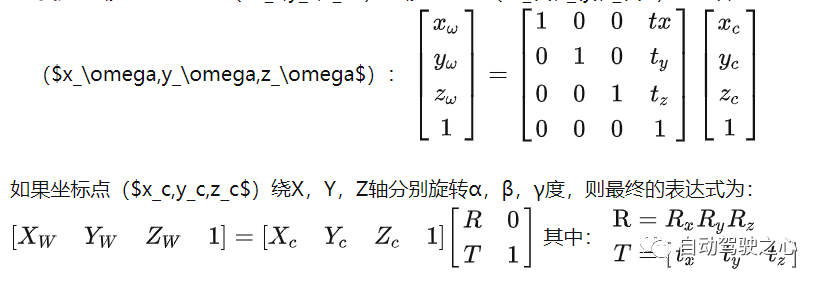 8.3 Bildkoordinatensystem zu Pixelkoordinatensystem
8.3 Bildkoordinatensystem zu Pixelkoordinatensystem