 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Terence Taos verrückter Amway-Copilot: Es hat mir geholfen, einen einseitigen Korrekturabzug zu erstellen und sogar meinen weiteren Prozess zu erraten
Terence Taos verrückter Amway-Copilot: Es hat mir geholfen, einen einseitigen Korrekturabzug zu erstellen und sogar meinen weiteren Prozess zu erraten
Terence Taos verrückter Amway-Copilot: Es hat mir geholfen, einen einseitigen Korrekturabzug zu erstellen und sogar meinen weiteren Prozess zu erraten
Nachdem Copilot von GPT-4 „unterstützt“ wurde, wurde es auch von Terence Tao bevorzugt.
Er sagte unverblümt, dass Copilot beim Programmieren direkt vorhersagen kann, was er als nächstes tun wird.
Mit Copilot ist die Forschung auch für Tao Zhexuan einfacher geworden, um seine neuesten Forschungsergebnisse zu vervollständigen.

Tao Zhexuan sagte, dass dieser Teil des Papiers eigentlich nur eine Seite hat.
Aber um diesen einseitigen Beweis zu vervollständigen, hat er mehr als 200 Zeilen Code geschrieben und dabei die neu erlernte Programmiersprache Lean4 verwendet.

Die GitHub-Seite des öffentlichen Codes von Tao Zhexuan zeigt, dass Copilot die Geschwindigkeit beim Schreiben von Code um mehr als die Hälfte erhöht hat.
Tao Zhexuan sagte, der Grund, warum er sich für Lean4 entschieden habe, sei die „Rewriting-Strategie“, die darin bestehe, einen langen Ausdruck gezielt teilweise zu ersetzen.
Wenn beispielsweise eine komplexe Funktion f(x) definiert ist und wir den Ausdruck von f(114514) eingeben möchten, können wir x mithilfe von Code direkt in 114514 „umschreiben“.
Tao Zhexuan sagte, dass diese Funktion im Vergleich zu LaTeX, das eine wiederholte Eingabe von Formeln erfordert, nicht sehr praktisch sei.
Welche neuen Ergebnisse hat uns Tao Zhexuans „One-Page Proof“ dieses Mal gebracht?
Einseitiger Beweis neuer Ungleichheiten
In diesem Artikel geht es um Probleme im Zusammenhang mit MacLaughlins Ungleichheit.
McLaughlins Ungleichung ist eine klassische Ungleichung in der Mathematik. Sie wird auf der Grundlage des Gesetzes abgeleitet, dass „das arithmetische Mittel nicht negativer reeller Zahlen größer oder gleich dem geometrischen Mittel ist“.
1...yn ist eine nicht negative reelle Zahl. Für k=1...n ist der Mittelwert Sk definiert als (der Nenner ist die Anzahl der Terme im Zähler):
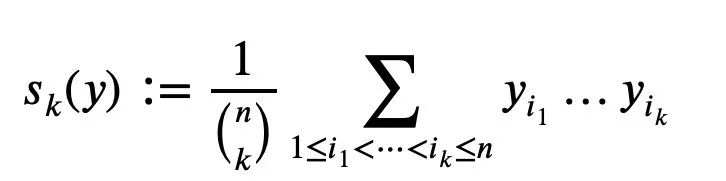 Es erscheint als normalisierter Koeffizient eines Polynoms n-ten Grades mit Wurzeln. (Denken Sie an diese Formel, wir nennen sie Formel 1)
Es erscheint als normalisierter Koeffizient eines Polynoms n-ten Grades mit Wurzeln. (Denken Sie an diese Formel, wir nennen sie Formel 1)
In der Analysis gibt es auch eine klassische Newtonsche Ungleichung:
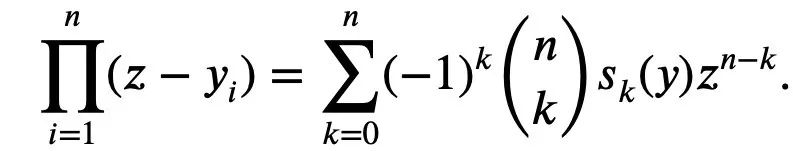
Für jedes 1≤k alle nicht negativ sind, kann Newtons Ungleichung einfach Mike beschreiben Laurins Ungleichung: Aber wenn diese Einschränkung nicht hinzugefügt wird, das heißt, die Existenz negativer Terme ist zulässig, kann Maclaurins Ungleichung nicht durch Newtons Ungleichung ausgedrückt werden. Für den Fall, dass negative Terme in Newtons Ungleichungen vorkommen können, schlug Tao Zhexuan einen neuen Satz von Ungleichungsvarianten vor: Für jedes r>0 und 1≤ℓ≤n muss Gleichung 2 oder Gleichung 3 wahr sein. Das möchte Tao Zhexuan auf dieser Seite beweisen. Der spezifische Beweisprozess ist wie folgt: Von Die vorherige Formel 1 und die Dreiecksungleichung können erhalten werden: Wir müssen also nur eine Untergrenze festlegen: Nehmen Sie den Absolutwert von P(z) und berechnen Sie dann den Logarithmus, um Folgendes zu erhalten: Da für jede reelle Zahl t, t ↦ log(e t+a) ist Konvexität und a>0, wir können die Ungleichung erhalten: Wenn a=r2, t=2log yj, können wir erhalten: The Oben ist der von Tao Zhexuan angegebene Beweisprozess dargestellt. Wenn jedoch das normalisierte |Sn|=1 gilt, gilt die folgende Formel: Zusätzlich zum „eins-“ Seitenbeweis“ dieses Mal erwähnt, Terence Taos In diesem Artikel wurde auch ein weiterer neuer Satz vorgeschlagen, nämlich für jedes 1 ≤ k ≤ ℓ≤ n.: In dem Blogbeitrag enthüllte Tao Zhexuan, dass sein nächster Plan darin besteht Schlagen Sie diese verfeinerte Version der Ungleichung vor. Tao Zhexuan sagte, dass der Beweisprozess so einfach wie das Üben sei und mit Infinitesimalrechnung durchgeführt werden könne. Allerdings erwähnte er auch, dass es eine kleine Schwierigkeit geben wird, da dieser Teil des Arguments asymptotische Symbole verwendet. Lasst uns abwarten, wie das neue Fazit aussehen wird. Tao Zhexuan ist ein treuer Fan der KI-Tools Copilot, GPT-4 und einige andere Hilfstools, die er empfohlen hat. Dieses Mal stellte er auch neue Erwartungen an die Entwicklung großer Modelle und hoffte, dass das Modell eines Tages direkt Ungleichheitsvarianten generieren kann. Papieradresse: https://arxiv.org/abs/2310.05328 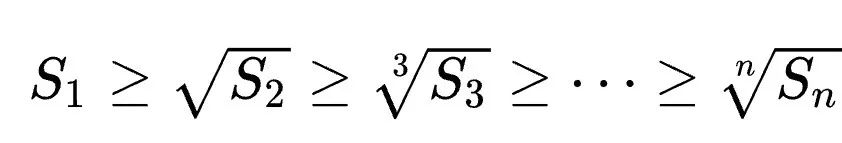
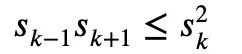
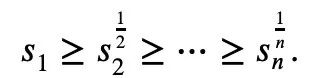
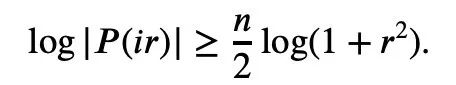
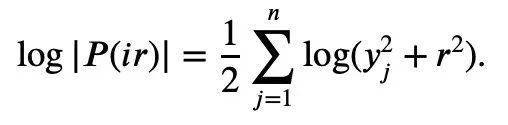
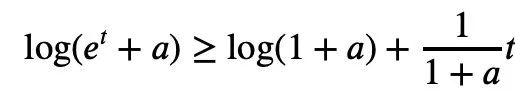
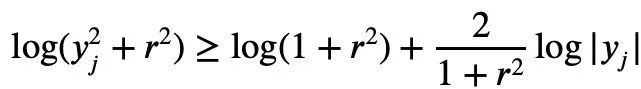
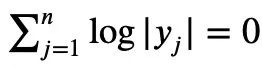
Nächster Schritt: Erstellen Sie eine verfeinerte Version
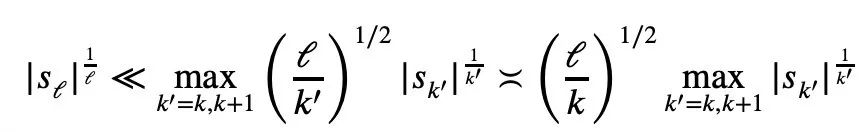

One More Thing

Das obige ist der detaillierte Inhalt vonTerence Taos verrückter Amway-Copilot: Es hat mir geholfen, einen einseitigen Korrekturabzug zu erstellen und sogar meinen weiteren Prozess zu erraten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Wie man MySQL löst, kann nicht gestartet werden
Apr 08, 2025 pm 02:21 PM
Wie man MySQL löst, kann nicht gestartet werden
Apr 08, 2025 pm 02:21 PM
Es gibt viele Gründe, warum MySQL Startup fehlschlägt und durch Überprüfung des Fehlerprotokolls diagnostiziert werden kann. Zu den allgemeinen Ursachen gehören Portkonflikte (prüfen Portbelegung und Änderung der Konfiguration), Berechtigungsprobleme (Überprüfen Sie den Dienst Ausführen von Benutzerberechtigungen), Konfigurationsdateifehler (Überprüfung der Parametereinstellungen), Datenverzeichniskorruption (Wiederherstellung von Daten oder Wiederaufbautabellenraum), InnoDB-Tabellenraumprobleme (prüfen IBDATA1-Dateien), Plug-in-Ladeversagen (Überprüfen Sie Fehlerprotokolle). Wenn Sie Probleme lösen, sollten Sie sie anhand des Fehlerprotokolls analysieren, die Hauptursache des Problems finden und die Gewohnheit entwickeln, Daten regelmäßig zu unterstützen, um Probleme zu verhindern und zu lösen.
 Kann MySQL JSON zurückgeben?
Apr 08, 2025 pm 03:09 PM
Kann MySQL JSON zurückgeben?
Apr 08, 2025 pm 03:09 PM
MySQL kann JSON -Daten zurückgeben. Die JSON_EXTRACT -Funktion extrahiert Feldwerte. Über komplexe Abfragen sollten Sie die Where -Klausel verwenden, um JSON -Daten zu filtern, aber auf die Leistungsauswirkungen achten. Die Unterstützung von MySQL für JSON nimmt ständig zu, und es wird empfohlen, auf die neuesten Versionen und Funktionen zu achten.
 Remote Senior Backend Engineers (Plattformen) benötigen Kreise
Apr 08, 2025 pm 12:27 PM
Remote Senior Backend Engineers (Plattformen) benötigen Kreise
Apr 08, 2025 pm 12:27 PM
Remote Senior Backend Engineer Job Vacant Company: Circle Standort: Remote-Büro-Jobtyp: Vollzeitgehalt: 130.000 bis 140.000 US-Dollar Stellenbeschreibung Nehmen Sie an der Forschung und Entwicklung von Mobilfunkanwendungen und öffentlichen API-bezogenen Funktionen, die den gesamten Lebenszyklus der Softwareentwicklung abdecken. Die Hauptaufgaben erledigen die Entwicklungsarbeit unabhängig von RubyonRails und arbeiten mit dem Front-End-Team von React/Redux/Relay zusammen. Erstellen Sie die Kernfunktionalität und -verbesserungen für Webanwendungen und arbeiten Sie eng mit Designer und Führung während des gesamten funktionalen Designprozesses zusammen. Fördern Sie positive Entwicklungsprozesse und priorisieren Sie die Iterationsgeschwindigkeit. Erfordert mehr als 6 Jahre komplexes Backend für Webanwendungen
 Verstehen von Säureeigenschaften: Die Säulen einer zuverlässigen Datenbank
Apr 08, 2025 pm 06:33 PM
Verstehen von Säureeigenschaften: Die Säulen einer zuverlässigen Datenbank
Apr 08, 2025 pm 06:33 PM
Detaillierte Erläuterung von Datenbanksäureattributen Säureattribute sind eine Reihe von Regeln, um die Zuverlässigkeit und Konsistenz von Datenbanktransaktionen sicherzustellen. Sie definieren, wie Datenbanksysteme Transaktionen umgehen, und sorgen dafür, dass die Datenintegrität und -genauigkeit auch im Falle von Systemabstürzen, Leistungsunterbrechungen oder mehreren Benutzern gleichzeitiger Zugriff. Säureattributübersicht Atomizität: Eine Transaktion wird als unteilbare Einheit angesehen. Jeder Teil schlägt fehl, die gesamte Transaktion wird zurückgerollt und die Datenbank behält keine Änderungen bei. Wenn beispielsweise eine Banküberweisung von einem Konto abgezogen wird, jedoch nicht auf ein anderes erhöht wird, wird der gesamte Betrieb widerrufen. begintransaktion; updateAccountsSetBalance = Balance-100WH
 Laravel eloquent orm bei bangla partieller Modellsuche)
Apr 08, 2025 pm 02:06 PM
Laravel eloquent orm bei bangla partieller Modellsuche)
Apr 08, 2025 pm 02:06 PM
Laraveleloquent-Modellab Abruf: Das Erhalten von Datenbankdaten Eloquentorm bietet eine prägnante und leicht verständliche Möglichkeit, die Datenbank zu bedienen. In diesem Artikel werden verschiedene eloquente Modellsuchtechniken im Detail eingeführt, um Daten aus der Datenbank effizient zu erhalten. 1. Holen Sie sich alle Aufzeichnungen. Verwenden Sie die Methode All (), um alle Datensätze in der Datenbanktabelle zu erhalten: UseApp \ Models \ post; $ posts = post :: all (); Dies wird eine Sammlung zurückgeben. Sie können mit der Foreach-Schleife oder anderen Sammelmethoden auf Daten zugreifen: foreach ($ postas $ post) {echo $ post->
 Master SQL Limit -Klausel: Steuern Sie die Anzahl der Zeilen in einer Abfrage
Apr 08, 2025 pm 07:00 PM
Master SQL Limit -Klausel: Steuern Sie die Anzahl der Zeilen in einer Abfrage
Apr 08, 2025 pm 07:00 PM
SQllimit -Klausel: Steuern Sie die Anzahl der Zeilen in Abfrageergebnissen. Die Grenzklausel in SQL wird verwendet, um die Anzahl der von der Abfrage zurückgegebenen Zeilen zu begrenzen. Dies ist sehr nützlich, wenn große Datensätze, paginierte Anzeigen und Testdaten verarbeitet werden und die Abfrageeffizienz effektiv verbessern können. Grundlegende Syntax der Syntax: SelectColumn1, Spalte2, ... Fromtable_Namelimitnumber_of_rows; number_of_rows: Geben Sie die Anzahl der zurückgegebenen Zeilen an. Syntax mit Offset: SelectColumn1, Spalte2, ... Fromtable_NamelimitOffset, Number_of_rows; Offset: Skip überspringen
 Der Hauptschlüssel von MySQL kann null sein
Apr 08, 2025 pm 03:03 PM
Der Hauptschlüssel von MySQL kann null sein
Apr 08, 2025 pm 03:03 PM
Der MySQL -Primärschlüssel kann nicht leer sein, da der Primärschlüssel ein Schlüsselattribut ist, das jede Zeile in der Datenbank eindeutig identifiziert. Wenn der Primärschlüssel leer sein kann, kann der Datensatz nicht eindeutig identifiziert werden, was zu Datenverwirrung führt. Wenn Sie selbstsinkrementelle Ganzzahlsspalten oder UUIDs als Primärschlüssel verwenden, sollten Sie Faktoren wie Effizienz und Raumbelegung berücksichtigen und eine geeignete Lösung auswählen.
 Wie optimieren Sie die MySQL-Leistung für Hochlastanwendungen?
Apr 08, 2025 pm 06:03 PM
Wie optimieren Sie die MySQL-Leistung für Hochlastanwendungen?
Apr 08, 2025 pm 06:03 PM
Die MySQL-Datenbankleistung Optimierungshandbuch In ressourcenintensiven Anwendungen spielt die MySQL-Datenbank eine entscheidende Rolle und ist für die Verwaltung massiver Transaktionen verantwortlich. Mit der Erweiterung der Anwendung werden jedoch die Datenbankleistung Engpässe häufig zu einer Einschränkung. In diesem Artikel werden eine Reihe effektiver Strategien zur Leistungsoptimierung von MySQL -Leistung untersucht, um sicherzustellen, dass Ihre Anwendung unter hohen Lasten effizient und reaktionsschnell bleibt. Wir werden tatsächliche Fälle kombinieren, um eingehende Schlüsseltechnologien wie Indexierung, Abfrageoptimierung, Datenbankdesign und Caching zu erklären. 1. Das Design der Datenbankarchitektur und die optimierte Datenbankarchitektur sind der Eckpfeiler der MySQL -Leistungsoptimierung. Hier sind einige Kernprinzipien: Die Auswahl des richtigen Datentyps und die Auswahl des kleinsten Datentyps, der den Anforderungen entspricht, kann nicht nur Speicherplatz speichern, sondern auch die Datenverarbeitungsgeschwindigkeit verbessern.



