11 erweiterte Visualisierungen für Datenanalyse und maschinelles Lernen

Visualisierung ist ein leistungsstarkes Werkzeug, um komplexe Datenmuster und Zusammenhänge auf intuitive und verständliche Weise zu kommunizieren. Sie spielen eine wichtige Rolle bei der Datenanalyse und liefern Erkenntnisse, die aus Rohdaten oder herkömmlichen numerischen Darstellungen oft nur schwer zu erkennen sind.

Visualisierung ist entscheidend für das Verständnis komplexer Datenmuster und -beziehungen. Wir stellen die 11 wichtigsten und unverzichtbaren Diagramme vor, die dabei helfen, die Informationen in den Daten offenzulegen und komplexe Daten verständlicher und aussagekräftiger zu machen.

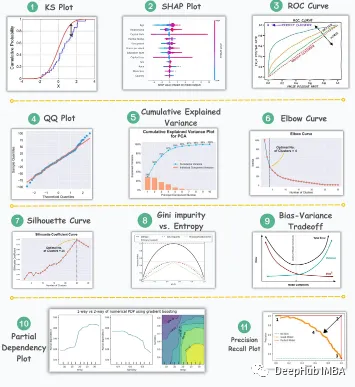
1. KS-Diagramm

KS-Diagramm wird zur Bewertung von Verteilungsunterschieden verwendet. Die Kernidee besteht darin, den maximalen Abstand zwischen den kumulativen Verteilungsfunktionen (CDF) zweier Verteilungen zu messen. Je kleiner der maximale Abstand, desto wahrscheinlicher ist es, dass sie zur gleichen Verteilung gehören. Daher wird es hauptsächlich als „statistischer Test“ zur Bestimmung der Unterschiede in den Verteilungen und nicht als „Diagramm“ interpretiert.

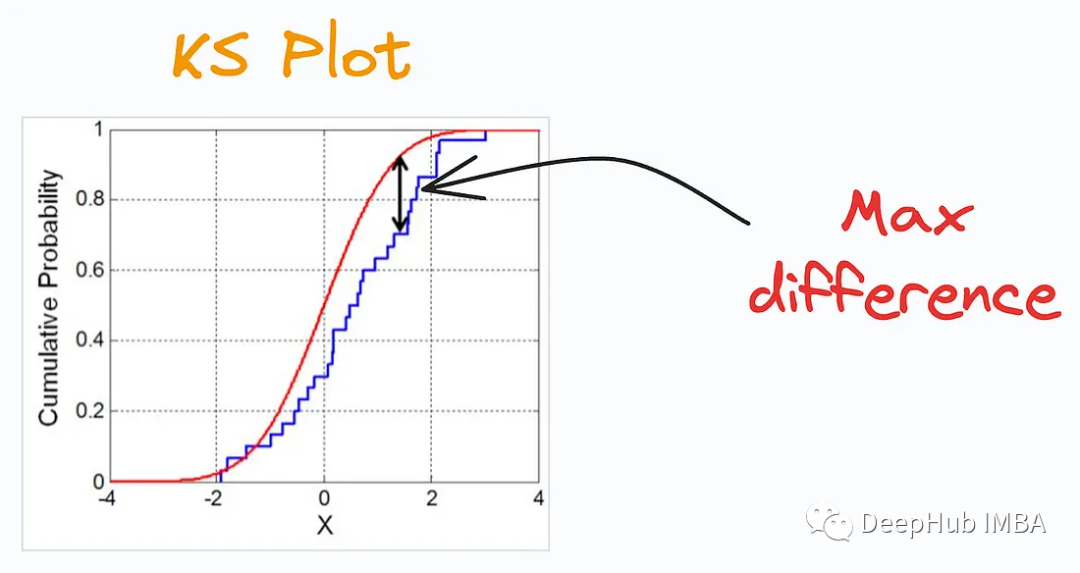
2. SHAP Plot

SHAP Plot fasst die Bedeutung von Features für die Modellvorhersage zusammen, indem es die Wechselwirkungen/Abhängigkeiten zwischen Features berücksichtigt. Nützlich, wenn Sie bestimmen möchten, wie sich unterschiedliche Werte (niedrig oder hoch) einer Funktion auf die Gesamtausgabe auswirken.

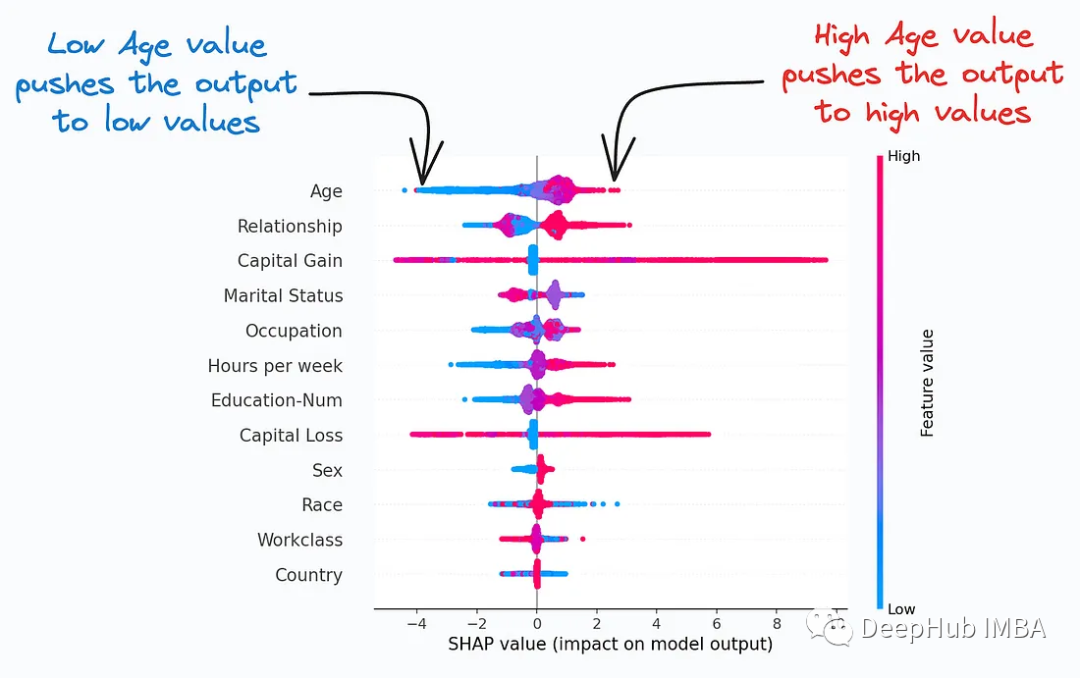
3, ROC-Kurve

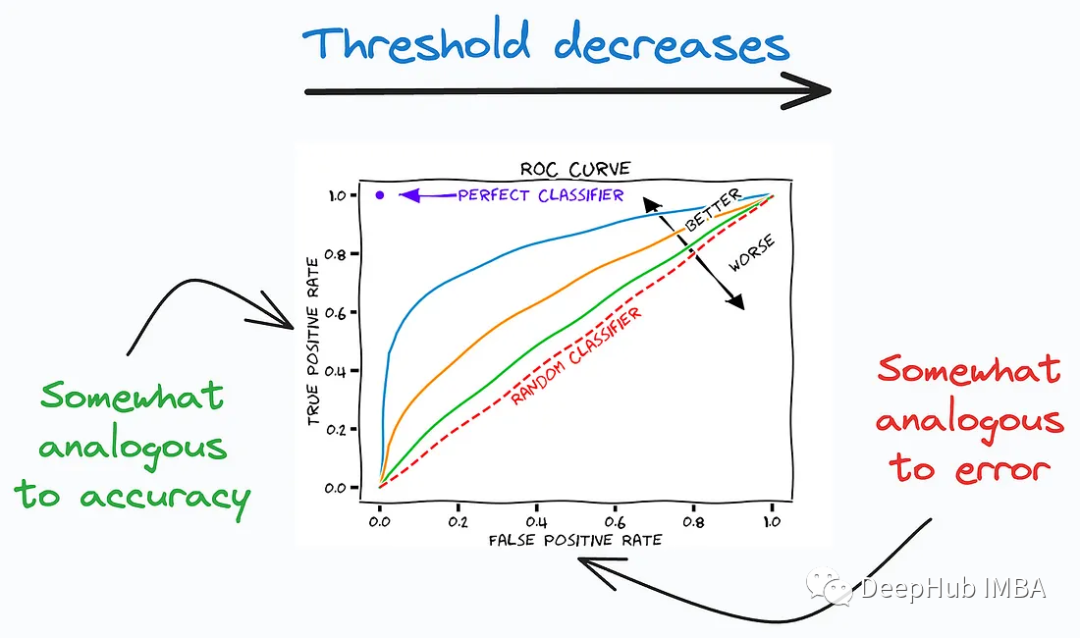
ROC-Kurve beschreibt den Kompromiss zwischen der Rate richtig positiver Ergebnisse (gute Leistung) und der Rate falsch positiver Ergebnisse (schlechte Leistung) über verschiedene Klassifizierungsschwellenwerte hinweg. Es zeigt den Kompromiss zwischen der Sensitivität (True Positive Rate, TPR) und der Spezifität (True Negative Rate, TNR) des Klassifikators bei verschiedenen Schwellenwerten.

Die ROC-Kurve ist ein häufig verwendetes Tool, das sich besonders zur Bewertung der Leistung medizinischer Diagnosetests, Klassifikatoren für maschinelles Lernen, Risikomodelle usw. eignet. Durch die Analyse von ROC-Kurven und die Berechnung von AUC können Sie die Leistung Ihres Klassifikators besser verstehen, geeignete Schwellenwerte auswählen und die Leistung verschiedener Modelle vergleichen.

4. Precision-Recall-Kurve

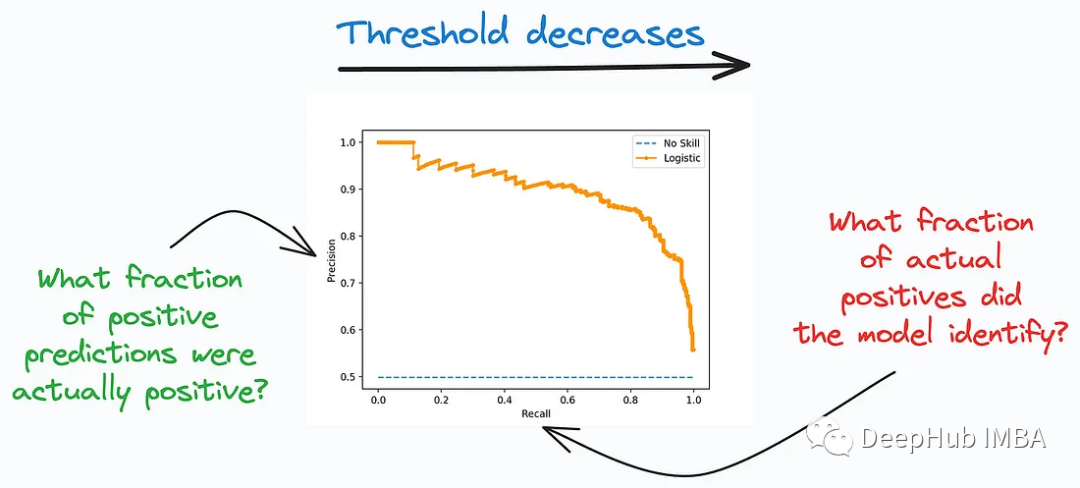
Precision-Recall-Kurve (Precision-Recall) ist ein weiteres wichtiges Werkzeug zur Bewertung der Leistung von Klassifizierungsmodellen, besonders geeignet für unausgeglichene Klassenverteilungsprobleme, bei denen die Anzahl der positive und negative Klassenstichproben sind sehr unterschiedlich. Diese Kurve konzentriert sich auf die Vorhersagegenauigkeit des Modells in der positiven Kategorie und seine Fähigkeit, alle echten positiven Beispiele zu finden. Es beschreibt den Kompromiss zwischen Präzision und Erinnerung zwischen verschiedenen Klassifizierungsschwellenwerten.

5, QQ-Diagramm

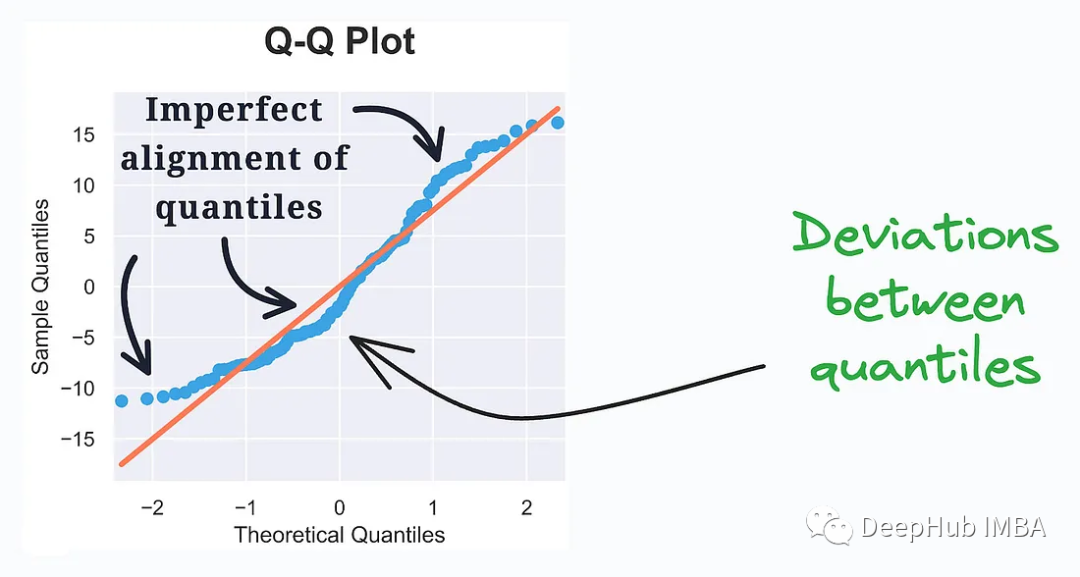
QQ-Diagramm (Quantil-Quantil-Diagramm, Quantil-Quantil-Diagramm) ist eine Methode zum Vergleichen, ob die Quantilverteilungen zweier Datensätze ähnlich sind. Es wird häufig verwendet, um zu überprüfen, ob ein Datensatz einer bestimmten theoretischen Verteilung, beispielsweise der Normalverteilung, entspricht.

Es bewertet die Verteilungsähnlichkeit zwischen den beobachteten Daten und der theoretischen Verteilung. Quantile der beiden Verteilungen werden aufgetragen. Eine Abweichung von einer Geraden stellt eine Abweichung von der angenommenen Verteilung dar.

QQ Plot ist ein intuitives Tool, mit dem die Verteilung von Daten untersucht werden kann, insbesondere bei der statistischen Modellierung und Datenanalyse. Durch Beobachtung der Position der Punkte im QQ-Plot können Sie erkennen, ob die Daten einer bestimmten theoretischen Verteilung entsprechen oder ob es Ausreißer oder Abweichungen gibt.

6. Das Diagramm der kumulativen erklärten Varianz (Cumulative Explained Variance Plot) ist ein Diagramm, das häufig bei Dimensionsreduktionstechniken wie der Hauptkomponentenanalyse (PCA) zur Erklärung von Daten verwendet wird Varianzinformationen und wählen Sie geeignete Dimensionen zur Darstellung der Daten aus.

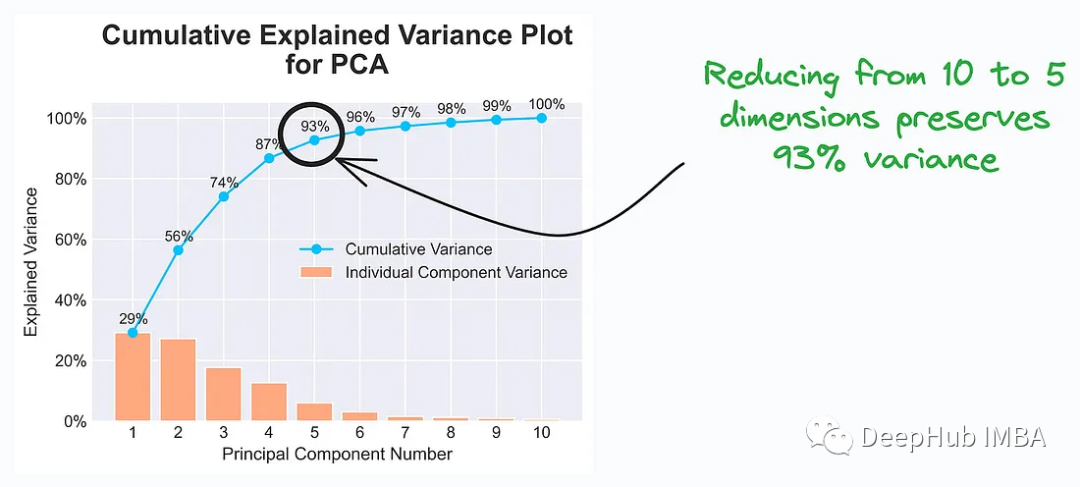Datenwissenschaftler und -analysten wählen die geeignete Anzahl von Hauptkomponenten basierend auf den Informationen im Cumulative Explained Variance Plot aus, damit die Eigenschaften der Daten nach der Dimensionsreduzierung immer noch effektiv dargestellt werden können. Dies trägt dazu bei, die Datendimensionen zu reduzieren, die Effizienz des Modelltrainings zu verbessern und genügend Informationen zu behalten, um den erfolgreichen Abschluss von Aufgaben zu unterstützen.

7. Elbow Curve

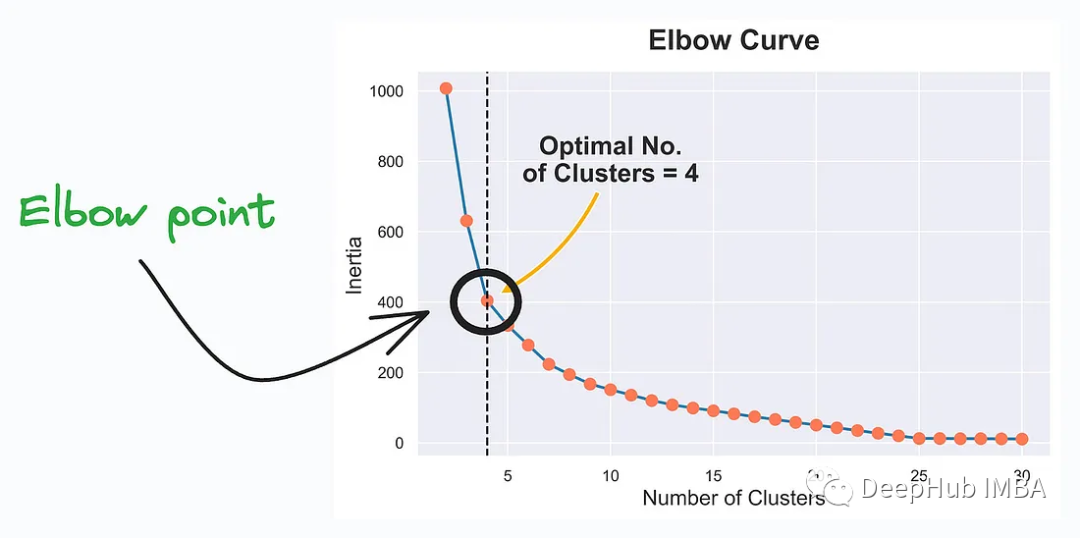
Elbow Curve ist ein Visualisierungstool, das dabei hilft, die optimale Anzahl von Clustern (Anzahl der Cluster) beim K-Means-Clustering zu bestimmen. K-Means ist ein häufig verwendeter unbeaufsichtigter Lernalgorithmus, der zur Klassifizierung von Datenpunkten in verschiedene Cluster oder Gruppen verwendet wird. Elbow Curve hilft dabei, die richtige Anzahl von Clustern zu finden, um die Struktur Ihrer Daten am besten darzustellen.

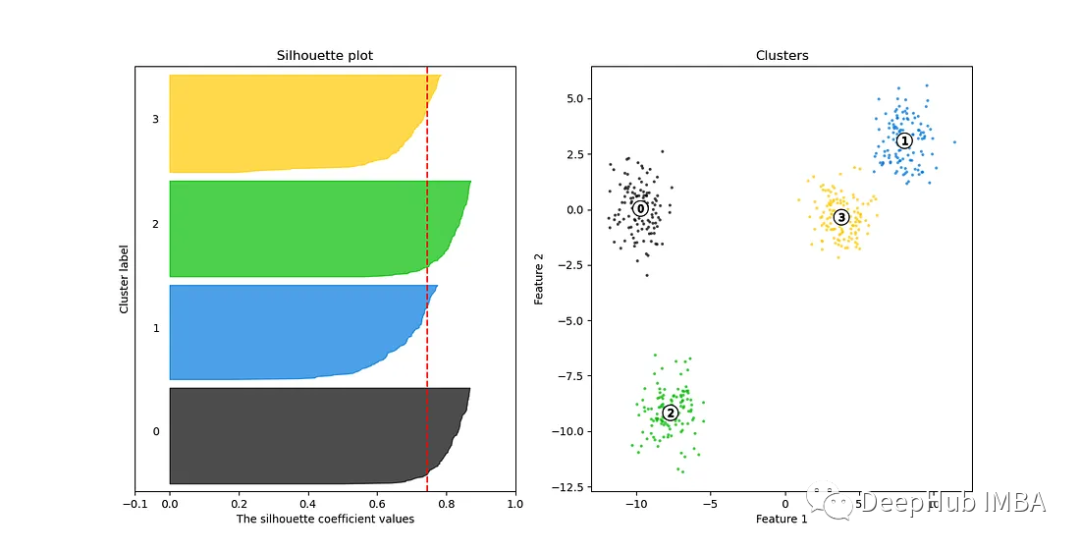
Elbow Curve ist ein häufig verwendetes Tool, um die optimale Anzahl von Clustern beim K-Means-Clustering auszuwählen. Die Punkte am Ellenbogen stellen die ideale Anzahl von Clustern dar. Dadurch werden die zugrunde liegende Struktur und Muster der Daten besser erfasst. 8, Silhouette-Kurve Der Silhouette-Koeffizient ist ein Maß für die Ähnlichkeit von Datenpunkten innerhalb von Clustern und die Trennung von Datenpunkten zwischen Clustern beim Clustering.

Silhouette Curve ist ein leistungsstarkes Tool, das dabei hilft, die optimale Anzahl von Clustern auszuwählen, um sicherzustellen, dass das Clustering-Modell die intrinsische Struktur und Muster der Daten effektiv erfassen kann. Ellenbogenkurven sind bei vielen Clustern oft wirkungslos. Silhouette Curve ist die bessere Wahl.

9, Gini-Verunreinigung und Entropie

Gini-Verunreinigung und Entropie sind zwei Indikatoren, die häufig in Algorithmen für maschinelles Lernen wie Entscheidungsbäumen und Zufallswäldern verwendet werden, um die Datenverunreinigung zu bewerten und optimale Aufteilungseigenschaften auszuwählen. Sie werden beide verwendet, um das Ausmaß der Unordnung in einem Datensatz zu messen, um Entscheidungsbäumen bei der Entscheidung zu helfen, wie die Daten aufgeteilt werden sollen.

Sie werden verwendet, um die Unreinheit oder Unordnung eines Knotens oder einer Aufteilung in einem Entscheidungsbaum zu messen. Die obige Abbildung vergleicht Gini-Verunreinigung und Entropie bei verschiedenen Aufteilungen, was Einblicke in die Kompromisse zwischen diesen Maßen geben kann.

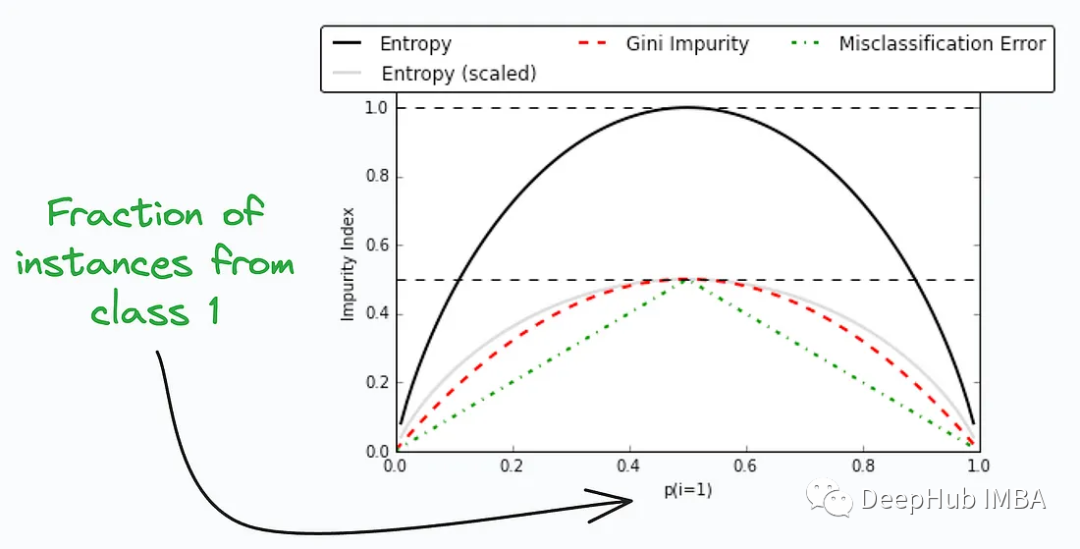Beide sind gültige Indikatoren für die Knotenaufteilungsauswahl in maschinellen Lernalgorithmen wie Entscheidungsbäumen, aber welcher man wählt, hängt vom spezifischen Problem und den Dateneigenschaften ab.

10, Bias-Varianz-Kompromiss

Der Bias-Varianz-Kompromiss (Bias-Varianz-Kompromiss) ist ein wichtiges Konzept beim maschinellen Lernen, das verwendet wird, um den Unterschied zwischen der Vorhersageleistung und der Generalisierungsfähigkeit des Modells zu erklären Gleichgewicht.

Es gibt einen Kompromiss zwischen Voreingenommenheit und Varianz. Beim Training eines maschinellen Lernmodells führt eine zunehmende Modellkomplexität normalerweise zu einer Verringerung der Verzerrung, aber zu einer Erhöhung der Varianz, während eine abnehmende Modellkomplexität zu einer Verringerung der Varianz, aber zu einer Erhöhung der Verzerrung führt. Daher gibt es einen Kompromisspunkt, bei dem das Modell sowohl in der Lage ist, Muster in den Daten zu erfassen (Verzerrung reduzieren) als auch stabile Vorhersagen über verschiedene Daten hinweg zu zeigen (Varianz reduzieren).

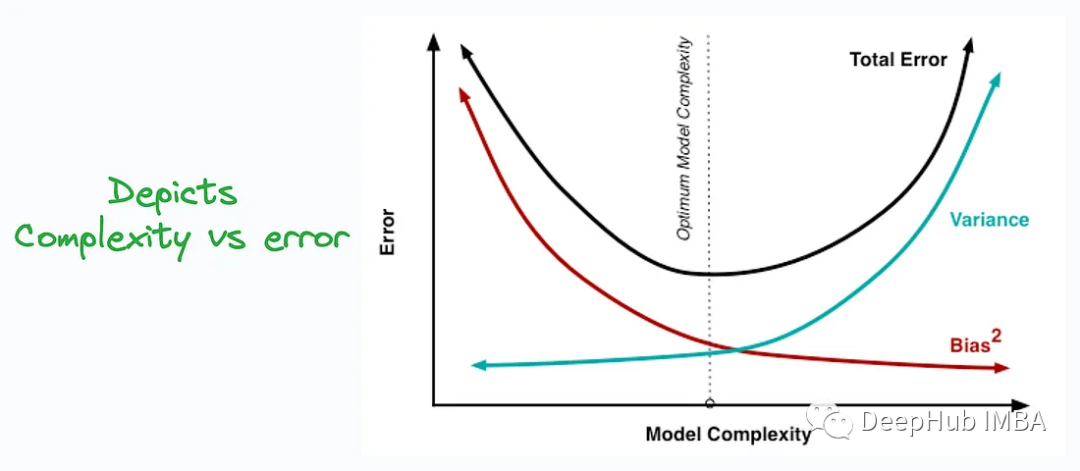Das Verständnis des Bias-Varianz-Kompromisses hilft Praktikern des maschinellen Lernens, Modelle besser zu erstellen und abzustimmen, um eine bessere Leistung und Generalisierungsfähigkeiten zu erreichen. Es beleuchtet den Zusammenhang zwischen Modellkomplexität und Datensatzgröße und zeigt, wie eine Unter- und Überanpassung vermieden werden kann.

11. Partielle Abhängigkeitsdiagramme:

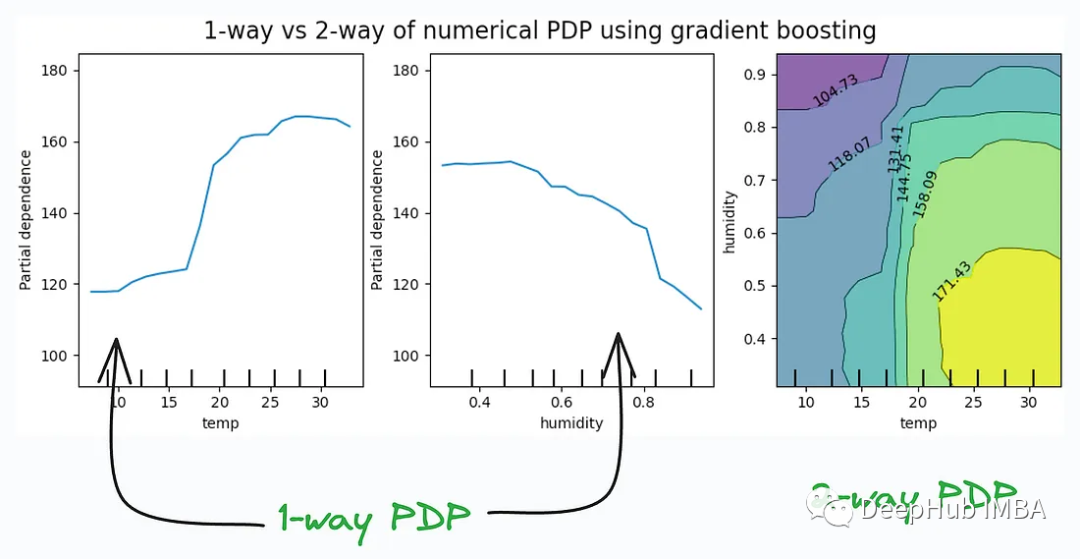
Partielle Abhängigkeitsdiagramme (Partial Dependency Plots) sind ein Werkzeug zur Visualisierung und Erklärung von Modellen für maschinelles Lernen, das besonders nützlich ist, um die Auswirkungen einzelner Funktionen auf Modellvorhersagen zu verstehen. Diese Diagramme helfen dabei, die Beziehung zwischen Merkmalen und Zielvariablen aufzuzeigen, um das Verhalten und die Entscheidungen des Modells besser zu verstehen.

Partielle Abhängigkeitsdiagramme werden häufig mit Interpretationstools und -techniken wie SHAP-Werten, LIME usw. verwendet, um die Vorhersagen von Black-Box-Modellen für maschinelles Lernen zu erklären. Sie bieten eine Visualisierung, die es Datenwissenschaftlern und Analysten erleichtert, die Beziehungen zwischen den Entscheidungen und Funktionen eines Modells zu verstehen.

Zusammenfassung

Diese Diagramme decken häufig verwendete Visualisierungstools und -konzepte in den Bereichen Datenanalyse und maschinelles Lernen ab, die dabei helfen, die Modellleistung zu bewerten und zu erklären, die Datenverteilung zu verstehen und die besten Parameter und Modelle auszuwählen. Komplexität und die Auswirkung von Insight-Funktionen auf Vorhersagen.

Das obige ist der detaillierte Inhalt von11 erweiterte Visualisierungen für Datenanalyse und maschinelles Lernen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!