Was ist Regularisierung beim maschinellen Lernen?
1. Einführung
Im Bereich des maschinellen Lernens können relevante Modelle während des Trainingsprozesses über- und unterpassen. Um dies zu verhindern, verwenden wir Regularisierungsoperationen beim maschinellen Lernen, um das Modell richtig an unseren Testsatz anzupassen. Im Allgemeinen helfen Regularisierungsoperationen jedem, das beste Modell zu erhalten, indem sie die Möglichkeit einer Über- und Unteranpassung verringern.
In diesem Artikel werden wir verstehen, was Regularisierung ist und welche Arten der Regularisierung es gibt. Darüber hinaus werden wir verwandte Konzepte wie Bias, Varianz, Unteranpassung und Überanpassung diskutieren.
Kein Unsinn mehr, fangen wir an!
2. Bias und Varianz sind zwei Aspekte, die verwendet werden, um die Lücke zwischen dem Modell, das wir gelernt haben, und dem realen Modell zu beschreiben. Was neu geschrieben werden muss, ist: die beiden Es ist wie folgt definiert:
Bias ist die Differenz zwischen dem Durchschnitt der Ausgabe aller mit allen möglichen Trainingsdatensätzen trainierten Modelle und dem Ausgabewert des realen Modells. Varianz ist die Differenz zwischen den Ausgabewerten des Modells, das auf verschiedenen Trainingsdatensätzen trainiert wurde.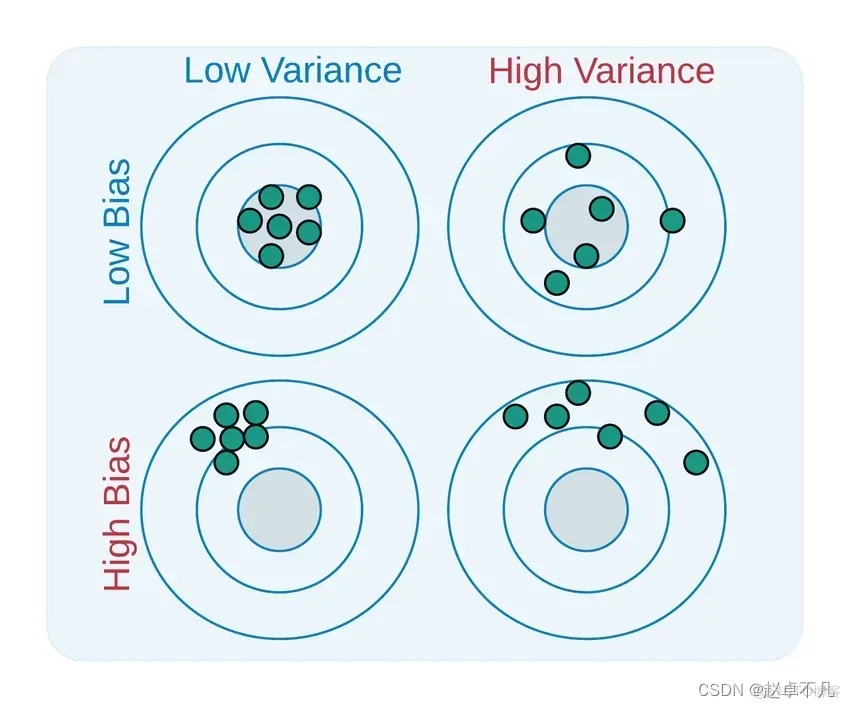 Varianz (Varianz) beim maschinellen Lernen bezieht sich auf Fehler, die durch die Empfindlichkeit des Modells gegenüber kleinen Änderungen in den Daten verursacht werden Satz. Da der Datensatz erhebliche Schwankungen aufweist, modelliert der Algorithmus Rauschen und Ausreißer im Trainingssatz. Diese Situation wird oft als Überanpassung bezeichnet. Wenn es anhand eines neuen Datensatzes ausgewertet wird, kann es keine genauen Vorhersagen liefern, da das Modell im Wesentlichen jeden Datenpunkt lernt Unteranpassung und Überanpassung.
Varianz (Varianz) beim maschinellen Lernen bezieht sich auf Fehler, die durch die Empfindlichkeit des Modells gegenüber kleinen Änderungen in den Daten verursacht werden Satz. Da der Datensatz erhebliche Schwankungen aufweist, modelliert der Algorithmus Rauschen und Ausreißer im Trainingssatz. Diese Situation wird oft als Überanpassung bezeichnet. Wenn es anhand eines neuen Datensatzes ausgewertet wird, kann es keine genauen Vorhersagen liefern, da das Modell im Wesentlichen jeden Datenpunkt lernt Unteranpassung und Überanpassung.
3. Unteranpassung
Unteranpassung tritt auf, wenn das Modell die Muster in den Trainingsdaten nicht richtig lernen und auf neue Daten verallgemeinern kann. Unterpassende Modelle schneiden bei Trainingsdaten schlecht ab und können zu falschen Vorhersagen führen. Wenn eine hohe Verzerrung und eine geringe Varianz auftreten, kann es zu einer Unteranpassung kommen Bei neuen Daten spricht man von Überanpassung. In diesem Fall wird das maschinelle Lernmodell an das Rauschen in den Trainingsdaten angepasst, was sich negativ auf die Leistung des Modells bei den Testdaten auswirkt. Ein geringer Bias und eine hohe Varianz können zu einer Überanpassung führen.
5. Regularisierungskonzept
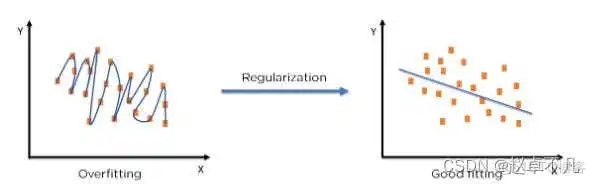
Der Begriff „Regularisierung“ beschreibt die Methode zur Kalibrierung eines maschinellen Lernmodells, um die angepasste Verlustfunktion zu reduzieren und eine Über- oder Unteranpassung zu vermeiden.
Durch den Einsatz der Regularisierungstechnologie können wir das Modell des maschinellen Lernens genauer an einen bestimmten Testsatz anpassen und so den Fehler im Testsatz effektiv reduzieren
6. L1-Regularisierung
Im Vergleich zur Collar-Regression besteht die Implementierung der L1-Regularisierung hauptsächlich darin, der Verlustfunktion einen Strafterm hinzuzufügen. Der Strafwert dieses Termes ist die Summe der absoluten Werte aller Koeffizienten wie folgt:
Im Lasso-Regressionsmodell wird dies erreicht, indem der Strafterm des Absolutwerts des Regressionskoeffizienten ähnlich wie bei der Ridge-Regression erhöht wird. Darüber hinaus bietet die L1-Regularisierung eine gute Leistung bei der Verbesserung der Genauigkeit linearer Regressionsmodelle. Da die L1-Regularisierung gleichzeitig alle Parameter gleichermaßen bestraft, kann sie gleichzeitig dazu führen, dass einige Gewichte zu Null werden, wodurch ein spärliches Modell entsteht, das bestimmte Merkmale entfernen kann (ein Gewicht von 0 entspricht einer Entfernung).
7. L2-Regularisierung
L2-Regularisierung wird auch durch Hinzufügen eines Strafterms zur Verlustfunktion erreicht, der der Summe der Quadrate aller Koeffizienten entspricht. Wie unten gezeigt:
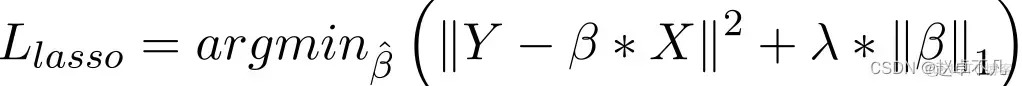
Im Allgemeinen wird dies als eine anzuwendende Methode angesehen, wenn die Daten Multikollinearität aufweisen (unabhängige Variablen sind stark korreliert). Obwohl Kleinste-Quadrate-Schätzungen (OLS) in der Multikollinearität unvoreingenommen sind, können ihre großen Varianzen dazu führen, dass beobachtete Werte erheblich von tatsächlichen Werten abweichen. L2 reduziert den Fehler von Regressionsschätzungen bis zu einem gewissen Grad. Normalerweise werden Schrumpfungsparameter verwendet, um Multikollinearitätsprobleme zu lösen. Die L2-Regularisierung reduziert den festen Anteil der Gewichte und glättet die Gewichte.
8. Zusammenfassung
Nach der obigen Analyse wird das relevante Regularisierungswissen in diesem Artikel wie folgt zusammengefasst:
L1-Regularisierung kann eine spärliche Gewichtsmatrix generieren, das heißt, ein spärliches Modell generieren , die zur Merkmalsauswahl verwendet werden kann;
L2-Regularisierung kann eine Überanpassung des Modells verhindern und die Generalisierungsfähigkeit des Modells verbessern
L1 (Lagrange)-Regularisierungshypothese Die Laplace-Verteilung kann die Sparsität des Modells sicherstellen, d des Modells, das heißt, der Wert des Parameters wird nicht zu groß oder zu klein sein
Wenn das Merkmal in der Praxis hochdimensional und dünn besetzt ist, sollte die L1-Regularisierung verwendet werden, wenn das Merkmal niedrigdimensional und dicht ist , L2-Regularisierung sollte verwendet werden
Das obige ist der detaillierte Inhalt vonWas ist Regularisierung beim maschinellen Lernen?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 15 empfohlene kostenlose Open-Source-Bildanmerkungstools
Mar 28, 2024 pm 01:21 PM
15 empfohlene kostenlose Open-Source-Bildanmerkungstools
Mar 28, 2024 pm 01:21 PM
Bei der Bildanmerkung handelt es sich um das Verknüpfen von Beschriftungen oder beschreibenden Informationen mit Bildern, um dem Bildinhalt eine tiefere Bedeutung und Erklärung zu verleihen. Dieser Prozess ist entscheidend für maschinelles Lernen, das dabei hilft, Sehmodelle zu trainieren, um einzelne Elemente in Bildern genauer zu identifizieren. Durch das Hinzufügen von Anmerkungen zu Bildern kann der Computer die Semantik und den Kontext hinter den Bildern verstehen und so den Bildinhalt besser verstehen und analysieren. Die Bildanmerkung hat ein breites Anwendungsspektrum und deckt viele Bereiche ab, z. B. Computer Vision, Verarbeitung natürlicher Sprache und Diagramm-Vision-Modelle. Sie verfügt über ein breites Anwendungsspektrum, z. B. zur Unterstützung von Fahrzeugen bei der Identifizierung von Hindernissen auf der Straße und bei der Erkennung und Diagnose von Krankheiten durch medizinische Bilderkennung. In diesem Artikel werden hauptsächlich einige bessere Open-Source- und kostenlose Bildanmerkungstools empfohlen. 1.Makesens
 In diesem Artikel erfahren Sie mehr über SHAP: Modellerklärung für maschinelles Lernen
Jun 01, 2024 am 10:58 AM
In diesem Artikel erfahren Sie mehr über SHAP: Modellerklärung für maschinelles Lernen
Jun 01, 2024 am 10:58 AM
In den Bereichen maschinelles Lernen und Datenwissenschaft stand die Interpretierbarkeit von Modellen schon immer im Fokus von Forschern und Praktikern. Mit der weit verbreiteten Anwendung komplexer Modelle wie Deep Learning und Ensemble-Methoden ist das Verständnis des Entscheidungsprozesses des Modells besonders wichtig geworden. Explainable AI|XAI trägt dazu bei, Vertrauen in maschinelle Lernmodelle aufzubauen, indem es die Transparenz des Modells erhöht. Eine Verbesserung der Modelltransparenz kann durch Methoden wie den weit verbreiteten Einsatz mehrerer komplexer Modelle sowie der Entscheidungsprozesse zur Erläuterung der Modelle erreicht werden. Zu diesen Methoden gehören die Analyse der Merkmalsbedeutung, die Schätzung des Modellvorhersageintervalls, lokale Interpretierbarkeitsalgorithmen usw. Die Merkmalswichtigkeitsanalyse kann den Entscheidungsprozess des Modells erklären, indem sie den Grad des Einflusses des Modells auf die Eingabemerkmale bewertet. Schätzung des Modellvorhersageintervalls
 Transparent! Eine ausführliche Analyse der Prinzipien der wichtigsten Modelle des maschinellen Lernens!
Apr 12, 2024 pm 05:55 PM
Transparent! Eine ausführliche Analyse der Prinzipien der wichtigsten Modelle des maschinellen Lernens!
Apr 12, 2024 pm 05:55 PM
Laienhaft ausgedrückt ist ein Modell für maschinelles Lernen eine mathematische Funktion, die Eingabedaten einer vorhergesagten Ausgabe zuordnet. Genauer gesagt ist ein Modell für maschinelles Lernen eine mathematische Funktion, die Modellparameter anpasst, indem sie aus Trainingsdaten lernt, um den Fehler zwischen der vorhergesagten Ausgabe und der wahren Bezeichnung zu minimieren. Beim maschinellen Lernen gibt es viele Modelle, z. B. logistische Regressionsmodelle, Entscheidungsbaummodelle, Support-Vektor-Maschinenmodelle usw. Jedes Modell verfügt über seine anwendbaren Datentypen und Problemtypen. Gleichzeitig gibt es viele Gemeinsamkeiten zwischen verschiedenen Modellen oder es gibt einen verborgenen Weg für die Modellentwicklung. Am Beispiel des konnektionistischen Perzeptrons können wir es durch Erhöhen der Anzahl verborgener Schichten des Perzeptrons in ein tiefes neuronales Netzwerk umwandeln. Wenn dem Perzeptron eine Kernelfunktion hinzugefügt wird, kann es in eine SVM umgewandelt werden. Dieses hier
 Identifizieren Sie Über- und Unteranpassung anhand von Lernkurven
Apr 29, 2024 pm 06:50 PM
Identifizieren Sie Über- und Unteranpassung anhand von Lernkurven
Apr 29, 2024 pm 06:50 PM
In diesem Artikel wird vorgestellt, wie Überanpassung und Unteranpassung in Modellen für maschinelles Lernen mithilfe von Lernkurven effektiv identifiziert werden können. Unteranpassung und Überanpassung 1. Überanpassung Wenn ein Modell mit den Daten übertrainiert ist, sodass es daraus Rauschen lernt, spricht man von einer Überanpassung des Modells. Ein überangepasstes Modell lernt jedes Beispiel so perfekt, dass es ein unsichtbares/neues Beispiel falsch klassifiziert. Für ein überangepasstes Modell erhalten wir einen perfekten/nahezu perfekten Trainingssatzwert und einen schrecklichen Validierungssatz-/Testwert. Leicht geändert: „Ursache der Überanpassung: Verwenden Sie ein komplexes Modell, um ein einfaches Problem zu lösen und Rauschen aus den Daten zu extrahieren. Weil ein kleiner Datensatz als Trainingssatz möglicherweise nicht die korrekte Darstellung aller Daten darstellt. 2. Unteranpassung Heru.“
 Die Entwicklung der künstlichen Intelligenz in der Weltraumforschung und der Siedlungstechnik
Apr 29, 2024 pm 03:25 PM
Die Entwicklung der künstlichen Intelligenz in der Weltraumforschung und der Siedlungstechnik
Apr 29, 2024 pm 03:25 PM
In den 1950er Jahren wurde die künstliche Intelligenz (KI) geboren. Damals entdeckten Forscher, dass Maschinen menschenähnliche Aufgaben wie das Denken ausführen können. Später, in den 1960er Jahren, finanzierte das US-Verteidigungsministerium künstliche Intelligenz und richtete Labore für die weitere Entwicklung ein. Forscher finden Anwendungen für künstliche Intelligenz in vielen Bereichen, etwa bei der Erforschung des Weltraums und beim Überleben in extremen Umgebungen. Unter Weltraumforschung versteht man die Erforschung des Universums, das das gesamte Universum außerhalb der Erde umfasst. Der Weltraum wird als extreme Umgebung eingestuft, da sich seine Bedingungen von denen auf der Erde unterscheiden. Um im Weltraum zu überleben, müssen viele Faktoren berücksichtigt und Vorkehrungen getroffen werden. Wissenschaftler und Forscher glauben, dass die Erforschung des Weltraums und das Verständnis des aktuellen Zustands aller Dinge dazu beitragen können, die Funktionsweise des Universums zu verstehen und sich auf mögliche Umweltkrisen vorzubereiten
 Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Zu den häufigsten Herausforderungen, mit denen Algorithmen für maschinelles Lernen in C++ konfrontiert sind, gehören Speicherverwaltung, Multithreading, Leistungsoptimierung und Wartbarkeit. Zu den Lösungen gehören die Verwendung intelligenter Zeiger, moderner Threading-Bibliotheken, SIMD-Anweisungen und Bibliotheken von Drittanbietern sowie die Einhaltung von Codierungsstilrichtlinien und die Verwendung von Automatisierungstools. Praktische Fälle zeigen, wie man die Eigen-Bibliothek nutzt, um lineare Regressionsalgorithmen zu implementieren, den Speicher effektiv zu verwalten und leistungsstarke Matrixoperationen zu nutzen.
 Erklärbare KI: Erklären komplexer KI/ML-Modelle
Jun 03, 2024 pm 10:08 PM
Erklärbare KI: Erklären komplexer KI/ML-Modelle
Jun 03, 2024 pm 10:08 PM
Übersetzer |. Rezensiert von Li Rui |. Chonglou Modelle für künstliche Intelligenz (KI) und maschinelles Lernen (ML) werden heutzutage immer komplexer, und die von diesen Modellen erzeugten Ergebnisse sind eine Blackbox, die den Stakeholdern nicht erklärt werden kann. Explainable AI (XAI) zielt darauf ab, dieses Problem zu lösen, indem es Stakeholdern ermöglicht, die Funktionsweise dieser Modelle zu verstehen, sicherzustellen, dass sie verstehen, wie diese Modelle tatsächlich Entscheidungen treffen, und Transparenz in KI-Systemen, Vertrauen und Verantwortlichkeit zur Lösung dieses Problems gewährleistet. In diesem Artikel werden verschiedene Techniken der erklärbaren künstlichen Intelligenz (XAI) untersucht, um ihre zugrunde liegenden Prinzipien zu veranschaulichen. Mehrere Gründe, warum erklärbare KI von entscheidender Bedeutung ist. Vertrauen und Transparenz: Damit KI-Systeme allgemein akzeptiert und vertrauenswürdig sind, müssen Benutzer verstehen, wie Entscheidungen getroffen werden
 Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Maschinelles Lernen ist ein wichtiger Zweig der künstlichen Intelligenz, der Computern die Möglichkeit gibt, aus Daten zu lernen und ihre Fähigkeiten zu verbessern, ohne explizit programmiert zu werden. Maschinelles Lernen hat ein breites Anwendungsspektrum in verschiedenen Bereichen, von der Bilderkennung und der Verarbeitung natürlicher Sprache bis hin zu Empfehlungssystemen und Betrugserkennung, und es verändert unsere Lebensweise. Im Bereich des maschinellen Lernens gibt es viele verschiedene Methoden und Theorien, von denen die fünf einflussreichsten Methoden als „Fünf Schulen des maschinellen Lernens“ bezeichnet werden. Die fünf Hauptschulen sind die symbolische Schule, die konnektionistische Schule, die evolutionäre Schule, die Bayes'sche Schule und die Analogieschule. 1. Der Symbolismus, auch Symbolismus genannt, betont die Verwendung von Symbolen zum logischen Denken und zum Ausdruck von Wissen. Diese Denkrichtung glaubt, dass Lernen ein Prozess der umgekehrten Schlussfolgerung durch das Vorhandene ist




