Technologie-Peripheriegeräte
KI
11 grundlegende Methoden zur Bestimmung der Normalität von Datenverteilungen
11 grundlegende Methoden zur Bestimmung der Normalität von Datenverteilungen
Im Bereich der Datenwissenschaft und des maschinellen Lernens gehen viele Modelle davon aus, dass die Daten normalverteilt sind oder dass die Daten bei einer Normalverteilung besser abschneiden. Beispielsweise geht die lineare Regression davon aus, dass die Residuen normalverteilt sind, und die lineare Diskriminanzanalyse (LDA) wird auf der Grundlage von Annahmen wie der Normalverteilung abgeleitet. Daher ist es für Datenwissenschaftler und Praktiker des maschinellen Lernens von entscheidender Bedeutung zu verstehen, wie die Normalität von Daten getestet werden kann wie man geeignete Analysemethoden anwendet. Dies kann die Auswirkungen der Datenverteilung auf die Modellleistung besser bewältigen und den Prozess des maschinellen Lernens und der Datenmodellierung komfortabler gestalten Die Verteilung entspricht einer Normalverteilung. Im QQ-Diagramm werden die Quantile der Daten mit den Quantilen der Standardnormalverteilung verglichen. Wenn die Datenverteilung nahe an der Normalverteilung liegt, liegen die Punkte im QQ-Diagramm nahe an einer geraden Linie QQ-Diagramm: Der Beispielcode generiert einen Satz Zufallsdaten, die einer Normalverteilung folgen. Nachdem Sie den Code ausgeführt haben, können Sie das QQ-Diagramm zusammen mit der entsprechenden Normalverteilungskurve sehen. Indem Sie die Verteilung der Punkte im Diagramm beobachten, können Sie zunächst beurteilen, ob die Daten einer Normalverteilung nahe kommen.
3. Violin-Diagramm
Sie können die Verteilung der Daten ermitteln durch Beobachtung der Violin-Plot-Form, um zunächst festzustellen, ob die Daten einer Normalverteilung nahe kommen. Wenn der Violin Plot eine glockenkurvenartige Form annimmt, sind die Daten wahrscheinlich annähernd normalverteilt. Wenn Ihr Violin-Plot stark verzerrt ist oder mehrere Spitzen aufweist, sind die Daten möglicherweise nicht normalverteilt.
Der folgende Beispielcode wird verwendet, um Zufallsdaten nach einer Normalverteilung zu generieren, um Violin Plot zu demonstrieren. Nachdem Sie den Code ausgeführt haben, können Sie das Violindiagramm und die entsprechende Normalverteilungskurve sehen. Erkennen Sie die Form der Datenverteilung durch Visualisierung, um zunächst zu beurteilen, ob die Daten einer Normalverteilung nahe kommen Methode. Histogramme können uns helfen, die Verteilung von Daten intuitiv zu verstehen, und können vorab feststellen, ob die Daten einer Normalverteilung nahe kommen mit der entsprechenden Normalverteilung. Wenn die Kurvenformen ähnlich sind, sind die Daten wahrscheinlich normalverteilt. Natürlich ist die Visualisierung nur eine vorläufige Beurteilung. Wenn eine genauere Erkennung erforderlich ist, können statistische Methoden wie Normalitätstests zur Analyse verwendet werden.
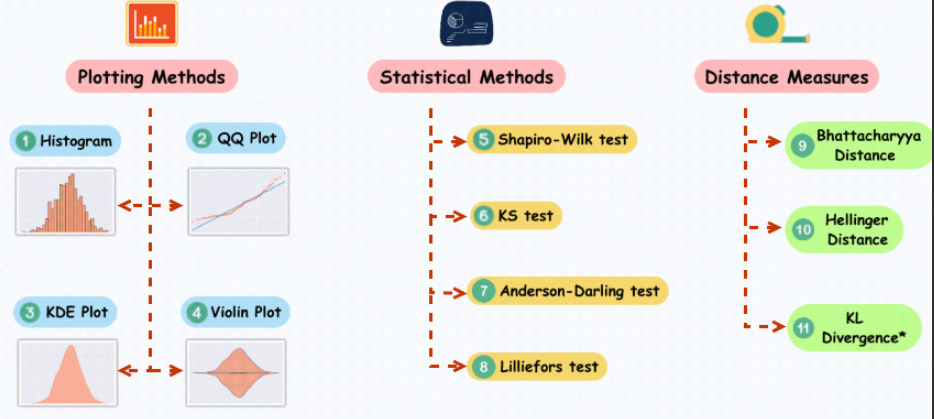
Statistische Methoden
5. Shapiro-Wilk-Test
Der Shapiro-Wilk-Test ist eine statistische Methode zum Testen, ob die Daten der Normalverteilung entsprechen, auch bekannt als W-Test. Bei der Durchführung des Shapiro-Wilk-Tests konzentrieren wir uns normalerweise auf zwei Hauptindikatoren: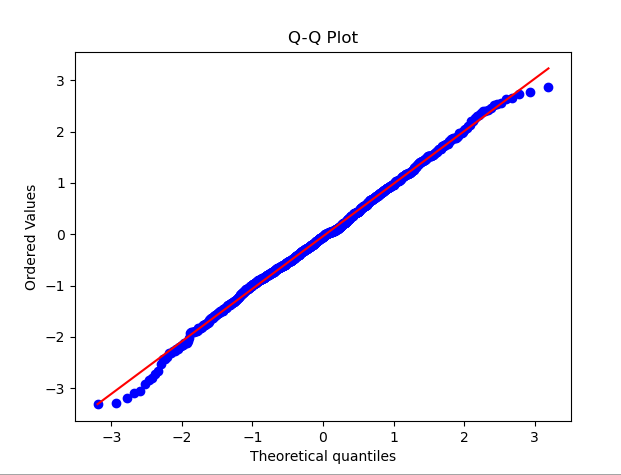 
Statistik W: Berechnen Sie die Statistik W basierend auf der Korrelation zwischen den beobachteten Daten und dem erwarteten Wert unter der Normalverteilung und dem Wertebereich von W Dazwischen 0 und 1, wenn W nahe bei 1 liegt, bedeutet dies, dass die beobachteten Daten besser zur Normalverteilung passen.
P-Wert: Der P-Wert gibt die Wahrscheinlichkeit der Beobachtung dieser Korrelation an. Wenn der P-Wert größer als das Signifikanzniveau (normalerweise 0,05) ist, deutet dies darauf hin, dass die beobachteten Daten wahrscheinlich aus einer Normalverteilung stammen.
Wenn die Statistik W nahe bei 1 liegt und der P-Wert größer als 0,05 ist, können wir daraus schließen, dass die beobachteten Daten die Normalverteilung erfüllen.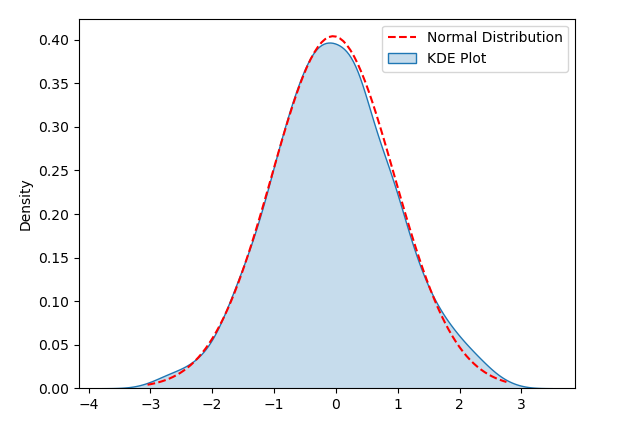
Im folgenden Code wird zunächst ein Satz zufälliger Daten generiert, die der Normalverteilung entsprechen, und dann wird der Shapiro-Wilk-Test durchgeführt, um die Teststatistik und den P-Wert zu erhalten. Anhand des Vergleichs zwischen dem P-Wert und dem Signifikanzniveau können Sie feststellen, ob die Stichprobendaten aus einer Normalverteilung stammen.
from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Shapiro-Wilk检验stat, p = stats.shapiro(data)print('Shapiro-Wilk Statistic:', stat)print('P-value:', p)# 根据P值判断正态性alpha = 0.05if p > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')
6.KS检验
KS检验（Kolmogorov-Smirnov检验）是一种用于检验数据是否符合特定分布（例如正态分布）的统计方法。它通过计算观测数据与理论分布的累积分布函数（CDF）之间的最大差异来评估它们是否来自同一分布。其基本步骤如下：
- 对两个样本数据进行排序。
- 计算两个样本的经验累积分布函数(ECDF)，即计算每个值在样本中的累积百分比。
- 计算两个累积分布函数之间的差异，通常使用KS统计量衡量。
- 根据样本的大小和显著性水平，使用参考表活计算p值判断两个样本是否来自同一分布。
Python中使用KS检验来检验数据是否符合正态分布时，可以使用Scipy库中的kstest函数。下面是一个简单的示例，演示了如何使用Python进行KS检验来检验数据是否符合正态分布。
from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行KS检验statistic, p_value = stats.kstest(data, 'norm')print('KS Statistic:', statistic)print('P-value:', p_value)# 根据P值判断正态性alpha = 0.05if p_value > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')
7.Anderson-Darling检验
Anderson-Darling检验是一种用于检验数据是否来自特定分布（例如正态分布）的统计方法。它特别强调观察值在分布尾部的差异，因此在检测极端值的偏差方面非常有效
下面的代码使用stats.anderson函数执行Anderson-Darling检验，并获取检验统计量、临界值以及显著性水平。然后通过比较统计量和临界值，可以判断样本数据是否符合正态分布
from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Anderson-Darling检验result = stats.anderson(data, dist='norm')print('Anderson-Darling Statistic:', result.statistic)print('Critical Values:', result.critical_values)print('Significance Level:', result.significance_level)# 判断正态性if result.statistic <p style="text-align:center;"><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/article/000/887/227/170255826239547.png" class="lazy" alt="11 grundlegende Methoden zur Bestimmung der Normalität von Datenverteilungen"></p><h4 id="Lilliefors检验">8.Lilliefors检验</h4><p>Lilliefors检验（也被称为Kolmogorov-Smirnov-Lilliefors检验）是一种用于检验数据是否符合正态分布的统计检验方法。它是Kolmogorov-Smirnov检验的一种变体，专门用于小样本情况。与K-S检验不同，Lilliefors检验不需要假定数据的分布类型，而是基于观测数据来评估是否符合正态分布</p><p>在下面的例子中，我们使用lilliefors函数进行Lilliefors检验，并获得了检验统计量和P值。通过将P值与显著性水平进行比较，我们可以判断样本数据是否符合正态分布</p><pre class="brush:php;toolbar:false">import numpy as npfrom statsmodels.stats.diagnostic import lilliefors# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Lilliefors检验statistic, p_value = lilliefors(data)print('Lilliefors Statistic:', statistic)print('P-value:', p_value)# 根据P值判断正态性alpha = 0.05if p_value > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')
9.距离测量Distance Measures
距离测量（Distance measures）是一种有效的测试数据正态性的方法，它提供了更直观的方式来比较观察数据分布与参考分布之间的差异。
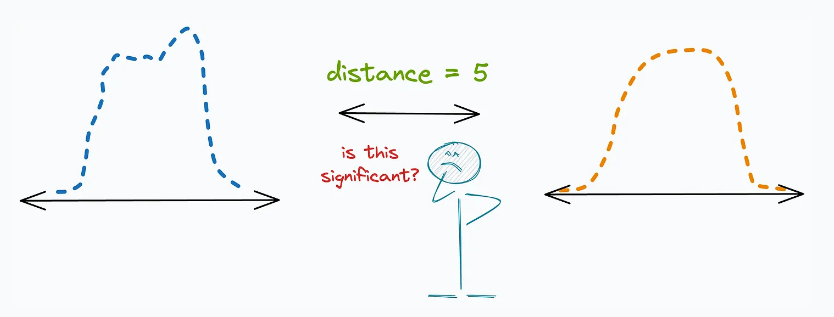
下面是一些常见的距离测量方法及其在测试正态性时的应用：
(1) "巴氏距离（Bhattacharyya distance）"的定义是：
- 测量两个分布之间的重叠，通常被解释为两个分布之间的接近程度。
- 选择与观察到的分布具有最小Bhattacharyya距离的参考分布，作为最接近的分布。
(2) 「海林格距离（Hellinger distance）」：
- 用于衡量两个分布之间的相似度，类似于Bhattacharyya距离。
- 与Bhattacharyya距离不同的是，Hellinger距离满足三角不等式，这使得它在一些情况下更为实用。
(3) "KL 散度（KL Divergence）"：
- 它本身并不是严格意义上的“距离度量”，但在测试正态性时可以用作衡量信息丢失的指标。
- 选择与观察到的分布具有最小KL散度的参考分布，作为最接近的分布。
运用这些距离测量方法，我们能够比对观测到的分布与多个参考分布之间的差异，进而更好地评估数据的正态性。通过找出与观察到的分布距离最短的参考分布，我们可以更精确地判断数据是否符合正态分布
Das obige ist der detaillierte Inhalt von11 grundlegende Methoden zur Bestimmung der Normalität von Datenverteilungen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
Heiße KI -Werkzeuge
Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos
AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.
Undress AI Tool
Ausziehbilder kostenlos
Clothoff.io
KI-Kleiderentferner
AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.
Heißer Artikel
Heiße Werkzeuge
Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor
SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen
Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung
Dreamweaver CS6
Visuelle Webentwicklungstools
SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)
Heiße Themen
1359
52
In diesem Artikel erfahren Sie mehr über SHAP: Modellerklärung für maschinelles Lernen
Jun 01, 2024 am 10:58 AM
In den Bereichen maschinelles Lernen und Datenwissenschaft stand die Interpretierbarkeit von Modellen schon immer im Fokus von Forschern und Praktikern. Mit der weit verbreiteten Anwendung komplexer Modelle wie Deep Learning und Ensemble-Methoden ist das Verständnis des Entscheidungsprozesses des Modells besonders wichtig geworden. Explainable AI|XAI trägt dazu bei, Vertrauen in maschinelle Lernmodelle aufzubauen, indem es die Transparenz des Modells erhöht. Eine Verbesserung der Modelltransparenz kann durch Methoden wie den weit verbreiteten Einsatz mehrerer komplexer Modelle sowie der Entscheidungsprozesse zur Erläuterung der Modelle erreicht werden. Zu diesen Methoden gehören die Analyse der Merkmalsbedeutung, die Schätzung des Modellvorhersageintervalls, lokale Interpretierbarkeitsalgorithmen usw. Die Merkmalswichtigkeitsanalyse kann den Entscheidungsprozess des Modells erklären, indem sie den Grad des Einflusses des Modells auf die Eingabemerkmale bewertet. Schätzung des Modellvorhersageintervalls
Transparent! Eine ausführliche Analyse der Prinzipien der wichtigsten Modelle des maschinellen Lernens!
Apr 12, 2024 pm 05:55 PM
Laienhaft ausgedrückt ist ein Modell für maschinelles Lernen eine mathematische Funktion, die Eingabedaten einer vorhergesagten Ausgabe zuordnet. Genauer gesagt ist ein Modell für maschinelles Lernen eine mathematische Funktion, die Modellparameter anpasst, indem sie aus Trainingsdaten lernt, um den Fehler zwischen der vorhergesagten Ausgabe und der wahren Bezeichnung zu minimieren. Beim maschinellen Lernen gibt es viele Modelle, z. B. logistische Regressionsmodelle, Entscheidungsbaummodelle, Support-Vektor-Maschinenmodelle usw. Jedes Modell verfügt über seine anwendbaren Datentypen und Problemtypen. Gleichzeitig gibt es viele Gemeinsamkeiten zwischen verschiedenen Modellen oder es gibt einen verborgenen Weg für die Modellentwicklung. Am Beispiel des konnektionistischen Perzeptrons können wir es durch Erhöhen der Anzahl verborgener Schichten des Perzeptrons in ein tiefes neuronales Netzwerk umwandeln. Wenn dem Perzeptron eine Kernelfunktion hinzugefügt wird, kann es in eine SVM umgewandelt werden. Dieses hier
Identifizieren Sie Über- und Unteranpassung anhand von Lernkurven
Apr 29, 2024 pm 06:50 PM
In diesem Artikel wird vorgestellt, wie Überanpassung und Unteranpassung in Modellen für maschinelles Lernen mithilfe von Lernkurven effektiv identifiziert werden können. Unteranpassung und Überanpassung 1. Überanpassung Wenn ein Modell mit den Daten übertrainiert ist, sodass es daraus Rauschen lernt, spricht man von einer Überanpassung des Modells. Ein überangepasstes Modell lernt jedes Beispiel so perfekt, dass es ein unsichtbares/neues Beispiel falsch klassifiziert. Für ein überangepasstes Modell erhalten wir einen perfekten/nahezu perfekten Trainingssatzwert und einen schrecklichen Validierungssatz-/Testwert. Leicht geändert: „Ursache der Überanpassung: Verwenden Sie ein komplexes Modell, um ein einfaches Problem zu lösen und Rauschen aus den Daten zu extrahieren. Weil ein kleiner Datensatz als Trainingssatz möglicherweise nicht die korrekte Darstellung aller Daten darstellt. 2. Unteranpassung Heru.“
Die Entwicklung der künstlichen Intelligenz in der Weltraumforschung und der Siedlungstechnik
Apr 29, 2024 pm 03:25 PM
In den 1950er Jahren wurde die künstliche Intelligenz (KI) geboren. Damals entdeckten Forscher, dass Maschinen menschenähnliche Aufgaben wie das Denken ausführen können. Später, in den 1960er Jahren, finanzierte das US-Verteidigungsministerium künstliche Intelligenz und richtete Labore für die weitere Entwicklung ein. Forscher finden Anwendungen für künstliche Intelligenz in vielen Bereichen, etwa bei der Erforschung des Weltraums und beim Überleben in extremen Umgebungen. Unter Weltraumforschung versteht man die Erforschung des Universums, das das gesamte Universum außerhalb der Erde umfasst. Der Weltraum wird als extreme Umgebung eingestuft, da sich seine Bedingungen von denen auf der Erde unterscheiden. Um im Weltraum zu überleben, müssen viele Faktoren berücksichtigt und Vorkehrungen getroffen werden. Wissenschaftler und Forscher glauben, dass die Erforschung des Weltraums und das Verständnis des aktuellen Zustands aller Dinge dazu beitragen können, die Funktionsweise des Universums zu verstehen und sich auf mögliche Umweltkrisen vorzubereiten
Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Zu den häufigsten Herausforderungen, mit denen Algorithmen für maschinelles Lernen in C++ konfrontiert sind, gehören Speicherverwaltung, Multithreading, Leistungsoptimierung und Wartbarkeit. Zu den Lösungen gehören die Verwendung intelligenter Zeiger, moderner Threading-Bibliotheken, SIMD-Anweisungen und Bibliotheken von Drittanbietern sowie die Einhaltung von Codierungsstilrichtlinien und die Verwendung von Automatisierungstools. Praktische Fälle zeigen, wie man die Eigen-Bibliothek nutzt, um lineare Regressionsalgorithmen zu implementieren, den Speicher effektiv zu verwalten und leistungsstarke Matrixoperationen zu nutzen.
Erklärbare KI: Erklären komplexer KI/ML-Modelle
Jun 03, 2024 pm 10:08 PM
Übersetzer |. Rezensiert von Li Rui |. Chonglou Modelle für künstliche Intelligenz (KI) und maschinelles Lernen (ML) werden heutzutage immer komplexer, und die von diesen Modellen erzeugten Ergebnisse sind eine Blackbox, die den Stakeholdern nicht erklärt werden kann. Explainable AI (XAI) zielt darauf ab, dieses Problem zu lösen, indem es Stakeholdern ermöglicht, die Funktionsweise dieser Modelle zu verstehen, sicherzustellen, dass sie verstehen, wie diese Modelle tatsächlich Entscheidungen treffen, und Transparenz in KI-Systemen, Vertrauen und Verantwortlichkeit zur Lösung dieses Problems gewährleistet. In diesem Artikel werden verschiedene Techniken der erklärbaren künstlichen Intelligenz (XAI) untersucht, um ihre zugrunde liegenden Prinzipien zu veranschaulichen. Mehrere Gründe, warum erklärbare KI von entscheidender Bedeutung ist. Vertrauen und Transparenz: Damit KI-Systeme allgemein akzeptiert und vertrauenswürdig sind, müssen Benutzer verstehen, wie Entscheidungen getroffen werden
Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Maschinelles Lernen ist ein wichtiger Zweig der künstlichen Intelligenz, der Computern die Möglichkeit gibt, aus Daten zu lernen und ihre Fähigkeiten zu verbessern, ohne explizit programmiert zu werden. Maschinelles Lernen hat ein breites Anwendungsspektrum in verschiedenen Bereichen, von der Bilderkennung und der Verarbeitung natürlicher Sprache bis hin zu Empfehlungssystemen und Betrugserkennung, und es verändert unsere Lebensweise. Im Bereich des maschinellen Lernens gibt es viele verschiedene Methoden und Theorien, von denen die fünf einflussreichsten Methoden als „Fünf Schulen des maschinellen Lernens“ bezeichnet werden. Die fünf Hauptschulen sind die symbolische Schule, die konnektionistische Schule, die evolutionäre Schule, die Bayes'sche Schule und die Analogieschule. 1. Der Symbolismus, auch Symbolismus genannt, betont die Verwendung von Symbolen zum logischen Denken und zum Ausdruck von Wissen. Diese Denkrichtung glaubt, dass Lernen ein Prozess der umgekehrten Schlussfolgerung durch das Vorhandene ist
Ist Flash Attention stabil? Meta und Harvard stellten fest, dass die Gewichtsabweichungen ihrer Modelle um Größenordnungen schwankten
May 30, 2024 pm 01:24 PM
MetaFAIR hat sich mit Harvard zusammengetan, um einen neuen Forschungsrahmen zur Optimierung der Datenverzerrung bereitzustellen, die bei der Durchführung groß angelegten maschinellen Lernens entsteht. Es ist bekannt, dass das Training großer Sprachmodelle oft Monate dauert und Hunderte oder sogar Tausende von GPUs verwendet. Am Beispiel des Modells LLaMA270B erfordert das Training insgesamt 1.720.320 GPU-Stunden. Das Training großer Modelle stellt aufgrund des Umfangs und der Komplexität dieser Arbeitsbelastungen einzigartige systemische Herausforderungen dar. In letzter Zeit haben viele Institutionen über Instabilität im Trainingsprozess beim Training generativer SOTA-KI-Modelle berichtet. Diese treten normalerweise in Form von Verlustspitzen auf. Beim PaLM-Modell von Google kam es beispielsweise während des Trainingsprozesses zu Instabilitäten. Numerische Voreingenommenheit ist die Hauptursache für diese Trainingsungenauigkeit.
