 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Zum ersten Mal über 70 % Karte! GeMap: Lokale hochpräzise Karte SOTA erneut aktualisiert
Zum ersten Mal über 70 % Karte! GeMap: Lokale hochpräzise Karte SOTA erneut aktualisiert
Zum ersten Mal über 70 % Karte! GeMap: Lokale hochpräzise Karte SOTA erneut aktualisiert
Oben geschrieben und persönliches Verständnis des Autors
Die Erstellung vektorisierter hochpräziser Karten auf der Grundlage von Sensordaten in Echtzeit ist für nachgelagerte Aufgaben wie Vorhersage und Planung von entscheidender Bedeutung und kann die schlechte Echtzeitleistung von Offline effektiv ausgleichen hochpräzise Karten. Mit der Entwicklung des Deep Learning ist nach und nach eine vektorisierte, hochpräzise Online-Kartenkonstruktion entstanden, und nach und nach sind repräsentative Werke wie HDMapNet, MapTR usw. entstanden. Allerdings fehlt es den bestehenden online vektorisierten hochpräzisen Kartenerstellungsmethoden an der Untersuchung der geometrischen Eigenschaften von Kartenelementen (einschließlich der Form von Elementen, vertikalen, parallelen und anderen geometrischen Beziehungen).
Geometrische Eigenschaften vektorisierter hochpräziser Karten
Vektorisierte hochpräzise Karten abstrahieren die Elemente auf der Straße stark und stellen jedes Kartenelement als zweidimensionale Punktfolge dar. Für die Gestaltung städtischer Straßen gelten in den meisten Fällen quadratische rechteckige oder Parallelogramme; in Straßenabschnitten, die nicht auseinanderlaufen und zusammenlaufen, sind zwei benachbarte Fahrspuren parallel zueinander . Verschiedene Elemente in hochauflösenden Karten weisen auch viele ähnliche Eigenschaften auf. Diese Regeln des gesunden Menschenverstandes werden in den geometrischen Eigenschaften von hochpräzisen Karten abstrahiert, einschließlich der Form von Kartenelementen (Rechteck, Parallelogramm, gerade Linie usw.). ) oder verschiedene Karten Beziehungen zwischen Elementen (parallel, vertikal usw.). Geometrische Eigenschaften schränken die Darstellung von Kartenelementen stark ein. Wenn Sie die geometrischen Eigenschaften der Online-Modellkonstruktion vollständig verstehen, können Sie genauere Ergebnisse erzielen.
Stellen Sie die Bedeutung der geometrischen Darstellung für hochpräzise Karten vor.
Obwohl es theoretisch immer noch für bestehende Modelle möglich ist, die geometrischen Eigenschaften von Kartenelementen zu lernen, bestimmen die Eigenschaften geometrischer Eigenschaften dies, zumindest unter herkömmlichen Methoden Design, das Modell ist nicht leicht zu erlernen.- Invarianz geometrischer Eigenschaften
absoluten Koordinaten der Kartenelemente (im Fahrzeugkoordinatensystem) weiterhin. Die Form von Fußgängerüberwegen, Fahrspuren, Straßenbegrenzungen usw. ändert sich nicht, ebenso wenig ändert sich die Parallelität zwischen den Fahrspuren. Die geometrischen Eigenschaften von Kartenelementen sind objektiv und eines ihrer wichtigen Merkmale ist die Invarianz. Genauer gesagt handelt es sich um eine starre Invarianz (die gegenüber Rotations- und Translationstransformationen invariant bleibt). Frühere Arbeiten basieren alle auf absoluten Koordinaten, unabhängig davon, ob sie eine einfache Polyliniendarstellung oder Polynomkurven mit Kontrollpunkten verwenden (z. B. Bézier-Kurven, stückweise Bézier-Kurven) und durchgängig auf der Grundlage der Optimierung absoluter Koordinaten. Das auf absoluten Koordinaten basierende Optimierungsziel weist selbst keine starre Invarianz auf, daher ist es schwierig zu erwarten, dass die lokal optimale Lösung, in die das Modell fällt, ein Verständnis der geometrischen Eigenschaften enthält. Daher ist eine Darstellung erforderlich, die die geometrischen Eigenschaften vollständig charakterisieren kann und eine gewisse Invarianz aufweist.
Abbildung 1. Beispiel für geometrische Invarianz. 
- Vielfalt geometrischer Eigenschaften
GeMap-Design
Geometrische Darstellung
Angesichts der beiden oben genannten Probleme verbessern wir zunächst die Darstellungsmethode. Wir hoffen, zusätzlich zur herkömmlichen, auf absoluten Koordinaten basierenden Darstellung eine gute geometrische Darstellung einzuführen, die die folgenden Anforderungen erfüllen muss:kann die
Form von Kartenelementen beschreiben- kann die
- Assoziation zwischen beschreiben Kartenelemente Starrheit
- Invarianz
- Um Translationsinvarianz sicherzustellen, verwenden wir eine relative Größe, d. und der Winkel
Um Formen zu beschreiben, berechnen wir den Abstand zwischen benachbarten Punkten in a Versatzvektoren einzelner Kartenelemente zwischen ihnen und berechnen Sie die Länge des Versatzvektors und den Winkel zwischen benachbarten Versatzvektoren. Diese Darstellung identifiziert jede Polylinie/Polygon eindeutig. Beispiele für zwei Bilder sind unten dargestellt:
Schauen Sie sich bitte Abbildung 2 an, die die Darstellung geometrischer Formen zeigt.
Ein Rechteck kann durch die Verwendung eines rechten Winkels und zweier Paare gleicher Seiten für eine gerade Linie beschrieben werden. Alle eingeschlossenen Winkel betragen 0 Grad oder 180 Grad .
Um die Assoziation zu charakterisieren, betrachten wir zunächst den Abstand zwischen zwei beliebigen Punkten. Wenn der Winkel jedoch für alle Punkt-zu-Punkt-Versatzvektoren berechnet wird, ist die Komplexität der Darstellung zu hoch und der Rechenaufwand unerschwinglich. Unter der Annahme, dass insgesamt Kartenelemente vorhanden sind und jedes Element durch einen Punkt dargestellt wird, wird die Datenmenge für alle Winkel erreicht (bei Annahme von 1000 wird davon ausgegangen, dass die Daten jedes Winkels eine 32-Bit-Gleitkommazahl sind, z. B eine Darstellung ist nur der belegte Platz wird das TB-Niveau erreichen). Tatsächlich ist dies für normale vertikale, parallele usw. Beziehungen nicht notwendig. Deshalb berechnen wir zunächst die Versätze innerhalb der Elemente und berechnen dann nur den Winkel zwischen jedem Paar dieser Versätze als Teil der geometrischen Darstellung. Diese vereinfachte Assoziationsdarstellung behält die Fähigkeit, parallele, vertikale und andere Beziehungen zu beschreiben, während die entsprechende Datenmenge nur (ungefähr 4 MB unter den oben genannten Bedingungen) beträgt. Zum besseren Verständnis stellen wir auch einige Beispiele zur Verfügung:
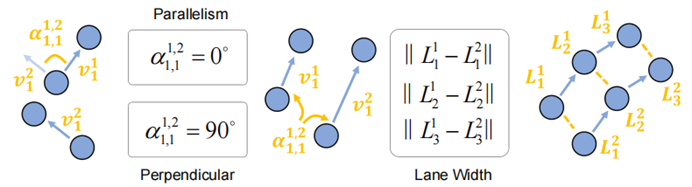
Abbildung 3. Geometrische Assoziationsdarstellung.
Die parallele Beziehung und die senkrechte Beziehung werden durch den Winkel zwischen dem Versatzvektor ausgedrückt, der 0 Grad oder 90 Grad beträgt; der Abstand zwischen den beiden Punkten kann bis zu einem gewissen Grad die Breiteninformationen der Fahrspur widerspiegeln.
Es ist die Darstellung von Bei der Optimierung geometrischer Formen und Assoziationen verwenden wir den einfachsten Ansatz: Berechnen Sie direkt die geometrische Darstellung der Vorhersage und Beschriftung und verwenden Sie dann die Norm als Optimierungsziel: Die Beschriftung und die Summe repräsentieren die berechnete Länge und den berechneten Winkel. Beim Umgang mit eingeschlossenen Winkeln wird ein Trick verwendet: Die direkte Berechnung des Winkels erfordert eine diskontinuierliche Arcustangensfunktion, die bei der Optimierung auf Schwierigkeiten stößt (in der Nähe von ±90 Grad gibt es ein verschwindendes Gradientenproblem). Was wir also tatsächlich vergleichen, ist der eingeschlossene Winkel Die Kosinuswerte und Sinus von Die Robustheit von
Geometrisch entkoppelter Aufmerksamkeit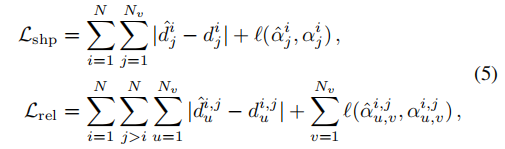
. Dies bedeutet, dass „die Entkopplung der Wahrnehmung von Form und Assoziation zu besseren Ergebnissen führen kann“. 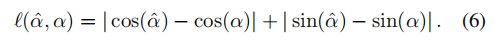
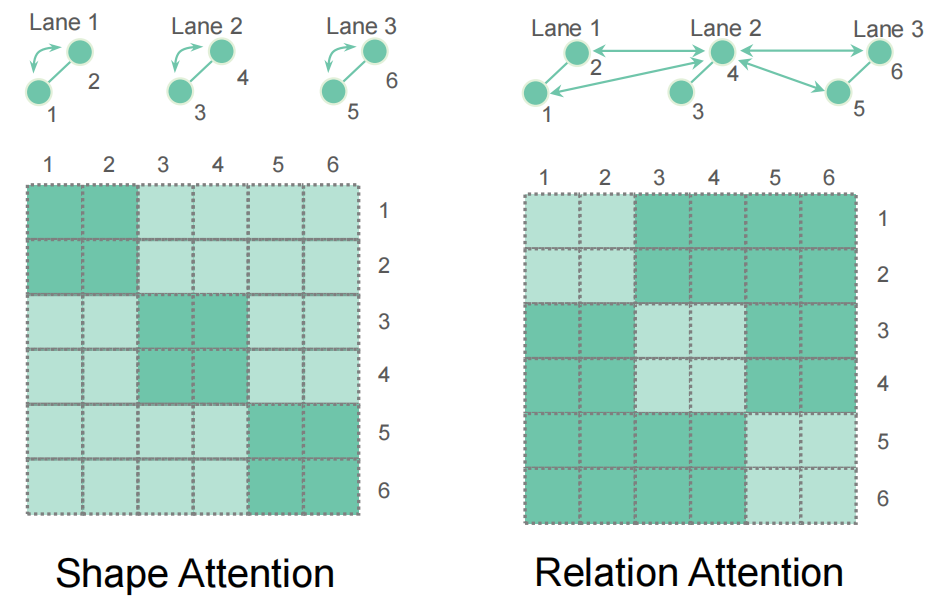
Jedes Kartenelement enthält Abfragen, und die Aufmerksamkeit wird innerhalb dieser
Abfragen zur Verarbeitung geometrischer Formen ausgeführt
und ergänzt die Aufmerksamkeitsbeziehungen zwischen Elementen Umgang mit geometrischen Assoziationen Die Aufmerksamkeit der geometrischen Entkopplung kann durch die folgende Abbildung anschaulicher dargestellt werden. Unsere Implementierung ist relativ einfach und verwendet Masken direkt, um den Aufmerksamkeitsbereich zu steuern. Da sich diese beiden Arten der Aufmerksamkeit bei angemessener Umsetzung ergänzen, kann die zeitliche Komplexität der Durchführung einer einzelnen Selbstaufmerksamkeit entsprechen
- Abbildung 4. Geometrisch entkoppelte Aufmerksamkeit.
- Die linke Seite ist die Formaufmerksamkeit, die innerhalb eines einzelnen Elements ausgeführt wird, und die rechte Seite ist die zugehörige Aufmerksamkeit, die zwischen Elementen ausgeführt wird. Experimentelle Ergebnisse
- Wir haben eine große Anzahl von Experimenten mit nuScenes- und Argoverse 2-Datensätzen durchgeführt. Bei beiden handelt es sich häufig um groß angelegte Datensätze zum autonomen Fahren, und beide bieten Kartenanmerkungen.
Wir haben drei Versuchsreihen mit nuScenes durchgeführt. Erstens verwenden wir eine relativ reine Kombination objektiver Funktionen, die nur geometrische Verluste und andere notwendige Verluste (wie Punkt-zu-Punkt-Abstand, Kantenrichtung, Klassifizierung) umfasst. Diese Kombination soll die Bedeutung der von uns vorgeschlagenen geometrischen Eigenschaften hervorheben. Mehrwert schaffen, ohne übermäßig SOTA-Ergebnisse zu verfolgen. Die Ergebnisse zeigen, dass unsere Methode in diesem Fall mAP im Vergleich zu MapTR verbessert. Um die Grenzen von GeMap zu erkunden, fügen wir auch einige Hilfsziele hinzu, darunter Segmentierung und Tiefenschätzung. In diesem Fall haben wir auch SOTA-Ergebnisse (mAP-Verbesserung) erzielt. Es ist erwähnenswert, dass das Erreichen einer solchen Verbesserung nicht zu große Einbußen bei der Inferenzgeschwindigkeit erfordert. Schließlich haben wir auch versucht, zusätzliche modale Eingaben von LiDAR einzuführen. Mithilfe zusätzlicher modaler Eingaben wurde die Leistung von GeMap weiter verbessert
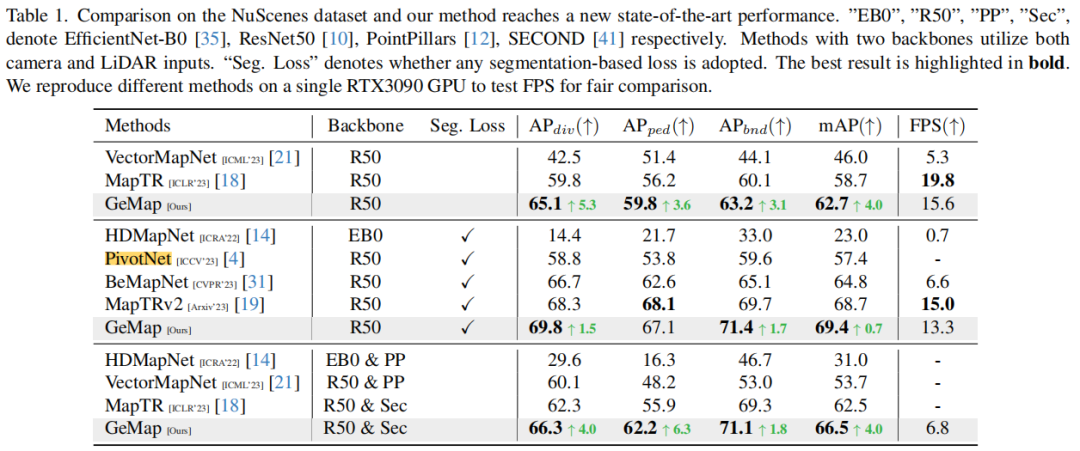
In ähnlicher Weise erzielte unsere Methode auch beim Argoverse 2-Datensatz sehr hervorragende Ergebnisse.

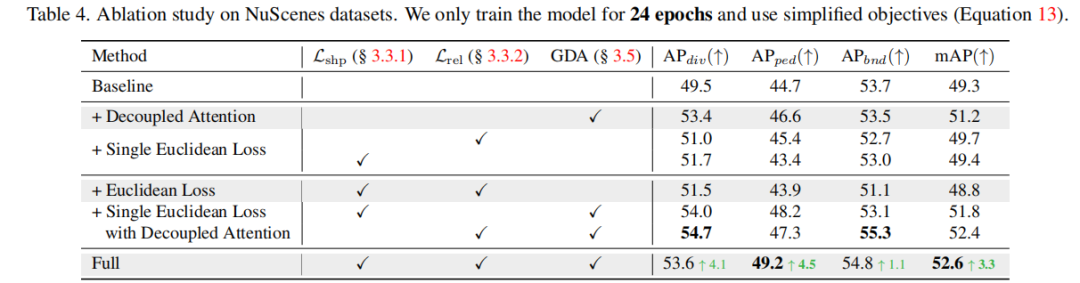
Der neu geschriebene Inhalt ist: Ablationsexperimente
Der weitere neugeschriebene Inhalt auf nuScenes ist: Ablationsexperimente beweisen den Wert von geometrischem Verlust und geometrisch entkoppelter Aufmerksamkeit. Interessanterweise führt die direkte Verwendung des geometrischen Verlusts, wie erwartet, zu einer Verringerung der Modellleistung. Wir glauben, dass dies daran liegt, dass die strukturelle Kopplung von Form und Assoziationsverarbeitung es dem Modell erschwert, die geometrische Darstellung zu optimieren. Nach der Kombination mit der geometrischen Entkopplungsaufmerksamkeit spielt der geometrische Verlust seine gebührende Rolle (von „+Euklidischer Verlust“ bis). "Voll").
Darüber hinaus haben wir auch eine visuelle Analyse von nuScenes durchgeführt. Aus den Visualisierungsergebnissen ist ersichtlich, dass GeMap nicht nur robust im Umgang mit Rotation und Translation ist, sondern auch bestimmte Vorteile bei der Lösung von Okklusionsproblemen aufweist, wie in der folgenden Abbildung dargestellt. Anspruchsvolle Kartenelemente sind in der Abbildung mit orangefarbenen Kästchen gekennzeichnet.
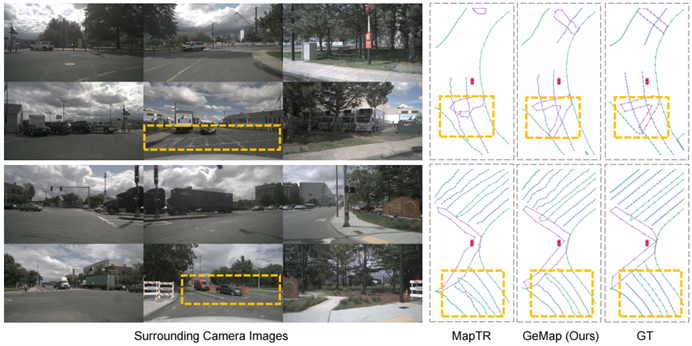 Abbildung 5. Visuelle Vergleichsergebnisse.
Abbildung 5. Visuelle Vergleichsergebnisse.
In den experimentellen Ergebnissen an Regentagen haben wir auch die Robustheit der Okklusion quantitativ überprüft (siehe Tabelle unten). Dies liegt daran, dass Regen die Kamera von Natur aus blockiert.
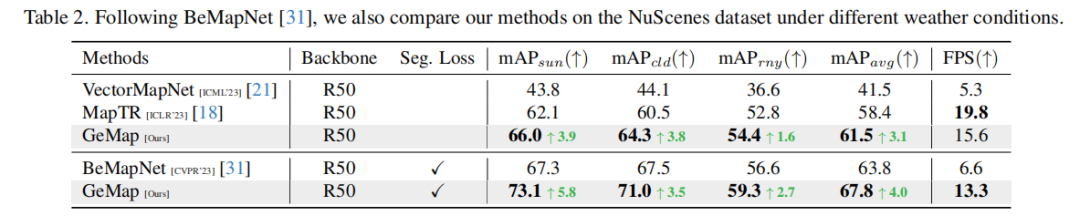 Dies kann dadurch erklärt werden, dass das Modell geometrische Eigenschaften lernt und daher Kartenelemente auch bei Verdeckungen besser erraten kann. Wenn das Modell beispielsweise die Form der Fahrspurlinien versteht, muss es nur einen Teil davon „sehen“, um den Rest abzuschätzen Selbst wenn einer von ihnen blockiert ist, kann der verdeckte Teil auch anhand der Parallelbeziehung und der Breitenfaktoren erraten werden . Auf dieser Grundlage schlagen wir eine leistungsstarke Methode vor, um diesen Wert zunächst zu überprüfen. Darüber hinaus könnte die Robustheit von GeMap gegenüber Okklusion auf die Idee hinweisen, geometrische Eigenschaften zur Bewältigung der Okklusion bei anderen autonomen Fahraufgaben (wie Erkennung, Belegungsvorhersage usw.) zu verwenden – da sowohl Fahrzeuge als auch Straßen relativ standardisierte geometrische Eigenschaften haben. Natürlich gibt es bei unserer Methode selbst noch viel zu erforschen. Können beispielsweise geometrische Elemente unterschiedlicher Komplexität mithilfe verschiedener Punkte adaptiv beschrieben werden? Ist es möglich, die geometrische Darstellung aus einer probabilistischen Perspektive zu verstehen und sie robuster gegenüber Rauschen zu machen? Gibt es eine bessere Darstellung der geometrischen Assoziation, weil wir die Elementzuordnung vereinfacht haben? Dies sind alles Richtungen für eine weitere Optimierung.
Dies kann dadurch erklärt werden, dass das Modell geometrische Eigenschaften lernt und daher Kartenelemente auch bei Verdeckungen besser erraten kann. Wenn das Modell beispielsweise die Form der Fahrspurlinien versteht, muss es nur einen Teil davon „sehen“, um den Rest abzuschätzen Selbst wenn einer von ihnen blockiert ist, kann der verdeckte Teil auch anhand der Parallelbeziehung und der Breitenfaktoren erraten werden . Auf dieser Grundlage schlagen wir eine leistungsstarke Methode vor, um diesen Wert zunächst zu überprüfen. Darüber hinaus könnte die Robustheit von GeMap gegenüber Okklusion auf die Idee hinweisen, geometrische Eigenschaften zur Bewältigung der Okklusion bei anderen autonomen Fahraufgaben (wie Erkennung, Belegungsvorhersage usw.) zu verwenden – da sowohl Fahrzeuge als auch Straßen relativ standardisierte geometrische Eigenschaften haben. Natürlich gibt es bei unserer Methode selbst noch viel zu erforschen. Können beispielsweise geometrische Elemente unterschiedlicher Komplexität mithilfe verschiedener Punkte adaptiv beschrieben werden? Ist es möglich, die geometrische Darstellung aus einer probabilistischen Perspektive zu verstehen und sie robuster gegenüber Rauschen zu machen? Gibt es eine bessere Darstellung der geometrischen Assoziation, weil wir die Elementzuordnung vereinfacht haben? Dies sind alles Richtungen für eine weitere Optimierung.
Der Inhalt, der neu geschrieben werden muss, ist: https://mp.weixin.qq.com/s/BoxlskT68Kjb07mfwQ7Swg Link
Das obige ist der detaillierte Inhalt vonZum ersten Mal über 70 % Karte! GeMap: Lokale hochpräzise Karte SOTA erneut aktualisiert. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1371
1371
 52
52
 So machen Sie Google Maps zur Standardkarte im iPhone
Apr 17, 2024 pm 07:34 PM
So machen Sie Google Maps zur Standardkarte im iPhone
Apr 17, 2024 pm 07:34 PM
Die Standardkarte auf dem iPhone ist Maps, Apples proprietärer Geolokalisierungsanbieter. Obwohl die Karte immer besser wird, funktioniert sie außerhalb der Vereinigten Staaten nicht gut. Im Vergleich zu Google Maps hat es nichts zu bieten. In diesem Artikel besprechen wir die möglichen Schritte, um Google Maps als Standardkarte auf Ihrem iPhone zu nutzen. So machen Sie Google Maps zur Standardkarte auf dem iPhone. Das Festlegen von Google Maps als Standardkarten-App auf Ihrem Telefon ist einfacher als Sie denken. Befolgen Sie die nachstehenden Schritte – Erforderliche Schritte – Sie müssen Gmail auf Ihrem Telefon installiert haben. Schritt 1 – Öffnen Sie den AppStore. Schritt 2 – Suchen Sie nach „Gmail“. Schritt 3 – Klicken Sie auf neben der Gmail-App
 Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Jan 17, 2024 pm 02:57 PM
Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Jan 17, 2024 pm 02:57 PM
Oben geschrieben und persönliches Verständnis des Autors. Dreidimensionales Gaussplatting (3DGS) ist eine transformative Technologie, die in den letzten Jahren in den Bereichen explizite Strahlungsfelder und Computergrafik entstanden ist. Diese innovative Methode zeichnet sich durch die Verwendung von Millionen von 3D-Gaußkurven aus, was sich stark von der Neural Radiation Field (NeRF)-Methode unterscheidet, die hauptsächlich ein implizites koordinatenbasiertes Modell verwendet, um räumliche Koordinaten auf Pixelwerte abzubilden. Mit seiner expliziten Szenendarstellung und differenzierbaren Rendering-Algorithmen garantiert 3DGS nicht nur Echtzeit-Rendering-Fähigkeiten, sondern führt auch ein beispielloses Maß an Kontrolle und Szenenbearbeitung ein. Dies positioniert 3DGS als potenziellen Game-Changer für die 3D-Rekonstruktion und -Darstellung der nächsten Generation. Zu diesem Zweck geben wir erstmals einen systematischen Überblick über die neuesten Entwicklungen und Anliegen im Bereich 3DGS.
 Wie lässt sich das Long-Tail-Problem in autonomen Fahrszenarien lösen?
Jun 02, 2024 pm 02:44 PM
Wie lässt sich das Long-Tail-Problem in autonomen Fahrszenarien lösen?
Jun 02, 2024 pm 02:44 PM
Gestern wurde ich während des Interviews gefragt, ob ich irgendwelche Long-Tail-Fragen gestellt hätte, also dachte ich, ich würde eine kurze Zusammenfassung geben. Das Long-Tail-Problem des autonomen Fahrens bezieht sich auf Randfälle bei autonomen Fahrzeugen, also mögliche Szenarien mit geringer Eintrittswahrscheinlichkeit. Das wahrgenommene Long-Tail-Problem ist einer der Hauptgründe, die derzeit den betrieblichen Designbereich intelligenter autonomer Einzelfahrzeugfahrzeuge einschränken. Die zugrunde liegende Architektur und die meisten technischen Probleme des autonomen Fahrens wurden gelöst, und die verbleibenden 5 % der Long-Tail-Probleme wurden nach und nach zum Schlüssel zur Einschränkung der Entwicklung des autonomen Fahrens. Zu diesen Problemen gehören eine Vielzahl fragmentierter Szenarien, Extremsituationen und unvorhersehbares menschliches Verhalten. Der „Long Tail“ von Randszenarien beim autonomen Fahren bezieht sich auf Randfälle in autonomen Fahrzeugen (AVs). Randfälle sind mögliche Szenarien mit geringer Eintrittswahrscheinlichkeit. diese seltenen Ereignisse
 Kamera oder Lidar wählen? Eine aktuelle Übersicht über die Erzielung einer robusten 3D-Objekterkennung
Jan 26, 2024 am 11:18 AM
Kamera oder Lidar wählen? Eine aktuelle Übersicht über die Erzielung einer robusten 3D-Objekterkennung
Jan 26, 2024 am 11:18 AM
0. Vorab geschrieben&& Persönliches Verständnis, dass autonome Fahrsysteme auf fortschrittlichen Wahrnehmungs-, Entscheidungs- und Steuerungstechnologien beruhen, indem sie verschiedene Sensoren (wie Kameras, Lidar, Radar usw.) verwenden, um die Umgebung wahrzunehmen, und Algorithmen und Modelle verwenden für Echtzeitanalysen und Entscheidungsfindung. Dies ermöglicht es Fahrzeugen, Verkehrszeichen zu erkennen, andere Fahrzeuge zu erkennen und zu verfolgen, das Verhalten von Fußgängern vorherzusagen usw. und sich so sicher an komplexe Verkehrsumgebungen anzupassen. Diese Technologie erregt derzeit große Aufmerksamkeit und gilt als wichtiger Entwicklungsbereich für die Zukunft des Transportwesens . eins. Aber was autonomes Fahren schwierig macht, ist herauszufinden, wie man dem Auto klarmachen kann, was um es herum passiert. Dies erfordert, dass der dreidimensionale Objekterkennungsalgorithmus im autonomen Fahrsystem Objekte in der Umgebung, einschließlich ihrer Standorte, genau wahrnehmen und beschreiben kann.
 Dieser Artikel reicht aus, um etwas über autonomes Fahren und Flugbahnvorhersage zu lesen!
Feb 28, 2024 pm 07:20 PM
Dieser Artikel reicht aus, um etwas über autonomes Fahren und Flugbahnvorhersage zu lesen!
Feb 28, 2024 pm 07:20 PM
Die Trajektorienvorhersage spielt eine wichtige Rolle beim autonomen Fahren. Unter autonomer Fahrtrajektorienvorhersage versteht man die Vorhersage der zukünftigen Fahrtrajektorie des Fahrzeugs durch die Analyse verschiedener Daten während des Fahrvorgangs. Als Kernmodul des autonomen Fahrens ist die Qualität der Trajektorienvorhersage von entscheidender Bedeutung für die nachgelagerte Planungssteuerung. Die Trajektorienvorhersageaufgabe verfügt über einen umfangreichen Technologie-Stack und erfordert Vertrautheit mit der dynamischen/statischen Wahrnehmung des autonomen Fahrens, hochpräzisen Karten, Fahrspurlinien, Fähigkeiten in der neuronalen Netzwerkarchitektur (CNN&GNN&Transformer) usw. Der Einstieg ist sehr schwierig! Viele Fans hoffen, so schnell wie möglich mit der Flugbahnvorhersage beginnen zu können und Fallstricke zu vermeiden. Heute werde ich eine Bestandsaufnahme einiger häufiger Probleme und einführender Lernmethoden für die Flugbahnvorhersage machen! Einführungsbezogenes Wissen 1. Sind die Vorschaupapiere in Ordnung? A: Schauen Sie sich zuerst die Umfrage an, S
 SIMPL: Ein einfacher und effizienter Multi-Agent-Benchmark zur Bewegungsvorhersage für autonomes Fahren
Feb 20, 2024 am 11:48 AM
SIMPL: Ein einfacher und effizienter Multi-Agent-Benchmark zur Bewegungsvorhersage für autonomes Fahren
Feb 20, 2024 am 11:48 AM
Originaltitel: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Paper-Link: https://arxiv.org/pdf/2402.02519.pdf Code-Link: https://github.com/HKUST-Aerial-Robotics/SIMPL Autor: Hong Kong University of Science und Technologie DJI-Papieridee: Dieses Papier schlägt eine einfache und effiziente Bewegungsvorhersagebasislinie (SIMPL) für autonome Fahrzeuge vor. Im Vergleich zum herkömmlichen Agent-Cent
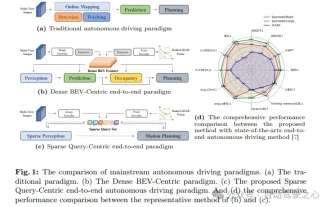 nuScenes' neuestes SOTA |. SparseAD: Sparse-Abfrage hilft effizientes durchgängiges autonomes Fahren!
Apr 17, 2024 pm 06:22 PM
nuScenes' neuestes SOTA |. SparseAD: Sparse-Abfrage hilft effizientes durchgängiges autonomes Fahren!
Apr 17, 2024 pm 06:22 PM
Vorab geschrieben und Ausgangspunkt Das End-to-End-Paradigma verwendet ein einheitliches Framework, um Multitasking in autonomen Fahrsystemen zu erreichen. Trotz der Einfachheit und Klarheit dieses Paradigmas bleibt die Leistung von End-to-End-Methoden für das autonome Fahren bei Teilaufgaben immer noch weit hinter Methoden für einzelne Aufgaben zurück. Gleichzeitig erschweren die in früheren End-to-End-Methoden weit verbreiteten Funktionen der dichten Vogelperspektive (BEV) die Skalierung auf mehr Modalitäten oder Aufgaben. Hier wird ein Sparse-Search-zentriertes End-to-End-Paradigma für autonomes Fahren (SparseAD) vorgeschlagen, bei dem die Sparse-Suche das gesamte Fahrszenario, einschließlich Raum, Zeit und Aufgaben, ohne dichte BEV-Darstellung vollständig abbildet. Insbesondere ist eine einheitliche, spärliche Architektur für die Aufgabenerkennung einschließlich Erkennung, Verfolgung und Online-Zuordnung konzipiert. Zudem schwer
 Sprechen wir über End-to-End- und autonome Fahrsysteme der nächsten Generation sowie über einige Missverständnisse über End-to-End-Autonomes Fahren?
Apr 15, 2024 pm 04:13 PM
Sprechen wir über End-to-End- und autonome Fahrsysteme der nächsten Generation sowie über einige Missverständnisse über End-to-End-Autonomes Fahren?
Apr 15, 2024 pm 04:13 PM
Im vergangenen Monat hatte ich aus bekannten Gründen einen sehr intensiven Austausch mit verschiedenen Lehrern und Mitschülern der Branche. Ein unvermeidliches Thema im Austausch ist natürlich End-to-End und der beliebte Tesla FSDV12. Ich möchte diese Gelegenheit nutzen, einige meiner aktuellen Gedanken und Meinungen als Referenz und Diskussion darzulegen. Wie definiert man ein durchgängiges autonomes Fahrsystem und welche Probleme sollten voraussichtlich durchgängig gelöst werden? Gemäß der traditionellsten Definition bezieht sich ein End-to-End-System auf ein System, das Rohinformationen von Sensoren eingibt und für die Aufgabe relevante Variablen direkt ausgibt. Bei der Bilderkennung kann CNN beispielsweise als End-to-End bezeichnet werden, verglichen mit der herkömmlichen Methode zum Extrahieren von Merkmalen + Klassifizieren. Bei autonomen Fahraufgaben werden Eingabedaten verschiedener Sensoren (Kamera/LiDAR) benötigt



