Einführung in SVG 2D in HTML5 6 – Überblick über das Fensterkoordinatensystem, das Benutzerkoordinatensystem und die Tutorialfähigkeiten zu transformation_html5

Koordinatensystem
SVG hat zwei Koordinatensysteme: das Fensterkoordinatensystem und das Benutzerkoordinatensystem. Standardmäßig stehen die Punkte im Benutzerkoordinatensystem und im Koordinatensystem des Ansichtsfensters in einer Eins-zu-Eins-Entsprechung, wobei der Ursprung in der oberen linken Ecke des Ansichtsfensters liegt, die x-Achse horizontal nach rechts verläuft und die y-Achse verläuft -Achse vertikal nach unten; wie in der Abbildung unten gezeigt:

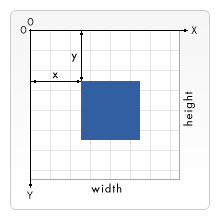
Die Fensterposition von SVG wird im Allgemeinen durch CSS angegeben und die Größe wird durch die Breiten- und Höhenattribute des SVG-Elements festgelegt. Wenn das SVG jedoch in einem eingebetteten Objekt (z. B. einem Objektelement oder einem anderen) gespeichert ist SVG-Element) und das Dokument, das die SVG-Datei enthält, mit CSS oder XSL formatiert ist und CSS oder andere angegebene Größenwerte dieser umgebenden Objekte bereits die Größe des Ansichtsfensters berechnen können, wird die Größe des umgebenden Objekts verwendet diesmal.

Hier müssen wir zwischen den Konzepten Fenster, Fensterkoordinatensystem und Benutzerkoordinatensystem unterscheiden:

Fenster: bezieht sich auf den sichtbaren rechteckigen Bereich auf der Webseite. Die Länge und Breite hängt im Allgemeinen von der Größe der umgebenden Objekte ab.

Koordinatensystem des Ansichtsfensters: Es handelt sich im Wesentlichen um ein Koordinatensystem mit einem Ursprung, einer x-Achse und einer y-Achse, das sich unendlich in zwei Richtungen erstreckt. Standardmäßig liegt der Ursprung in der oberen linken Ecke des Ansichtsfensters, die x-Achse verläuft horizontal nach rechts und die y-Achse verläuft vertikal nach unten. Punkte in diesem Koordinatensystem können transformiert werden.

Benutzerkoordinatensystem : Es handelt sich im Wesentlichen um ein Koordinatensystem mit einem Ursprung, einer x-Achse und einer y-Achse, das sich unendlich in zwei Richtungen erstreckt. Standardmäßig liegt der Ursprung in der oberen linken Ecke des Ansichtsfensters, die x-Achse verläuft horizontal nach rechts und die y-Achse verläuft vertikal nach unten. Punkte in diesem Koordinatensystem können transformiert werden.

Standardmäßig stimmt das Fensterkoordinatensystem mit dem Benutzerkoordinatensystem überein, es ist jedoch zu beachten, dass das Fensterkoordinatensystem zu dem Element gehört, das das Fenster erstellt. Nachdem das Fensterkoordinatensystem bestimmt wurde, wird der Koordinatenton des Das gesamte Fenster wird bestimmt. Das Benutzerkoordinatensystem gehört jedoch zu jedem Grafikelement. Solange die Grafik einer Koordinatentransformation unterzogen wird, wird ein neues Benutzerkoordinatensystem erstellt. Alle Koordinaten und Abmessungen in diesem Element verwenden dieses neue Benutzerkoordinatensystem.

Um es einfach auszudrücken: Das Fensterkoordinatensystem beschreibt das anfängliche Koordinatenprofil aller Elemente im Fenster, und das Benutzerkoordinatensystem beschreibt das Koordinatenprofil jedes Elements. Standardmäßig verwenden alle Elemente das Standardkoordinatensystem, das mit übereinstimmt das Fensterkoordinatensystem.

Koordinatenraumtransformation
Lassen Sie uns die Transformation der Leinwand-Benutzerkoordinaten überprüfen. Sie werden durch Übersetzungs-, Skalierungs- und Rotationsfunktionen implementiert Grafiken funktionieren, sofern sie nicht erneut transformiert werden, was dem Konzept des „aktuellen“ Benutzerkoordinatensystems entspricht. Canvas hat nur ein Benutzerkoordinatensystem.
In SVG ist die Situation völlig anders. SVG selbst ist ein Vektorgrafikelement, und seine beiden Koordinatensysteme können im Wesentlichen als „Benutzerkoordinatensysteme“ gezählt werden. Beide Koordinatenräume von SVG können transformiert werden: Fensterraumtransformation und Benutzerraumtransformation. Die Transformation des Fensterbereichs wird durch das viewBox-Attribut der relevanten Elemente gesteuert (diese Elemente erstellen neue Fenster); die Transformation des Benutzerbereichs wird durch das Transformationsattribut des Grafikelements gesteuert. Ansichtsraumtransformationen werden auf das entsprechende gesamte Ansichtsfenster angewendet, und Benutzerraumtransformationen werden auf das aktuelle Element und seine Unterelemente angewendet.

Ansichtsfenstertransformation – viewBox-Eigenschaft

Alle Elemente, die ein Fenster erstellen können (siehe nächster Abschnitt), sowie Markierungs-, Muster- und Ansichtselemente verfügen über ein viewBox-Attribut.

Das Format des viewBox-Attributwerts ist (x0, y0, u_width, u_height). Jeder Wert wird durch Kommas oder Leerzeichen getrennt. Zusammen bestimmen sie den vom Fenster angezeigten Bereich: die Koordinaten der oberen linken Ecke des Fensters sind auf (x0, y0) eingestellt, die Breite des Fensters ist auf u_width eingestellt und die Höhe ist u_height; diese Transformation wirkt sich auf das gesamte Fenster aus.

Lassen Sie sich hier nicht verwirren: Die Größe und Position des Fensters werden durch das Element bestimmt, das das Fenster erstellt, und die umgebenden Elemente (z. B. wird das Fenster, das durch das äußerste SVG-Element erstellt wird, durch CSS bestimmt). , Breite und Höhe), hier Die viewBox legt tatsächlich fest, welcher Teil des Ansichtsfenster-Koordinatensystems in diesem bestimmten Bereich angezeigt werden kann.
Die Einstellung von viewBox umfasst tatsächlich zwei Transformationen: Skalierung und Übersetzung des Ansichtsfensterbereichs.

Die Berechnung der Transformation ist ebenfalls sehr einfach: Nehmen Sie als Beispiel das Ansichtsfenster des äußersten SVG-Elements und gehen Sie davon aus, dass die Breite und Länge des SVG auf width, height und die viewBox auf (x0) eingestellt sind , y0, u_width, u_height). Dann sind die Skalierungsverhältnisse der Breite und Höhe der gezeichneten Grafiken: width/u_width bzw. height/u_height. Die Koordinaten der oberen linken Ecke des Fensters werden auf (x0,y0) gesetzt.

Erleben Sie den Unterschied in den Ergebnissen, die mit den folgenden Codes erzielt werden:

Kopieren Sie den Code

Der Code lautet wie folgt :

Im Bild oben sind grüne und rote Rechtecke zu sehen. In diesem Fall entsprechen die Punkte im Fensterkoordinatensystem immer noch eins zu eins. Dies ist auch die Standardsituation .

Code kopieren

Der Code lautet wie folgt:

Oben in dem durch das Beispiel gezeichneten Bild ist nur das grüne Rechteck zu sehen, und das auf dem Bildschirm angezeigte grüne Rechteck ist 200 * 200 Pixel groß. Zu diesem Zeitpunkt sind die Koordinatenpunkte keine Eins-zu-Eins-Entsprechung mehr. und das Bild wird vergrößert.

Code kopieren

Der Code lautet wie folgt:

In dem im obigen Beispiel gezeichneten Bild wird die Einheit des Fensterkoordinatensystems reduziert, sodass beide Rechtecke reduziert werden.

Bei der täglichen Arbeit besteht eine der Aufgaben, die wir häufig erledigen müssen, darin, eine Gruppe von Grafiken so zu skalieren, dass sie in den übergeordneten Container passt. Wir können dieses Ziel erreichen, indem wir das viewBox-Attribut festlegen.

Elemente, die neue Fenster erstellen
Wir können Fenster jederzeit verschachteln. Wenn ein neues Fenster erstellt wird, werden auch ein neues Fensterkoordinatensystem und ein Benutzerkoordinatensystem erstellt. Natürlich werden auch neue Beschneidungspfade erstellt. Im Folgenden finden Sie eine Liste von Elementen, die neue Fenster erstellen können:
svg: SVG unterstützt die Verschachtelung.
Symbol: Erstellt ein neues Fenster, wenn es durch das use-Element instanziiert wird.

Bild: Beim Verweis auf das SVG-Element wird ein neues Fenster erstellt.
foreignObject: Erstellen Sie ein neues Fenster, um die darin enthaltenen Objekte darzustellen.

Zoomverhältnis beibehalten – AspectRatio-Attribut beibehalten
Manchmal, insbesondere bei Verwendung von viewBox, erwarten wir, dass die Grafiken das gesamte Ansichtsfenster einnehmen, anstatt in beide Richtungen zu drücken Skalierung. Manchmal möchten wir, dass die Grafiken in beiden Richtungen in einem festen Verhältnis skaliert werden. Sie können dies mit dem Attribut „preserveAspectRatio“ steuern.
Dieses Attribut ist für alle Elemente verfügbar, die ein neues Fenster erstellen können, sowie für Bild-, Markierungs-, Muster- und Ansichtselemente. Und das Attribut „preserveAspectRatio“ wird erst wirksam, nachdem die „viewBox“ für das Element festgelegt wurde. Wenn die viewBox nicht festgelegt ist, wird das Attribut „preserveAspectRatio“ ignoriert.
Die Syntax des Attributs lautet wie folgt: preserveAspectRatio="[defer] []"
Beachten Sie, dass die drei Parameter durch Leerzeichen getrennt werden müssen.
defer: Optionaler Parameter, nur gültig für Bildelemente. Wenn der Wert des Attributs „preserveAspectRatio“ im Bildelement mit „defer“ beginnt, bedeutet dies, dass das Bildelement das Skalierungsverhältnis des referenzierten Elements verwendet Bild, wenn darauf verwiesen wird. Wenn das Bild keine Skalierung hat, wird „defer“ ignoriert. Alle anderen Elemente ignorieren diese Zeichenfolge.
align: Dieser Parameter bestimmt die Ausrichtung der einheitlichen Skalierung und kann die folgenden Werte annehmen:
none – erzwingt keine einheitliche Skalierung, sodass die Grafiken das gesamte Ansichtsfenster vollständig ausfüllen können.
xMinYMin – Erzwingt eine einheitliche Skalierung und richtet die in der ViewBox festgelegten Werte für an den minimalen X- und Y-Werten des Ansichtsfensters aus.
xMidYMin – Erzwingt eine gleichmäßige Skalierung und richtet den Mittelpunkt in X-Richtung der vivowBox am Mittelpunkt der X-Richtung im Ansichtsfenster aus. Kurz gesagt, der Mittelpunkt in X-Richtung ist gleich wie oben.
xMaxYMin – Erzwingt eine einheitliche Skalierung und richtet den in der ViewBox festgelegten Wert von auf den maximalen X-Wert des Ansichtsfensters aus.
Ähnlich wie bei anderen Wertetypen: xMinYMid, xMidYMid, xMaxYMid, xMinYMax, xMidYMax, xMaxYMax. Die Bedeutung dieser Kombinationen ist ähnlich wie oben.
meetOrSlice: optionaler Parameter, Sie können die folgenden Werte festlegen:
meet – der Standardwert, skaliert die Grafiken einheitlich, sodass alle Grafiken im Ansichtsfenster angezeigt werden.
Slice – Skalieren Sie die Grafiken gleichmäßig, sodass die Grafiken das Ansichtsfenster ausfüllen und die überschüssigen Teile abgeschnitten werden.

Das folgende Bild verdeutlicht die Wirkung verschiedener Füllungen:

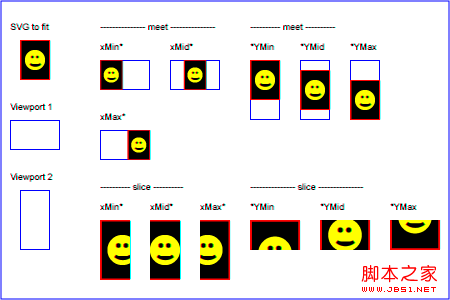
Transformation des Benutzerkoordinatensystems – Transformationsattribut
Diese Art der Transformation wird durch Festlegen des Transformationsattributs des Elements angegeben. Hierbei ist zu beachten, dass die Transformation des durch das Transformationsattribut festgelegten Elements nur das Element und seine Unterelemente betrifft und nichts mit anderen Elementen zu tun hat und sich nicht auf andere Elemente auswirkt.

Übersetzung – Übersetzen
Übersetzungstransformation übersetzt den relevanten Koordinatenwert in die angegebene Position. Diese Transformation erfordert die Übergabe des Übersetzungsbetrags auf beiden Achsen. Schauen Sie sich das Beispiel an:

Kopieren Sie den Code

Der Code lautet wie folgt:

In diesem Beispiel wird ein Rechteck gezeichnet und platziert seinen Startpunkt (0,0), übersetzt in (30,40). Obwohl die Koordinatenwerte von (x, y) direkt eingestellt werden können, ist es auch sehr praktisch, eine Übersetzungstransformation zu verwenden. Der zweite Parameter dieser Transformation kann weggelassen werden und wird standardmäßig als 0 behandelt.

Rotation – Drehen
Das Drehen eines Elements ist ebenfalls eine sehr häufige Aufgabe. Wir können die Rotationstransformation verwenden, um sie zu implementieren, was die Übergabe des Winkelparameters erfordert Drehung. Schauen Sie sich das Beispiel an:

Kopieren Sie den Code

Der Code lautet wie folgt:

In diesem Beispiel wird ein um 45 Grad gedrehtes Rechteck angezeigt. Es sind einige Punkte zu beachten:
1. Die Transformation verwendet hier den Winkelwert als Parameter.
2. Drehung bezieht sich auf die Drehung relativ zur x-Achse.
3. Die Drehung erfolgt um den Ursprung (0,0) des Benutzerkoordinatensystems.

skew - skew
Transformation unterstützt auch die Neigungstransformation, die entlang der x-Achse erfolgen kann (nach links und rechts neigen, ein positiver Winkel wird nach rechts geneigt, die tatsächlich die y-Achse kippt) oder eine Neigung entlang der y-Achse (nach oben und unten kippen, ein positiver Winkel bedeutet eine nach unten gerichtete Neigung, die tatsächlich die x-Achse kippt); diese Transformation erfordert die Übergabe eines Winkelparameters, der den Winkel von bestimmt Neigung. Schauen Sie sich das Beispiel unten an:

Kopieren Sie den Code

Der Code lautet wie folgt:

< rect x="30 " y="30" width="20" height="20" transform="skewX(45)" />

Aus dem Ergebnis können Sie direkt das gleiche Rechteck in verschiedenen Größen sehen Skew-Transformationen Schließlich werden Position und Form ermittelt. Beachten Sie hier, dass sich die Startposition des Rechtecks ​​geändert hat. Dies liegt daran, dass (30,30) sich bereits an einer anderen Position im neuen Koordinatensystem befindet.

Skalierung - Skalierung
Das Skalierungsobjekt wird durch die Skalierungstransformation vervollständigt, die zwei Parameter akzeptiert und die horizontalen bzw. vertikalen Skalierungsverhältnisse angibt Werden Parameter weggelassen, nimmt er denselben Wert wie der erste Parameter an. Schauen Sie sich das Beispiel unten an:

Kopieren Sie den Code

Der Code lautet wie folgt:

ABC (Skala)
< text x="50" y="50" font-size="20" transform="scale(1.5)">ABC (Skala)

Transformationsmatrix - Matrix
Jeder, der Grafik studiert hat, weiß, dass alle Transformationen tatsächlich durch Matrizen dargestellt werden, sodass die oben genannten Transformationen tatsächlich sein können verwendete eine 3*3-Matrix zur Darstellung von:

Kopieren Sie den Code

Der Code lautet wie folgt:

a c e
b d f
0 0 1

Da nur 6 Werte verwendet werden, wird es auch als [a b c d e f] abgekürzt. Durch Zuweisen von Matrix(a,b,c,d,e,f) zu transfrom kann die entsprechende Transformation implementiert werden. Bei der Transformation werden sowohl Koordinaten als auch Längen in neue Dimensionen umgewandelt. Die Matrizen, die den oben genannten verschiedenen Transformationen entsprechen, lauten wie folgt:

Übersetzungstransformation [1 0 1 0 tx ty]:

Code kopieren

Der Code lautet wie folgt:

1 0 tx
0 1 ty
0 0 1

Skalentransformation [sx 0 0 sy 0 0]:

Code kopieren

Der Code lautet wie folgt:

sx 0 0
0 sy 0
0 0 1

Rotationstransformation [cos(a) sin(a) -sin(a) cos(a) 0 0]:

Code kopieren

Der Code lautet wie folgt:

cos(a) -sin(a) 0
sin(a) cos(a) 0
00 1

Neigung entlang der 🎜>Der Code lautet wie folgt:

1 tan(a) 0

0 1 0 0 0 1Neigung entlang der Y-Achse [1 tan( a) 0 1 0 0]:

Code kopieren

Der Code lautet wie folgt:

11 0

tan(a) 1 000 1
Die Essenz der Transformation
Als wir zuvor Canvas zusammengefasst haben, wussten wir, dass verschiedene Transformationen auf das Benutzerkoordinatensystem wirken. In SVG gelten alle Transformationen auch für zwei Koordinatensysteme (im Wesentlichen „Benutzerkoordinatensysteme“). Wenn das Attribut „transform“ einem Containerobjekt oder Grafikobjekt oder das Attribut „viewBox“ einem „svg, symbol, marker, pattern, view“ zugewiesen wird, transformiert SVG entsprechend dem aktuellen Benutzerkoordinatensystem, um ein neues zu erstellen Benutzerkoordinatensystem und wirkt auf das aktuelle Objekt und seine Unterobjekte. Die im Objekt angegebenen Koordinaten und Längeneinheiten entsprechen nicht mehr im Verhältnis 1:1 dem Umfangskoordinatensystem, sondern werden in ein neues Benutzerkoordinatensystem umgewandelt, wobei die Verformung nur auf das aktuelle Element und dessen Elemente wirkt Unterelemente.

Transformationskette
Das Transformationsattribut unterstützt das Festlegen mehrerer Transformationen. Diese Transformationen müssen nur durch Leerzeichen getrennt und dann zusammen im Attribut platziert werden. Der Ausführungseffekt ist derselbe wie die unabhängige Ausführung dieser Transformationen nacheinander.

Code kopieren

Der Code lautet wie folgt:

Der obige Effekt ist derselbe wie der folgende:

Kopieren Sie den Code

Der Code lautet wie folgt:

< ;g transform="rotate(45) ">


< ;/g>
< /g>

Einheit
Lass uns endlich Sprechen Sie über die Einheit. Alle Koordinaten und Längen können ohne Einheiten angegeben werden.
Ohne Einheit

Werte ohne Einheiten gelten als „Benutzereinheiten“, bei denen es sich um die Einheitenwerte des aktuellen Benutzerkoordinatensystems handelt.
Mit Einheiten

Die relevanten Einheiten in SVG sind die gleichen wie in CSS: em, ex, px, pt, pc, cm, mm und in. Sie können für die Länge auch „%“ verwenden.
Relative Maßeinheiten: em und ex sind die gleichen wie in CSS, sie sind relativ zur Schriftgröße und x-Höhe der aktuellen Schriftart.
Absolute Maßeinheit: Ein px entspricht einer „Benutzereinheit“, d. h. „5px“ und „5“ sind gleich. Ob ein px jedoch einem Pixel entspricht, hängt davon ab, ob eine Transformation durchgeführt wurde.
Die anderen Einheiten sind grundsätzlich Vielfache von px: 1pt=1,25px, 1pc=15px, 1mm=3,543307px, 1cm=35,43307px, 1in=90px.

Wenn für die Breite und Höhe des äußersten SVG-Elements keine Einheit angegeben ist (d. h. „Benutzereinheit“), werden diese Werte als in px betrachtet.

Dieser Artikel ist etwas verwirrend. Denken Sie daran, dass „die Koordinaten und die Länge der Grafikelemente sich auf die Koordinaten und die Länge des neuen Benutzerkoordinatensystems nach der doppelten Transformation des Fensterkoordinatensystems beziehen.“ Transformation des Benutzerkoordinatensystems.“ Das ist es.

Praktische Referenz:
Skriptindex: http://msdn.microsoft.com/zh-cn/library/ff971910(v=vs.85).aspx
Entwicklungszentrum: https://developer.mozilla.org/en/SVG
Beliebte Referenz: http://www.chinasvg.com/
Offizielle Dokumentation: http://www.w3.org/TR/SVG11/