
(1). Die analytische Formel ist eine ganze Zahl und die unabhängige Variable kann eine beliebige reelle Zahl sein;
Für Brüche in analytischen Ausdrücken sollten die unabhängigen Variablen reelle Werte ungleich Null annehmen.(3) Für den Fall, dass der analytische Ausdruck ein quadratisches Radikal oder ein gerades Radikal ist, müssen wir die unabhängige Variable als reelle Zahl annehmen, deren Radikand nicht kleiner als 0 ist. Dadurch wird sichergestellt, dass der analytische Ausdruck sinnvoll und lösbar ist.
(4). Bei zusammengesetzten Funktionen mit komplexen funktionalen Analyseformeln sollte eine umfassende Überlegung angestellt werden, um sicherzustellen, dass jedes Element in der Analyseformel sinnvoll ist. Bevor wir Berechnungen durchführen, müssen wir den Bereich und den Wertebereich jeder Funktion sorgfältig analysieren, um sicherzustellen, dass der analytische Ausdruck der gesamten zusammengesetzten Funktion aussagekräftig ist. Dadurch werden Fehler oder Unsicherheiten bei den Berechnungen vermieden.
Beim Lösen von Gleichungen wie y=1/x+√(3x-1) müssen wir die tatsächliche Bedeutung der Funktion berücksichtigen und den Wertebereich der unabhängigen Variablen bestimmen. Für diese Gleichung sollte der Wertebereich ihrer unabhängigen Variablen x x ≥ 1/3,2 erfüllen, um sicherzustellen, dass die Funktion im praktischen Sinne sinnvoll ist. Auf diese Weise können wir Probleme besser lösen und die richtigen Ergebnisse erzielen.
Funktionsvariablen ähneln anderen Variablen wie Ganzzahlen. Sie haben keine praktische Bedeutung und werden nur zum Ersetzen des Ziels verwendet. Funktionsvariablen umfassen unabhängige Variablen und abhängige Variablen. Die unabhängige Variable ist eine Variable, die einen beliebigen Wert innerhalb eines bestimmten Wertebereichs (Definitionsbereich) annimmt, während die abhängige Variable die Variable ist, die erhalten wird, nachdem die unabhängige Variable gemäß der Funktionsregel einen Wert annimmt.
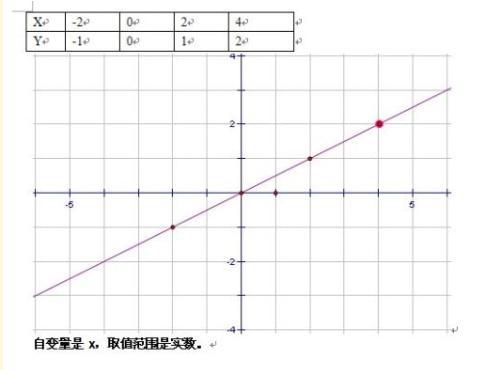
Der Wertebereich der unabhängigen Variablen bezieht sich auf alle Werte der unabhängigen Variablen in der Funktion, die sie sinnvoll machen. In der Mathematik definieren wir einen Wertebereich für die Argumente einer Funktion, um sicherzustellen, dass die Funktion innerhalb dieses Bereichs sinnvoll ist. Dieser Bereich kann je nach Definition und Anforderungen der Funktion die Menge reeller Zahlen, ganzer Zahlen, rationaler Zahlen oder anderer spezifischer numerischer Bereiche sein.
So bestimmen Sie den Wertebereich der unabhängigen Variablen:
Zunächst müssen wir den Wertebereich der unabhängigen Variablen berücksichtigen, um sicherzustellen, dass der analytische Ausdruck aussagekräftig ist. Wenn der analytische Ausdruck eine ganze Zahl ist, kann die unabhängige Variable eine beliebige reelle Zahl sein. Und wenn der analytische Ausdruck in Bruchform vorliegt, müssen wir sicherstellen, dass der Nenner nicht Null ist, sodass der Wertebereich der unabhängigen Variablen alle reellen Zahlen umfasst, die den Nenner ungleich Null machen. Durch die sinnvolle Wahl des Wertebereichs der unabhängigen Variablen können wir die Gültigkeit des analytischen Ausdrucks sicherstellen.
Wenn der analytische Ausdruck eine Quadratwurzel enthält, müssen Sie sicherstellen, dass der Radikand nicht kleiner als die reelle Zahl Null ist, damit Sie eine gültige Lösung erhalten. Wenn funktionale analytische Ausdrücke zur Darstellung tatsächlicher Probleme verwendet werden, müssen die Werte der unabhängigen Variablen das tatsächliche Problem sinnvoll machen, um die Rationalität der Ergebnisse sicherzustellen. Auf diese Weise können wir den Wertebereich der unabhängigen Variablen basierend auf diesen beiden Prinzipien bestimmen, um die richtige Antwort zu erhalten.
Der Wertebereich der unabhängigen Variablen kann unendlich, endlich oder eine einzelne (oder mehrere) Zahl sein. Wenn ein analytischer Ausdruck einer Funktion mehrere algebraische Ausdrücke enthält, sollte der Wertebereich der unabhängigen Variablen der Funktion der gemeinsame Teil des Wertebereichs der unabhängigen Variablen in jedem algebraischen Ausdruck sein.
Funktionsvariablen und praktische Probleme:
Bei der Lösung praktischer Probleme stoßen wir häufig auf die Konzepte von Variablen und Konstanten. Variablen und Konstanten sind oft relativ und ihre Identitäten können in verschiedenen Forschungsprozessen ineinander umgewandelt werden. Bei der Bearbeitung praktischer Probleme müssen wir jedoch auf die Unterscheidung zwischen Variablen und Konstanten achten. Variablen können sich ändern, während Konstanten fest sind. Daher müssen wir von Fall zu Fall bestimmen, wann Variablen und Konstanten verwendet werden sollen, und sie während des Rätsellösungsprozesses flexibel verwenden.
Als nächstes können wir versuchen, Verbindungen zwischen Variablen zu finden und lernen, wie wir Funktionen verwenden, um sie darzustellen. Auf diese Weise können wir Rätsel besser lösen und Wege finden, Levels zu bestehen.
Bei der Lösung praktischer Probleme ist es sehr wichtig, den Funktionsgraphen zu verwenden. Wir müssen die Bedeutung der horizontalen und vertikalen Achsen richtig verstehen, die Eigenschaften von Funktionsgraphen verstehen und in der Lage sein, Bilder genau zu identifizieren und zur Lösung von Problemen zu verwenden. Durch diese Methode können wir die Eigenschaften und das Verhalten von Funktionen besser verstehen und so verschiedene praktische Probleme effektiver lösen.
Referenz: Sogou-Enzyklopädie – Funktionsvariablen
So bestimmen Sie den Wertebereich unabhängiger Variablen in Funktionsausdrücken
1. Verwandte Funktionskonzepte:
Im Allgemeinen werden wir zwei Variablen x und y in einen bestimmten Änderungsprozess einbeziehen. Wenn es für jeden spezifischen Wert von x innerhalb eines bestimmten Bereichs einen eindeutigen entsprechenden y-Wert gibt, dann sagen wir, dass y eine Funktion von x ist und x eine unabhängige Variable genannt wird.
Die Bedeutung von Funktionen sollte unter folgenden Gesichtspunkten verstanden werden:
Wenn wir einen bestimmten Veränderungsprozess untersuchen, untersuchen wir die funktionale Beziehung zwischen zwei Variablen. In verschiedenen Forschungsprozessen können Variablen und Konstanten ineinander umgewandelt werden, das heißt, Konstanten und Variablen beziehen sich auf einen bestimmten Prozess. Diese Flexibilität bei der gegenseitigen Konvertierung ermöglicht es uns, die Beziehung zwischen Variablen besser zu verstehen und zu analysieren.
(2) Der Wertebereich der Variablen x setzt sich aus allen zulässigen Werten zusammen. (3) Es gibt eine eindeutige Entsprechung zwischen den Variablen x und y, das heißt, für jeden zulässigen Wert von x gibt es einen ihm entsprechenden eindeutigen y-Wert.
So verstehen Sie die gleiche Funktion:
Das Konzept der Funktion kann so verstanden werden, dass zwischen der Variablen x und der Variablen y eine spezielle Entsprechung besteht (dh die entsprechende Regel) und jeder x-Wert innerhalb des Wertebereichs der Variablen x einem eindeutigen y-Wert entspricht Die Variable y ist eine Funktion der Variablen x. Kurz gesagt umfasst der Funktionsbegriff die folgenden zwei Hauptpunkte:
(1) Funktionale Beziehung zwischen y und x;
(2) Der Wertebereich der unabhängigen Variablen x in der funktionalen Beziehung.Dies bedeutet, dass dieselbe Funktion die beiden oben genannten Aspekte erfüllen muss, das heißt, der funktionale Beziehungsausdruck ist derselbe (oder derselbe nach der Verformung) und der Wertebereich der unabhängigen Variablen x ist auch derselbe nicht die gleiche Funktion. Es ist einfacher zu erkennen, ob die funktionalen Beziehungsausdrücke gleich sind oder nicht, und der Wertebereich der unabhängigen Variablen x kann manchmal leicht übersehen werden. Bitte beachten Sie diesen Punkt.
Unter den folgenden Funktionen ist () diejenige mit der gleichen funktionalen Beziehung wie y=x.
Rätsellösungsmethode: Zuerst müssen wir die analytischen Ausdrücke der vier Funktionen vereinfachen und sie mit y=x vergleichen, um zu sehen, ob sie gleich sind. Dann müssen wir den Wertebereich der unabhängigen Variablen x in jeder Funktion bestimmen und ihn mit dem analytischen Ausdruck von y=x und dem Wertebereich der unabhängigen Variablen x vergleichen. Es ist nur dann die gleiche Funktion, wenn beide Bedingungen erfüllt sind.
Lösung: Funktion y=x, der Wertebereich ihrer unabhängigen Variablen x sind alle reellen Zahlen.
Der Wertebereich seiner unabhängigen Variablen x umfasst alle reellen Zahlen x≥0.
, der Wertebereich seiner unabhängigen Variablen x sind alle reellen Zahlen x≠0.
, der Wertebereich seiner unabhängigen Variablen x sind alle reellen Zahlen.
, der Wertebereich seiner unabhängigen Variablen x sind alle reellen Zahlen.
Natürlich hat nur die analytische Formel der Option (C) den gleichen Wertebereich wie y=x, daher sollte die richtige Antwort (C) sein.
2. Der Wertebereich des Funktionsarguments
Das Prinzip des Wertebereichs von Funktionsargumenten ist:
(1) Die analytische Formel ist eine ganze Zahl und die unabhängige Variable kann jede reelle Zahl annehmen.
Der analytische Ausdruck ist ein Bruch. Wenn Sie also den Wert der unabhängigen Variablen bestimmen, müssen Sie vermeiden, dass der Nenner gleich Null wird. Dies liegt daran, dass ein Nullnenner den Bruch unberechenbar macht. Stellen Sie sicher, dass der Nenner des analytischen Ausdrucks ungleich Null ist, um eine gültige Lösung zu erhalten.
In Fällen, in denen der analytische Ausdruck irrational ist, müssen wir die folgenden zwei Punkte beachten: 1. Wenn es sich um ein quadratisches Radikal handelt, muss der Wert des Radikals größer oder gleich Null sein. Daher müssen wir den Wertebereich der unabhängigen Variablen so finden, dass der Modul größer oder gleich Null ist. 2. Wenn es sich um ein kubisches Radikal handelt, kann die unabhängige Variable eine beliebige reelle Zahl sein. Das bedeutet, dass wir jede beliebige reelle Zahl als Wert der unabhängigen Variablen wählen können. Diese Überlegungen werden uns helfen, irrationale Ausdrücke richtig zu analysieren und den Wertebereich für die unabhängigen Variablen zu bestimmen.
Wenn der analytische Ausdruck aus den oben genannten Formen synthetisiert wird, muss der Wertebereich der unabhängigen Variablen gleichzeitig ihre jeweiligen Bedingungen erfüllen. So können wir Probleme besser lösen.
3. Funktionswert
Probleme im Zusammenhang mit Funktionswerten können in die Werte algebraischer Ausdrücke umgewandelt werden.
4. Funktionsgraph
Funktionsgrafiken realisieren die gegenseitige Transformation zwischen Zahlen und Formen.
Das obige ist der detaillierte Inhalt vonSo bestimmen Sie den Wertebereich unabhängiger Variablen in einer Funktion. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Welche Software ist Zoom?
Welche Software ist Zoom?
 MySQL-Index
MySQL-Index
 Warum gibt es nach dem Einschalten des Computers kein Signal auf dem Monitor?
Warum gibt es nach dem Einschalten des Computers kein Signal auf dem Monitor?
 Die Rolle des Basis-Tags
Die Rolle des Basis-Tags
 Einführung in Festplattenschnittstellentypen
Einführung in Festplattenschnittstellentypen
 So verwenden Sie Google Voice
So verwenden Sie Google Voice
 Der Unterschied zwischen dem selbst betriebenen Flagship-Store von JD.com und seinem offiziellen Flagship-Store
Der Unterschied zwischen dem selbst betriebenen Flagship-Store von JD.com und seinem offiziellen Flagship-Store
 Was macht Matcha Exchange?
Was macht Matcha Exchange?




