 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Verstehen Sie die Kernfunktionen von Pytorch genau: automatische Ableitung!
Verstehen Sie die Kernfunktionen von Pytorch genau: automatische Ableitung!
Verstehen Sie die Kernfunktionen von Pytorch genau: automatische Ableitung!
Hallo, ich bin Xiaozhuang!
Über den automatischen Ableitungsvorgang in Pytorch stellen wir das Konzept der automatischen Ableitung in Pytorch vor.
Die automatische Ableitung ist eine wichtige Funktion des Deep-Learning-Frameworks, die zur Berechnung von Gradienten und zur Erzielung von Parameteraktualisierungen und -optimierungen verwendet wird.
PyTorch ist ein häufig verwendetes Deep-Learning-Framework, das dynamische Berechnungsdiagramme und automatische Ableitungsmechanismen verwendet, um den Gradientenberechnungsprozess zu vereinfachen.

Automatische Ableitung
Automatische Ableitung ist eine wichtige Funktion des Machine-Learning-Frameworks. Sie kann die Ableitung (Gradient) einer Funktion automatisch berechnen und so den Prozess des Trainings von Deep-Learning-Modellen vereinfachen. Beim Deep Learning enthalten Modelle oft eine große Anzahl von Parametern und die manuelle Berechnung von Gradienten kann komplex und fehleranfällig werden. PyTorch bietet eine automatische Ableitungsfunktion, mit der Benutzer problemlos Gradienten berechnen und Backpropagation durchführen können, um Modellparameter zu aktualisieren. Die Einführung dieser Funktion verbessert die Effizienz und Benutzerfreundlichkeit von Deep Learning erheblich.
Ein kleines Prinzip
Die automatische Ableitungsfunktion von PyTorch basiert auf dynamischen Berechnungsdiagrammen. Ein Berechnungsdiagramm ist eine Diagrammstruktur, die zur Darstellung des Funktionsberechnungsprozesses verwendet wird, wobei Knoten Operationen und Kanten den Datenfluss darstellen. Im Gegensatz zu statischen Berechnungsdiagrammen kann die Struktur dynamischer Berechnungsdiagramme dynamisch basierend auf dem tatsächlichen Ausführungsprozess generiert werden, anstatt im Voraus definiert zu werden. Dieses Design macht PyTorch flexibel und skalierbar, um sich an unterschiedliche Computeranforderungen anzupassen. Durch dynamische Berechnungsdiagramme kann PyTorch den Verlauf von Vorgängen aufzeichnen, Backpropagation durchführen und bei Bedarf Gradienten berechnen. Damit ist PyTorch eines der am weitesten verbreiteten Frameworks im Bereich Deep Learning.
In PyTorch wird jede Aktion des Benutzers aufgezeichnet, um das Berechnungsdiagramm zu erstellen. Wenn der Gradient berechnet werden muss, kann PyTorch auf diese Weise eine Rückausbreitung gemäß dem Berechnungsdiagramm durchführen und automatisch den Gradienten jedes Parameters zur Verlustfunktion berechnen. Dieser auf dynamischen Berechnungsdiagrammen basierende automatische Ableitungsmechanismus macht PyTorch flexibel und skalierbar und eignet sich daher für verschiedene komplexe neuronale Netzwerkstrukturen.
Grundlegende Operationen für die automatische Ableitung
1. Tensor
In PyTorch ist Tensor die grundlegende Datenstruktur für die automatische Ableitung. Tensoren ähneln mehrdimensionalen Arrays in NumPy, verfügen jedoch über zusätzliche Funktionen wie die automatische Ableitung. Über die Torch.Tensor-Klasse können Benutzer Tensoren erstellen und verschiedene Operationen an ihnen ausführen.
import torch# 创建张量x = torch.tensor([2.0], requires_grad=True)
Im obigen Beispiel bedeutet require_grad=True, dass wir diesen Tensor automatisch differenzieren wollen.
2. Erstellung eines Computergraphen
Jede ausgeführte Operation erstellt einen Knoten im Computergraphen. PyTorch bietet verschiedene Tensoroperationen wie Addition, Multiplikation, Aktivierungsfunktionen usw., die Spuren im Berechnungsdiagramm hinterlassen.
# 张量操作y = x ** 2z = 2 * y + 3
Im obigen Beispiel werden die Berechnungsvorgänge von y und z im Berechnungsdiagramm aufgezeichnet.
3. Gradientenberechnung und Backpropagation
Sobald das Berechnungsdiagramm erstellt ist, kann die Backpropagation durchgeführt werden, indem die Methode .backward() aufgerufen wird, um den Gradienten automatisch zu berechnen.
# 反向传播z.backward()
An diesem Punkt kann der Gradient von x durch Zugriff auf x.grad ermittelt werden.
# 获取梯度print(x.grad)
4. Gradientenverfolgung deaktivieren
Manchmal möchten wir die Gradientenverfolgung für bestimmte Vorgänge deaktivieren. Dazu können wir den Kontextmanager Torch.no_grad() verwenden.
with torch.no_grad():# 在这个区域内的操作不会被记录在计算图中w = x + 1
5. Gradienten löschen
In der Trainingsschleife ist es normalerweise notwendig, die Gradienten vor jeder Backpropagation zu löschen, um eine Gradientenakkumulation zu vermeiden.
# 清零梯度x.grad.zero_()
Ein vollständiger Fall: automatische Ableitung der linearen Regression
Um den Prozess der automatischen Ableitung genauer zu demonstrieren, betrachten wir ein einfaches lineares Regressionsproblem. Wir definieren ein lineares Modell und eine mittlere quadratische Fehlerverlustfunktion und verwenden eine automatische Ableitung, um die Modellparameter zu optimieren.
import torch# 数据准备X = torch.tensor([[1.0], [2.0], [3.0]])y = torch.tensor([[2.0], [4.0], [6.0]])# 模型参数w = torch.tensor([[0.0]], requires_grad=True)b = torch.tensor([[0.0]], requires_grad=True)# 模型和损失函数def linear_model(X, w, b):return X @ w + bdef mean_squared_error(y_pred, y_true):return ((y_pred - y_true) ** 2).mean()# 训练循环learning_rate = 0.01epochs = 100for epoch in range(epochs):# 前向传播y_pred = linear_model(X, w, b)loss = mean_squared_error(y_pred, y)# 反向传播loss.backward()# 更新参数with torch.no_grad():w -= learning_rate * w.gradb -= learning_rate * b.grad# 清零梯度w.grad.zero_()b.grad.zero_()# 打印最终参数print("训练后的参数:")print("权重 w:", w)print("偏置 b:", b)In diesem Beispiel definieren wir ein einfaches lineares Modell und eine mittlere quadratische Fehlerverlustfunktion. Durch mehrere iterative Trainingsschleifen werden die Parameter w und b des Modells optimiert, um die Verlustfunktion zu minimieren.
Endlich
Die automatische Ableitung in PyTorch bietet leistungsstarke Unterstützung für Deep Learning und macht das Modelltraining einfacher und effizienter.
Durch dynamische Berechnungsdiagramme und Gradientenberechnungen können Benutzer problemlos komplexe neuronale Netzwerkstrukturen definieren und Optimierungsalgorithmen wie den Gradientenabstieg durch automatische Ableitung implementieren.
Dadurch können sich Deep-Learning-Forscher und Ingenieure mehr auf Modelldesign und Experimente konzentrieren, ohne sich um die Details von Gradientenberechnungen kümmern zu müssen.
Das obige ist der detaillierte Inhalt vonVerstehen Sie die Kernfunktionen von Pytorch genau: automatische Ableitung!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 iFlytek: Die Fähigkeiten des Ascend 910B von Huawei sind grundsätzlich mit denen des A100 von Nvidia vergleichbar, und sie arbeiten zusammen, um eine neue Basis für die allgemeine künstliche Intelligenz meines Landes zu schaffen
Oct 22, 2023 pm 06:13 PM
iFlytek: Die Fähigkeiten des Ascend 910B von Huawei sind grundsätzlich mit denen des A100 von Nvidia vergleichbar, und sie arbeiten zusammen, um eine neue Basis für die allgemeine künstliche Intelligenz meines Landes zu schaffen
Oct 22, 2023 pm 06:13 PM
Diese Website berichtete am 22. Oktober, dass iFlytek im dritten Quartal dieses Jahres einen Nettogewinn von 25,79 Millionen Yuan erzielte, was einem Rückgang von 81,86 % gegenüber dem Vorjahr entspricht; der Nettogewinn in den ersten drei Quartalen betrug 99,36 Millionen Yuan Rückgang um 76,36 % gegenüber dem Vorjahr. Jiang Tao, Vizepräsident von iFlytek, gab bei der Leistungsbesprechung im dritten Quartal bekannt, dass iFlytek Anfang 2023 ein spezielles Forschungsprojekt mit Huawei Shengteng gestartet und gemeinsam mit Huawei eine leistungsstarke Betreiberbibliothek entwickelt hat, um gemeinsam eine neue Basis für Chinas allgemeine künstliche Intelligenz zu schaffen Intelligenz, die den Einsatz inländischer Großmodelle ermöglicht. Die Architektur basiert auf unabhängig innovativer Soft- und Hardware. Er wies darauf hin, dass die aktuellen Fähigkeiten des Huawei Ascend 910B grundsätzlich mit dem A100 von Nvidia vergleichbar seien. Auf dem bevorstehenden iFlytek 1024 Global Developer Festival werden iFlytek und Huawei weitere gemeinsame Ankündigungen zur Rechenleistungsbasis für künstliche Intelligenz machen. Er erwähnte auch,
 Die perfekte Kombination aus PyCharm und PyTorch: detaillierte Installations- und Konfigurationsschritte
Feb 21, 2024 pm 12:00 PM
Die perfekte Kombination aus PyCharm und PyTorch: detaillierte Installations- und Konfigurationsschritte
Feb 21, 2024 pm 12:00 PM
PyCharm ist eine leistungsstarke integrierte Entwicklungsumgebung (IDE) und PyTorch ist ein beliebtes Open-Source-Framework im Bereich Deep Learning. Im Bereich maschinelles Lernen und Deep Learning kann die Verwendung von PyCharm und PyTorch für die Entwicklung die Entwicklungseffizienz und Codequalität erheblich verbessern. In diesem Artikel wird detailliert beschrieben, wie PyTorch in PyCharm installiert und konfiguriert wird, und es werden spezifische Codebeispiele angehängt, um den Lesern zu helfen, die leistungsstarken Funktionen dieser beiden besser zu nutzen. Schritt 1: Installieren Sie PyCharm und Python
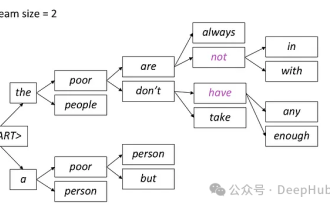 Einführung in fünf Stichprobenmethoden bei Aufgaben zur Generierung natürlicher Sprache und bei der Implementierung von Pytorch-Code
Feb 20, 2024 am 08:50 AM
Einführung in fünf Stichprobenmethoden bei Aufgaben zur Generierung natürlicher Sprache und bei der Implementierung von Pytorch-Code
Feb 20, 2024 am 08:50 AM
Bei Aufgaben zur Generierung natürlicher Sprache ist die Stichprobenmethode eine Technik, um eine Textausgabe aus einem generativen Modell zu erhalten. In diesem Artikel werden fünf gängige Methoden erläutert und mit PyTorch implementiert. 1. GreedyDecoding Bei der Greedy-Decodierung sagt das generative Modell die Wörter der Ausgabesequenz basierend auf der Eingabesequenz Zeit Schritt für Zeit voraus. In jedem Zeitschritt berechnet das Modell die bedingte Wahrscheinlichkeitsverteilung jedes Wortes und wählt dann das Wort mit der höchsten bedingten Wahrscheinlichkeit als Ausgabe des aktuellen Zeitschritts aus. Dieses Wort wird zur Eingabe für den nächsten Zeitschritt und der Generierungsprozess wird fortgesetzt, bis eine Abschlussbedingung erfüllt ist, beispielsweise eine Sequenz mit einer bestimmten Länge oder eine spezielle Endmarkierung. Das Merkmal von GreedyDecoding besteht darin, dass die aktuelle bedingte Wahrscheinlichkeit jedes Mal die beste ist
 Implementierung eines Rauschentfernungs-Diffusionsmodells mit PyTorch
Jan 14, 2024 pm 10:33 PM
Implementierung eines Rauschentfernungs-Diffusionsmodells mit PyTorch
Jan 14, 2024 pm 10:33 PM
Bevor wir das Funktionsprinzip des Denoising Diffusion Probabilistic Model (DDPM) im Detail verstehen, wollen wir zunächst einige Aspekte der Entwicklung generativer künstlicher Intelligenz verstehen, die auch zu den Grundlagenforschungen von DDPM gehört. VAEVAE verwendet einen Encoder, einen probabilistischen latenten Raum und einen Decoder. Während des Trainings sagt der Encoder den Mittelwert und die Varianz jedes Bildes voraus und tastet diese Werte aus einer Gaußschen Verteilung ab. Das Ergebnis der Abtastung wird an den Decoder weitergeleitet, der das Eingabebild in eine dem Ausgabebild ähnliche Form umwandelt. Zur Berechnung des Verlusts wird die KL-Divergenz verwendet. Ein wesentlicher Vorteil von VAE ist die Fähigkeit, vielfältige Bilder zu erzeugen. In der Abtastphase kann man direkt aus der Gaußschen Verteilung Stichproben ziehen und über den Decoder neue Bilder erzeugen. GAN hat in nur einem Jahr große Fortschritte bei Variational Autoencodern (VAEs) gemacht.
 Tutorial zur Installation von PyCharm mit PyTorch
Feb 24, 2024 am 10:09 AM
Tutorial zur Installation von PyCharm mit PyTorch
Feb 24, 2024 am 10:09 AM
Als leistungsstarkes Deep-Learning-Framework wird PyTorch häufig in verschiedenen maschinellen Lernprojekten eingesetzt. Als leistungsstarke integrierte Python-Entwicklungsumgebung kann PyCharm auch bei der Umsetzung von Deep-Learning-Aufgaben eine gute Unterstützung bieten. In diesem Artikel wird die Installation von PyTorch in PyCharm ausführlich vorgestellt und spezifische Codebeispiele bereitgestellt, um den Lesern den schnellen Einstieg in die Verwendung von PyTorch für Deep-Learning-Aufgaben zu erleichtern. Schritt 1: Installieren Sie PyCharm. Zuerst müssen wir sicherstellen, dass wir es haben
 Deep Learning mit PHP und PyTorch
Jun 19, 2023 pm 02:43 PM
Deep Learning mit PHP und PyTorch
Jun 19, 2023 pm 02:43 PM
Deep Learning ist ein wichtiger Zweig im Bereich der künstlichen Intelligenz und hat in den letzten Jahren immer mehr Aufmerksamkeit erhalten. Um Deep-Learning-Forschung und -Anwendungen durchführen zu können, ist es oft notwendig, einige Deep-Learning-Frameworks zu verwenden, um dies zu erreichen. In diesem Artikel stellen wir vor, wie man PHP und PyTorch für Deep Learning verwendet. 1. Was ist PyTorch? PyTorch ist ein von Facebook entwickeltes Open-Source-Framework für maschinelles Lernen. Es kann uns helfen, schnell Deep-Learning-Modelle zu erstellen und zu trainieren. PyTorc
 so schnell! Erkennen Sie Videosprache in nur wenigen Minuten mit weniger als 10 Codezeilen in Text
Feb 27, 2024 pm 01:55 PM
so schnell! Erkennen Sie Videosprache in nur wenigen Minuten mit weniger als 10 Codezeilen in Text
Feb 27, 2024 pm 01:55 PM
Hallo zusammen, ich bin Kite. Die Notwendigkeit, Audio- und Videodateien in Textinhalte umzuwandeln, war vor zwei Jahren schwierig, aber jetzt kann dies problemlos in nur wenigen Minuten gelöst werden. Es heißt, dass einige Unternehmen, um Trainingsdaten zu erhalten, Videos auf Kurzvideoplattformen wie Douyin und Kuaishou vollständig gecrawlt haben, dann den Ton aus den Videos extrahiert und sie in Textform umgewandelt haben, um sie als Trainingskorpus für Big-Data-Modelle zu verwenden . Wenn Sie eine Video- oder Audiodatei in Text konvertieren müssen, können Sie diese heute verfügbare Open-Source-Lösung ausprobieren. Sie können beispielsweise nach bestimmten Zeitpunkten suchen, zu denen Dialoge in Film- und Fernsehsendungen erscheinen. Kommen wir ohne weitere Umschweife zum Punkt. Whisper ist OpenAIs Open-Source-Whisper. Es ist natürlich in Python geschrieben und erfordert nur ein paar einfache Installationspakete.
 So installieren Sie Pytorch in PyCharm
Dec 08, 2023 pm 03:05 PM
So installieren Sie Pytorch in PyCharm
Dec 08, 2023 pm 03:05 PM
Installationsschritte: 1. Öffnen Sie PyCharm und erstellen Sie ein neues Python-Projekt. 2. Klicken Sie in der unteren Statusleiste von PyCharm auf das „Terminal“-Symbol, um das Terminalfenster zu öffnen. 3. Verwenden Sie im Terminalfenster den Befehl pip, um PyTorch zu installieren Je nach System und Anforderungen können Sie verschiedene Installationsmethoden auswählen. 4. Nach Abschluss der Installation können Sie Code in PyCharm schreiben und die PyTorch-Bibliothek importieren, um ihn zu verwenden.



