Enthüllte neue Version: Mathematische Prinzipien von Transformer, die Sie noch nie zuvor gesehen haben

Kürzlich wurde auf arxiv ein Artikel veröffentlicht, der eine neue Interpretation der mathematischen Prinzipien von Transformer bietet. Der Inhalt ist sehr lang und ich empfehle dringend, den Originalartikel zu lesen.

Im Jahr 2017 wurde „Attention is all you need“ von Vaswani et al. zu einem wichtigen Meilenstein in der Entwicklung der neuronalen Netzwerkarchitektur. Der Kernbeitrag dieses Artikels ist der Selbstaufmerksamkeitsmechanismus, die Innovation, die Transformers von traditionellen Architekturen unterscheidet und eine wichtige Rolle für seine hervorragende praktische Leistung spielt.

Tatsächlich ist diese Innovation zu einem wichtigen Katalysator für die Weiterentwicklung der künstlichen Intelligenz in Bereichen wie Computer Vision und Verarbeitung natürlicher Sprache geworden und spielt gleichzeitig eine Schlüsselrolle bei der Entstehung großer Sprachmodelle. Daher ist das Verständnis von Transformern und insbesondere der Mechanismen, mit denen die Selbstaufmerksamkeit Daten verarbeitet, ein entscheidender, aber weitgehend unerforschter Bereich.

Papieradresse: https://arxiv.org/pdf/2312.10794.pdf

Tiefe neuronale Netze (DNNs) haben ein gemeinsames Merkmal: Die Eingabedaten werden Schicht für Schicht der Reihe nach verarbeitet und bilden ein Zeit Diskretes dynamisches System (spezifische Inhalte finden Sie im vom MIT veröffentlichten „Deep Learning“, in China auch als „Flower Book“ bekannt). Diese Perspektive wurde erfolgreich verwendet, um Restnetzwerke auf zeitkontinuierlichen dynamischen Systemen zu modellieren, die als neuronale gewöhnliche Differentialgleichungen (neuronale ODEs) bezeichnet werden. 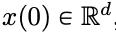In der Differentialgleichung der göttlichen Konstante entwickelt sich das Eingabebild entsprechend dem gegebenen zeitlich veränderlichen Geschwindigkeitsfeld 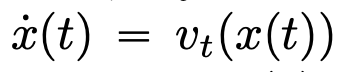über das Zeitintervall (0, T). 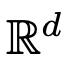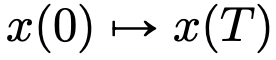Daher kann DNN als Flusskarte von einem zum anderen betrachtet werden. Selbst in Geschwindigkeitsfeldern 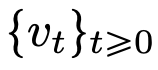besteht unter den Einschränkungen klassischer DNN-Architekturen eine starke Ähnlichkeit zwischen Flusskarten.

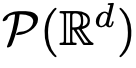Forscher fanden heraus, dass Transformer tatsächlich Flussabbildungen auf sind, also Abbildungen zwischen d-dimensionalen Wahrscheinlichkeitsmaßräumen (dem Raum der Wahrscheinlichkeitsmaße). Um diese Flusskartierung zu implementieren, die zwischen metrischen Räumen konvertiert, müssen Transformers ein mit mittlerem Feld interagierendes Partikelsystem einrichten.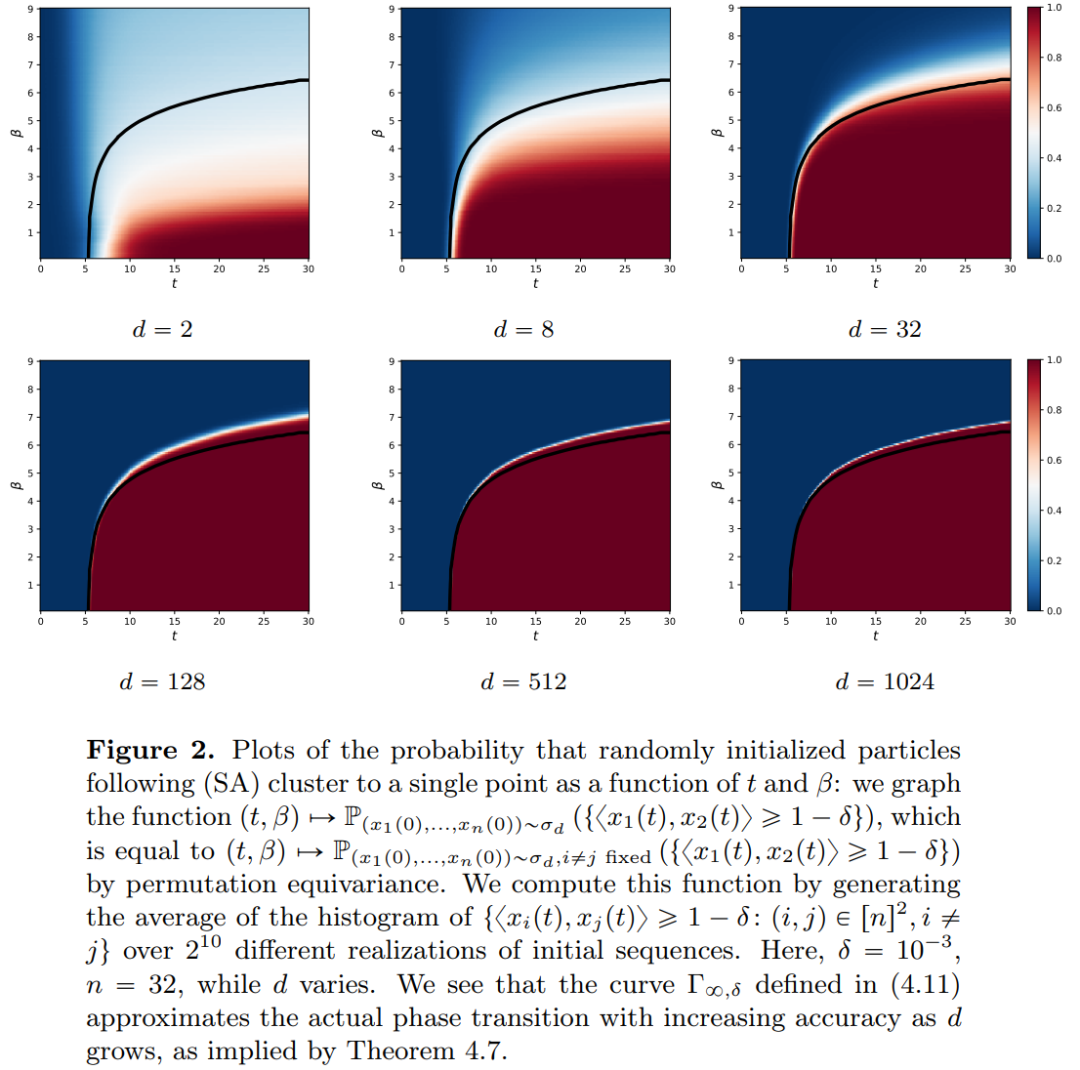

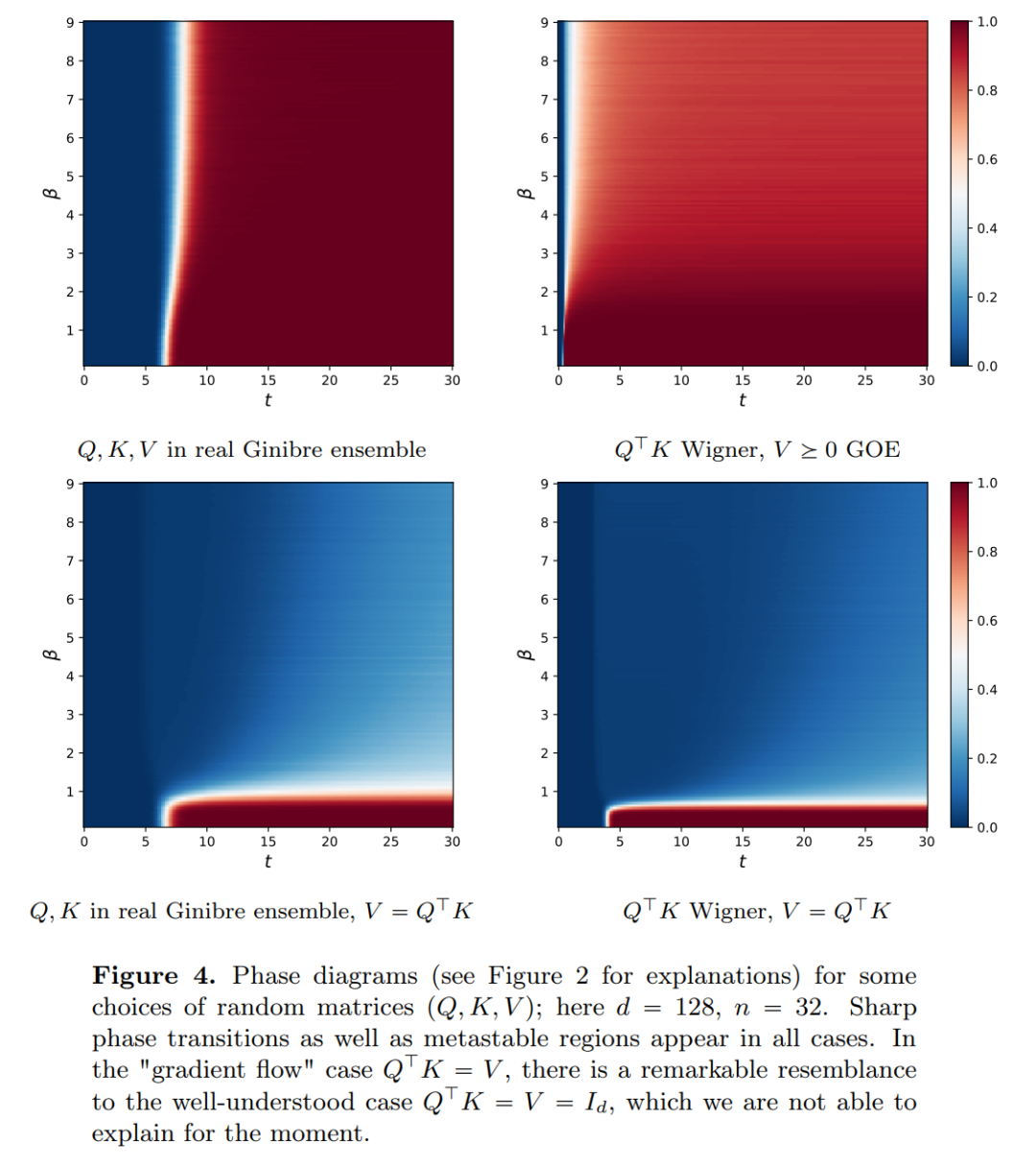
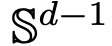Konkret folgt jedes Teilchen (das im Kontext von Deep Learning als Token verstanden werden kann) dem Fluss des Vektorfeldes, und der Fluss hängt vom empirischen Maß aller Teilchen ab. Die Gleichungen wiederum bestimmen die Entwicklung empirischer Partikelmessungen, ein Prozess, der lange dauern kann und anhaltende Aufmerksamkeit erfordert.

Die wichtigste Beobachtung der Forscher ist, dass Partikel dazu neigen, irgendwann zusammenzuklumpen. Dieses Phänomen zeigt sich besonders deutlich bei Lernaufgaben wie der einseitigen Ableitung (d. h. der Vorhersage des nächsten Wortes in einer Sequenz). Die Ausgabemetrik kodiert die Wahrscheinlichkeitsverteilung des nächsten Tokens und eine kleine Anzahl möglicher Ergebnisse kann basierend auf den Clustering-Ergebnissen herausgefiltert werden.

Die Forschungsergebnisse dieses Artikels zeigen, dass die Grenzverteilung tatsächlich eine Punktmasse ist und es keine Diversität oder Zufälligkeit gibt, dies steht jedoch nicht im Einklang mit den tatsächlichen Beobachtungsergebnissen. Dieses scheinbare Paradox wird durch die Tatsache gelöst, dass die Teilchen über lange Zeiträume in variablen Zuständen existieren. Wie aus den Abbildungen 2 und 4 ersichtlich ist, haben Transformatoren zwei unterschiedliche Zeitskalen: In der ersten Stufe bilden alle Token schnell mehrere Cluster, während sie in der zweiten Stufe (viel langsamer als die erste Stufe) durch den paarweisen Zusammenführungsprozess erfolgen In Clustern fallen alle Token schließlich an einem Punkt zusammen.

Das Ziel dieses Artikels ist zweifach. Einerseits soll Dieser Artikel einen allgemeinen und leicht verständlichen Rahmen für das Studium von Transformern aus mathematischer Sicht bieten. Insbesondere die Struktur dieser Systeme interagierender Teilchen ermöglicht es Forschern, konkrete Verbindungen zu etablierten Themen der Mathematik herzustellen, darunter nichtlineare Transportgleichungen, Wasserstein-Gradientenflüsse, Modelle kollektiven Verhaltens und optimale Konfigurationen von Punkten auf einer Kugel. Andererseits beschreibt dieser Artikel mehrere vielversprechende Forschungsrichtungen, mit besonderem Fokus auf Clustering-Phänomene über lange Zeiträume. Die von den Forschern vorgeschlagenen Hauptergebnismaße sind neu und werfen in der gesamten Arbeit auch offene Fragen auf, die sie für interessant halten.

Die Hauptbeiträge dieses Artikels sind in drei Teile gegliedert.

Teil 1: Modellieren. Dieser Artikel definiert ein ideales Modell der Transformer-Architektur, das die Anzahl der Schichten als kontinuierliche Zeitvariable behandelt. Dieser Abstraktionsansatz ist nicht neu und ähnelt dem Ansatz klassischer Architekturen wie ResNets. Das Modell dieses Artikels konzentriert sich nur auf zwei Schlüsselkomponenten der Transformer-Architektur: Selbstaufmerksamkeitsmechanismus und Ebenennormalisierung. Durch die Schichtnormalisierung werden Partikel effektiv auf den Raum der Einheitskugel beschränkt , während der Selbstaufmerksamkeitsmechanismus durch empirische Messungen eine nichtlineare Kopplung zwischen Partikeln erreicht. Das empirische Maß wiederum entwickelt sich gemäß einer Kontinuitäts-Partialdifferentialgleichung. In diesem Artikel wird auch ein einfacheres und benutzerfreundlicheres alternatives Modell für die Selbstaufmerksamkeit vorgestellt, ein Wasserstein-Gradientenfluss einer Energiefunktion. Es gibt bereits ausgereifte Forschungsmethoden für die optimale Konfiguration von Punkten auf der Sphäre der Energiefunktion.

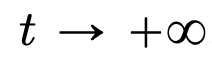Teil 2: Clustering. In diesem Teil schlagen die Forscher neue mathematische Ergebnisse zum Token-Clustering über einen längeren Zeitraum vor. Wie Satz 4.1 zeigt, sammelt sich im hochdimensionalen Raum eine Gruppe von n Teilchen, die zufällig auf der Einheitskugel initialisiert werden, an einem Punkt bei . Die genaue Beschreibung der Schrumpfungsrate der Partikelcluster durch die Forscher ergänzt dieses Ergebnis. Konkret zeichneten die Forscher Histogramme der Abstände zwischen allen Partikeln sowie der Zeitpunkte auf, zu denen alle Partikel kurz vor der vollständigen Clusterbildung standen (siehe Abschnitt 4 des Originalartikels). Die Forscher erzielten auch Clustering-Ergebnisse, ohne eine große Dimension d anzunehmen (siehe Abschnitt 5 des Originalartikels).

Teil 3: Der Blick nach vorne. In diesem Artikel werden mögliche zukünftige Forschungsrichtungen vorgeschlagen, indem Fragen vor allem in Form offener Fragen gestellt und durch numerische Beobachtungen untermauert werden. Die Forscher konzentrieren sich zunächst auf den Fall der Dimension d = 2 (siehe Abschnitt 6 des Originalartikels) und stellen den Zusammenhang mit dem Kuramoto-Oszillator her. Anschließend wird kurz gezeigt, wie schwierige Probleme im Zusammenhang mit der sphärischen Optimierung durch einfache und natürliche Änderungen am Modell gelöst werden können (siehe Abschnitt 7 des Originalartikels). In den folgenden Kapiteln werden die interagierenden Partikelsysteme untersucht, die es ermöglichen, Parameter in der Transformer-Architektur anzupassen, was später zu praktischen Anwendungen führen kann.

Das obige ist der detaillierte Inhalt vonEnthüllte neue Version: Mathematische Prinzipien von Transformer, die Sie noch nie zuvor gesehen haben. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!