Entdecken Sie die Bedeutung der perfekten Quadratformel

Was bedeutet die perfekte Quadratformel? Originalverleger: Zhang Yan
Klasse |. Thema „Perfekte Quadrate“ |
Unterrichtsmedien|Multimedia|
Lehrziele: Wissen und Fähigkeiten 1. Durch den Prozess der Erforschung der perfekten Quadratformel können die Schüler Forschungsmethoden vom Allgemeinen zum Spezifischen entwickeln und ihr Gespür für Symbole und ihre Argumentationsfähigkeiten weiterentwickeln. 2. In der Lage sein, die perfekte Quadratformel abzuleiten, die strukturellen Eigenschaften der Formel zu verstehen und die Formel zur Durchführung einfacher Berechnungen zu verwenden.
Prozess|Methode|Weitere Förderung der Fähigkeit der Schüler, Probleme mithilfe einer Kombination aus Zahlen und Formen zu lösen.|
Förderung des Interesses der Schüler an Mathematik, Verständnis für die Geschichte der Mathematik und Förderung der Innovationsfähigkeit.
Lehrschwerpunkt|Die Ableitung und Anwendung von (a±b)2=a2±2ab+b2.|
Lehrschwierigkeiten|Die Ableitung der perfekten Quadratformel, die strukturellen Eigenschaften der Formel und ihre Anwendung.|
Lehrprozessgestaltung|
Lehrverfahren und Lehrinhalte|Lehrer- und Schülerverhalten|Gestaltungsabsicht|
Erkunden und berechnen Sie die folgenden Gleichungen. |(1)(p+1)2 =(p+1)(p+1)=_________;|(2)(m+2)2=(m+2)(m+2)=_________;|( 3)(p-1)2 =(p-1)(p-1)=_________;|(4)(m-2)2=(m-2)(m-2)=_________ |Antwort: ( 1) p2+2p+1; (2)m2+4m+4; (4)m2-4m+4.|1 Berechnung: (a+b) 2 und (a-b) 2; und erklären Sie die entdeckten Regeln. |(a+b)2=(a+b)(a+b)= a(a+b)+b(a+b)=a2+ab+ab+b2|=a2+2ab+b2.ر| (a-b)2=(a-b)(a-b)=a(a-b)-b(a-b)=a2-ab-ab+b2=a2-2ab+b2.ر|2. Induktion der perfekten Quadratformel|Summe zweier Zahlen (oder Differenz) zum Quadrat, gleich der Summe ihrer Quadrate, addiere (oder subtrahiere) sie
Konzept der perfekten Quadratzahlen in der Mathematik
Perfekte quadratische Zahlen
(1) Eigenschaften perfekter Quadratzahlen
Wenn eine Zahl das perfekte Quadrat einer anderen ganzen Zahl ist, dann nennen wir diese Zahl eine perfekte quadratische Zahl, auch Quadratzahl genannt. Zum Beispiel:
0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441,484,…
Wenn Sie diese perfekten Quadratzahlen beobachten, können Sie ein Verständnis für die Regelmäßigkeit ihrer einzelnen Ziffern, Zehnerziffern, Summen usw. gewinnen. Schauen wir uns einige gemeinsame Eigenschaften perfekter Quadratzahlen an:
Eigenschaft 1: Die letzte Ziffer einer perfekten Quadratzahl kann nur 0,1,4,5,6,9 sein.
Eigenschaft 2: Die einzelne Ziffer des Quadrats einer ungeraden Zahl ist eine ungerade Zahl und die Zehnerstelle ist eine gerade Zahl.
Eigenschaft 3: Wenn die Zehnerstelle einer vollkommenen quadratischen Zahl eine ungerade Zahl ist, dann muss ihre Einerstelle 6 sein; wenn umgekehrt die Einerstelle einer vollkommenen quadratischen Zahl 6 ist, dann muss ihre Zehnerstelle eine ungerade Zahl sein.
Folge 1: Wenn die Zehnerstelle einer Zahl eine ungerade Zahl ist und die Einerstelle nicht 6 ist, dann darf die Zahl kein perfektes Quadrat sein.
Folge 2: Wenn die Einerstelle einer vollkommenen quadratischen Zahl nicht 6 ist, dann ist ihre Zehnerstelle eine gerade Zahl.
Eigenschaft 4: Das Quadrat einer geraden Zahl ist ein Vielfaches von 4; das Quadrat einer ungeraden Zahl ist ein Vielfaches von 4 plus 1.
Eigenschaft 5: Das Quadrat der ungeraden Zahlen ist vom Typ 8n+1; das Quadrat der geraden Zahlen ist vom Typ 8n oder 8n+4.
Eigenschaft 6: Die Form einer Quadratzahl muss eine der beiden folgenden sein: 3k, 3k+1.
Eigenschaft 7: Das Quadrat einer Zahl, die nicht durch 5 teilbar ist, ist vom Typ 5k±1, und das Quadrat einer Zahl, die durch 5 teilbar ist, ist vom Typ 5k.
Eigenschaft 8: Die Form einer Quadratzahl hat eine der folgenden Formen: 16m, 16m+1, 16m+4, 16m+9.
Das obige ist der detaillierte Inhalt vonEntdecken Sie die Bedeutung der perfekten Quadratformel. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Wie bearbeite ich die Registrierung? (WARNUNG: Verwenden Sie mit Vorsicht!)
Mar 21, 2025 pm 07:46 PM
Wie bearbeite ich die Registrierung? (WARNUNG: Verwenden Sie mit Vorsicht!)
Mar 21, 2025 pm 07:46 PM
In Artikel werden die Bearbeitungs -Windows -Registrierung, Vorsichtsmaßnahmen, Sicherungsmethoden und potenzielle Probleme aus falschen Änderungen erläutert. Hauptproblem: Risiken der Systeminstabilität und des Datenverlusts durch unsachgemäße Änderungen.
 Entdecken Sie, wie Sie die Antriebsgesundheitswarnung in Windows -Einstellungen beheben können
Mar 19, 2025 am 11:10 AM
Entdecken Sie, wie Sie die Antriebsgesundheitswarnung in Windows -Einstellungen beheben können
Mar 19, 2025 am 11:10 AM
Was bedeutet die Drive Health -Warnung in Windows -Einstellungen und was sollten Sie tun, wenn Sie die Festplattenwarnung erhalten? Lesen Sie dieses Php.cn-Tutorial, um Schritt-für-Schritt-Anweisungen zu erhalten, um diese Situation zu bewältigen.
 Wie verwalte ich Dienste in Windows?
Mar 21, 2025 pm 07:52 PM
Wie verwalte ich Dienste in Windows?
Mar 21, 2025 pm 07:52 PM
In Artikel werden die Verwaltung von Windows -Diensten für die Systemgesundheit erörtert, einschließlich Starten, Stoppen, Neustarten von Diensten und Best Practices für Stabilität.
 Wie benutze ich den Gruppenrichtlinien -Editor (Gpedit.msc)?
Mar 21, 2025 pm 07:48 PM
Wie benutze ich den Gruppenrichtlinien -Editor (Gpedit.msc)?
Mar 21, 2025 pm 07:48 PM
In dem Artikel wird erläutert, wie der Gruppenrichtlinieneditor (Gpedit.MSC) in Windows verwendet wird, um die Systemeinstellungen zu verwalten, um gemeinsame Konfigurationen und Fehlerbehebungsmethoden hervorzuheben. Es stellt fest, dass gpedit.msc in Windows Home Editions nicht verfügbar ist, was schlägt, was vorschlägt, was vorschlägt
 Wie ändere ich die Standard -App für einen Dateityp?
Mar 21, 2025 pm 07:48 PM
Wie ändere ich die Standard -App für einen Dateityp?
Mar 21, 2025 pm 07:48 PM
In Artikeln werden Standard -Apps für Dateitypen unter Windows geändert, einschließlich Rückkehr- und Massenänderungen. Hauptproblem: Keine integrierte Option zur Änderung der Schüttung.
 Windows -Metadaten- und Internetdiensteprobleme: Wie beheben Sie es?
Apr 02, 2025 pm 03:57 PM
Windows -Metadaten- und Internetdiensteprobleme: Wie beheben Sie es?
Apr 02, 2025 pm 03:57 PM
Möglicherweise sehen Sie, dass die „Verbindung zu den Windows Metadata und Internet Services (WMIS) nicht hergestellt werden konnte“. Fehler beim Ereigniszuschauer. In diesem Beitrag von PHP.CN wird das Problem der Windows -Metadaten und des Internet -Dienste entfernen.
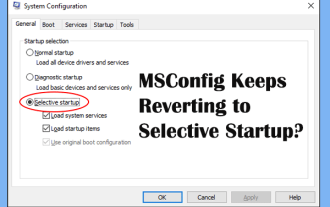 MSConfig kehrt immer wieder zum selektiven Startup zurück? 2 Lösungen hier
Mar 28, 2025 pm 12:06 PM
MSConfig kehrt immer wieder zum selektiven Startup zurück? 2 Lösungen hier
Mar 28, 2025 pm 12:06 PM
Sind Sie zu einem Problem befragt, das MSConfig immer wieder zum selektiven Start in Ihren Fenstern zurückkehrt? Wie wechsle ich zum normalen Start, wenn Sie es benötigen? Probieren Sie die in diesem Php.cn -Post erläuterten Methoden aus, um einen zu finden, der für Sie funktioniert.
 So beheben Sie das KB5035942 -Update -Probleme - Absturzsystem
Apr 02, 2025 pm 04:16 PM
So beheben Sie das KB5035942 -Update -Probleme - Absturzsystem
Apr 02, 2025 pm 04:16 PM
KB5035942 Update -Probleme - Das Absturzsystem kommt häufig bei Benutzern vor. Die Menschen hoffen, einen Ausweg aus der Art von Schwierigkeiten herauszuholen, wie zum Beispiel eines Absturzsystems, Installation oder Klangprobleme. Targeting dieser Situationen, in diesem Beitrag, der von Php.cn Wil veröffentlicht wurde




