 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Durchbrechen Sie die Informationsbarriere! Schockierendes großformatiges 3D-Visualisierungstool wird veröffentlicht!
Durchbrechen Sie die Informationsbarriere! Schockierendes großformatiges 3D-Visualisierungstool wird veröffentlicht!
Durchbrechen Sie die Informationsbarriere! Schockierendes großformatiges 3D-Visualisierungstool wird veröffentlicht!
Kürzlich hat ein Neuseeländer, Brendan Bycroft, in der Technologiebranche für Aufsehen gesorgt. Ein von ihm ins Leben gerufenes Projekt mit dem Namen „Large Model 3D Visualization“ stand nicht nur ganz oben auf der Liste der Hacker News, sondern seine schockierende Wirkung ist sogar noch umwerfender. Durch dieses Projekt werden Sie in nur wenigen Sekunden vollständig verstehen, wie LLM (Large Language Model) funktioniert.
Ob Sie ein Technologie-Enthusiast sind oder nicht, dieses Projekt wird Ihnen ein beispielloses visuelles Fest und kognitive Erleuchtung bescheren. Lassen Sie uns gemeinsam diese atemberaubende Kreation erkunden!
Einführung
In diesem Projekt analysierte Bycroft im Detail ein leichtes GPT-Modell namens Nano-GPT, das vom OpenAI-Wissenschaftler Andrej Karpathy entwickelt wurde. Als reduzierte Version des GPT-Modells verfügt das Modell nur über 85.000 Parameter. Obwohl dieses Modell viel kleiner ist als GPT-3 oder GPT-4 von OpenAI, kann man natürlich sagen, dass „ein Spatz klein ist, aber alle inneren Organe hat“.
Nano-GPT GitHub: https://github.com/karpathy/nanoGPT
Um die Demonstration jeder Schicht des Transformer-Modells zu erleichtern, hat Bycroft eine sehr einfache Zielaufgabe für das Nano-GPT-Modell arrangiert: das Modell Die Eingabe besteht aus 6 Buchstaben „CBABBC“, die Ausgabe ist eine in alphabetischer Reihenfolge angeordnete Folge, zum Beispiel die Ausgabe „ABBBCC“.
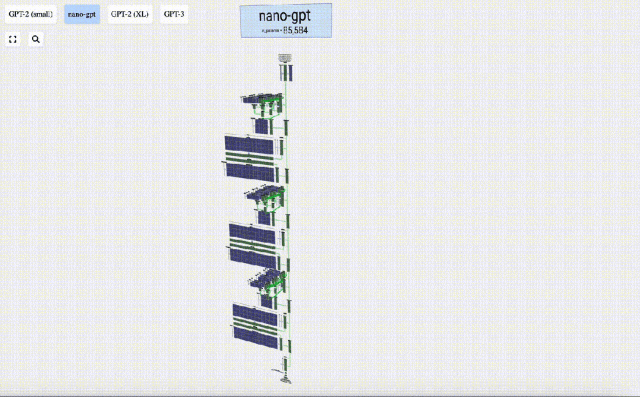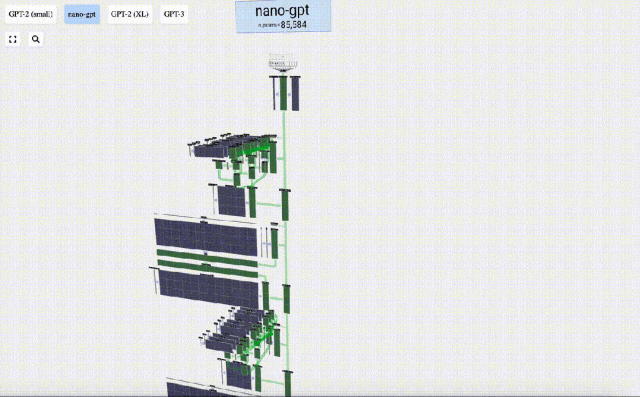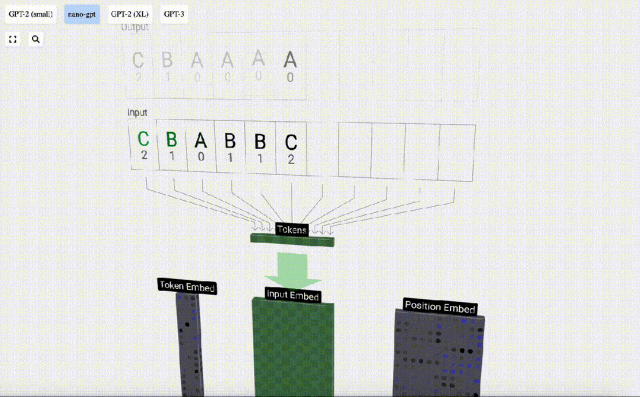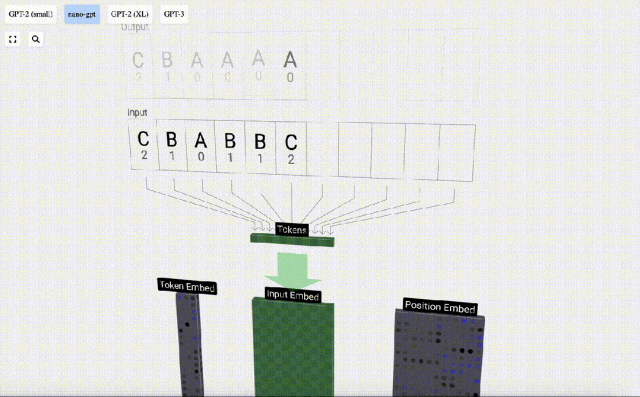
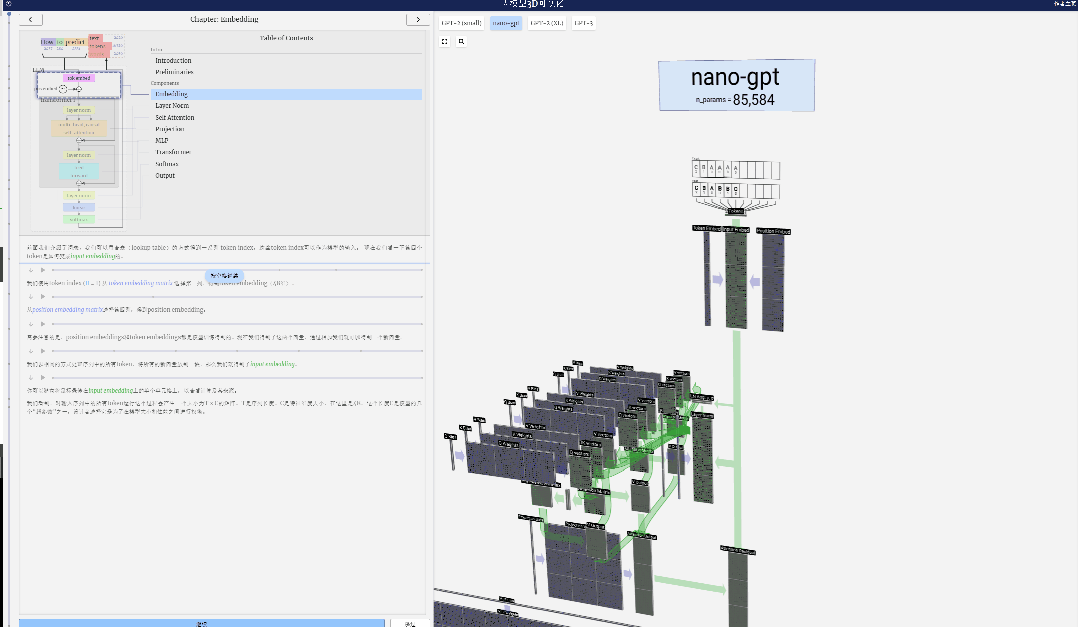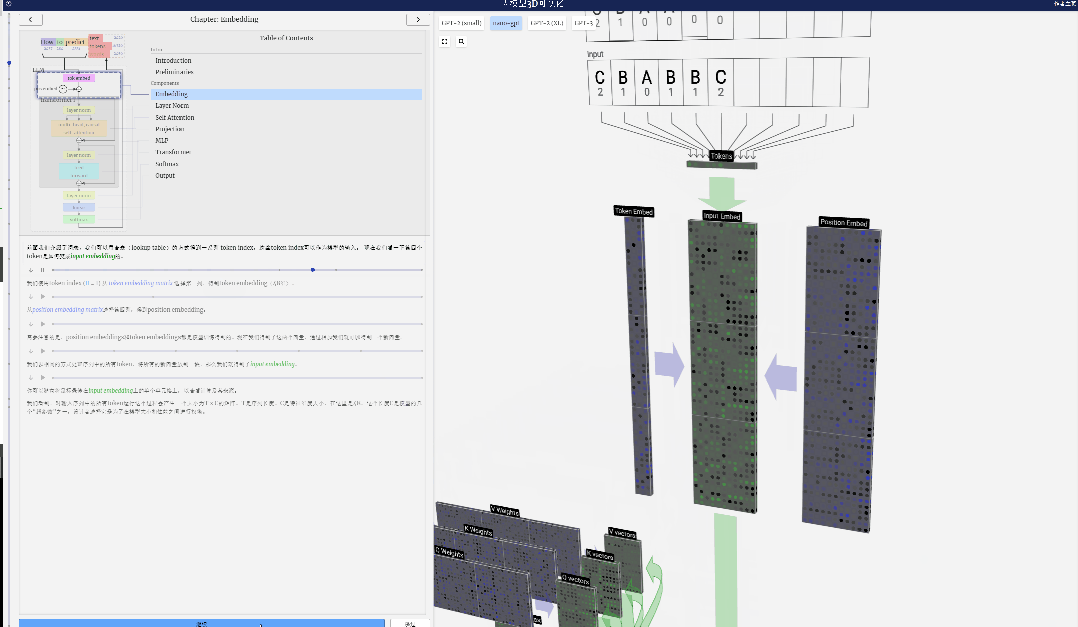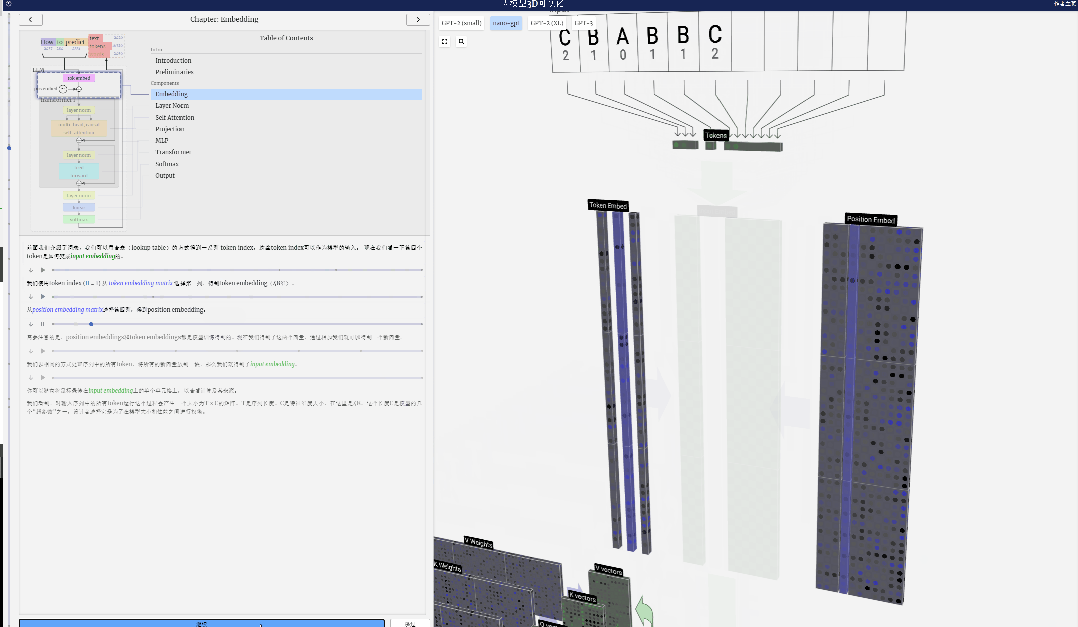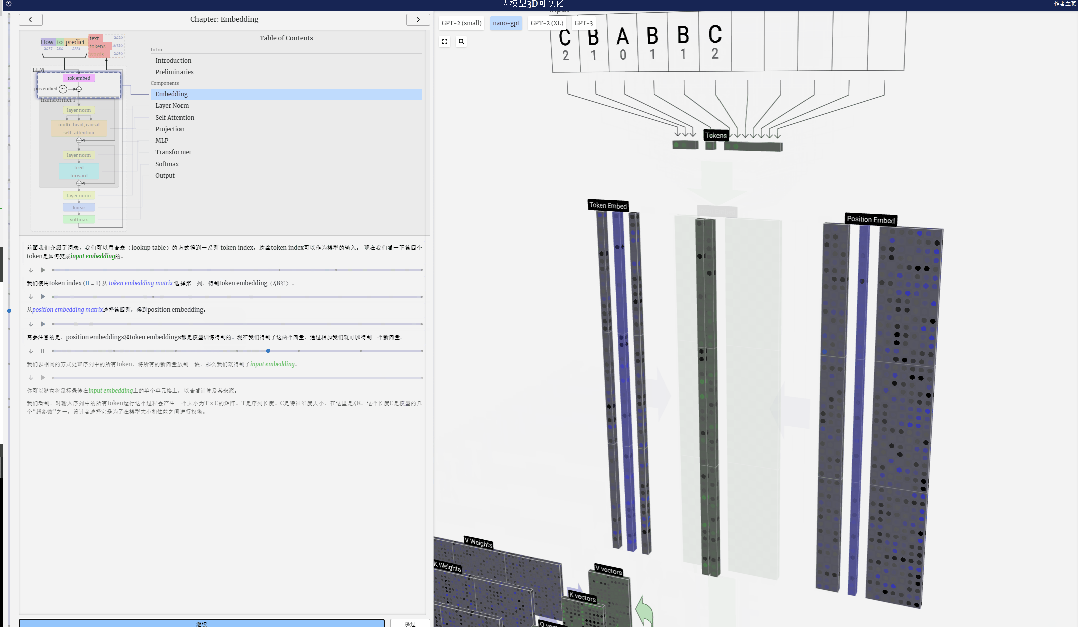
Wir nennen jeden Buchstaben ein Token, und diese verschiedenen Buchstaben bilden den Wortschatz:
Für diese Tabelle wird jedem Buchstaben ein tiefgestellter Token-Index zugewiesen. Die aus diesen Indizes zusammengesetzte Sequenz kann als Eingabe des Modells verwendet werden: 2 1 0 1 1 2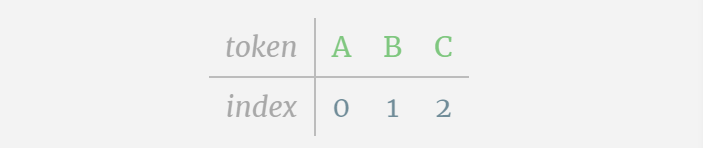
In der 3D-Visualisierung stellt jede grüne Zelle eine berechnete Zahl dar, während jede blaue Zelle das Gewicht des Modells darstellt . 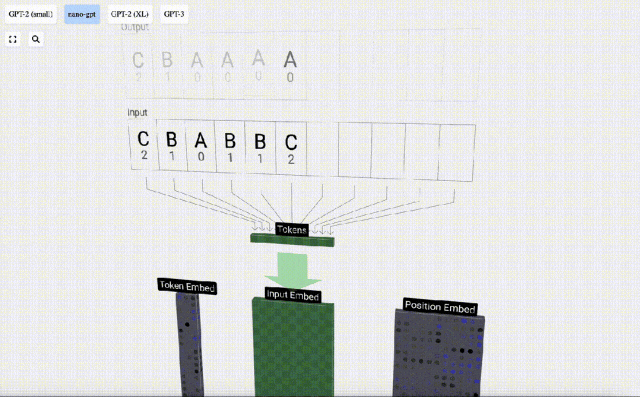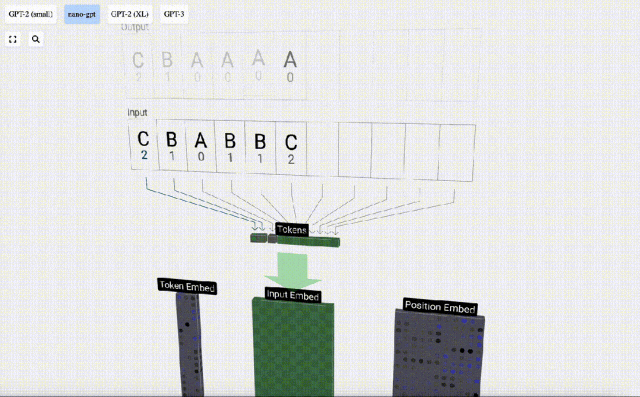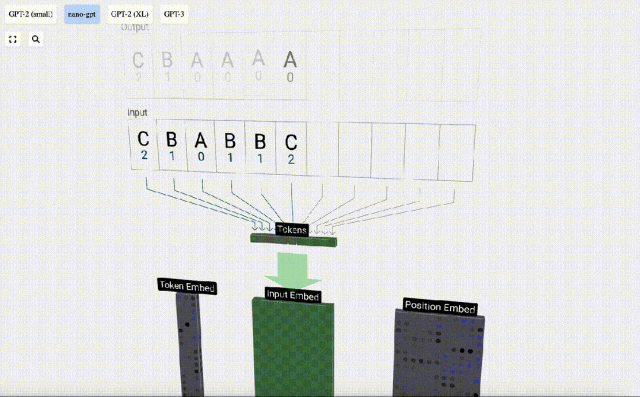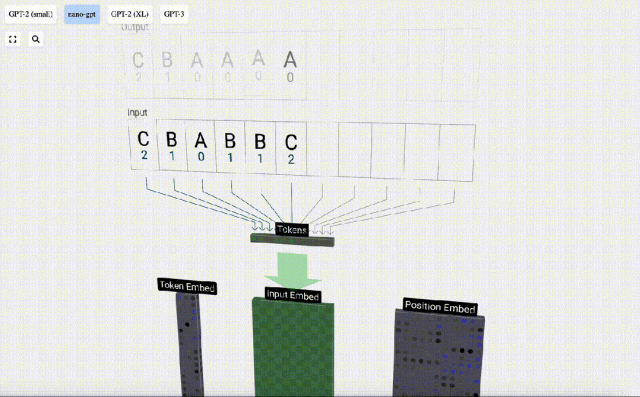
Bei der Sequenzverarbeitung wird jede Zahl zunächst in einen C-dimensionalen Vektor umgewandelt. Dieser Vorgang wird als Einbettung bezeichnet. Bei Nano-GPT beträgt die Dimension dieser Einbettung normalerweise 48 Dimensionen. Durch diesen Einbettungsvorgang wird jede Zahl als Vektor im C-dimensionalen Raum dargestellt, was eine bessere nachfolgende Verarbeitung und Analyse ermöglicht. 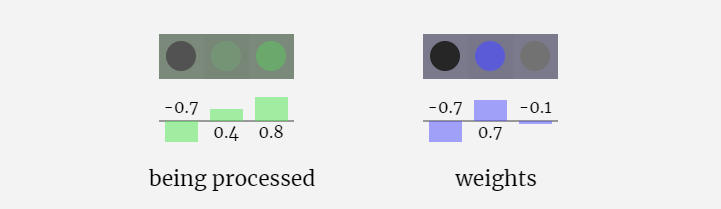
Einbettung wird über eine Reihe von Zwischenmodellschichten berechnet, die im Allgemeinen als Transformatoren bezeichnet werden, und erreicht schließlich die unterste Schicht. 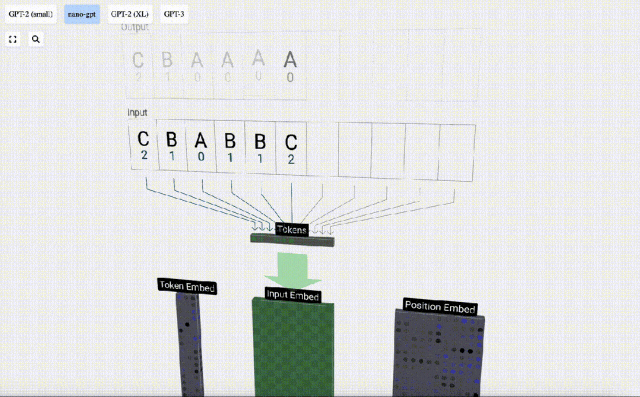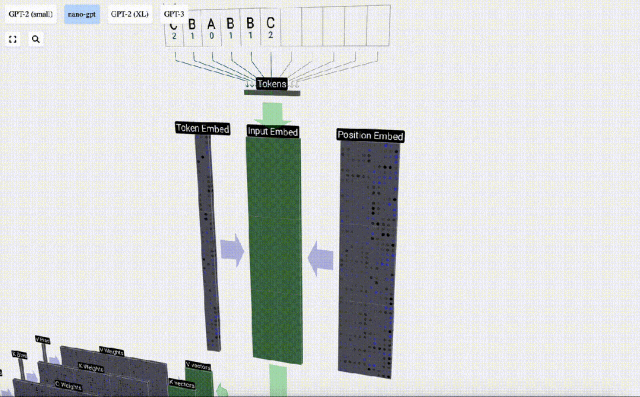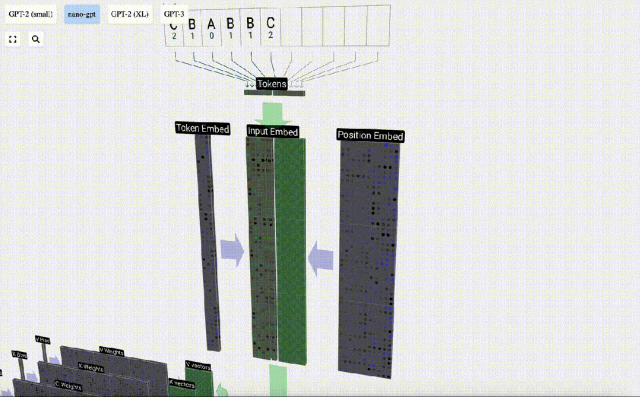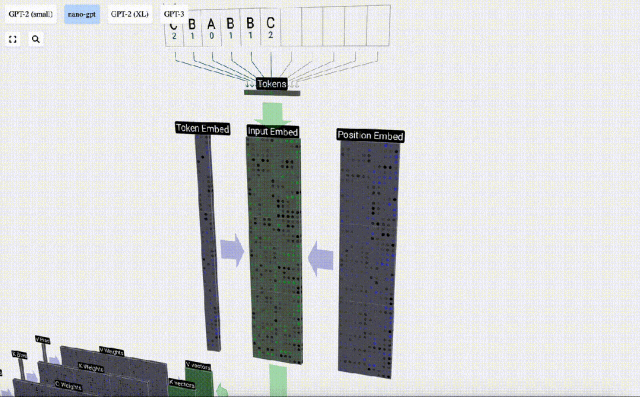
„Was ist also die Ausgabe?“
GPT-3 verfügt über 175 Milliarden Parameter und die Modellebene verfügt über 8 Spalten, die den gesamten Bildschirm dicht abdecken.
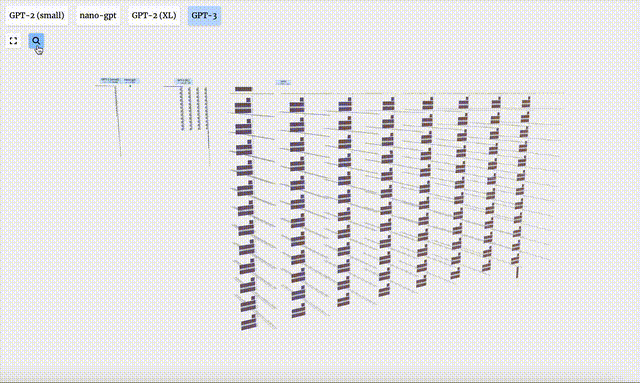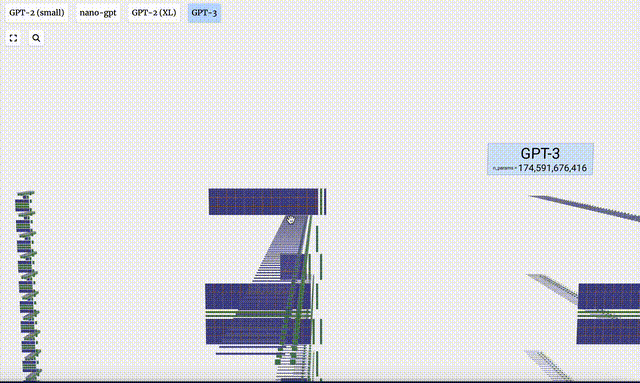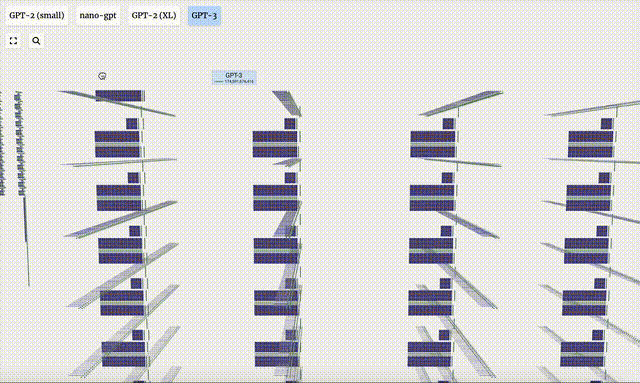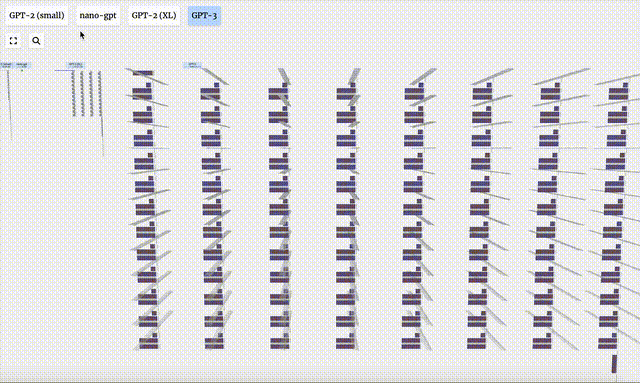 Verschiedene Parameterversionen des GPT-2-Modells weisen große architektonische Unterschiede auf. Hier nehmen wir als Beispiele die 15 Milliarden Parameter von GPT-2 (XL) und die 124 Millionen Parameter von GPT-2 (Small).
Verschiedene Parameterversionen des GPT-2-Modells weisen große architektonische Unterschiede auf. Hier nehmen wir als Beispiele die 15 Milliarden Parameter von GPT-2 (XL) und die 124 Millionen Parameter von GPT-2 (Small).

Es ist zu beachten, dass sich diese Visualisierung hauptsächlich auf die Modellinferenz (Inferenz) und nicht auf das Training konzentriert und daher nur einen kleinen Teil des gesamten maschinellen Lernprozesses darstellt. Darüber hinaus wird hier davon ausgegangen, dass die Gewichte des Modells vorab trainiert wurden, und dann wird die Modellinferenz verwendet, um eine Ausgabe zu generieren. 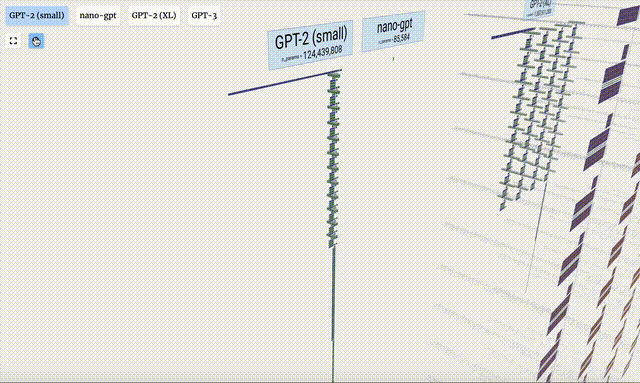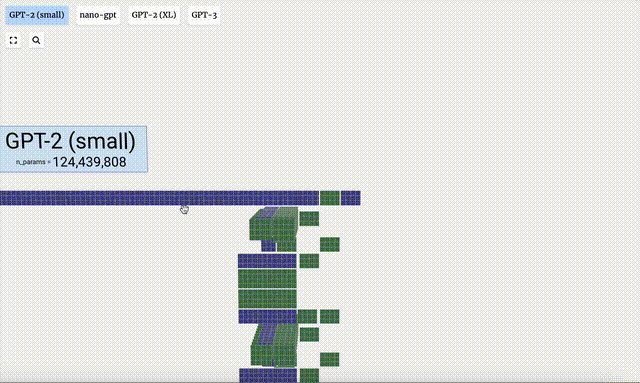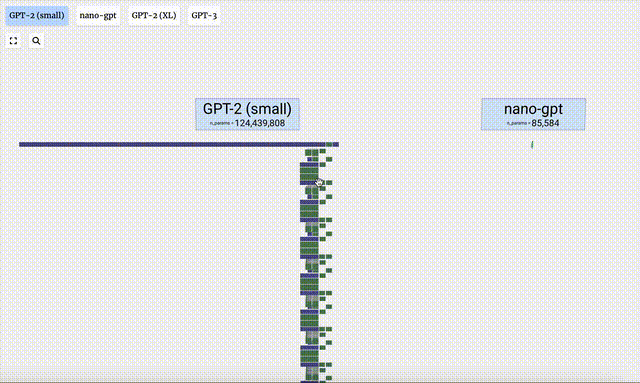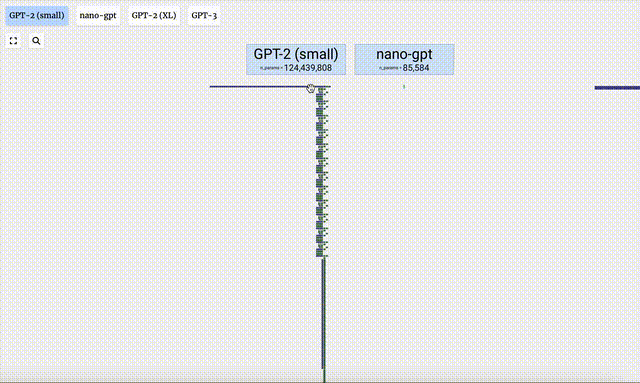
Diese Ganzzahlen, der Token-Index, sind das erste und einzige Mal, dass wir Ganzzahlen im Modell sehen. Danach werden Operationen mit Gleitkommazahlen (Dezimalzahlen) ausgeführt.
Nehmen Sie hier das 4. Token (Index 3) als Beispiel, um zu sehen, wie es zum Generieren des 4. Spaltenvektors der Eingabeeinbettung verwendet wird.

Verwenden Sie zunächst den Token-Index (hier wird B = 1 als Beispiel genommen), um die zweite Spalte aus der Token-Einbettungsmatrix auszuwählen und einen Spaltenvektor der Größe C = 48 (48 Dimensionen) zu erhalten, der aufgerufen wird Token-Einbettung.

Wählen Sie dann die vierte Spalte aus der Positionseinbettungsmatrix aus („Da wir uns hier hauptsächlich den (t = 3) Token B an der 4. Position ansehen“), erhalten wir auf ähnliche Weise eine Größe von C=48 (48 Dimensionen) Spaltenvektor, sogenannte Positionseinbettung.

Es ist zu beachten, dass Positionseinbettungen und Tokeneinbettungen beide durch Modelltraining erhalten werden (blau gekennzeichnet). Da wir nun diese beiden Vektoren haben, können wir durch Addition einen neuen Spaltenvektor der Größe C=48 erhalten.

Verarbeiten Sie als Nächstes alle Token in der Reihenfolge im selben Prozess und erstellen Sie einen Satz von Vektoren, die die Token-Werte und ihre Positionen enthalten.

Wie aus der obigen Abbildung ersichtlich ist, führt die Ausführung dieses Prozesses für alle Token in der Eingabesequenz zu einer Matrix der Größe TxC. Unter diesen repräsentiert T die Sequenzlänge. C steht für Kanal, wird aber auch Feature oder Dimension oder Einbettungsgröße genannt, die in diesem Fall 48 beträgt. Diese Länge C ist einer von mehreren „Hyperparametern“ des Modells, die vom Designer ausgewählt wurden, um einen Kompromiss zwischen Modellgröße und Leistung zu erzielen.
Diese Matrix mit der Dimension TxC ist die Eingabeeinbettung und wird durch das Modell weitergegeben.
Kleiner Tipp: Fahren Sie gerne mit der Maus über eine einzelne Zelle in der Eingabeeinbettung, um die Berechnung und ihre Quelle anzuzeigen.
Schichtnorm
Die zuvor erhaltene Eingabe-Einbettungsmatrix ist die Eingabe der Transformer-Schicht.
Der erste Schritt der Transformer-Ebene besteht darin, eine Ebenennormalisierung für die Eingabeeinbettungsmatrix durchzuführen. Dies ist eine Operation zum Normalisieren der Werte jeder Spalte der Eingabematrix.
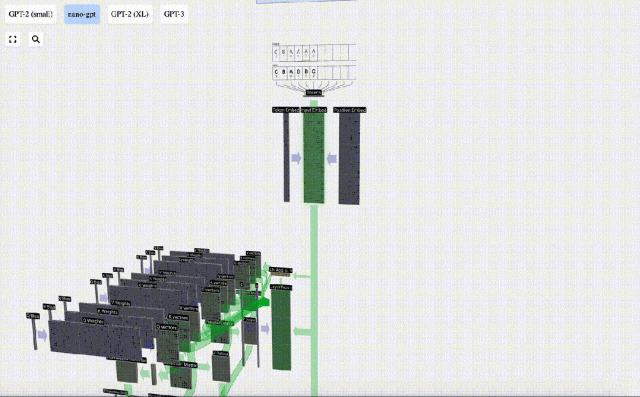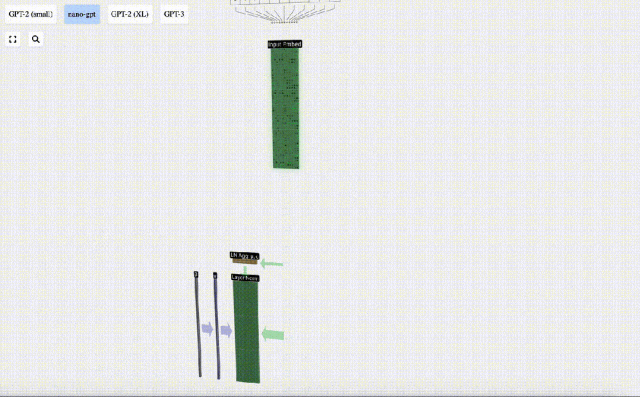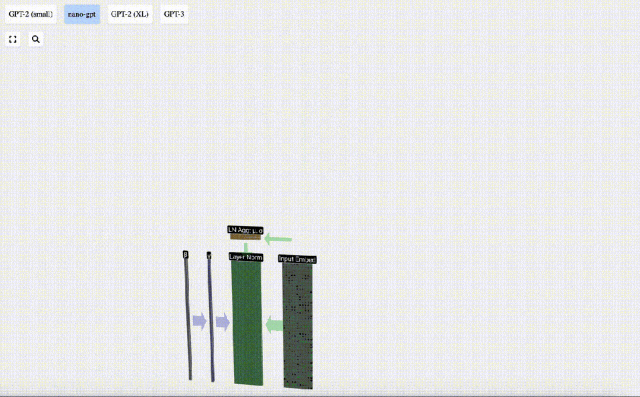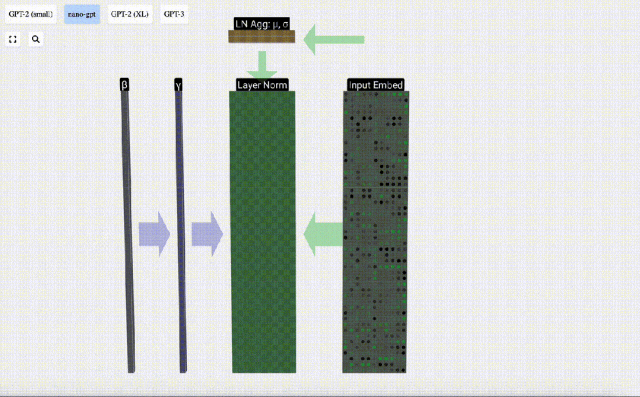
Normalisierung ist ein wichtiger Schritt beim Training tiefer neuronaler Netze, der dazu beiträgt, die Stabilität des Modells während des Trainingsprozesses zu verbessern.
Wir können die Spalten der Matrix separat betrachten. Die vierte Spalte dient unten als Beispiel.
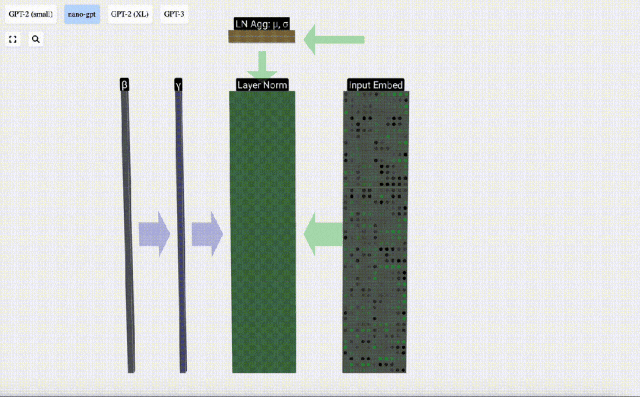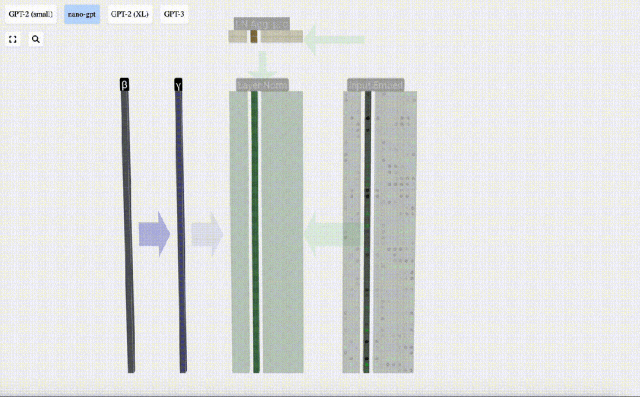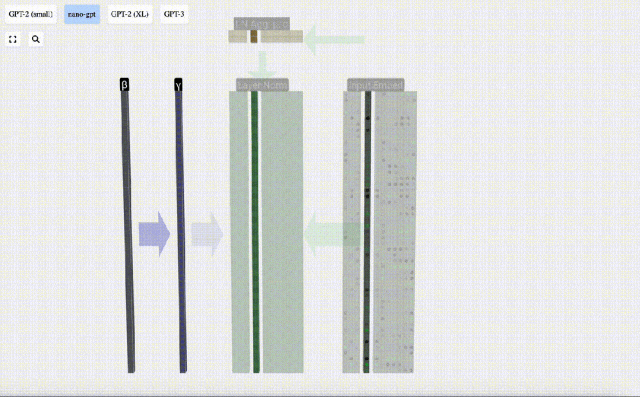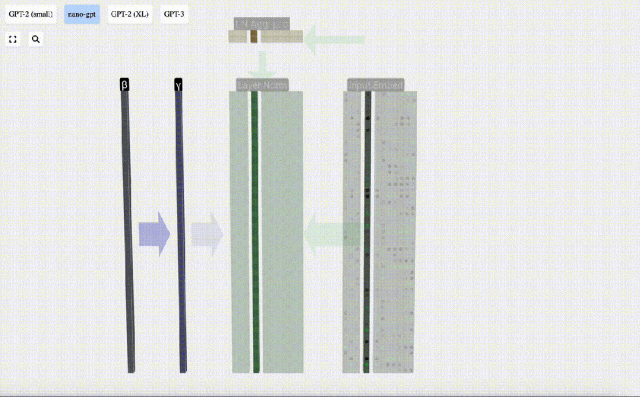
Das Ziel der Normalisierung besteht darin, dass der Wert jeder Spalte einen Mittelwert von 0 und eine Standardabweichung von 1 aufweist. Um dies zu erreichen, berechnen Sie den Mittelwert und die Standardabweichung jeder Spalte, subtrahieren dann den entsprechenden Mittelwert und dividieren durch die entsprechende Standardabweichung für jede Spalte.
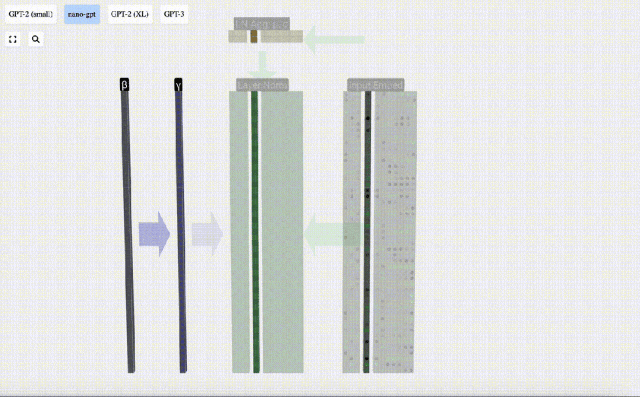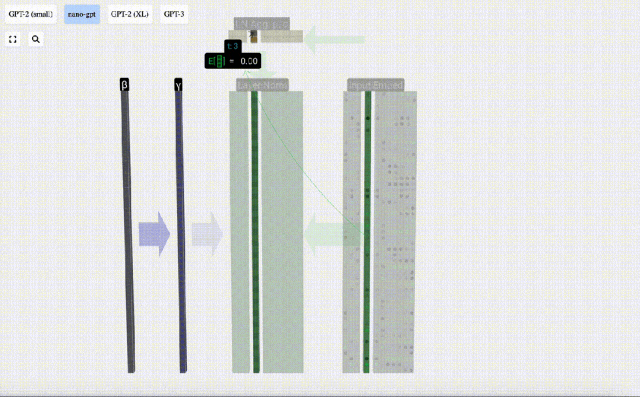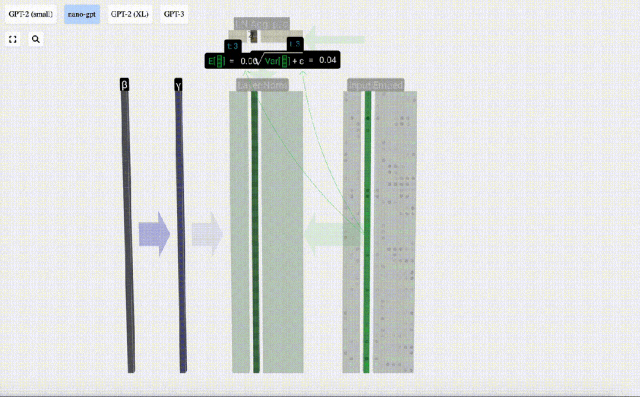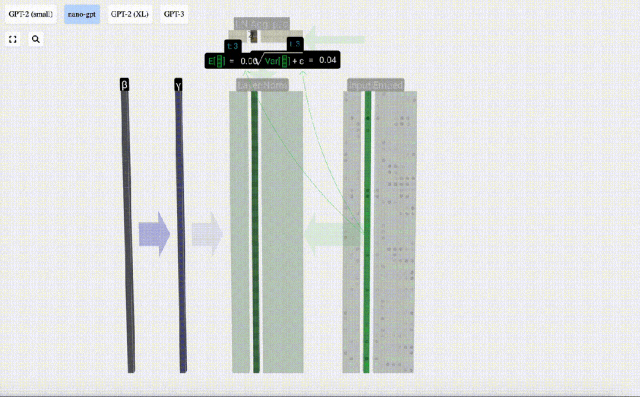
Hier wird E[x] verwendet, um den Mittelwert darzustellen, und Var[x] wird verwendet, um die Varianz (das Quadrat der Standardabweichung) darzustellen. epsilon(ε = 1×10^-5) soll Fehler bei der Division durch 0 verhindern.
Berechnen und speichern Sie das normalisierte Ergebnis, multiplizieren Sie es dann mit dem Lerngewichtsgewicht (γ) und addieren Sie den Bias Bias (β), um das endgültige normalisierte Ergebnis zu erhalten.
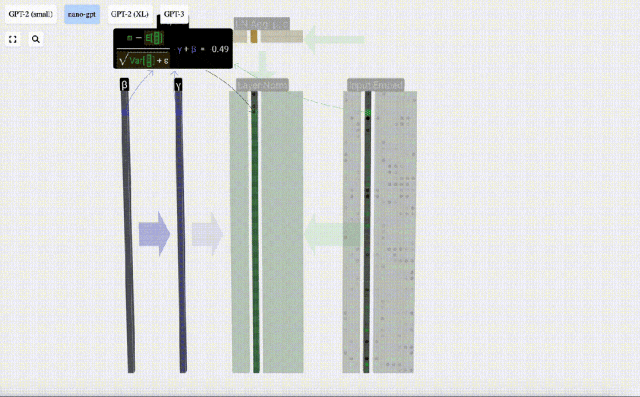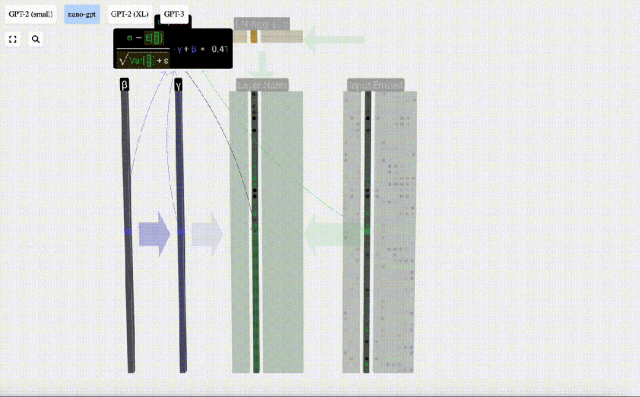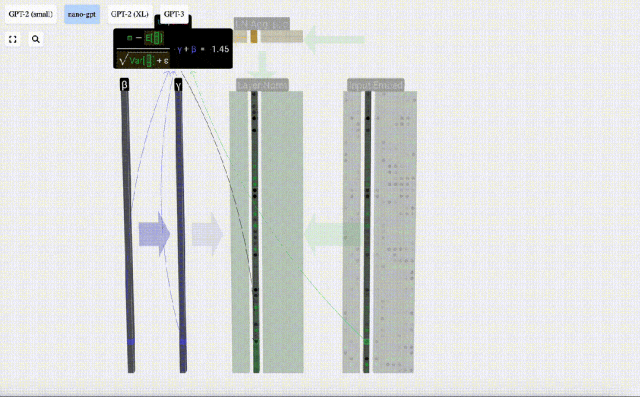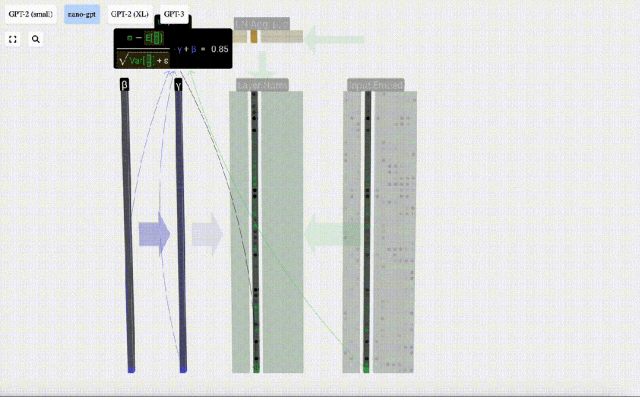
Führen Sie abschließend eine Normalisierungsoperation für jede Spalte der Eingabeeinbettungsmatrix durch, um die normalisierte Eingabeeinbettung zu erhalten, und übergeben Sie sie an die Selbstaufmerksamkeitsschicht (Selbstaufmerksamkeit).
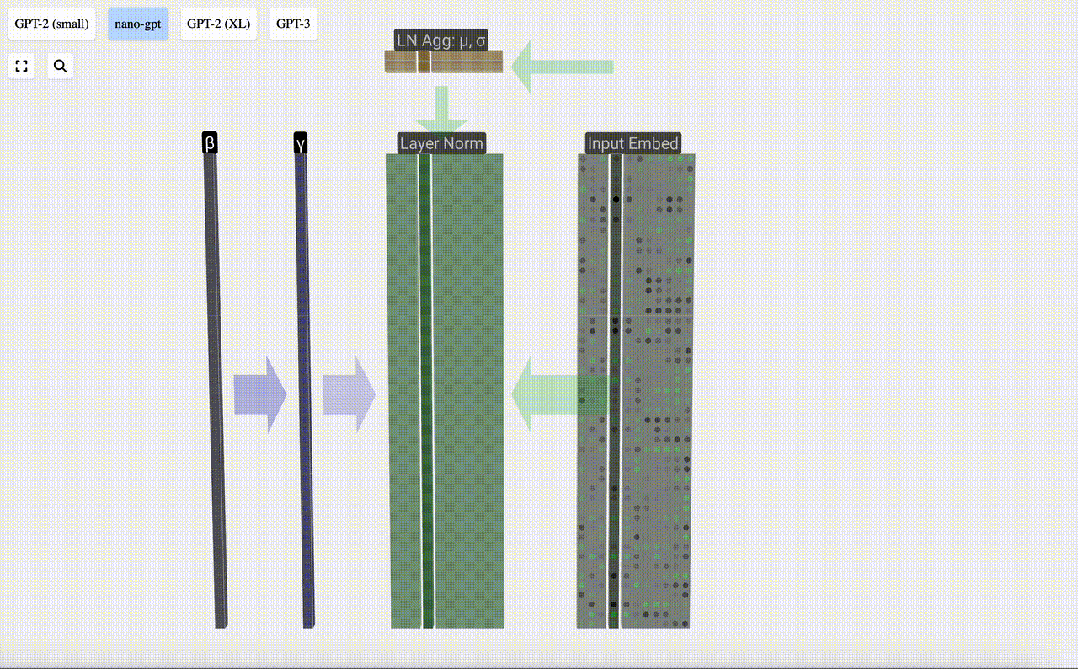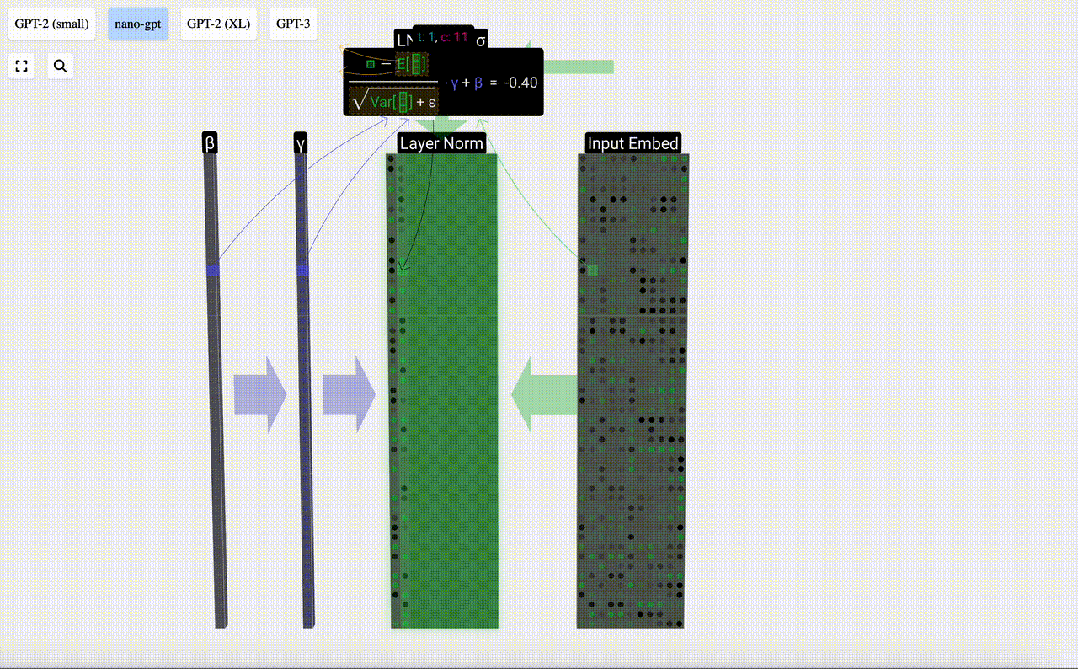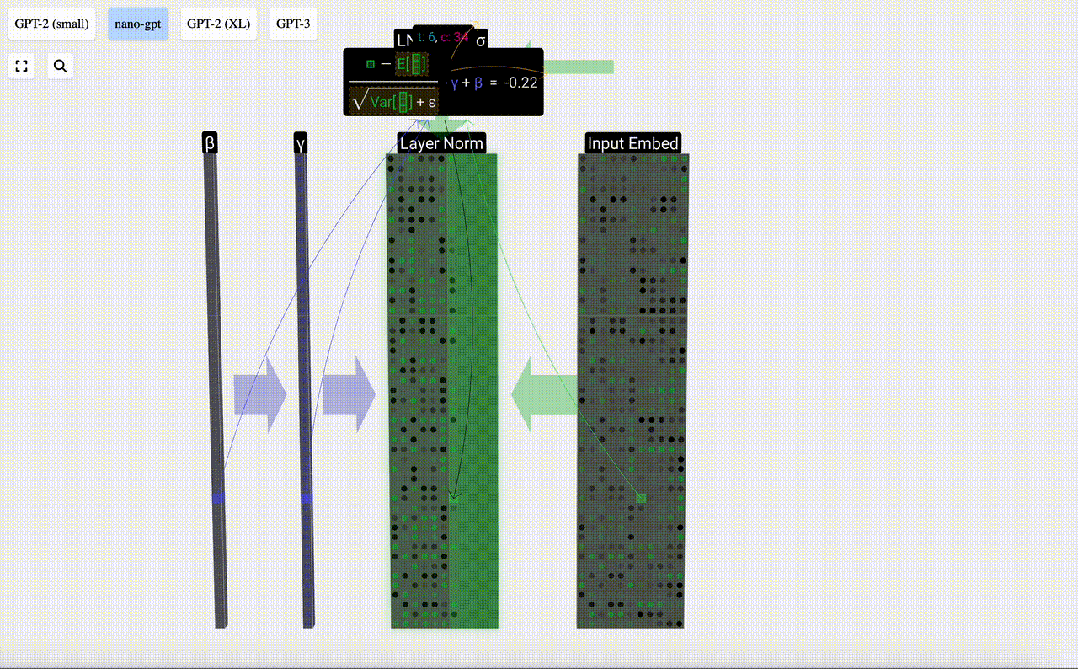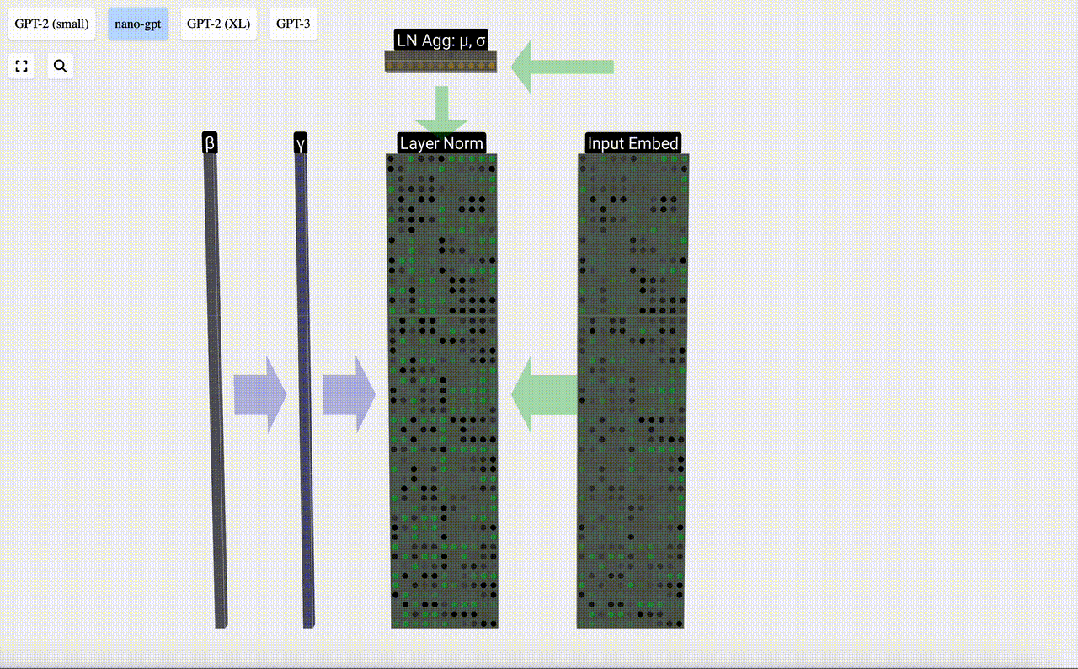
Selbstaufmerksamkeit
Die Selbstaufmerksamkeitsschicht ist wahrscheinlich der Kernbestandteil des Transformers. In dieser Phase können die Spalten in der Eingabeeinbettung miteinander „kommunizieren“, während in anderen Phasen jede Spalte unabhängig existiert.
Die Selbstaufmerksamkeitsebene besteht aus mehreren Selbstaufmerksamkeitsköpfen. In diesem Beispiel gibt es drei Selbstaufmerksamkeitsköpfe. Die Eingabe jedes Headers macht 1/3 der Eingabeeinbettung aus, und wir konzentrieren uns jetzt nur auf einen davon.

Der erste Schritt besteht darin, aus Spalte C der normalisierten Eingabeeinbettungsmatrix drei Vektoren für jede Spalte zu generieren. Diese sind QKV:
- Q: Abfragevektor
- K: Schlüsselvektor Schlüsselvektor
- V: Wert Vektor Wertvektor
Um diese Vektoren zu erzeugen, wird eine Matrix-Vektor-Multiplikation plus eine Vorspannung verwendet. Jede Ausgabeeinheit ist eine lineare Kombination von Eingabevektoren.
Zum Beispiel wird der Abfragevektor durch die Skalarproduktoperation zwischen einer Zeile der Q-Gewichtsmatrix und einer Spalte der Eingabematrix vervollständigt.
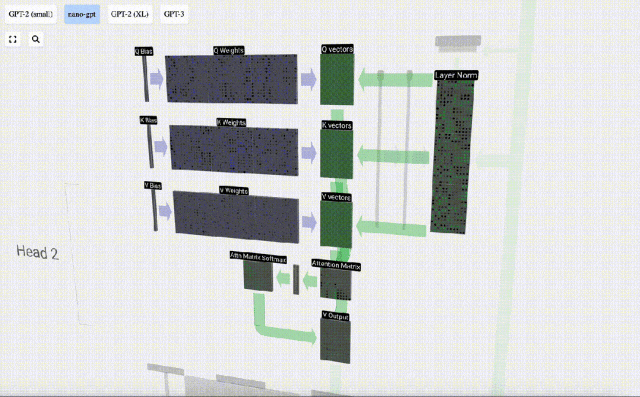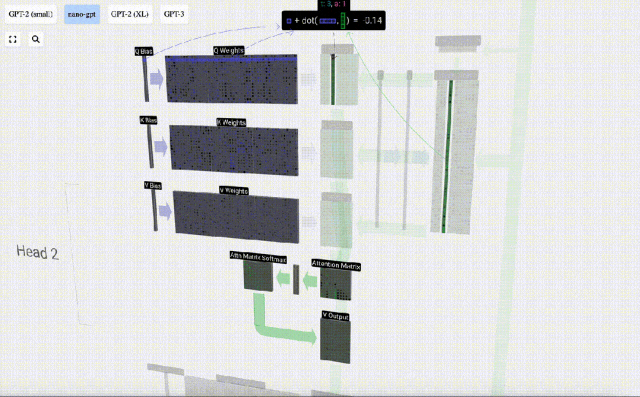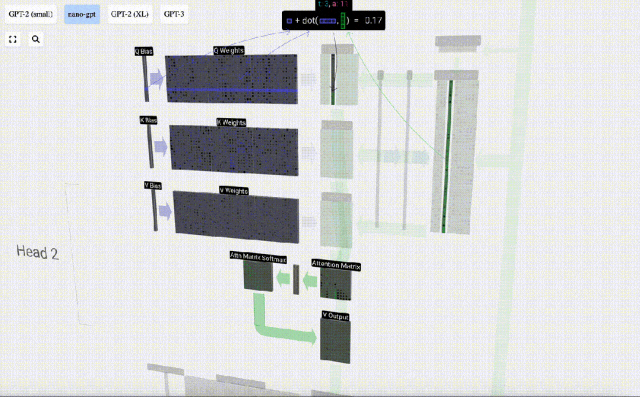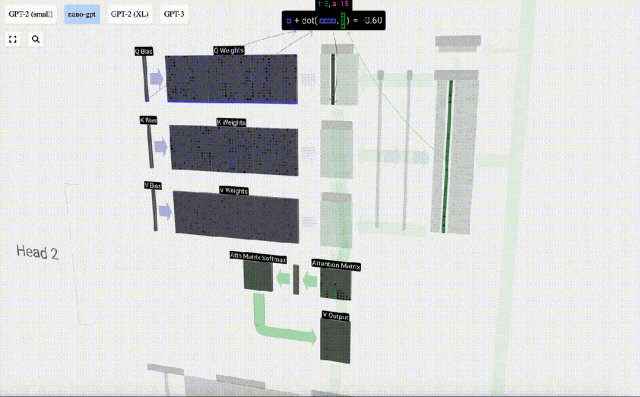
Die Funktionsweise des Skalarprodukts ist sehr einfach: Multiplizieren Sie einfach die entsprechenden Elemente und addieren Sie sie dann.
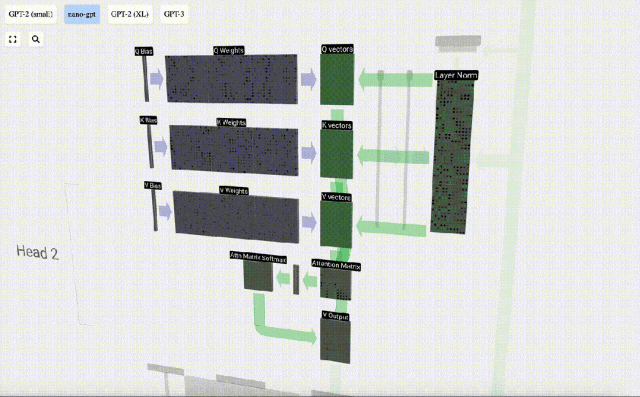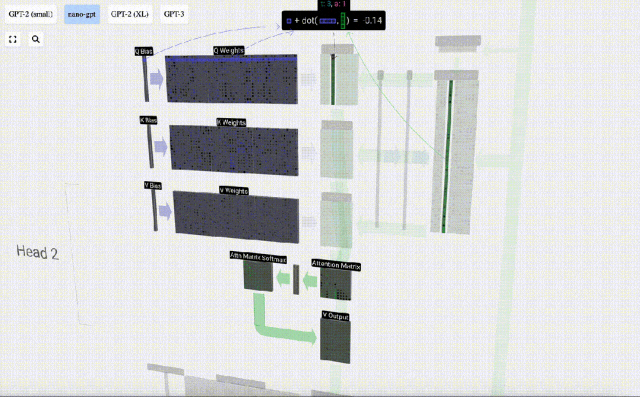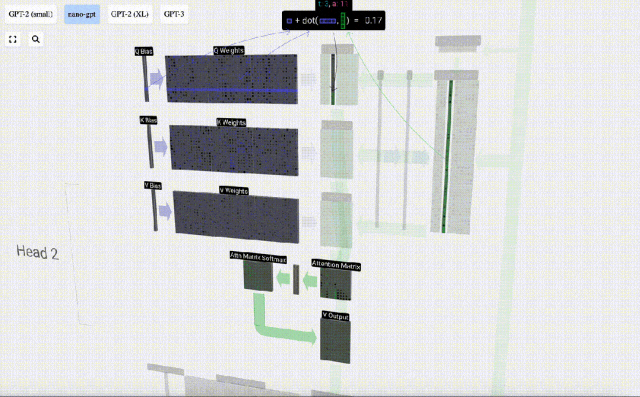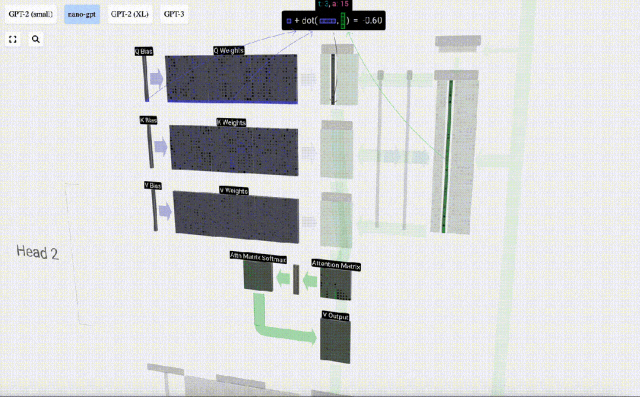
Dies ist eine allgemeine und einfache Möglichkeit, sicherzustellen, dass jedes Ausgabeelement von allen Elementen im Eingabevektor beeinflusst wird (dieser Einfluss wird durch das Gewicht bestimmt). Daher kommt es häufig in neuronalen Netzen vor.
In neuronalen Netzen tritt dieser Mechanismus häufig auf, da er es dem Modell ermöglicht, bei der Verarbeitung der Daten jeden Teil der Eingabesequenz zu berücksichtigen. Dieser umfassende Aufmerksamkeitsmechanismus ist das Herzstück vieler moderner neuronaler Netzwerkarchitekturen, insbesondere bei der Verarbeitung sequentieller Daten wie Text oder Zeitreihen.
Wir wiederholen dies für jede Ausgabeeinheit in den Vektoren Q, K, V:
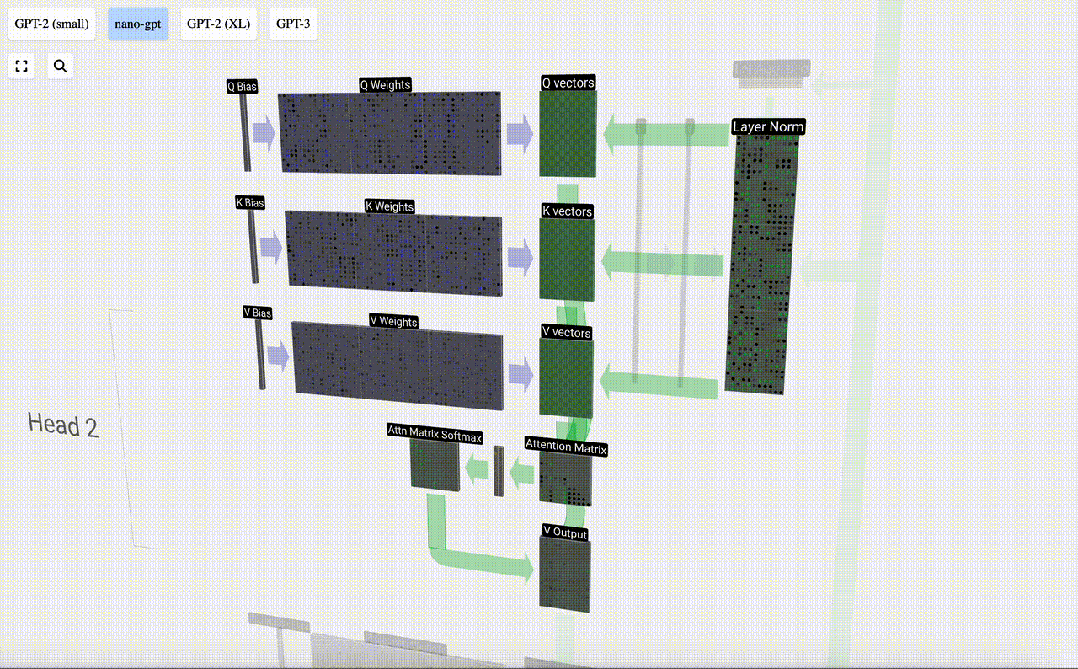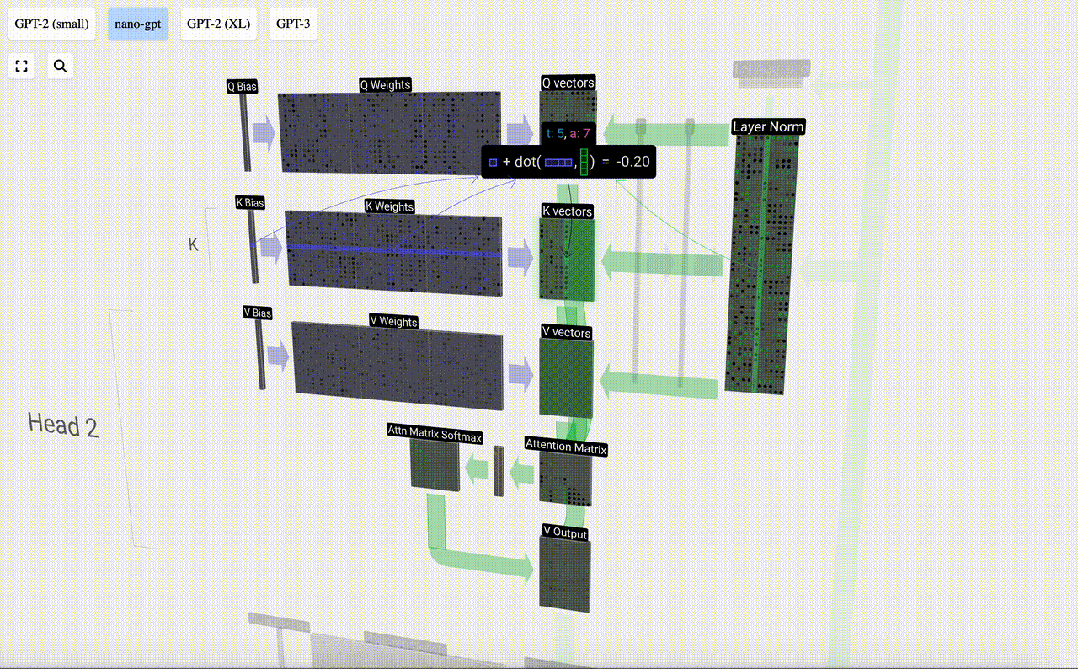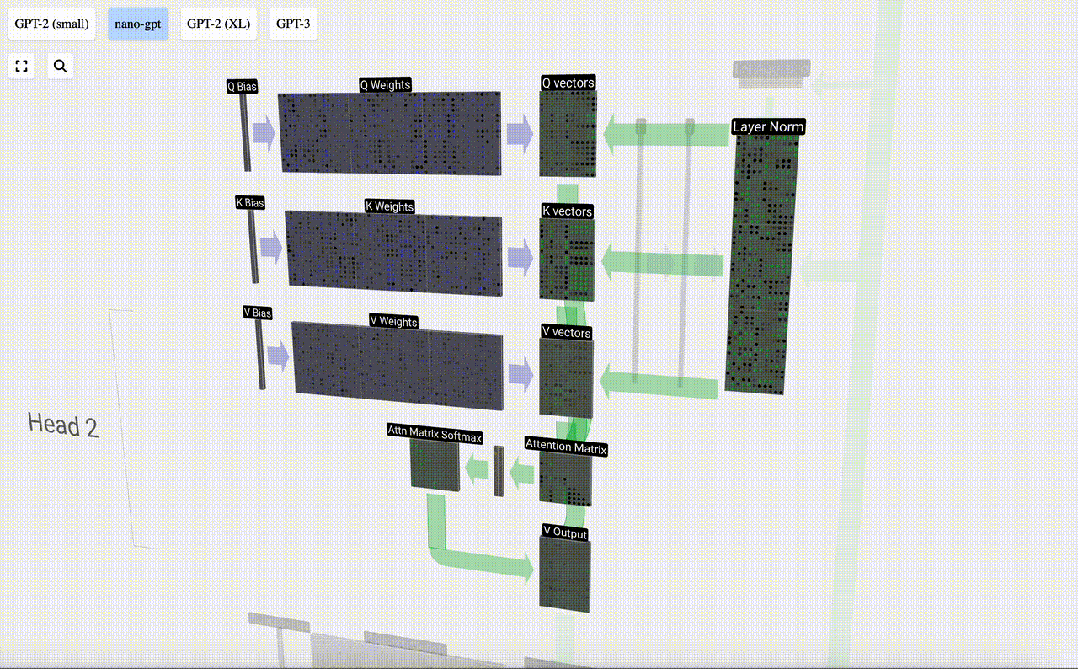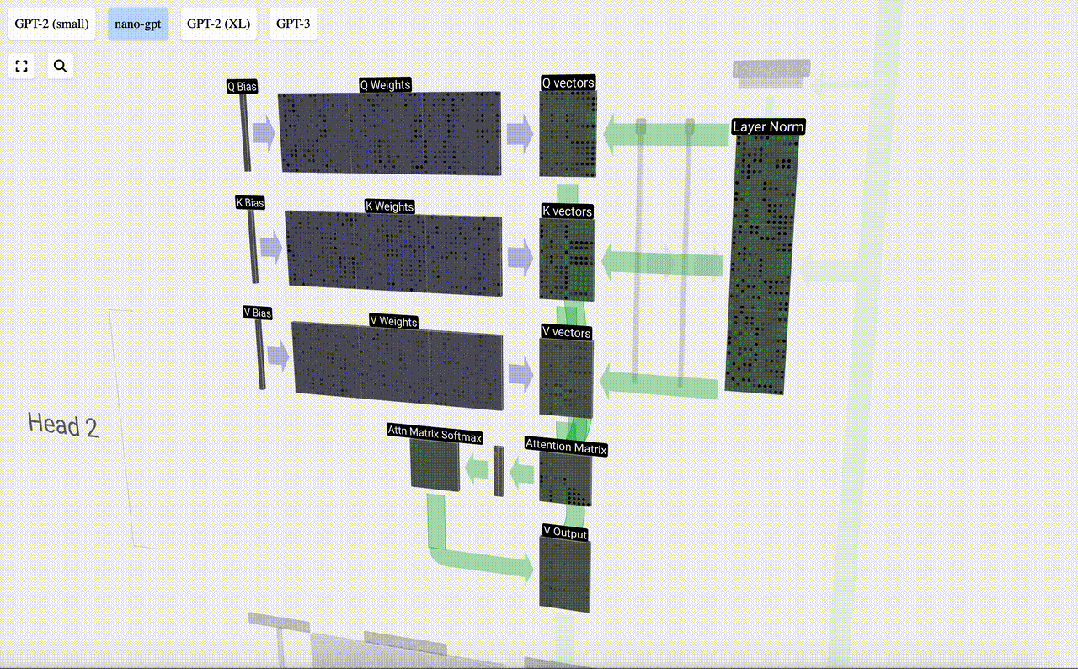
Wie verwenden wir unsere Vektoren Q (Abfrage), K (Schlüssel) und V (Wert)? Ihre Benennung gibt uns einen Hinweis: „Schlüssel“ und „Wert“ erinnern an Wörterbuchtypen, wobei Schlüssel Werten zugeordnet sind. Dann verwenden wir „Abfrage“, um den Wert zu ermitteln.

Im Fall von Selbstaufmerksamkeit geben wir statt eines einzelnen Vektors (Begriffs) eine gewichtete Kombination von Vektoren (Begriffen) zurück. Um dieses Gewicht zu finden, berechnen wir das Skalarprodukt zwischen einem Q-Vektor und jedem K-Vektor, gewichten und normalisieren es und multiplizieren es schließlich mit dem entsprechenden V-Vektor und addieren sie.

Am Beispiel der 6. Spalte (t=5) beginnt die Abfrage in dieser Spalte:
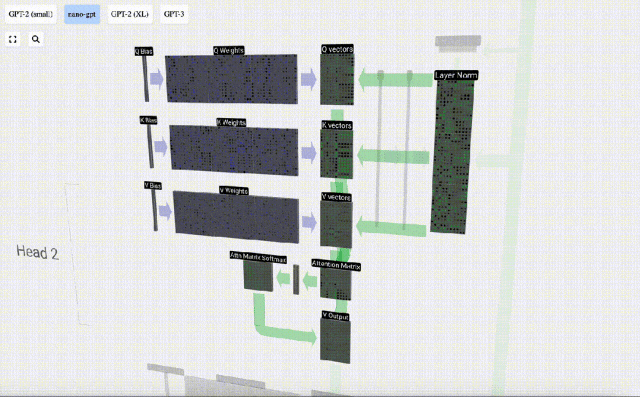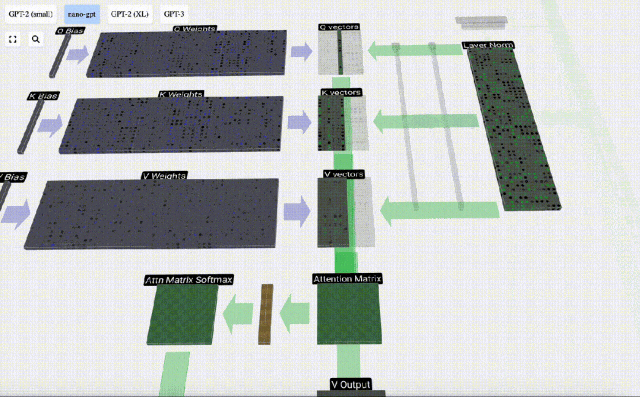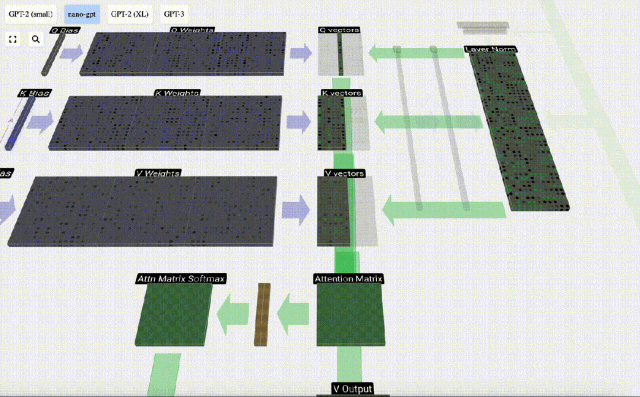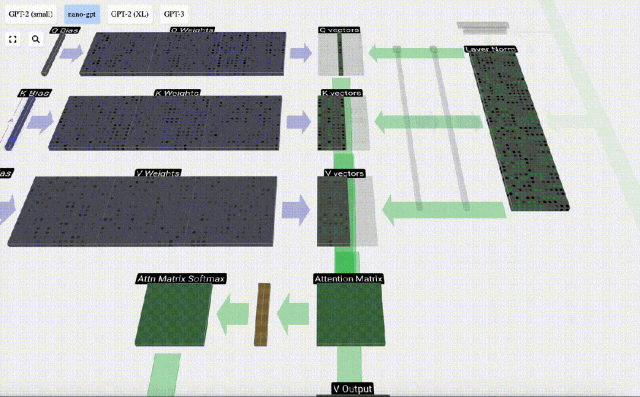
Aufgrund der Existenz einer Aufmerksamkeitsmatrix können die ersten 6 Spalten von KV abgefragt werden, und Der Q-Wert ist die aktuelle Zeit.
Berechnen Sie zunächst das Skalarprodukt zwischen dem Q-Vektor der aktuellen Spalte (t=5) und dem K-Vektor der vorherigen Spalten (die ersten 6 Spalten). Dies wird dann in der entsprechenden Zeile (t=5) der Aufmerksamkeitsmatrix gespeichert.
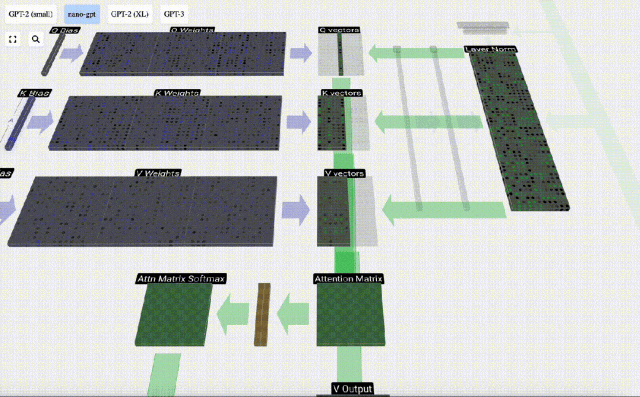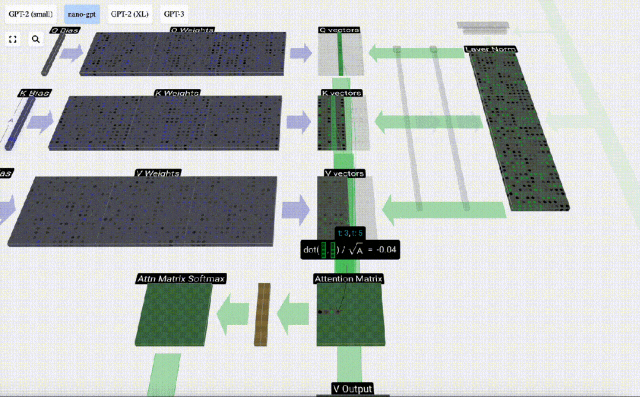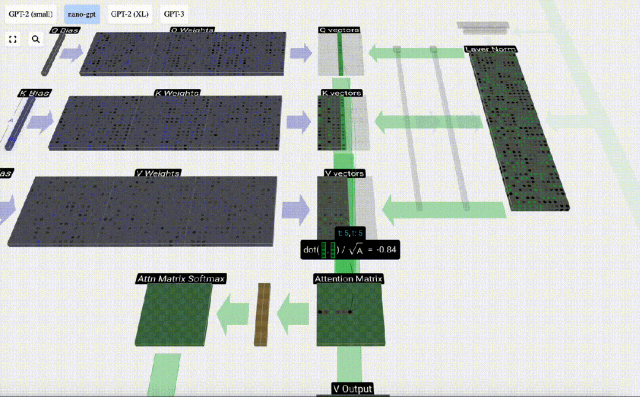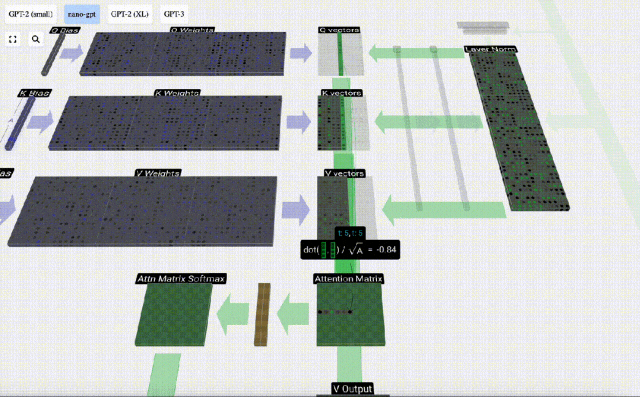
Die Größe des Skalarprodukts misst die Ähnlichkeit zwischen zwei Vektoren. Je größer das Skalarprodukt, desto ähnlicher sind sie.
Und nur der Q-Vektor wird mit dem vergangenen K-Vektor operiert, was ihn zu einer kausalen Selbstaufmerksamkeit macht. Mit anderen Worten: Token können keine „zukünftigen Informationen sehen“.
Nachdem Sie das Skalarprodukt gefunden haben, teilen Sie es durch sqrt(A), wobei A die Länge des QKV-Vektors ist. Diese Skalierung wird durchgeführt, um zu verhindern, dass große Werte den nächsten Schritt der Normalisierung (Softmax) dominieren.
Als nächstes wird die Softmax-Operation ausgeführt, um den Wertebereich auf 0 bis 1 zu reduzieren.
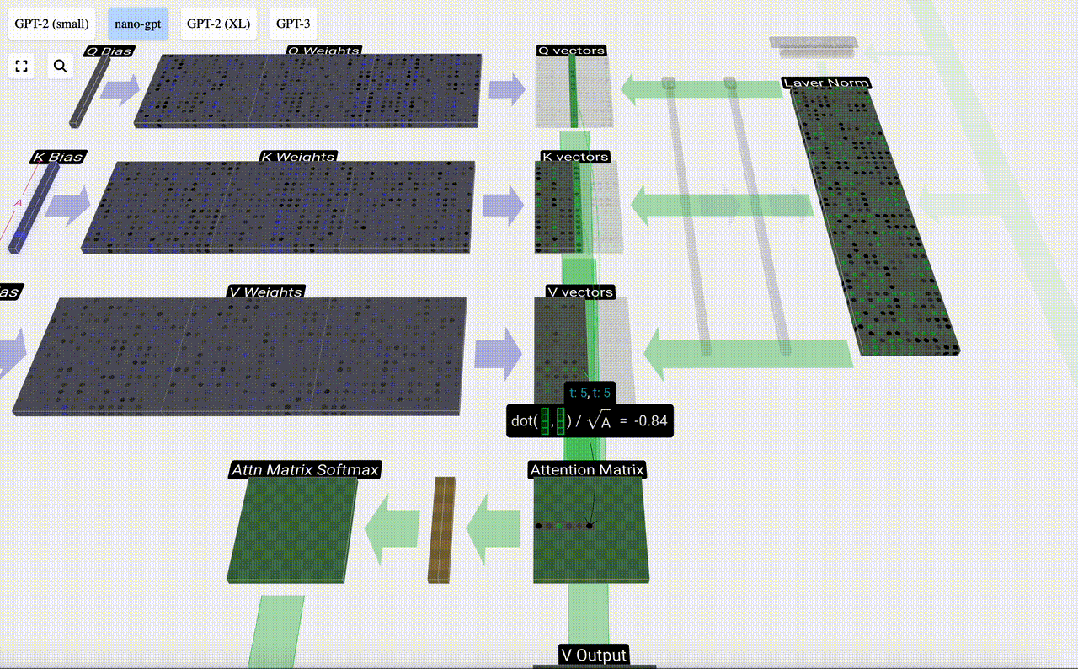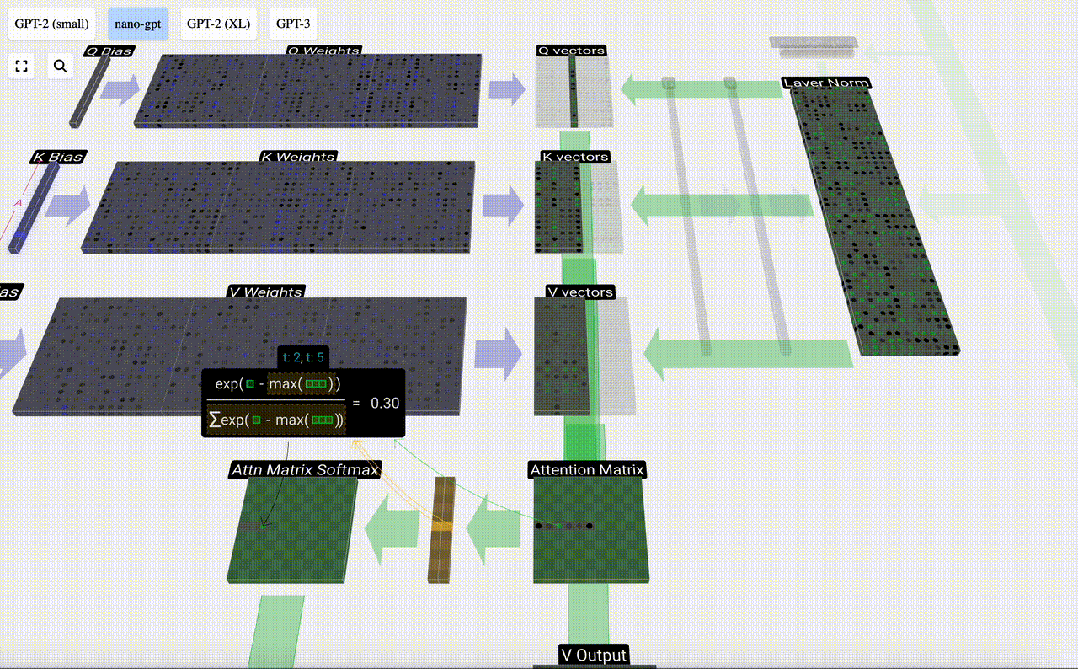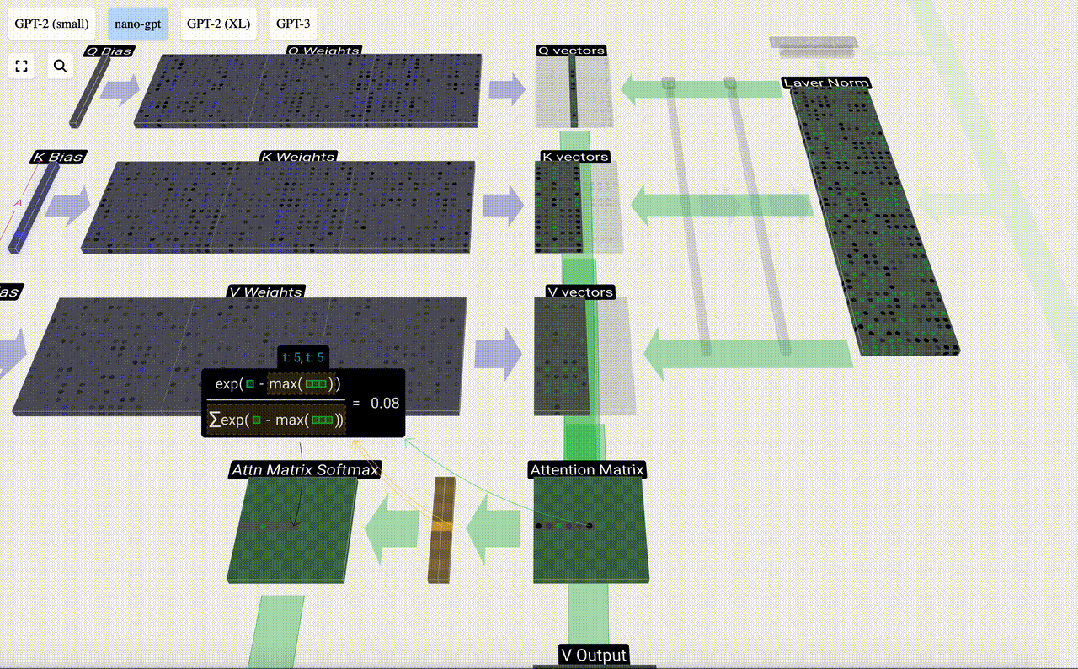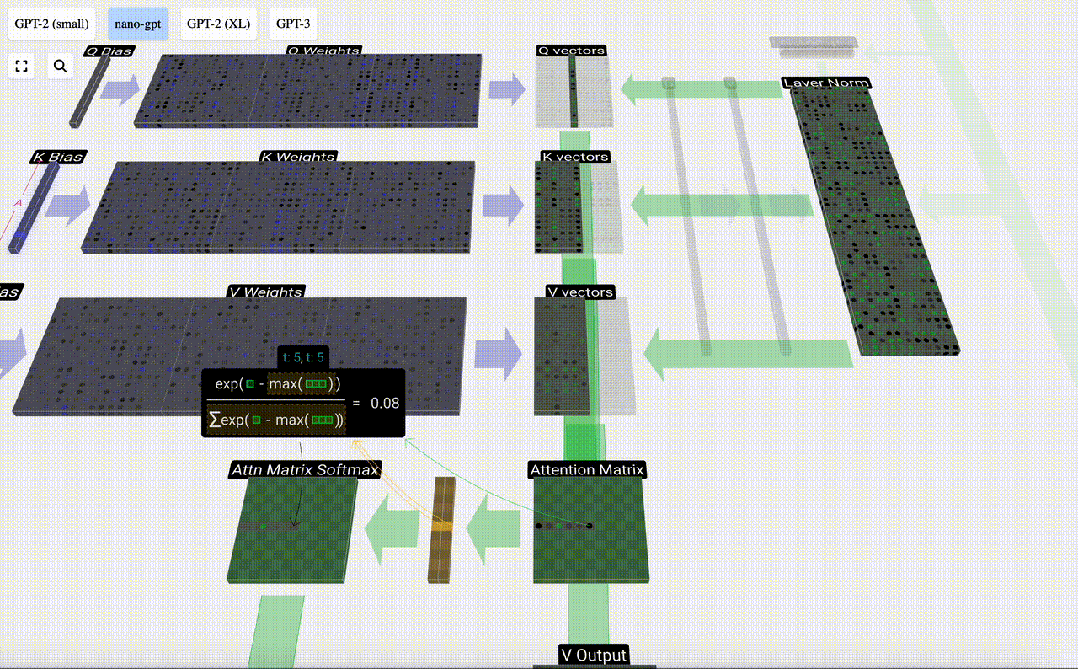
Schließlich kann der Ausgabevektor dieser Spalte (t=5) erhalten werden. Schauen Sie sich die Zeile (t=5) der normalisierten Aufmerksamkeitsmatrix an und multiplizieren Sie jedes Element mit dem entsprechenden V-Vektor der anderen Spalte.
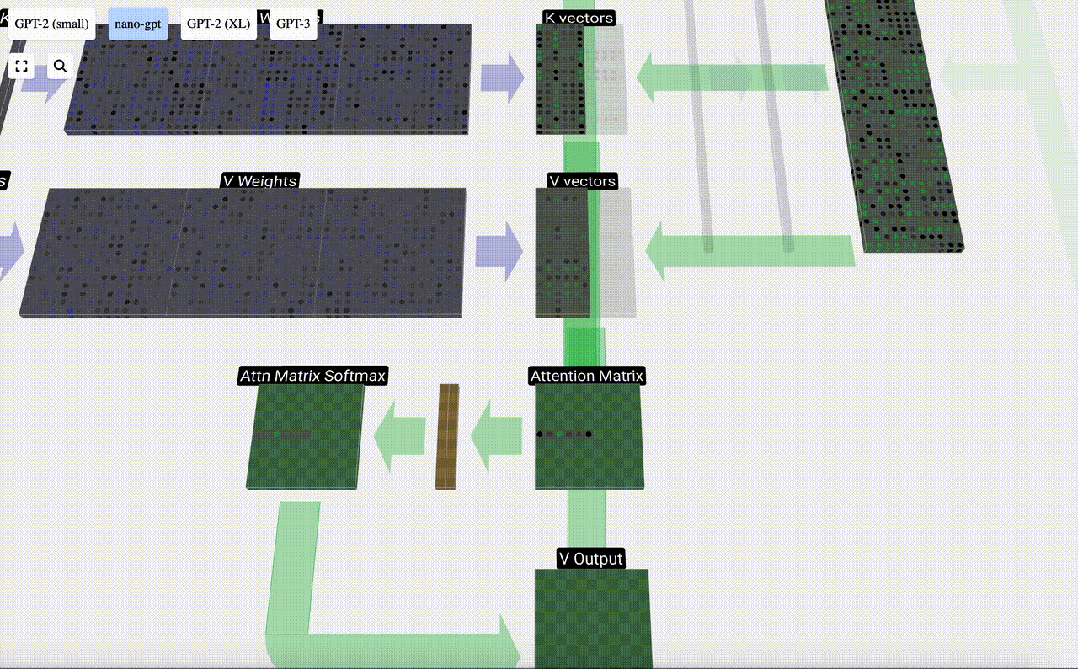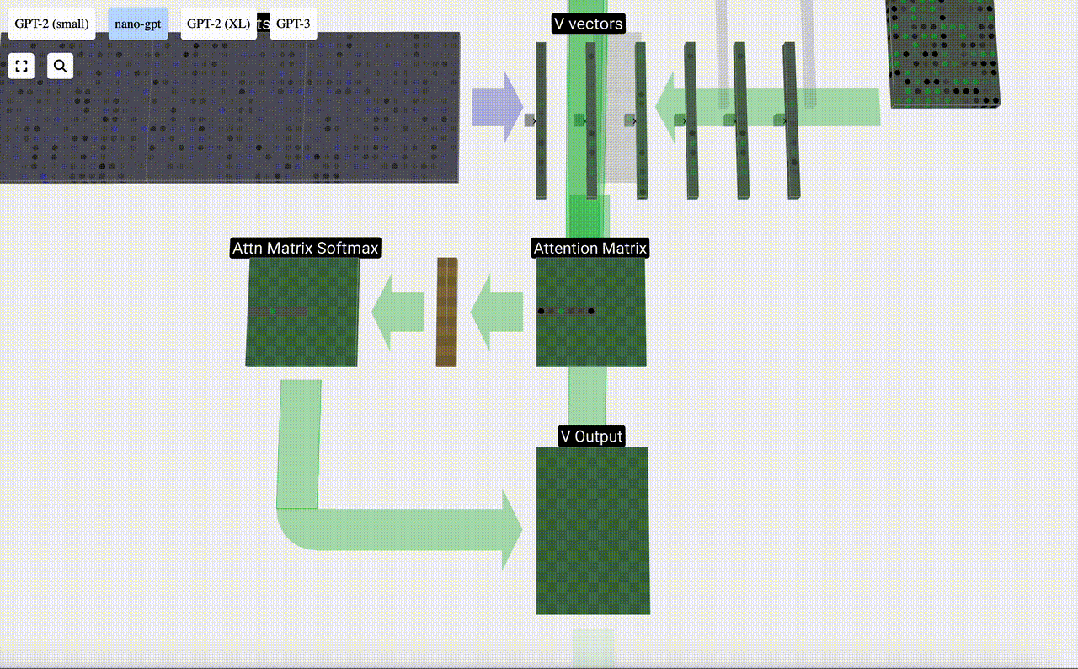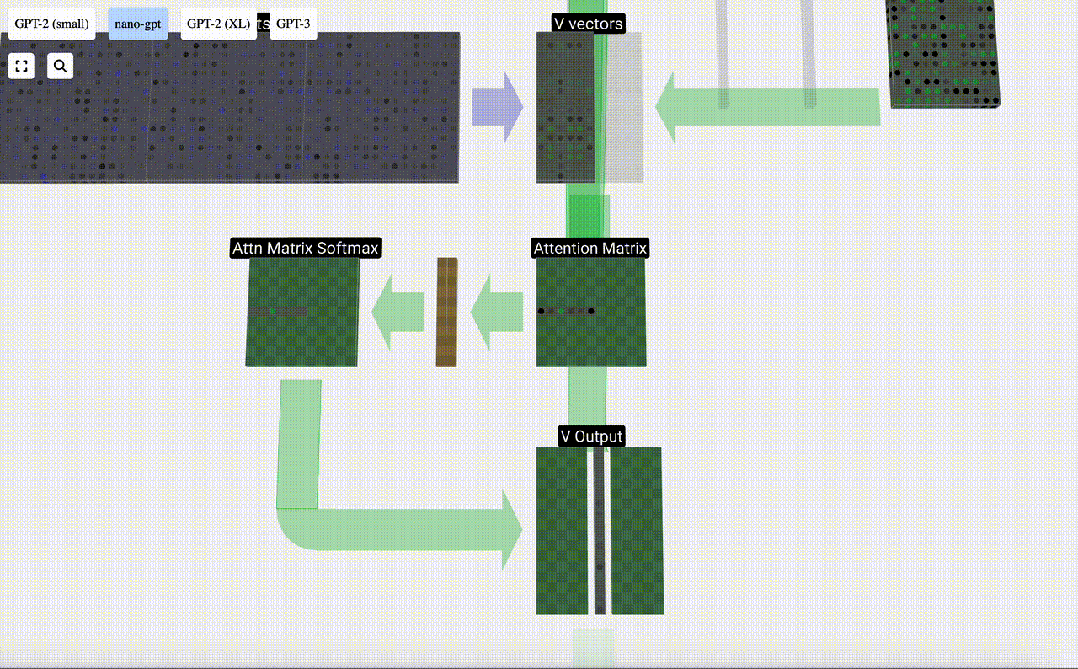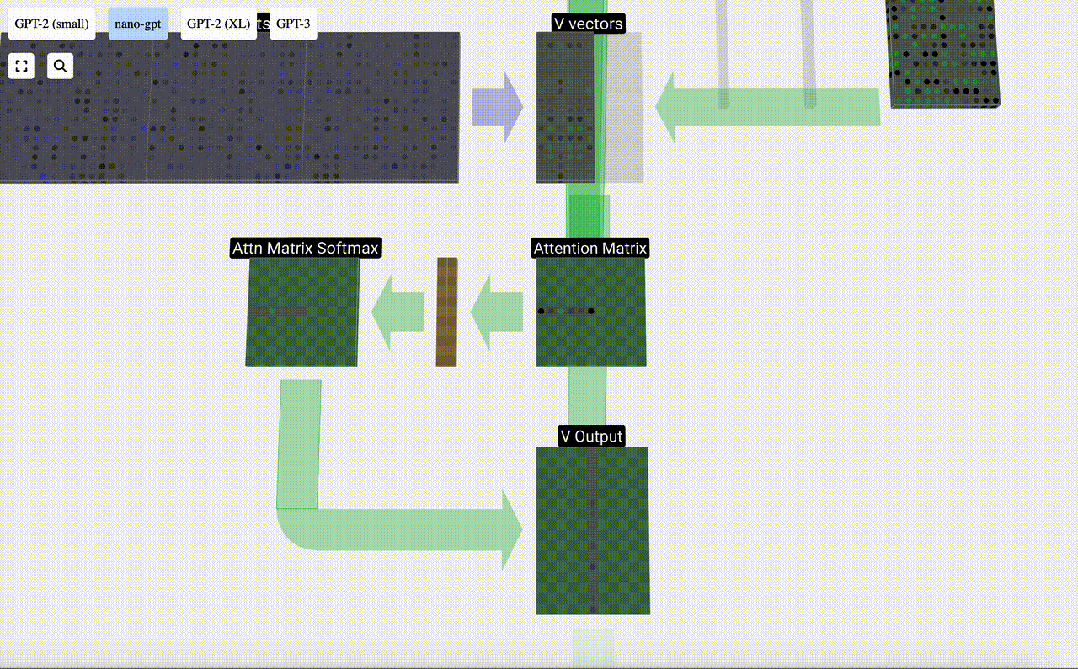
Wir können diese Vektoren dann addieren, um den Ausgabevektor zu erhalten. Daher wird der Ausgabevektor vom V-Vektor mit hoher Auflösung dominiert.
Jetzt wenden wir es auf alle Spalten an.
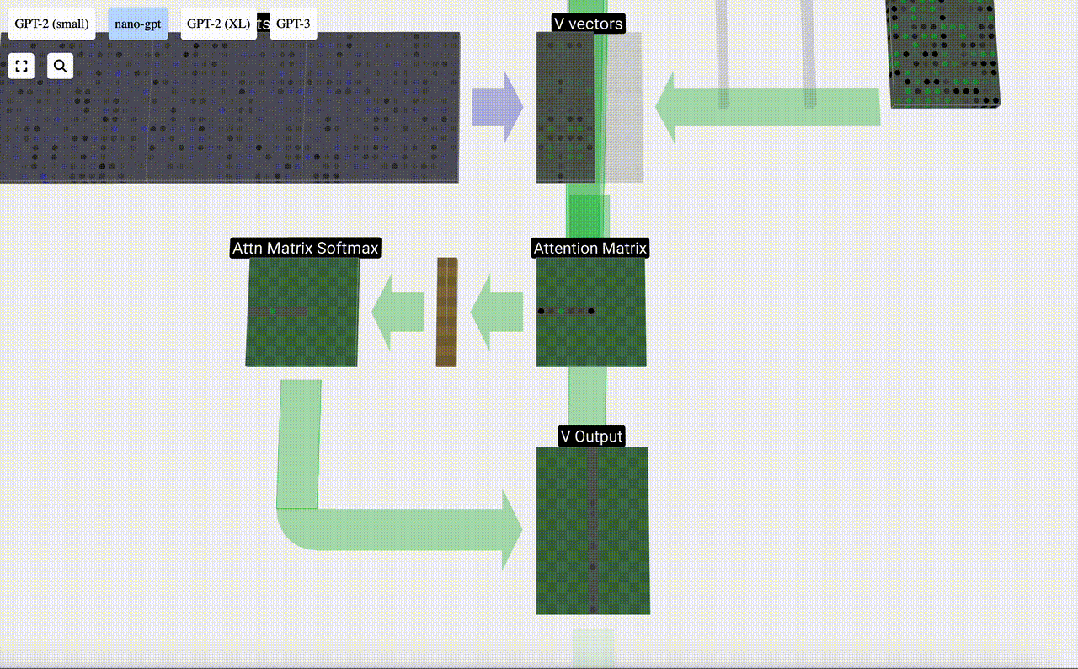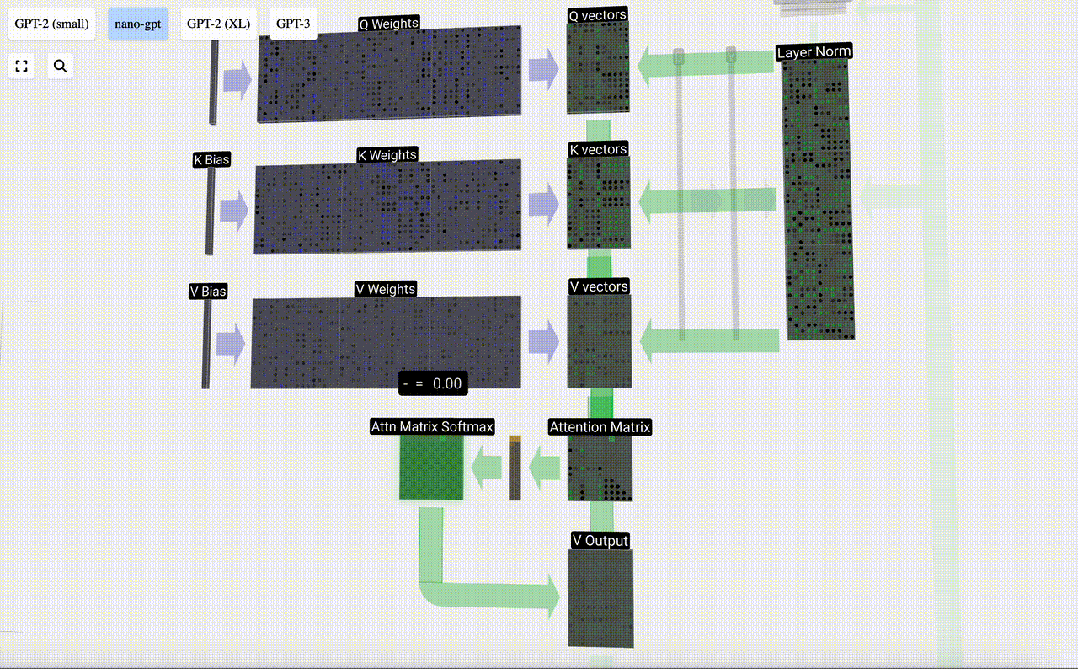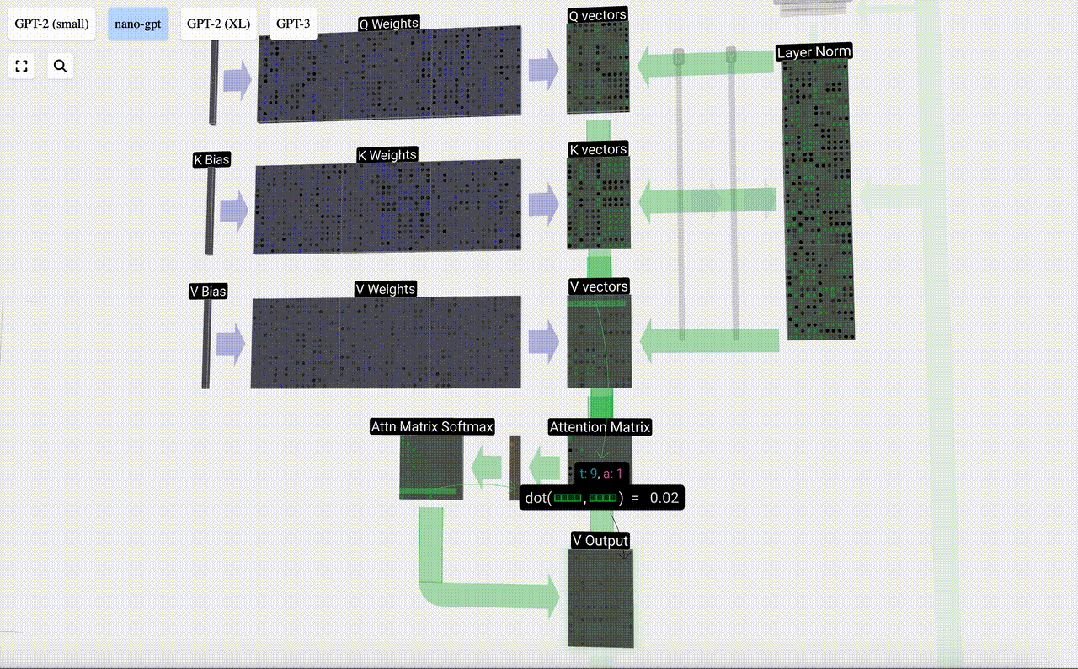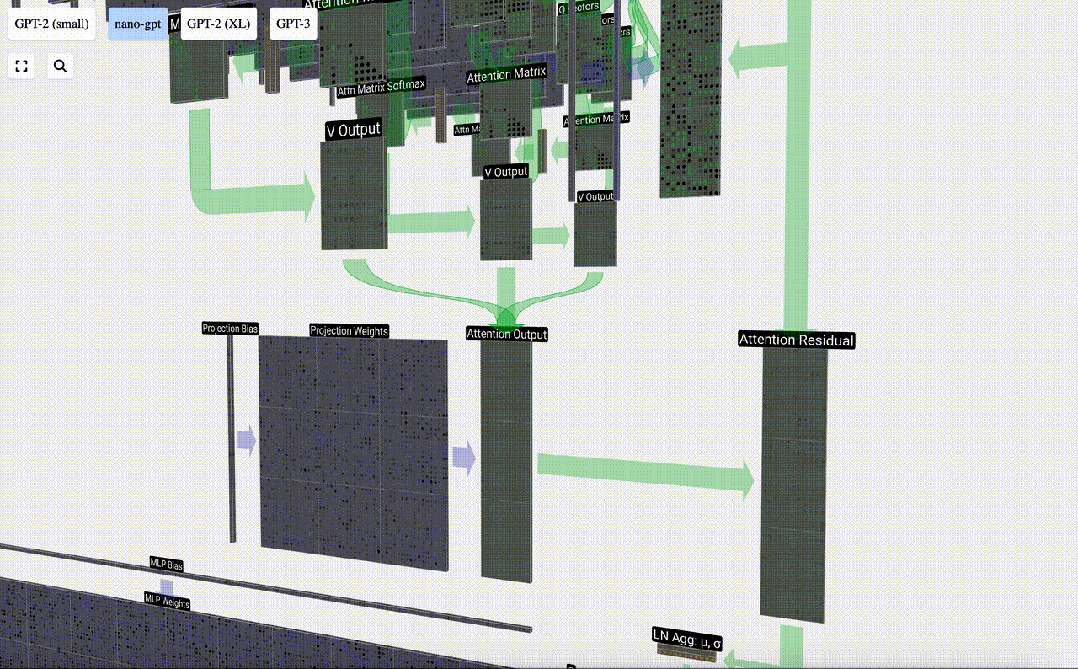
Dies ist der Verarbeitungsprozess eines Headers in der Selbstaufmerksamkeitsebene. „Das Hauptziel von Self Attention besteht also darin, dass jede Spalte relevante Informationen aus anderen Spalten finden und ihren Wert extrahieren möchte. Dies geschieht durch den Vergleich ihres Abfragevektors mit den Schlüsseln dieser anderen Spalten. Die zusätzliche Einschränkung besteht darin, dass dies nur möglich ist Schauen Sie in die Vergangenheit. „
Projektion
Nach der Selbstaufmerksamkeitsoperation erhalten wir von jedem Kopf eine Ausgabe. Bei diesen Ausgängen handelt es sich um V-Vektoren, die entsprechend gemischt und von den Q- und K-Vektoren beeinflusst werden. Um die Ausgabevektoren jedes Kopfes zusammenzuführen, stapeln wir sie einfach. Daher werden wir bei t=4 3 Vektoren mit der Länge A=16 überlagern, um 1 Vektor mit der Länge C=48 zu bilden.
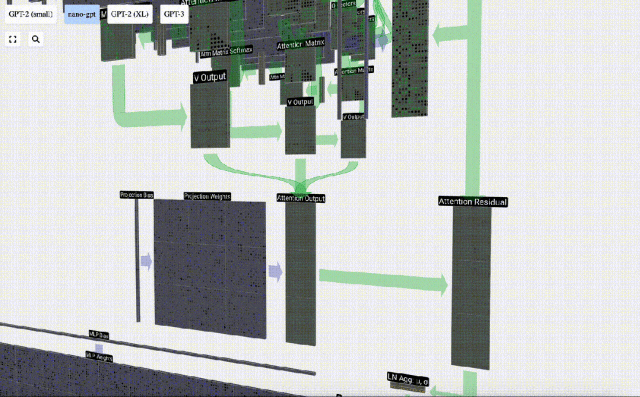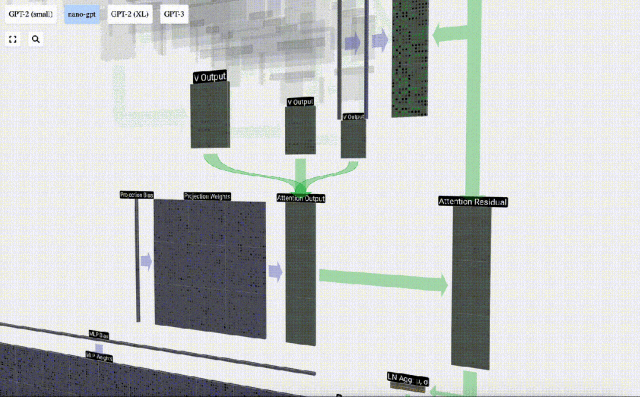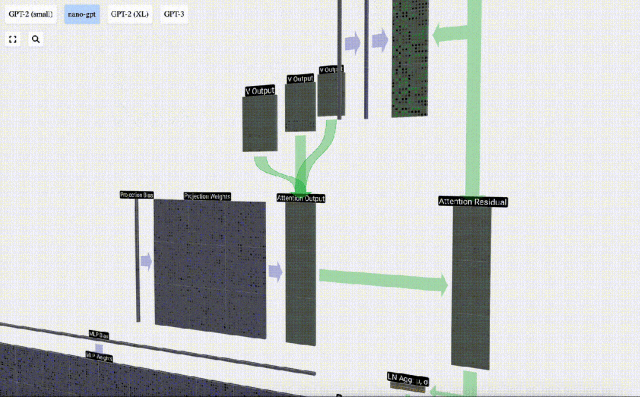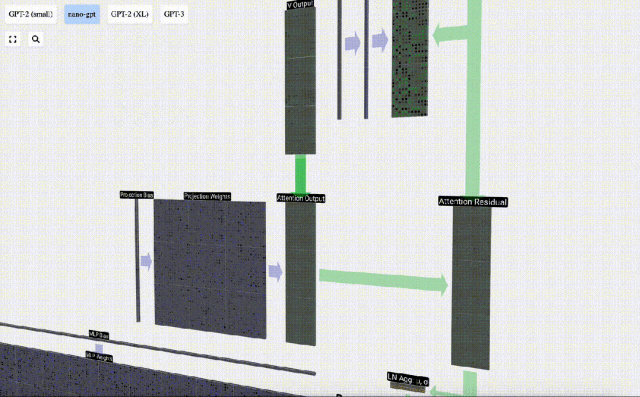
Es ist erwähnenswert, dass in GPT die Länge des Vektors innerhalb des Kopfes (A=16) gleich C/num_heads ist. Dadurch wird sichergestellt, dass wir beim erneuten Stapeln die ursprüngliche Länge C erhalten.
Auf dieser Grundlage führen wir eine Projektion durch und erhalten die Ausgabe dieser Ebene. Dies ist eine einfache Matrix-Vektor-Multiplikation pro Spalte plus einem Bias.
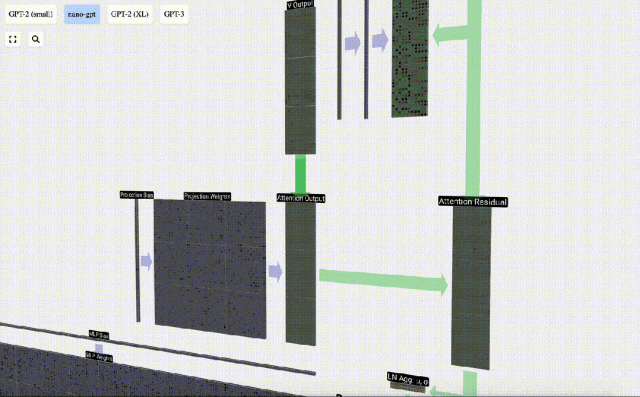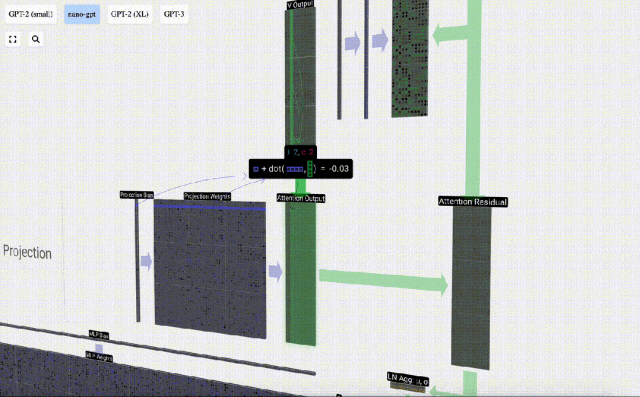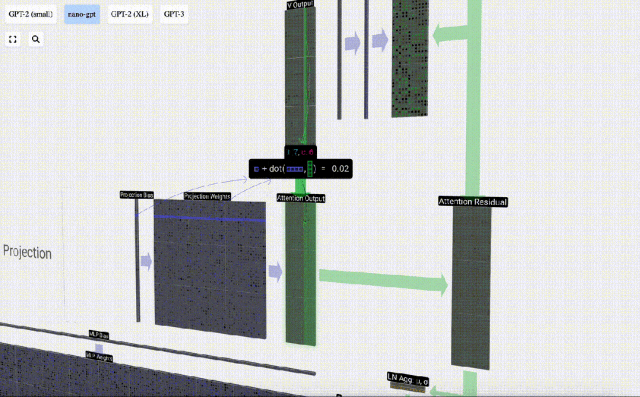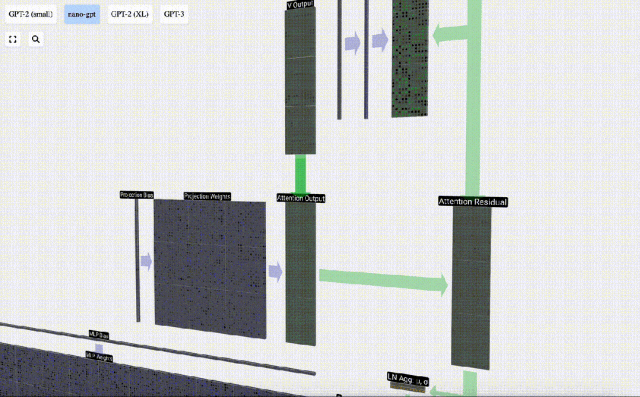
Jetzt haben wir den Output von Self Attention.
Anstatt diese Ausgabe direkt an die nächste Stufe weiterzuleiten, fügen wir sie als Element zur Eingabeeinbettung hinzu. Dieser durch den grünen vertikalen Pfeil dargestellte Vorgang wird Restverbindung oder Restpfad genannt.
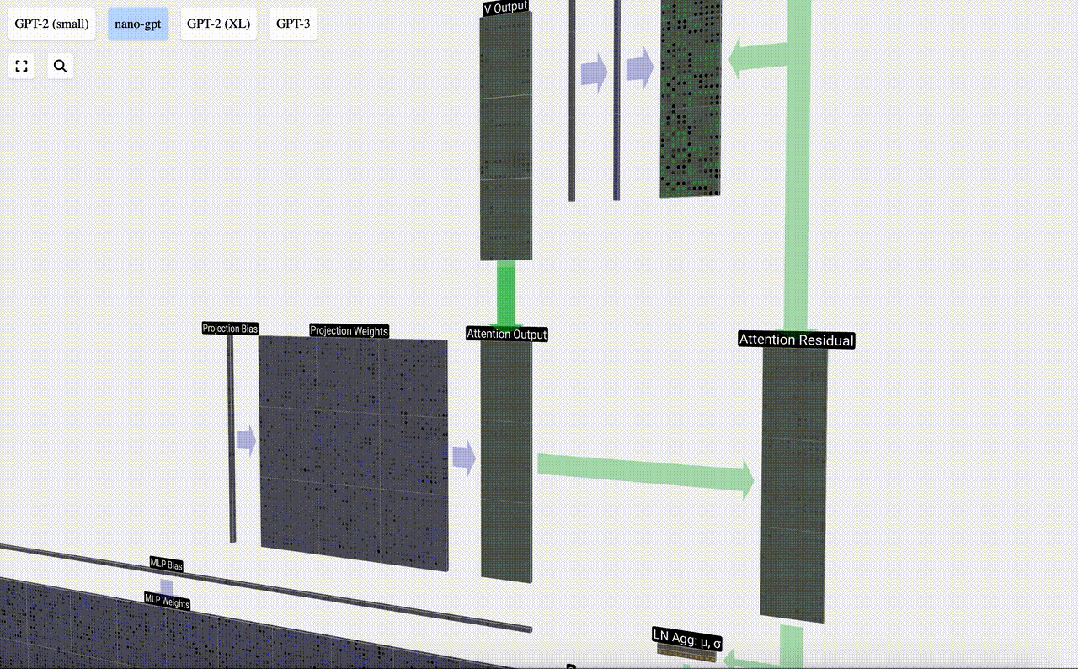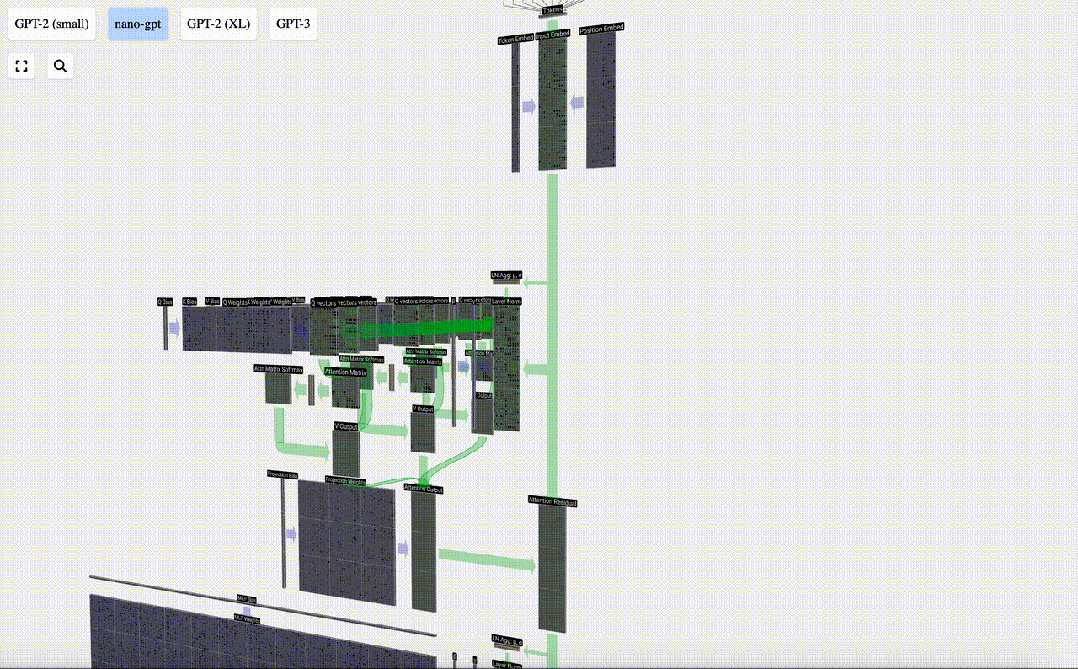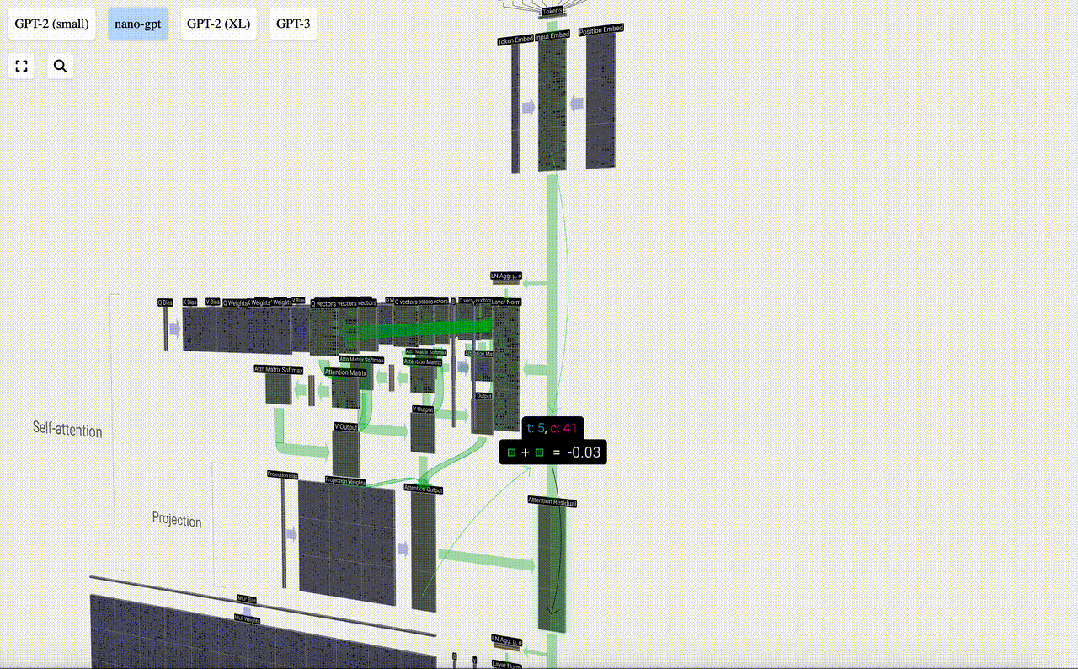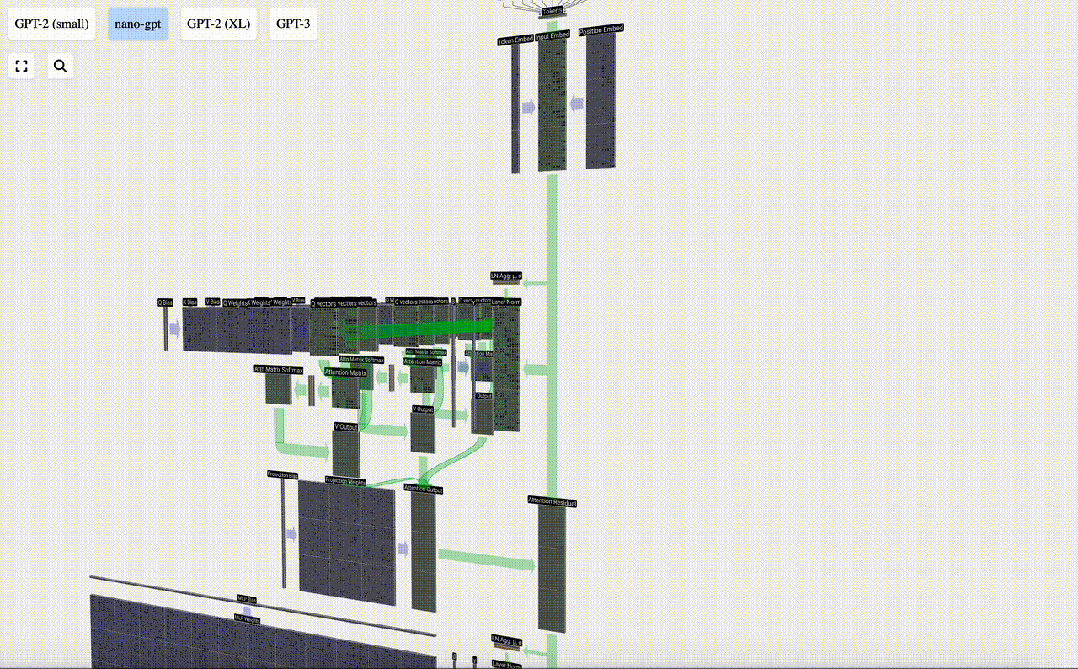
Wie die Schichtnormalisierung sind auch Restnetze von entscheidender Bedeutung, um ein effektives Lernen tiefer neuronaler Netze zu erreichen.
Da wir nun das Ergebnis der Selbstaufmerksamkeit haben, können wir es an die nächste Ebene von Transformer weitergeben: das Feedforward-Netzwerk.
Multilayer Perceptron MLP
Nach Self Attention ist der nächste Teil des Transformer-Moduls MLP (Multilayer Perceptron), hier handelt es sich um ein einfaches neuronales Netzwerk mit zwei Schichten.
Genau wie bei der Selbstaufmerksamkeit müssen wir eine Ebenennormalisierung durchführen, bevor der Vektor in das MLP eintritt.
Gleichzeitig muss in MLP die folgende Verarbeitung (unabhängig) für jeden Spaltenvektor der Länge C=48 durchgeführt werden:
- Lineare Transformation mit Bias hinzufügen (d. h. Matrix-Vektor-Multiplikation plus Bias-Operation) , umgewandelt in einen Vektor der Länge 4 * C.
- GELU-Aktivierungsfunktion (elementweise angewendet).
- Führen Sie eine lineare Transformation mit Vorspannung durch und transformieren Sie sie dann zurück in einen Vektor der Länge C.
Verfolgen wir einen der Vektoren:

Der MLP-Prozess ist wie folgt:
Führen Sie zunächst eine Matrix-Vektor-Multiplikation durch und fügen Sie Offsets hinzu, um den Vektor in eine Matrix der Länge 4*C zu erweitern. (Beachten Sie, dass die Ausgabematrix hier zur Visualisierung transponiert ist)
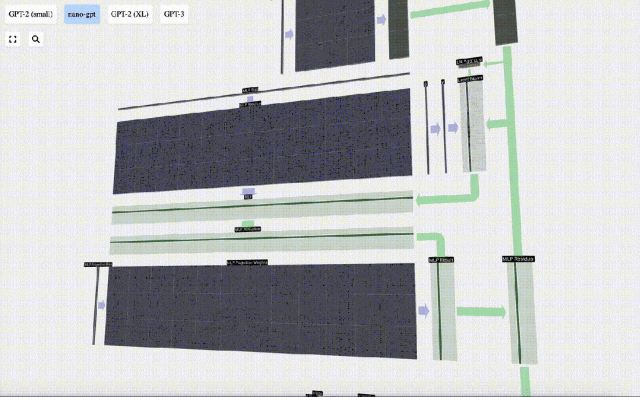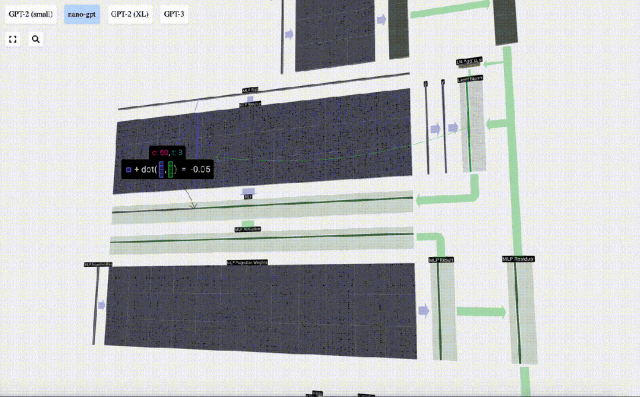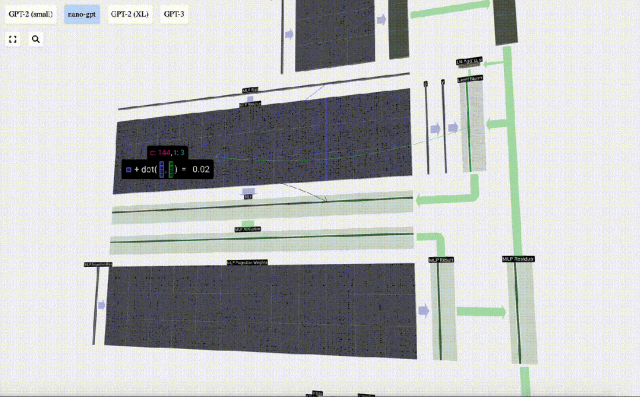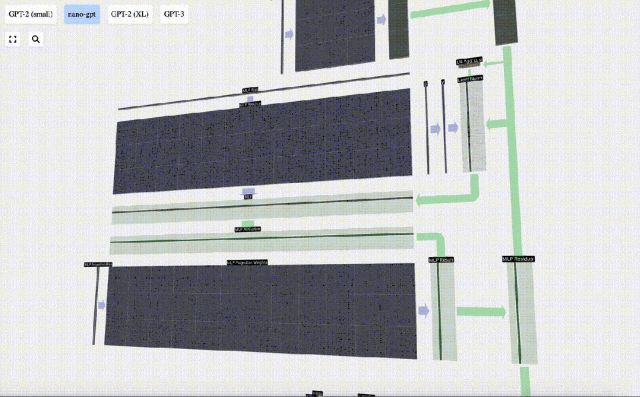
Als nächstes wenden Sie die GELU-Aktivierungsfunktion auf jedes Element des Vektors an. Dies ist ein wichtiger Bestandteil jedes neuronalen Netzwerks. Wir müssen eine gewisse Nichtlinearität in das Modell einführen. Die speziell verwendete Funktion GELU ähnelt stark der ReLU-Funktion max(0, x), weist jedoch eine glatte Kurve anstelle scharfer Ecken auf.
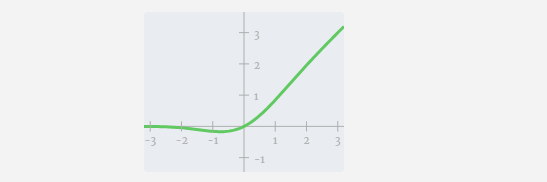
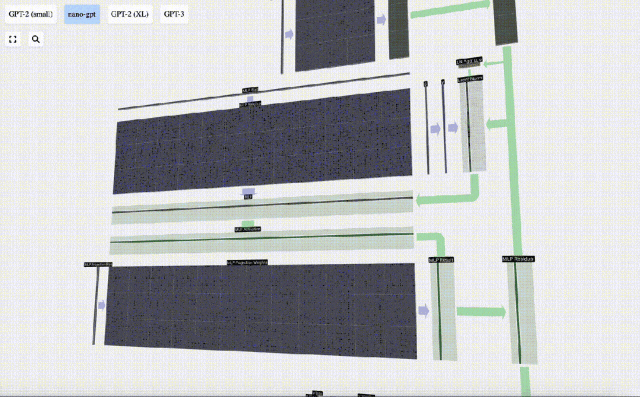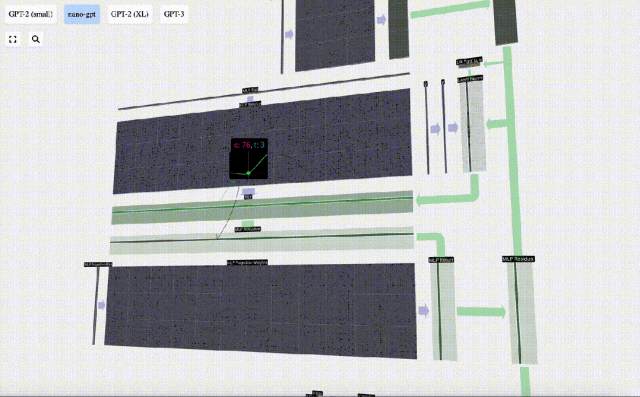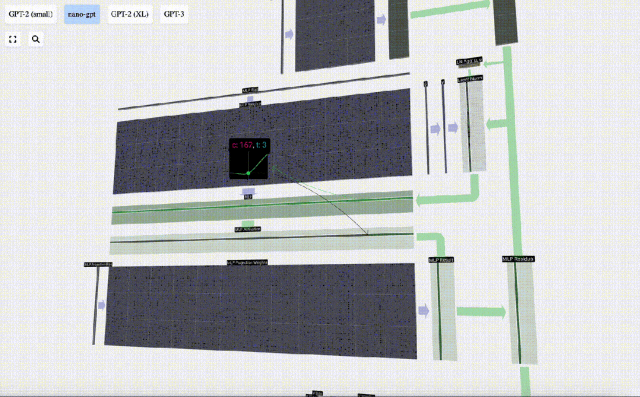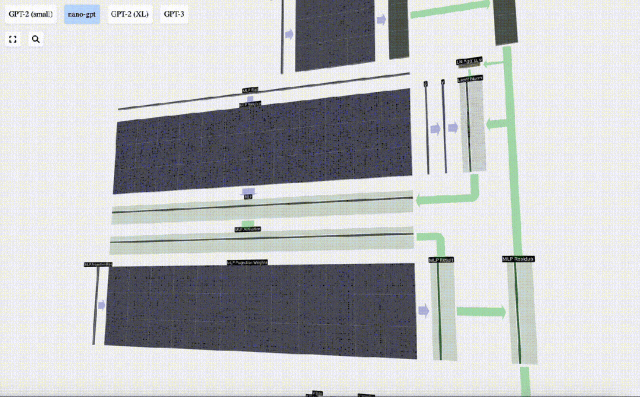
Projizieren Sie dann den Vektor über eine weitere voreingenommene Matrix-Vektor-Multiplikation zurück auf die Länge C.
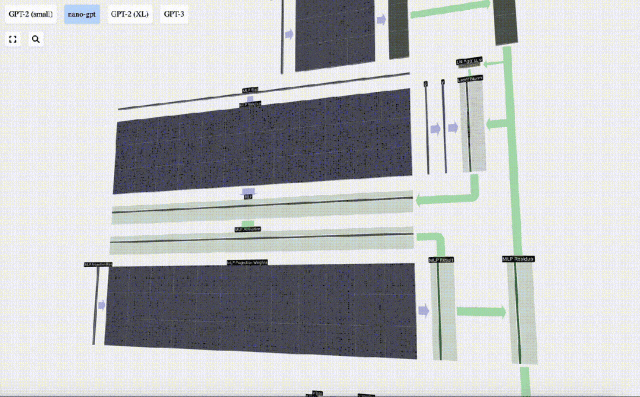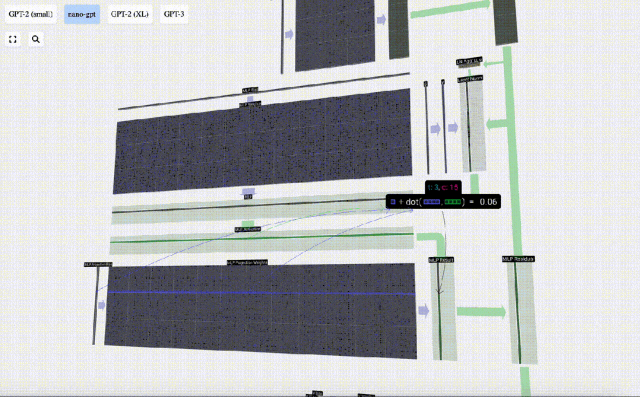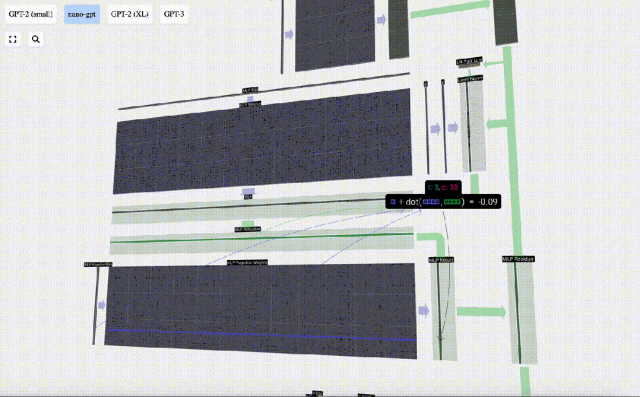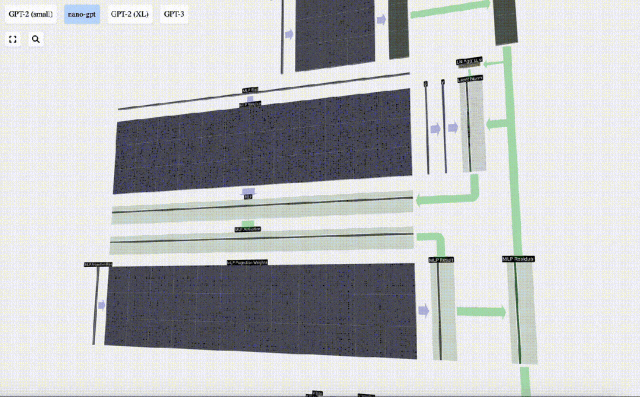
Auch hier gibt es ein Restnetzwerk. Wie beim Teil Selbstaufmerksamkeit + Projektion fügen wir die Ergebnisse des MLP in der Reihenfolge der Elemente zur Eingabe hinzu.
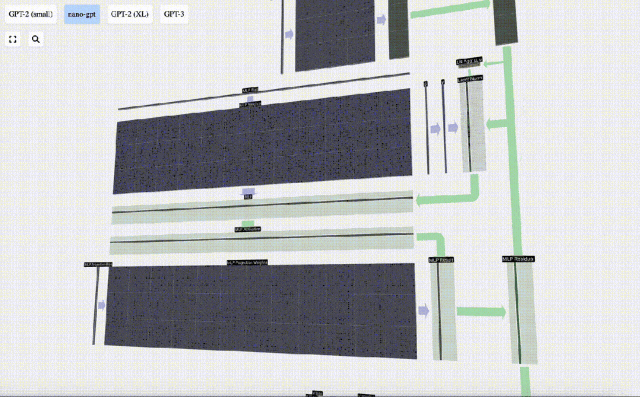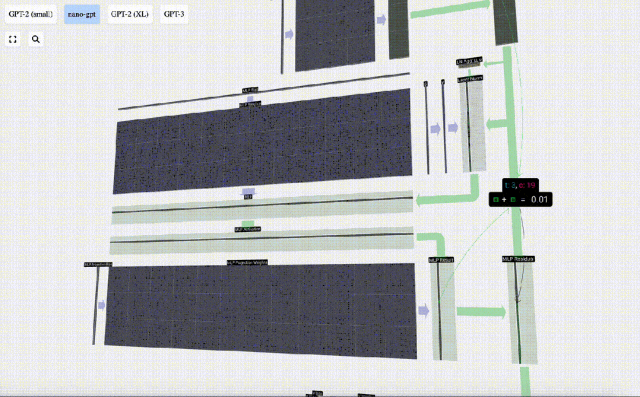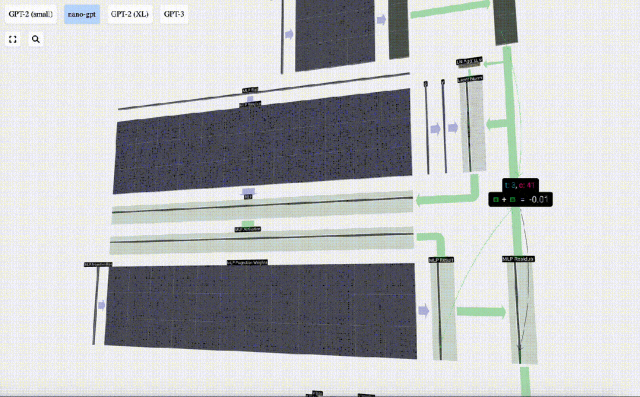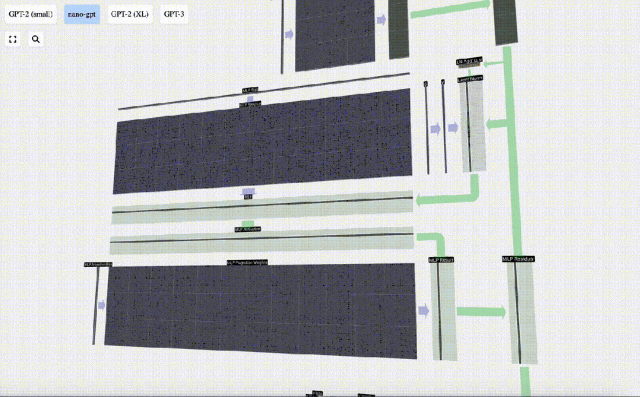
Wiederholen Sie diese Vorgänge.
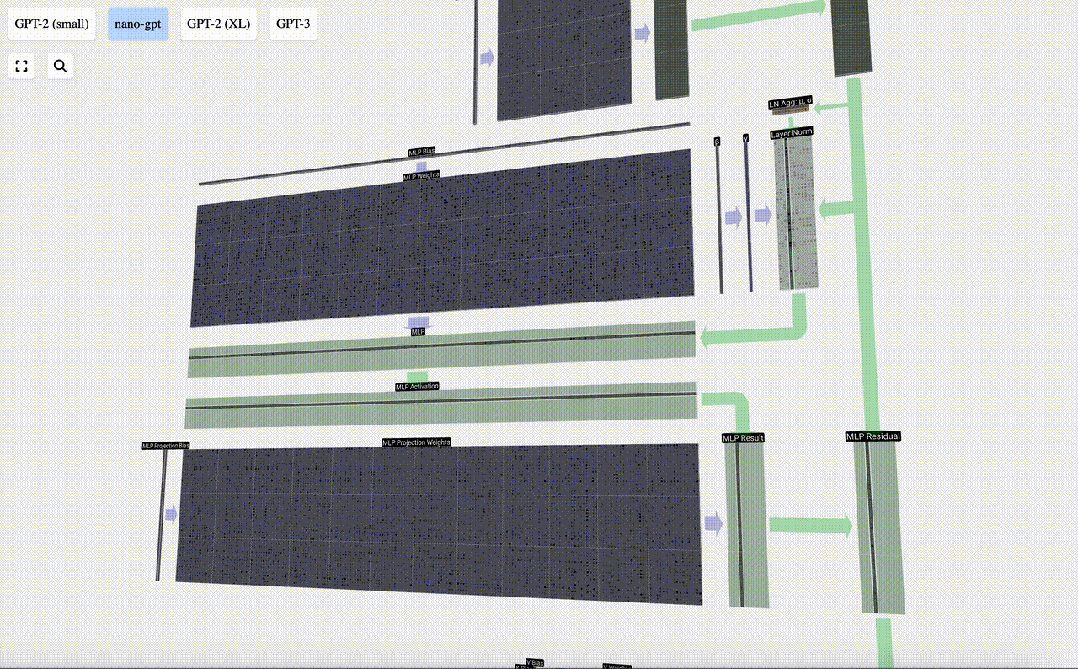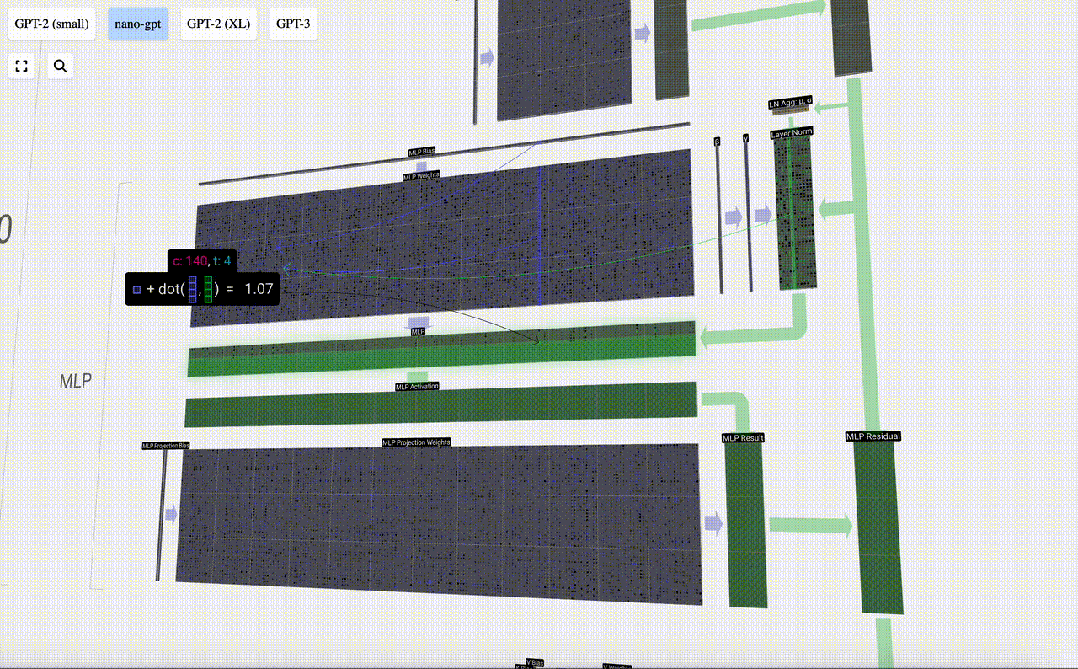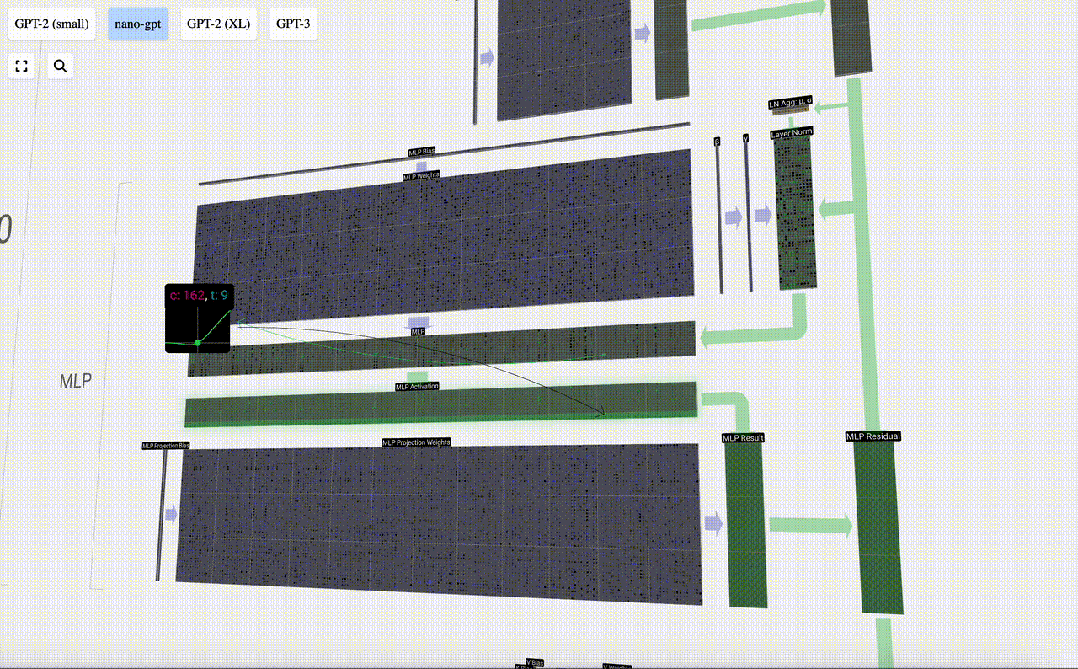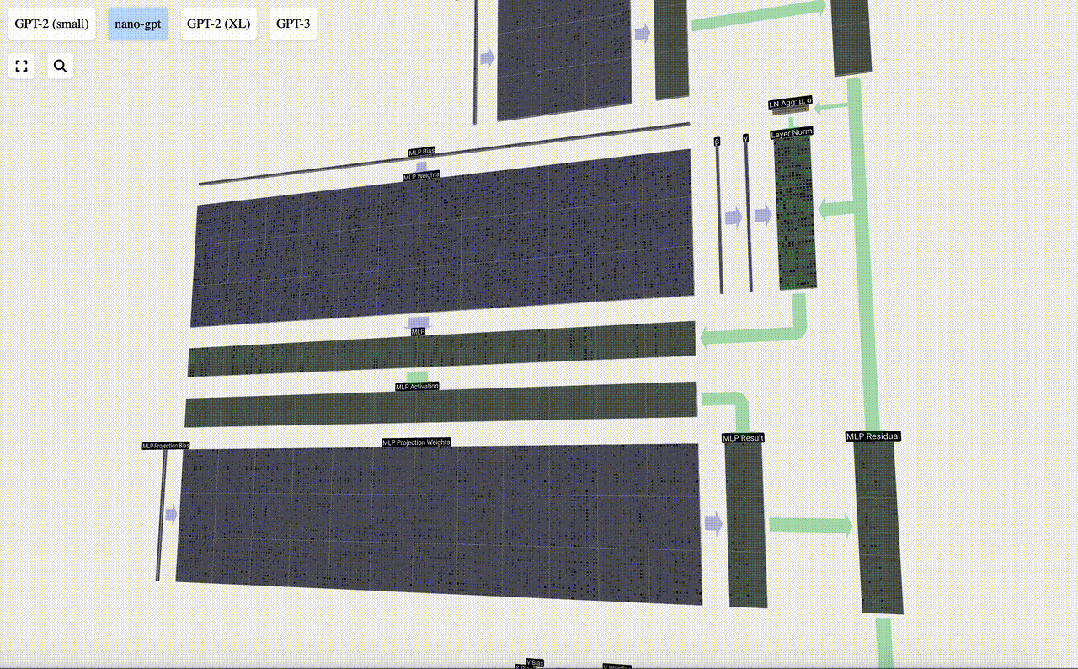
Dies ist das Ende der MLP-Schicht und wir erhalten endlich die Ausgabe des Transformators.
Transformer
Dies ist ein vollständiges Transformer-Modul!
Diese verschiedenen Module bilden den Hauptteil jedes GPT-Modells, und der Ausgang jedes Moduls ist der Eingang des nächsten Moduls.
Wie beim Deep Learning üblich, ist es schwierig, genau zu sagen, was jede dieser Schichten tut, aber wir haben einige allgemeine Ideen: Frühere Schichten neigen dazu, sich auf das Erlernen von Merkmalen und Mustern auf niedriger Ebene zu konzentrieren, während spätere Schichten auf das Erkennen und Verstehen höherer Ebenen abzielen Abstraktionen und Beziehungen auf -Ebene. Im Kontext der Verarbeitung natürlicher Sprache können niedrigere Schichten Grammatik, Syntax und einfache lexikalische Assoziationen lernen, während höhere Schichten komplexere semantische Beziehungen, Diskursstrukturen und kontextabhängige Bedeutungen erfassen können.
Softmax
Der letzte Schritt ist die Softmax-Operation, die die vorhergesagte Wahrscheinlichkeit jedes Tokens ausgibt.
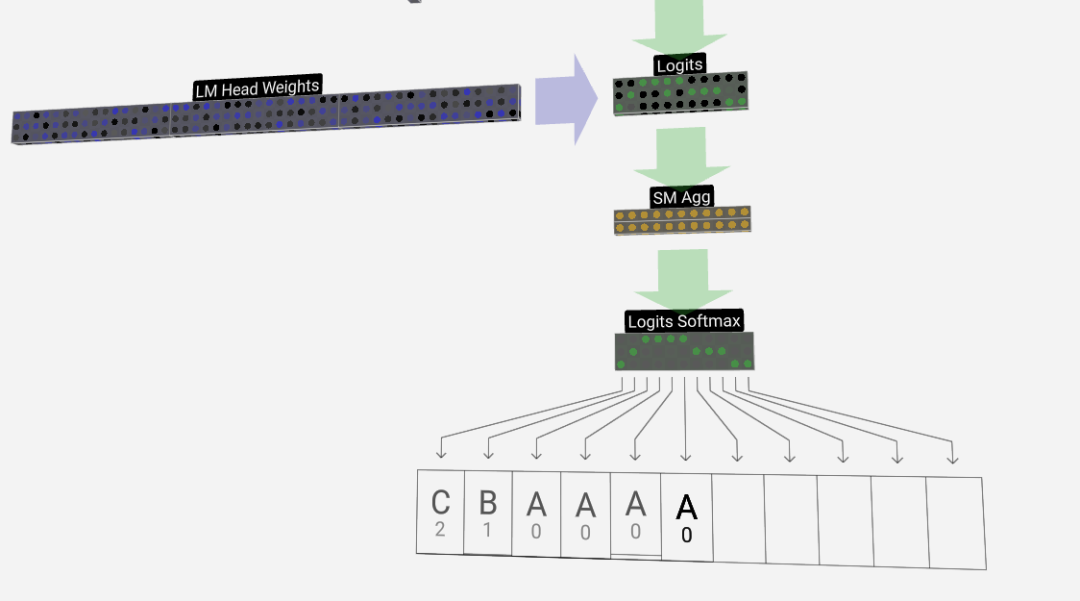
Ausgabe
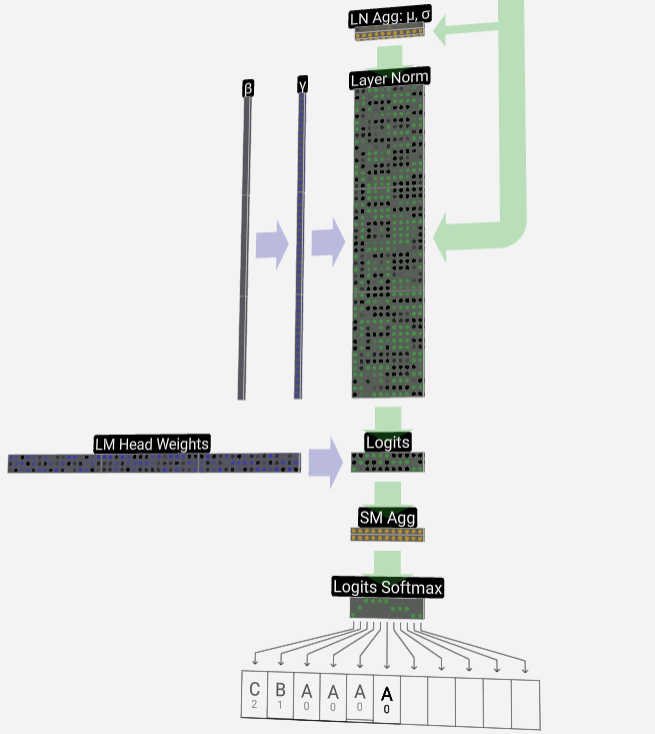
Endlich erreichen wir das Ende des Modells. Die Ausgabe des letzten Transformers durchläuft eine Regularisierungsschicht, gefolgt von einer unverzerrten linearen Transformation.
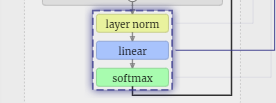
Diese letzte Transformation wandelt jeden unserer Spaltenvektoren von der Länge C in die wortschatzgroße Länge nvocab um. Es werden also tatsächlich für jedes Wort im Vokabular Score-Logits generiert.
Um diese Ergebnisse in intuitivere Wahrscheinlichkeitswerte umzuwandeln, müssen sie zuerst durch Softmax verarbeitet werden. Für jede Spalte erhalten wir also die Wahrscheinlichkeit, dass das Modell jedem Wort im Vokabular zugeordnet ist.
In diesem speziellen Modell hat es tatsächlich alle Antworten zur Reihenfolge der drei Buchstaben gelernt, sodass die Wahrscheinlichkeiten stark in Richtung der richtigen Antwort tendieren.
Wenn wir das Modell im Laufe der Zeit voranschreiten lassen, müssen wir die Wahrscheinlichkeit der letzten Spalte verwenden, um über den nächsten hinzugefügten Token in der Sequenz zu entscheiden. Wenn wir beispielsweise sechs Token in das Modell eingeben, würden wir die Ausgabewahrscheinlichkeiten in Spalte sechs verwenden.
Die Ausgabe dieser Spalte ist eine Reihe von Wahrscheinlichkeitswerten, und wir müssen tatsächlich einen davon als nächsten Token in der Sequenz auswählen. Dies erreichen wir durch „Stichproben aus der Verteilung“, das heißt durch die zufällige Auswahl eines Tokens basierend auf seiner Wahrscheinlichkeit. Beispielsweise hat ein Token mit einer Wahrscheinlichkeit von 0,9 eine Wahrscheinlichkeit von 90 %, ausgewählt zu werden. Wir haben jedoch auch andere Möglichkeiten, wie zum Beispiel immer den Token mit der höchsten Wahrscheinlichkeit zu wählen.
Wir können die „Glätte“ der Verteilung auch über den Temperaturparameter steuern. Höhere Temperaturen führen zu einer gleichmäßigeren Verteilung, während niedrigere Temperaturen zu einer stärkeren Konzentration auf die Token mit der höchsten Wahrscheinlichkeit führen.
Wir passen die Logits (die Ausgabe der linearen Transformation) mithilfe des Temperaturparameters an, bevor wir Softmax anwenden, da die Potenzierung in Softmax einen deutlich verstärkenden Effekt auf größere Werte hat und eine Annäherung aller Werte diesen Effekt verringert.
 Bilder
Bilder
Das obige ist der detaillierte Inhalt vonDurchbrechen Sie die Informationsbarriere! Schockierendes großformatiges 3D-Visualisierungstool wird veröffentlicht!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1389
1389
 52
52
 Rexas Finance (RXS) kann Solana (SOL), Cardano (ADA), XRP und Dogecoin (Doge) im Jahr 2025 übertreffen
Apr 21, 2025 pm 02:30 PM
Rexas Finance (RXS) kann Solana (SOL), Cardano (ADA), XRP und Dogecoin (Doge) im Jahr 2025 übertreffen
Apr 21, 2025 pm 02:30 PM
Auf dem volatilen Kryptowährungsmarkt suchen Anleger nach Alternativen, die über die beliebten Währungen hinausgehen. Obwohl bekannte Kryptowährungen wie Solana (SOL), Cardano (ADA), XRP und Doge (DOGE) auch Herausforderungen wie Marktgefühle, regulatorische Unsicherheit und Skalierbarkeit gegenübersehen. Ein neues aufstrebendes Projekt, Rexasfinance (RXS), entsteht jedoch. Es stützt sich nicht auf Prominenteffekte oder Hype, sondern konzentriert sich auf die Kombination der realen Vermögenswerte (RWA) mit Blockchain-Technologie, um den Anlegern eine innovative Möglichkeit zum Investieren zu bieten. Diese Strategie hofft, eines der erfolgreichsten Projekte von 2025 zu sein. Rexasfi
 Global Asset startet ein neues kI-gesteuertes intelligentes Handelssystem, um die globale Handelseffizienz zu verbessern
Apr 20, 2025 pm 09:06 PM
Global Asset startet ein neues kI-gesteuertes intelligentes Handelssystem, um die globale Handelseffizienz zu verbessern
Apr 20, 2025 pm 09:06 PM
Global Assets startet ein neues KI -intelligentes Handelssystem, um die neue Ära der Handelseffizienz zu leiten! Die bekannte umfassende Handelsplattform Global Assets hat sein KI-intelligentes Handelssystem offiziell gestartet, um technologische Innovationen zu nutzen, um die globale Handelseffizienz zu verbessern, die Benutzererfahrung zu optimieren und zum Aufbau einer sicheren und zuverlässigen globalen Handelsplattform beizutragen. Der Schritt ist ein wichtiger Schritt für globale Vermögenswerte im Bereich der Smart Finance, wodurch die globale Marktführung weiter konsolidiert wird. Eröffnung einer neuen Ära von technologiebetriebenen und offenen intelligenten Handel. Vor dem Hintergrund der eingehenden Entwicklung von Digitalisierung und Intelligenz nimmt die Abhängigkeit des Handelsmarktes von Technologie zu. Das von Global Assets gestartete KI-intelligente Handelssystem integriert hochmoderne Technologien wie Big-Data-Analyse, maschinelles Lernen und Blockchain und verpflichtet sich, Benutzern intelligente und automatisierte Handelsdienste zu bieten, um menschliche Faktoren effektiv zu reduzieren.
 Warum ist der Anstieg oder Abfall der virtuellen Währungspreise? Warum ist der Anstieg oder Abfall der virtuellen Währungspreise?
Apr 21, 2025 am 08:57 AM
Warum ist der Anstieg oder Abfall der virtuellen Währungspreise? Warum ist der Anstieg oder Abfall der virtuellen Währungspreise?
Apr 21, 2025 am 08:57 AM
Faktoren der steigenden Preise für virtuelle Währung sind: 1. Erhöhte Marktnachfrage, 2. Verringertes Angebot, 3.. Rückgangsfaktoren umfassen: 1. Verringerte Marktnachfrage, 2. Erhöhtes Angebot, 3. Streik der negativen Nachrichten, 4. Pessimistische Marktstimmung, 5. makroökonomisches Umfeld.
 Der globale Markt für unkillbare Token hat den Neumond im April 2025 gesund und stark begonnen
Apr 20, 2025 pm 06:21 PM
Der globale Markt für unkillbare Token hat den Neumond im April 2025 gesund und stark begonnen
Apr 20, 2025 pm 06:21 PM
Defidungeons, eine NFT -Serie in einem von der Solana Blockchain betriebenen Fantasy Placement RPG -Spiel, zeigte Anfang April 2025 eine starke Marktleistung. Der globale NFT -Markt begann im April nach Wochen des Wachstums des Handelsvolumens stark. In den letzten 24 Stunden erreichte das gesamte NFT -Transaktionsvolumen 14 Millionen US -Dollar, wobei das Handelsvolumen gegenüber dem Vortag um 46% stieg. Hier sind die heißeste NFT-Serie in der ersten Aprilwoche: DefidungeonsNFT-Serie: Dieses Fantasy Placement RPG-Spiel NFT in der Solana-Blockchain wurde in der ersten Aprilwoche zur meistverkauften NFT-Serie. In den letzten 24 Stunden erreichte das Transaktionsvolumen 1,5 Millionen US -Dollar mit einem Gesamtmarktwert von mehr als 5 Millionen US -Dollar.
 Die Liste der Compliance -Lizenzen für die zehn Top -Blockchain -Börsen. Was sind die Plattformen für die strenge Aufsichtsauswahl?
Apr 21, 2025 am 08:12 AM
Die Liste der Compliance -Lizenzen für die zehn Top -Blockchain -Börsen. Was sind die Plattformen für die strenge Aufsichtsauswahl?
Apr 21, 2025 am 08:12 AM
Binance, OKX, Coinbase, Kraken, Huobi, Gate.io, Gemini, Xbit, Bitget und MEXC sind streng ausgewählte Plattformen für die regulatorische Auswahl. 1. Binance passt sich der Überwachung an, indem eine Compliance-Unterplattform eingerichtet wird. 2. OKX stärkt das Compliance -Management durch KYB -Überprüfung. 3.Coinbase ist bekannt für seine Einhaltung und Benutzerfreundlichkeit. 4.Kraken bietet leistungsstarke KYC- und Anti-Geldwäsche-Maßnahmen. 5. Huobi ist in Einklang mit dem asiatischen Markt. 6.Gate.io konzentriert sich auf die Sicherheit und Einhaltung der Transaktion. 7. Gemini konzentriert sich auf Sicherheit und Transparenz. 8.xbit ist ein Modell der dezentralen Transaktionskonformität. 9. Titget arbeitet weiterhin in Compliance -Operationen. 10.Mexc bestanden
 Machen Sie mit dem Tempo von Coinjie.com Schritt: Was ist die Investitionsaussicht auf Krypto -Finanz- und AAAS -Geschäft?
Apr 21, 2025 am 10:42 AM
Machen Sie mit dem Tempo von Coinjie.com Schritt: Was ist die Investitionsaussicht auf Krypto -Finanz- und AAAS -Geschäft?
Apr 21, 2025 am 10:42 AM
Die Investitionsaussichten von Unternehmen für Krypto -Finanz- und AAAS -Unternehmen werden wie folgt analysiert: 1. Möglichkeiten der Kryptofinanzierung umfassen Marktgrößenwachstum, schrittweise klare Regulierung und Erweiterung von Anwendungsszenarien, aber die Marktvolatilität und die technischen Sicherheitsherausforderungen gegenüberstehen. 2. Die Chancen des AAAS -Geschäfts liegen in der Förderung technologischer Innovationen, des Datenwerts und der reichhaltigen Anwendungsszenarien. Zu den Herausforderungen zählen jedoch die technische Komplexität und die Marktakzeptanz.
 Web3 Trading Platform Ranking_Web3 Globale Top Ten Summary Top Ten Summary
Apr 21, 2025 am 10:45 AM
Web3 Trading Platform Ranking_Web3 Globale Top Ten Summary Top Ten Summary
Apr 21, 2025 am 10:45 AM
Binance ist der Overlord des Global Digital Asset Trading -Ökosystems, und seine Merkmale umfassen: 1. Das durchschnittliche tägliche Handelsvolumen übersteigt 150 Milliarden US -Dollar, unterstützt 500 Handelspaare, die 98% der Mainstream -Währungen abdecken. 2. Die Innovationsmatrix deckt den Markt für Derivate, das Web3 -Layout und den Bildungssystem ab; 3. Die technischen Vorteile sind Millisekunden -Matching -Engines mit Spitzenvolumina von 1,4 Millionen Transaktionen pro Sekunde. 4. Compliance Progress hält 15 Länderlizenzen und legt konforme Einheiten in Europa und den Vereinigten Staaten ein.
 Binance Kernel Airdrop entsperren, neues Gameplay für BNB -Holding -Positionen
Apr 21, 2025 pm 01:06 PM
Binance Kernel Airdrop entsperren, neues Gameplay für BNB -Holding -Positionen
Apr 21, 2025 pm 01:06 PM
In der Flut der Kryptowährungen entstehen weiterhin neue Möglichkeiten und Projekte. Kürzlich hat das von Binance ins Leben gerufene Kerneldao (Kernel) -Projekt viel Aufmerksamkeit erregt und BNB -Inhabern neue Gameplay und Vorteile gebracht.



