 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Geschrieben im Vorfeld und nach persönlichem Verständnis des Autors
Dreidimensionales Gaußsches Splatting (3DGS) ist eine revolutionäre Technologie, die in den letzten Jahren in den Bereichen explizite Strahlungsfelder und Computergrafik entstanden ist. Diese innovative Methode zeichnet sich durch die Verwendung von Millionen von 3D-Gaußkurven aus, was sich stark von der Neural Radiation Field (NeRF)-Methode unterscheidet, die hauptsächlich ein implizites koordinatenbasiertes Modell verwendet, um räumliche Koordinaten auf Pixelwerte abzubilden. Mit seiner expliziten Szenendarstellung und differenzierbaren Rendering-Algorithmen garantiert 3D GS nicht nur Echtzeit-Rendering-Fähigkeiten, sondern führt auch ein beispielloses Maß an Kontrolle und Szenenbearbeitung ein. Dies positioniert 3D GS als potenziellen Game-Changer für die 3D-Rekonstruktion und -Darstellung der nächsten Generation. Zu diesem Zweck bieten wir erstmals einen systematischen Überblick über die neuesten Entwicklungen und Schlüsselbeiträge im Bereich 3D-GS. Zunächst werden die Grundprinzipien und Formeln für die Entstehung von 3D-GS im Detail untersucht und so die Grundlage für das Verständnis seiner Bedeutung gelegt. Anschließend wird ausführlich auf die Praktikabilität von 3D GS eingegangen. Durch die Erleichterung der Echtzeitleistung eröffnet 3D GS eine Vielzahl von Anwendungen, von virtueller Realität bis hin zu interaktiven Medien und mehr. Darüber hinaus wird eine vergleichende Analyse führender 3D-GS-Modelle durchgeführt und anhand verschiedener Benchmark-Aufgaben bewertet, um deren Leistung und Praktikabilität hervorzuheben. Der Bericht schließt mit der Identifizierung aktueller Herausforderungen und der Anregung potenzieller Wege für zukünftige Forschung in diesem Bereich. Mit dieser Umfrage möchten wir sowohl Neueinsteigern als auch erfahrenen Forschern eine wertvolle Ressource zur Verfügung stellen und die weitere Erforschung und Weiterentwicklung anwendbarer und eindeutiger Darstellungen von Strahlungsfeldern anregen.
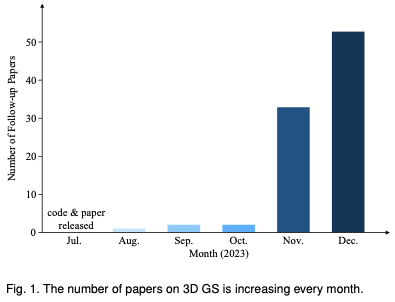
Um den Lesern zu helfen, mit der rasanten Entwicklung von 3D GS Schritt zu halten, stellen wir den ersten Umfragebericht zu 3D GS zur Verfügung. Wir haben systematisch und zeitnah die wichtigste aktuelle Literatur zu diesem Thema gesammelt, hauptsächlich von arxiv. Ziel dieses Artikels ist es, eine umfassende und aktuelle Analyse der anfänglichen Entwicklung, der theoretischen Grundlagen und der neuen Anwendungen von 3D GS bereitzustellen und dessen revolutionäres Potenzial auf diesem Gebiet hervorzuheben. Angesichts der noch jungen, aber sich schnell weiterentwickelnden Natur der 3D-GS zielt diese Umfrage auch darauf ab, aktuelle Herausforderungen und Zukunftsaussichten in diesem Bereich zu identifizieren und zu diskutieren. Wir bieten Einblicke in laufende Forschungsrichtungen und potenzielle Fortschritte, die 3D-GS ermöglichen könnte. Es ist zu hoffen, dass diese Übersicht nicht nur akademische Erkenntnisse liefert, sondern auch weitere Forschung und Innovation auf diesem Gebiet anregt. Der Aufbau dieses Artikels ist wie folgt: (Abbildung 2) Bitte beachten Sie, dass alle Inhalte auf der neuesten Literatur und Forschungsergebnissen basieren und darauf abzielen, den Lesern umfassende und zeitnahe Informationen über 3D GS zu bieten.
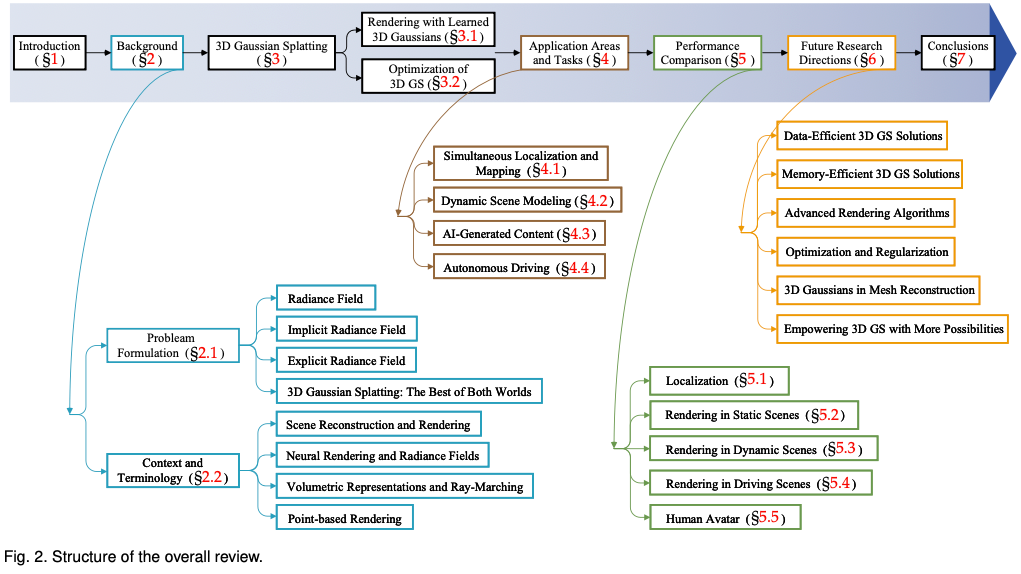
Einführung in den Hintergrund
In diesem Abschnitt wird die kurze Formel des Strahlungsfelds vorgestellt, die ein Schlüsselkonzept beim Rendern von Szenen darstellt. Strahlungsfelder können durch zwei Haupttypen dargestellt werden: implizit, wie NeRF, das neuronale Netze für die direkte, aber rechenintensive Darstellung verwendet, und explizit, wie Netze, die diskrete Strukturen für schnelleren Zugriff, aber weniger Speicherverbrauch verwenden; Als Nächstes werden wir die Verbindungen zu verwandten Bereichen wie Szenenrekonstruktion und -rendering weiter untersuchen.
Problemdefinition
Strahlungsfeld: Ein Strahlungsfeld ist eine Darstellung der Lichtverteilung im dreidimensionalen Raum, die erfasst, wie Licht mit Oberflächen und Materialien in der Umgebung interagiert. Mathematisch kann ein Strahlungsfeld als eine Funktion beschrieben werden, die einen Punkt im Raum und eine durch Kugelkoordinaten angegebene Richtung auf nichtnegative Strahlungswerte abbildet. Strahlungsfelder können durch implizite oder explizite Darstellungen gekapselt werden, von denen jede spezifische Szenendarstellungs- und Rendering-Vorteile bietet.
Implizites Strahlungsfeld: Ein implizites Strahlungsfeld repräsentiert die Lichtverteilung in einer Szene, ohne die Geometrie der Szene explizit zu definieren. Im Zeitalter des Deep Learning werden häufig neuronale Netze verwendet, um kontinuierliche volumetrische Szenendarstellungen zu lernen. Das prominenteste Beispiel ist NeRF. In NeRF wird ein MLP-Netzwerk verwendet, um einen Satz räumlicher Koordinaten und Blickrichtungen auf Farb- und Dichtewerte abzubilden. Die Strahldichte eines beliebigen Punktes wird nicht explizit gespeichert, sondern in Echtzeit durch Abfrage des neuronalen Netzwerks berechnet. Daher kann die Funktion wie folgt geschrieben werden:
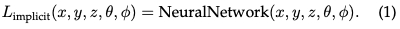
Dieses Format ermöglicht eine kompakte, differenzierbare Darstellung komplexer Szenen, allerdings mit einer höheren Rechenlast beim Rendern aufgrund der volumetrischen Strahlbewegung.
Explizite Strahlungsfelder: Im Gegensatz dazu repräsentieren explizite Strahlungsfelder direkt die Lichtverteilung in einer diskreten räumlichen Struktur, beispielsweise einem Voxelgitter oder einer Menge von Punkten. Jedes Element in der Struktur speichert Strahlungsinformationen für seine entsprechende Position im Raum. Dieser Ansatz ermöglicht einen direkteren und oft schnelleren Zugriff auf radiometrische Daten, allerdings auf Kosten einer höheren Speichernutzung und möglicherweise einer geringeren Auflösung. Die allgemeine Form der expliziten Strahlungsfelddarstellung kann wie folgt geschrieben werden:
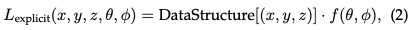
Wobei DataStructure ein Gitter oder eine Punktwolke sein kann, eine Funktion, die die Strahlung basierend auf der Blickrichtung modifiziert.
Das Beste aus beiden Welten: 3D-Gaußsches Splatting: 3D-GS stellt den Übergang von impliziten zu expliziten Strahlungsfeldern dar. Es nutzt die Vorteile beider Methoden, indem es 3D-Gaußfunktionen als flexible und effiziente Darstellung nutzt. Diese Gaußschen Koeffizienten sind optimiert, um die Szene genau darzustellen, und kombinieren die Vorteile der auf neuronalen Netzwerken basierenden Optimierung und der expliziten strukturierten Datenspeicherung. Dieser hybride Ansatz zielt darauf ab, ein qualitativ hochwertiges Rendering mit schnellerem Training und Echtzeitleistung zu erreichen, insbesondere für komplexe Szenen und hochauflösende Ausgaben. Die 3D-Gaußsche Darstellung wird wie folgt formuliert:
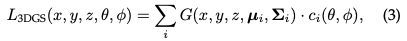
Kontext und Terminologie
Viele Technologien und Forschungsdisziplinen stehen in engem Zusammenhang mit 3D-GS, was im Folgenden kurz beschrieben wird.
Szenenrekonstruktion und -rendering: Grob gesagt umfasst die Szenenrekonstruktion die Erstellung eines 3D-Modells einer Szene aus einer Sammlung von Bildern oder anderen Daten. Rendering ist ein spezifischerer Begriff, der sich auf die Umwandlung computerlesbarer Informationen (z. B. 3D-Objekte in einer Szene) in pixelbasierte Bilder konzentriert. Frühe Techniken basierten auf Lichtfeldern, um realistische Bilder zu erzeugen. Structure-from-Motion- (SfM) und Multi-View-Stereo-Algorithmen (MVS) bringen das Gebiet weiter voran, indem sie die 3D-Struktur aus Bildsequenzen schätzen. Diese historischen Methoden legten den Grundstein für komplexere Techniken zur Szenenrekonstruktion und -wiedergabe.
Neuronales Rendering mit Strahlungsfeldern: Neural Rendering kombiniert Deep Learning mit traditionellen Grafiktechniken, um fotorealistische Bilder zu erstellen. Frühe Versuche nutzten Convolutional Neural Networks (CNNs), um Hybridgewichte oder Texturraumlösungen abzuschätzen. Ein Strahlungsfeld stellt eine Funktion dar, die die Lichtmenge beschreibt, die sich in jede Richtung durch jeden Punkt im Raum bewegt. NeRFs nutzt neuronale Netze zur Modellierung von Strahlungsfeldern und ermöglicht so eine detaillierte und realistische Szenendarstellung.
Volumendarstellung und Ray-Marching: Die Volumendarstellung modelliert Objekte und Szenen nicht nur als Oberflächen, sondern auch als mit Materialien oder leerem Raum gefüllte Volumina. Diese Methode ermöglicht eine genauere Darstellung von Phänomenen wie Nebel, Rauch oder durchscheinenden Materialien. Ray-Marching ist eine Technik, die bei volumetrischen Darstellungen zum Rendern von Bildern verwendet wird, indem der Weg des Lichts durch ein Volumen schrittweise verfolgt wird. NeRF teilt den gleichen Geist des volumetrischen Ray Marching und führt wichtige Abtastung und Positionskodierung ein, um die Qualität synthetisierter Bilder zu verbessern. Obwohl die Volumenstrahlbewegung qualitativ hochwertige Ergebnisse liefert, ist sie rechenintensiv, was die Suche nach effizienteren Methoden wie 3D-GS anregt.
Punktbasiertes Rendering: Punktbasiertes Rendering ist eine Technik zur Visualisierung von 3D-Szenen mithilfe von Punkten anstelle herkömmlicher Polygone. Dieser Ansatz ist besonders effektiv für die Darstellung komplexer, unstrukturierter oder spärlicher geometrischer Daten. Punkte können mit zusätzlichen Eigenschaften wie lernbaren neuronalen Deskriptoren erweitert und effizient gerendert werden. Bei diesem Ansatz können jedoch Probleme wie Lücken oder Aliasing-Effekte beim Rendering auftreten. 3D GS erweitert dieses Konzept durch die Verwendung anisotroper Gauß-Funktionen, um eine kontinuierlichere und zusammenhängendere Darstellung der Szene zu erreichen.
3D-Gauß für explizite Strahlungsfelder
3D GS ist ein Durchbruch in der Echtzeit-Bildwiedergabe mit hoher Auflösung, ohne auf neuronale Komponenten angewiesen zu sein.
Erlernte 3D-Gauß-Funktionen für eine neue Perspektivensynthese
Stellen Sie sich eine Szene vor, die durch (Millionen) optimierte 3D-Gauß-Funktionen dargestellt wird. Das Ziel besteht darin, ein Bild basierend auf einer bestimmten Kameraposition zu generieren. Denken Sie daran, dass NeRF diese Aufgabe erfüllt, indem es den volumetrischen Strahlweg rechentechnisch aufwändig macht und für jedes Pixel einen 3D-Raumpunkt abtastet. Dieser Modus macht es schwierig, eine hochauflösende Bildsynthese zu erreichen und kann keine Echtzeit-Rendering-Geschwindigkeit erreichen. Im krassen Gegensatz dazu projiziert 3D GS diese 3D-Gaußkurven zunächst auf eine pixelbasierte Bildebene, ein Vorgang, der als „Splatting“ bezeichnet wird (Abb. 3a). 3D GS sortiert dann diese Gaußschen Werte und berechnet den Wert jedes Pixels. Wie in der Abbildung gezeigt, kann das Rendern von NeRF und 3D GS als umgekehrter Prozess betrachtet werden. Im Folgenden beginnen wir mit der Definition eines 3D-Gauß-Werts, dem kleinsten Element der Szenendarstellung in einem 3D-GS. Als nächstes beschreiben wir, wie diese 3D-Gauß-Funktionen für differenzierbares Rendering verwendet werden. Schließlich wird die in 3D GS verwendete Beschleunigungstechnologie vorgestellt, die der Schlüssel zu schnellem Rendern ist.
Eigenschaften der dreidimensionalen Gaußschen Funktion: Die Eigenschaften der dreidimensionalen Gaußschen Funktion sind ihr Mittelpunkt (Position) μ, die Opazität α, die dreidimensionale Kovarianzmatrix ∑ und die Farbe c. Für ein ansichtsabhängiges Erscheinungsbild wird c durch die sphärischen Harmonischen dargestellt. Alle Attribute sind über Backpropagation lernbar und optimiert.
Frustum Culling: Anhand einer bestimmten Kameraposition bestimmt dieser Schritt, welche 3D-Gauß-Kurven außerhalb des Kegelstumpfs der Kamera liegen. Auf diese Weise werden 3D-Gauß-Funktionen außerhalb einer bestimmten Ansicht nicht in nachfolgende Berechnungen einbezogen, wodurch Rechenressourcen gespart werden.
Splatting: ** In diesem Schritt wird ein 3D-Gaußscher (Ellipsoid) zum Rendern in einen 2D-Bildraum (Ellipsoid) projiziert. Bei einer Betrachtungstransformation W und einer 3D-Kovarianzmatrix Σ wird die projizierte 2D-Kovarianzmatrix Σ′ mit der folgenden Formel berechnet:
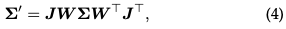
wobei J die Jacobi-Matrix der affinen Näherung der projektiven Transformation ist.
Pixel-Rendering: Bevor wir uns mit der endgültigen Version von 3D GS befassen, gehen wir zunächst auf die einfachere Form ein, um ein tieferes Verständnis für die Funktionsweise zu gewinnen. 3D GS nutzt mehrere Technologien, um paralleles Rechnen zu ermöglichen. Gegeben sei die Position eines Pixels Dann wird die Alpha-Synthese verwendet, um die endgültige Farbe für dieses Pixel zu berechnen:
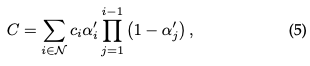
wobei die gelernte Farbe ist und die endgültige Deckkraft das Produkt aus der gelernten Deckkraft und dem Gaußschen Wert ist:
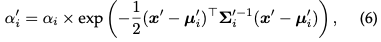
wobei x′ und μ sind die Koordinaten im projizierten Raum. Angesichts der Tatsache, dass die Generierung der erforderlichen sortierten Listen schwierig zu parallelisieren ist, kann der beschriebene Rendering-Prozess im Vergleich zu NeRF langsamer sein, was ein berechtigtes Problem darstellt. Tatsächlich ist diese Sorge berechtigt; die Rendering-Geschwindigkeit kann bei Verwendung dieses einfachen Pixel-für-Pixel-Ansatzes erheblich beeinträchtigt werden. Um Echtzeit-Rendering zu erreichen, hat 3DGS einige Zugeständnisse gemacht, um paralleles Rechnen zu ermöglichen.
Kacheln (Patches): Um den Rechenaufwand für die Ableitung von Gaußschen Koeffizienten für jedes Pixel zu vermeiden, überträgt 3D GS die Genauigkeit von der Pixelebene auf die Details auf Patchebene. Konkret unterteilt 3D GS das Bild zunächst in mehrere nicht überlappende Blöcke, im Originalpapier „Kacheln“ genannt. Abbildung 3b zeigt eine Darstellung der Kacheln. Jede Kachel besteht aus 16×16 Pixeln. 3D GS bestimmt außerdem, welche Kacheln diese projizierten Gaußschen Karten schneiden. Unter der Annahme, dass die projizierte Gaußsche Funktion mehrere Kacheln abdecken kann, besteht der logische Ansatz darin, die Gaußsche Funktion zu kopieren und jeder Kopie die Kennung der relevanten Kachel (d. h. Kachel-ID) zuzuweisen.
Paralleles Rendering: Nach dem Kopieren kombiniert 3D GS die einzelnen Kachel-IDs mit den Tiefenwerten, die aus der Ansichtstransformation jedes Gaußschen erhalten werden. Dies erzeugt eine unsortierte Liste von Bytes, wobei die höherwertigen Bits die Kachel-ID und die niederwertigen Bits die Tiefe darstellen. Auf diese Weise kann die sortierte Liste direkt zum Rendern (d. h. Alpha-Compositing) verwendet werden. Die Abbildungen 3c und 3d bieten visuelle Demonstrationen dieser Konzepte. Hervorzuheben ist, dass das Rendern jeder Kachel und jedes Pixels unabhängig erfolgt, was diesen Prozess ideal für paralleles Rechnen macht. Ein weiterer Vorteil besteht darin, dass die Pixel jeder Kachel Zugriff auf den gemeinsamen Speicher haben und eine einheitliche Lesesequenz beibehalten, wodurch Alpha-Compositing parallel und effizienter durchgeführt werden kann. In der offiziellen Implementierung des Originalpapiers behandelt das Framework die Verarbeitung von Kacheln bzw. Pixeln als ähnlich zu Blöcken und Threads in der CUDA-Programmierarchitektur.
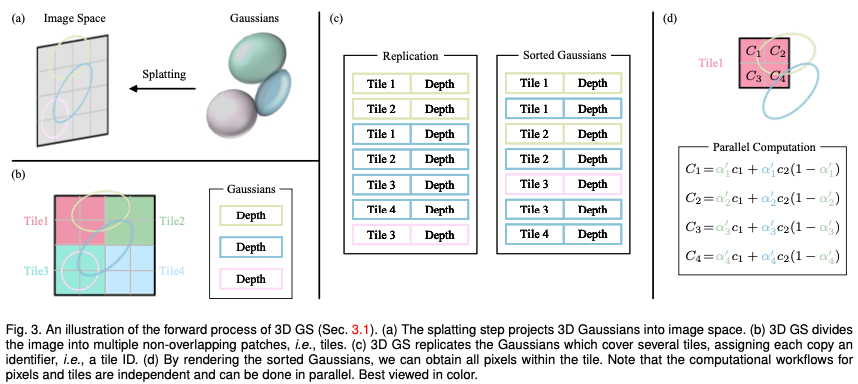
Kurz gesagt führt 3D GS mehrere Näherungen in der Vorwärtsverarbeitungsphase ein, um die Recheneffizienz zu verbessern und gleichzeitig einen hohen Standard der Bildsynthesequalität aufrechtzuerhalten.
Optimierung des 3D-Gaußschen Splattings
Der Kern von 3D GS ist ein Optimierungsprozess, der darauf ausgelegt ist, eine große Sammlung von 3D-Gaußschen zu erstellen, die das Wesentliche der Szene genau erfasst und so das Rendern aus freier Sicht ermöglicht. Einerseits sollten die Eigenschaften von 3D-Gaußschen durch differenzierbares Rendering optimiert werden, um sie an die Textur einer bestimmten Szene anzupassen. Andererseits ist die Anzahl der 3D-Gaußkurven, die eine bestimmte Szene gut darstellen können, nicht im Voraus bekannt. Ein vielversprechender Ansatz besteht darin, neuronale Netze automatisch 3D-Gaußsche Dichten erlernen zu lassen. Wir werden uns damit befassen, wie man die Eigenschaften jedes Gauß-Operators optimiert und wie man die Dichte der Gauß-Operatoren kontrolliert. Diese beiden Prozesse sind im Optimierungsworkflow verschachtelt. Da es während der Optimierung viele manuell eingestellte Hyperparameter gibt, lassen wir der Übersichtlichkeit halber die Symbole der meisten Hyperparameter weg.
Parameteroptimierung
Verlustfunktion: Sobald die Synthese des Bildes abgeschlossen ist, wird der Verlust als Differenz zwischen dem gerenderten Bild und der GT berechnet:
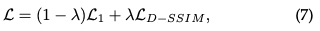
Die Verlustfunktion von 3D-GS ist etwas anders als bei NeRFs. Aufgrund des zeitaufwändigen Ray-Marching wird NeRF normalerweise auf Pixelebene und nicht auf Bildebene berechnet.
Parameteraktualisierung: Die meisten Eigenschaften von 3D-Gaußian können direkt durch Backpropagation optimiert werden. Es ist zu beachten, dass die direkte Optimierung der Kovarianzmatrix Σ zu einer nicht positiven semidefiniten Matrix führt, die nicht der physikalischen Interpretation entspricht, die normalerweise mit der Kovarianzmatrix verbunden ist. Um dieses Problem zu vermeiden, optimiert 3D GS das Quaternion q und den 3D-Vektor s. q und s stehen für Rotation bzw. Skalierung. Mit diesem Ansatz lässt sich die Kovarianzmatrix ∑ wie folgt rekonstruieren:

Dichtekontrolle
Initialisierung: 3D GS beginnt mit einem anfänglichen Satz von SfM oder zufällig initialisierten spärlichen Punkten. Anschließend werden Punktverdichtung und Beschneidung verwendet, um die Dichte der dreidimensionalen Gaußschen Kurven zu steuern.
Punktverdichtung: In der Punktverdichtungsphase erhöht 3D GS adaptiv die Gaußsche Dichte, um die Details der Szene besser zu erfassen. Bei diesem Verfahren wird besonders auf Bereiche geachtet, in denen geometrische Merkmale fehlen oder in denen die Gauß-Verteilung zu stark gestreut ist. Die Verdichtung wird nach einer bestimmten Anzahl von Iterationen durchgeführt und zielt auf Gaußsche Operatoren ab, die große Positionsgradienten im Sichtraum aufweisen (d. h. über einem bestimmten Schwellenwert). Dabei wird ein kleiner Gauß-Operator in unzureichend rekonstruierten Bereichen geklont oder ein großer Gauß-Operator in überrekonstruierten Bereichen gespalten. Beim Klonen wird eine Kopie des Gaußschen erstellt und in Richtung des Positionsgradienten verschoben. Bei der Aufteilung ersetzen zwei kleinere Gauß-Funktionen eine größere Gauß-Funktion und verringern so deren Größe um einen bestimmten Faktor. Dieser Schritt strebt die optimale Verteilung und Darstellung von Gaußschen im 3D-Raum an und verbessert dadurch die Gesamtqualität der Rekonstruktion.
Punktbereinigung: In der Punktbereinigungsphase werden redundante oder weniger einflussreiche Gaußsche Funktionen entfernt, was in gewissem Maße als Regularisierungsprozess angesehen werden kann. Dieser Schritt wird durchgeführt, indem nahezu transparente Gauß-Funktionen (α unter einem bestimmten Schwellenwert) und Gauß-Funktionen, die im Welt- oder Sichtraum zu groß sind, eliminiert werden. Um außerdem einen unangemessenen Anstieg der Gaußschen Dichte in der Nähe der Eingabekamera zu verhindern, wird der Alpha-Wert der Gaußschen Gleichungen nach einer bestimmten Anzahl von Iterationen nahe Null gesetzt. Dies ermöglicht die Steuerung der notwendigen Zunahme der Gaußschen Dichte und gleichzeitig die Eliminierung überschüssiger Gaußscher Teilchen. Dieser Prozess hilft nicht nur, Rechenressourcen zu sparen, sondern stellt auch sicher, dass die Darstellung der Szene durch die Gauß-Funktionen im Modell genau und effizient bleibt.
Anwendungsbereiche und Aufgaben
Das transformative Potenzial von 3D GS geht weit über seine theoretischen und rechnerischen Fortschritte hinaus. Dieser Abschnitt befasst sich mit verschiedenen bahnbrechenden Anwendungsbereichen, in denen 3D-GS erhebliche Auswirkungen hat, wie etwa Robotik, Szenenrekonstruktion und -darstellung, KI-generierte Inhalte, autonomes Fahren und sogar andere wissenschaftliche Disziplinen. Die Anwendung von 3D GS zeigt seine Vielseitigkeit und sein revolutionäres Potenzial. Hier skizzieren wir einige der bemerkenswertesten Anwendungsbereiche und geben einen Einblick, wie 3D GS in jedem Bereich neue Grenzen setzt.
SLAM
SLAM ist ein zentrales Rechenproblem für Robotik und autonome Systeme. Es besteht die Herausforderung für einen Roboter oder ein Gerät, seine Position in einer unbekannten Umgebung zu verstehen und gleichzeitig den Aufbau der Umgebung abzubilden. SLAM ist in einer Vielzahl von Anwendungen von entscheidender Bedeutung, darunter selbstfahrende Autos, Augmented Reality und Roboternavigation. Der Kern von SLAM besteht darin, eine Karte der unbekannten Umgebung zu erstellen und den Standort des Geräts auf der Karte in Echtzeit zu bestimmen. Daher stellt SLAM eine große Herausforderung für die rechenintensive Szenendarstellungstechnologie dar und ist auch eine gute Testumgebung für 3D-GS.
3D GS betritt das SLAM-Feld als innovative Methode zur Szenendarstellung. Herkömmliche SLAM-Systeme verwenden typischerweise Punkt-/Oberflächenwolken oder Voxelnetze, um die Umgebung darzustellen. Im Gegensatz dazu verwendet 3D GS anisotrope Gaußsche Werte, um die Umgebung besser darzustellen. Diese Darstellung bietet mehrere Vorteile: 1) Effizienz: Passen Sie die Dichte von 3D-Gaußkurven an, um räumliche Daten kompakt darzustellen und die Rechenlast zu reduzieren. 2) Genauigkeit: Anisotroper Gaußscher Modus ermöglicht eine detailliertere und genauere Umgebungsmodellierung, besonders geeignet für komplexe oder sich dynamisch ändernde Szenen. 3) Anpassungsfähigkeit: 3D GS kann sich an verschiedene Maßstäbe und komplexe Umgebungen anpassen und ist somit für verschiedene SLAM-Anwendungen geeignet. Mehrere innovative Studien haben 3D-Gaußsches Spritzen in SLAM verwendet und das Potenzial und die Vielseitigkeit dieses Paradigmas demonstriert.
Dynamische Szenenmodellierung
Dynamische Szenenmodellierung bezieht sich auf den Prozess der Erfassung und Darstellung der dreidimensionalen Struktur und des Erscheinungsbilds einer Szene, die sich im Laufe der Zeit ändert. Dazu gehört die Erstellung eines digitalen Modells, das die Geometrie, Bewegung und visuellen Aspekte der Objekte in der Szene genau wiedergibt. Die dynamische Szenenmodellierung ist in einer Vielzahl von Anwendungen von entscheidender Bedeutung, darunter virtuelle und erweiterte Realität, 3D-Animation und Computer Vision. 4D-Gaußsche Streuung (4D GS) erweitert das Konzept der 3D-GS auf dynamische Szenen. Es bezieht die zeitliche Dimension ein und ermöglicht die Darstellung und Wiedergabe von Szenen, die sich im Laufe der Zeit ändern. Dieses Paradigma bietet erhebliche Verbesserungen beim Rendern dynamischer Szenen in Echtzeit und sorgt gleichzeitig für eine hochwertige visuelle Ausgabe.
AIGC
AIGC bezieht sich auf digitale Inhalte, die durch Systeme der künstlichen Intelligenz autonom erstellt oder erheblich verändert werden, insbesondere in den Bereichen Computer Vision, Verarbeitung natürlicher Sprache und maschinelles Lernen. AIGC zeichnet sich durch seine Fähigkeit aus, künstlich generierte Inhalte zu simulieren, zu erweitern oder zu verbessern und ermöglicht so Anwendungen von der fotorealistischen Bildsynthese bis hin zur dynamischen narrativen Erstellung. Die Bedeutung von AIGC liegt in seinem transformativen Potenzial in verschiedenen Bereichen, darunter Unterhaltung, Bildung und technologische Entwicklung. Es ist ein Schlüsselelement in der sich entwickelnden Landschaft der Erstellung digitaler Inhalte und bietet eine skalierbare, anpassbare und oft effizientere Alternative zu herkömmlichen Methoden.
Diese eindeutige Funktion von 3D GS ermöglicht Echtzeit-Rendering-Funktionen und ein beispielloses Maß an Kontrolle und Bearbeitung, was es für AIGC-Anwendungen äußerst relevant macht. Die explizite Szenendarstellung und der differenzierbare Rendering-Algorithmus von 3D GS erfüllen vollständig die Anforderungen von AIGC an die Generierung von hochauflösenden, bearbeitbaren Echtzeitinhalten, die für Anwendungen in der virtuellen Realität, interaktiven Medien und anderen Bereichen von entscheidender Bedeutung sind.
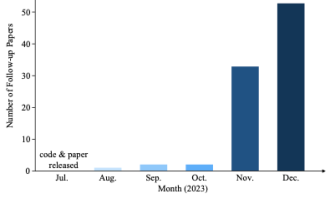
Autonomes Fahren
Autonomes Fahren soll es Fahrzeugen ermöglichen, ohne menschliches Eingreifen zu navigieren und zu funktionieren. Diese Fahrzeuge sind mit einer Reihe von Sensoren ausgestattet, darunter Kameras, LiDAR und Radar, kombiniert mit fortschrittlichen Algorithmen, Modellen für maschinelles Lernen und leistungsstarker Rechenleistung. Das zentrale Ziel besteht darin, die Umgebung zu erfassen, fundierte Entscheidungen zu treffen und Manöver sicher und effizient durchzuführen. Autonomes Fahren hat das Potenzial, das Transportwesen zu verändern und bietet entscheidende Vorteile wie die Verbesserung der Verkehrssicherheit durch die Reduzierung menschlicher Fehler, die Verbesserung der Mobilität für diejenigen, die nicht fahren können, und die Optimierung des Verkehrsflusses, wodurch Staus und Umweltbelastungen reduziert werden.
Autonome Fahrzeuge müssen die Umgebung erfassen und interpretieren, um sicher fahren zu können. Dazu gehört die Rekonstruktion von Fahrszenen in Echtzeit, die genaue Identifizierung statischer und dynamischer Objekte sowie das Verständnis ihrer räumlichen Beziehungen und Bewegungen. In dynamischen Fahrszenarien verändert sich die Umgebung ständig durch sich bewegende Objekte wie andere Fahrzeuge, Fußgänger oder Tiere. Die genaue Rekonstruktion dieser Szenen in Echtzeit ist für eine sichere Navigation von entscheidender Bedeutung, stellt jedoch aufgrund der Komplexität und Variabilität der beteiligten Elemente eine Herausforderung dar. Beim autonomen Fahren kann 3D GS zur Rekonstruktion von Szenen verwendet werden, indem Datenpunkte, wie sie beispielsweise von Sensoren wie LiDAR erhalten werden, zu einer zusammenhängenden und kontinuierlichen Darstellung zusammengeführt werden. Dies ist besonders nützlich, um unterschiedliche Dichten von Datenpunkten zu verarbeiten und eine reibungslose und genaue Rekonstruktion statischer Hintergründe und dynamischer Objekte in einer Szene sicherzustellen. Bisher gibt es nur wenige Arbeiten, die 3D-Gauß zur Modellierung dynamischer Fahr-/Straßenszenen verwenden und im Vergleich zu bestehenden Methoden eine hervorragende Leistung bei der Szenenrekonstruktion zeigen.
Leistungsvergleich
Dieser Abschnitt liefert weitere empirische Beweise, indem er die Leistung mehrerer 3D-GS-Algorithmen zeigt, die wir zuvor besprochen haben. Die vielfältigen Einsatzmöglichkeiten von 3D GS in vielen Aufgaben, gepaart mit dem individuellen Algorithmusdesign für jede Aufgabe, machen einen einheitlichen Vergleich aller 3D GS-Algorithmen innerhalb einer einzelnen Aufgabe oder eines einzelnen Datensatzes unpraktisch. Daher wählen wir drei repräsentative Aufgaben im 3D-GS-Bereich für eine eingehende Leistungsbewertung aus. Sofern nicht anders angegeben, basieren die Leistungen in erster Linie auf den Originalarbeiten.
Positionierungsleistung
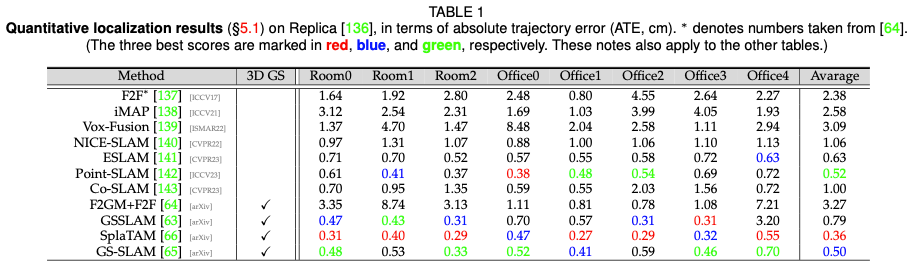
Digital Human Performance
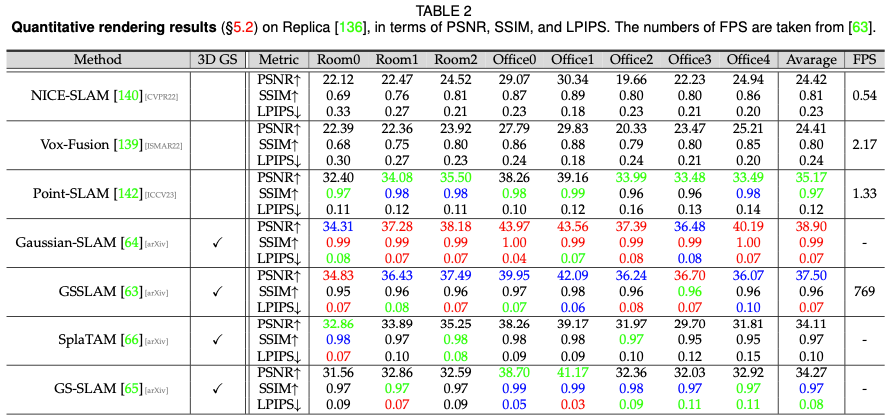
Zukünftige Forschungsrichtungen
Obwohl die Folgearbeiten zu 3D GS in den letzten Monaten erhebliche Fortschritte gemacht haben, glauben wir, dass es noch einige Herausforderungen gibt, die bewältigt werden müssen.- Dateneffiziente 3D-GS-Lösungen: Die Generierung neuartiger Ansichten und die Rekonstruktion von Szenen aus begrenzten Datenpunkten ist von großem Interesse, insbesondere da sie das Potenzial haben, den Realismus und die Benutzererfahrung mit minimalem Aufwand zu verbessern. Jüngste Fortschritte haben die Verwendung von Tiefeninformationen, dichten Wahrscheinlichkeitsverteilungen und einer Pixel-zu-Gauß-Abbildung untersucht, um diese Fähigkeit zu ermöglichen. Weitere Erkundungen in diesem Bereich sind jedoch weiterhin dringend erforderlich. Darüber hinaus ist ein wesentliches Problem der 3D-GS das Auftreten von Artefakten in Bereichen mit unzureichenden Beobachtungsdaten. Diese Herausforderung stellt eine häufige Einschränkung bei der Strahlungsfelddarstellung dar, da spärliche Daten häufig zu ungenauen Rekonstruktionen führen. Daher stellt die Entwicklung neuer Methoden zur Dateninterpolation oder -integration in diesen spärlichen Regionen einen vielversprechenden Weg für die zukünftige Forschung dar.
- Speichereffiziente 3D-GS-Lösung: Während 3D-GS außergewöhnliche Fähigkeiten aufweist, stellt seine Skalierbarkeit erhebliche Herausforderungen dar, insbesondere in Verbindung mit NeRF-basierten Ansätzen. Letzteres profitiert von der Einfachheit, nur die Parameter des gelernten MLP zu speichern. Dieses Skalierbarkeitsproblem wird im Zusammenhang mit der Verwaltung umfangreicher Szenen, bei denen der Rechen- und Speicherbedarf erheblich steigt, immer schwerwiegender. Daher besteht ein dringender Bedarf, die Speichernutzung während der Trainingsphase und die Modellspeicherung zu optimieren. Die Erforschung effizienterer Datenstrukturen und die Untersuchung fortschrittlicher Komprimierungstechniken sind vielversprechende Möglichkeiten, diese Einschränkungen zu beseitigen.
- Erweiterter Rendering-Algorithmus: Die aktuelle Rendering-Pipeline von 3D GS ist zukunftsorientiert und kann weiter optimiert werden. Beispielsweise kann ein einfacher Sichtbarkeitsalgorithmus zu einer drastischen Änderung der Gaußschen Tiefen-/Mischreihenfolge führen. Dies unterstreicht eine wichtige Chance für zukünftige Forschung: die Implementierung fortschrittlicherer Rendering-Algorithmen. Diese verbesserten Methoden sollten darauf abzielen, die komplexen Wechselwirkungen von Licht und Materialeigenschaften in einer bestimmten Szene genauer zu simulieren. Ein vielversprechender Ansatz könnte darin bestehen, etablierte Prinzipien der traditionellen Computergrafik zu assimilieren und an den spezifischen Kontext der 3D-GS anzupassen. Bemerkenswert in diesem Zusammenhang sind die laufenden Bemühungen, verbesserte Rendering-Techniken oder Hybridmodelle in den aktuellen Rechenrahmen von 3D GS zu integrieren. Darüber hinaus bietet die Erforschung des inversen Renderings und seiner Anwendungen einen fruchtbaren Boden für die Forschung.
- Optimierung und Regularisierung: Obwohl anisotrope Gauß-Funktionen zur Darstellung komplexer Geometrien nützlich sind, können sie visuelle Artefakte erzeugen. Beispielsweise können diese großen 3D-Gaußkurven, insbesondere in Bereichen mit ansichtsabhängigem Erscheinungsbild, Pop-in-Artefakte verursachen, bei denen visuelle Elemente plötzlich auftauchen oder verschwinden und so die Immersion unterbrechen. Es besteht erhebliches Forschungspotenzial in der Regularisierung und Optimierung von 3D-GS. Durch die Einführung von Anti-Aliasing können plötzliche Änderungen der Gaußschen Tiefe und der Mischreihenfolge abgemildert werden. Verbesserungen am Optimierungsalgorithmus können eine bessere Kontrolle über die Gaußschen Koeffizienten im Raum ermöglichen. Darüber hinaus kann die Einbeziehung der Regularisierung in den Optimierungsprozess die Konvergenz beschleunigen, visuelles Rauschen glätten oder die Bildqualität verbessern. Darüber hinaus wirkt sich eine so große Anzahl von Hyperparametern auf die Verallgemeinerung von 3D-GS aus, für die dringend Lösungen erforderlich sind.
- 3D-Gauß-Funktionen bei der Netzrekonstruktion: Das Potenzial von 3D-GS bei der Netzrekonstruktion und sein Platz im Spektrum der Volumen- und Oberflächendarstellungen müssen noch vollständig erforscht werden. Es besteht dringender Bedarf zu untersuchen, wie Gaußsche Grundelemente für Netzrekonstruktionsaufgaben geeignet sind. Diese Untersuchung könnte die Lücke zwischen volumetrischem Rendering und traditionellen oberflächenbasierten Methoden schließen und Einblicke in neue Rendering-Techniken und -Anwendungen liefern.
- Mehr Möglichkeiten für 3D-GS: Trotz des enormen Potenzials von 3D-GS bleibt das gesamte Anwendungsspektrum von 3D-GS weitgehend unerforscht. Eine vielversprechende Möglichkeit besteht darin, 3D-Gauß-Funktionen um zusätzliche Eigenschaften zu erweitern, beispielsweise sprachliche und physikalische Eigenschaften, die auf bestimmte Anwendungen zugeschnitten sind. Darüber hinaus haben neuere Forschungsarbeiten begonnen, die Fähigkeiten von 3D-GS in mehreren Bereichen aufzudecken, beispielsweise bei der Schätzung der Kameraposition, der Erfassung von Hand-Objekt-Interaktionen und der Quantifizierung von Unsicherheiten. Diese vorläufigen Ergebnisse bieten interdisziplinären Wissenschaftlern wichtige Möglichkeiten, 3D-GS weiter zu erforschen.
Fazit
Nach unserem Kenntnisstand bietet dieser Testbericht den ersten umfassenden Überblick über 3D GS, ein revolutionäres explizites Strahlungsfeld und Computergrafiktechnologie. Es stellt einen Paradigmenwechsel gegenüber herkömmlichen NeRF-Methoden dar und hebt die Vorteile von 3D GS beim Echtzeit-Rendering und der verbesserten Steuerbarkeit hervor. Unsere detaillierte Analyse zeigt die Vorteile von 3D GS in realen Anwendungen, insbesondere solchen, die Echtzeitleistung erfordern. Wir geben Einblicke in zukünftige Forschungsrichtungen und ungelöste Herausforderungen auf diesem Gebiet. Insgesamt handelt es sich bei 3D GS um eine transformative Technologie, von der erwartet wird, dass sie erhebliche Auswirkungen auf die zukünftige Entwicklung der 3D-Rekonstruktion und -Darstellung haben wird. Diese Umfrage soll als grundlegende Ressource dienen, um weitere Explorationen und Fortschritte in diesem sich schnell entwickelnden Bereich voranzutreiben.

Originallink: https://mp.weixin.qq.com/s/jH4g4Cx87nPUYN8iKaKcBA
Das obige ist der detaillierte Inhalt vonWarum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Jan 17, 2024 pm 02:57 PM
Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Jan 17, 2024 pm 02:57 PM
Oben geschrieben und persönliches Verständnis des Autors. Dreidimensionales Gaussplatting (3DGS) ist eine transformative Technologie, die in den letzten Jahren in den Bereichen explizite Strahlungsfelder und Computergrafik entstanden ist. Diese innovative Methode zeichnet sich durch die Verwendung von Millionen von 3D-Gaußkurven aus, was sich stark von der Neural Radiation Field (NeRF)-Methode unterscheidet, die hauptsächlich ein implizites koordinatenbasiertes Modell verwendet, um räumliche Koordinaten auf Pixelwerte abzubilden. Mit seiner expliziten Szenendarstellung und differenzierbaren Rendering-Algorithmen garantiert 3DGS nicht nur Echtzeit-Rendering-Fähigkeiten, sondern führt auch ein beispielloses Maß an Kontrolle und Szenenbearbeitung ein. Dies positioniert 3DGS als potenziellen Game-Changer für die 3D-Rekonstruktion und -Darstellung der nächsten Generation. Zu diesem Zweck geben wir erstmals einen systematischen Überblick über die neuesten Entwicklungen und Anliegen im Bereich 3DGS.
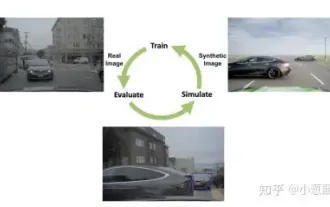 Wie lässt sich das Long-Tail-Problem in autonomen Fahrszenarien lösen?
Jun 02, 2024 pm 02:44 PM
Wie lässt sich das Long-Tail-Problem in autonomen Fahrszenarien lösen?
Jun 02, 2024 pm 02:44 PM
Gestern wurde ich während des Interviews gefragt, ob ich irgendwelche Long-Tail-Fragen gestellt hätte, also dachte ich, ich würde eine kurze Zusammenfassung geben. Das Long-Tail-Problem des autonomen Fahrens bezieht sich auf Randfälle bei autonomen Fahrzeugen, also mögliche Szenarien mit geringer Eintrittswahrscheinlichkeit. Das wahrgenommene Long-Tail-Problem ist einer der Hauptgründe, die derzeit den betrieblichen Designbereich intelligenter autonomer Einzelfahrzeugfahrzeuge einschränken. Die zugrunde liegende Architektur und die meisten technischen Probleme des autonomen Fahrens wurden gelöst, und die verbleibenden 5 % der Long-Tail-Probleme wurden nach und nach zum Schlüssel zur Einschränkung der Entwicklung des autonomen Fahrens. Zu diesen Problemen gehören eine Vielzahl fragmentierter Szenarien, Extremsituationen und unvorhersehbares menschliches Verhalten. Der „Long Tail“ von Randszenarien beim autonomen Fahren bezieht sich auf Randfälle in autonomen Fahrzeugen (AVs). Randfälle sind mögliche Szenarien mit geringer Eintrittswahrscheinlichkeit. diese seltenen Ereignisse
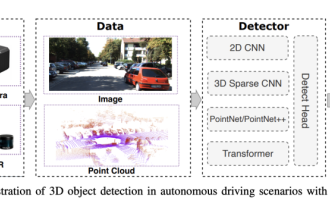 Kamera oder Lidar wählen? Eine aktuelle Übersicht über die Erzielung einer robusten 3D-Objekterkennung
Jan 26, 2024 am 11:18 AM
Kamera oder Lidar wählen? Eine aktuelle Übersicht über die Erzielung einer robusten 3D-Objekterkennung
Jan 26, 2024 am 11:18 AM
0. Vorab geschrieben&& Persönliches Verständnis, dass autonome Fahrsysteme auf fortschrittlichen Wahrnehmungs-, Entscheidungs- und Steuerungstechnologien beruhen, indem sie verschiedene Sensoren (wie Kameras, Lidar, Radar usw.) verwenden, um die Umgebung wahrzunehmen, und Algorithmen und Modelle verwenden für Echtzeitanalysen und Entscheidungsfindung. Dies ermöglicht es Fahrzeugen, Verkehrszeichen zu erkennen, andere Fahrzeuge zu erkennen und zu verfolgen, das Verhalten von Fußgängern vorherzusagen usw. und sich so sicher an komplexe Verkehrsumgebungen anzupassen. Diese Technologie erregt derzeit große Aufmerksamkeit und gilt als wichtiger Entwicklungsbereich für die Zukunft des Transportwesens . eins. Aber was autonomes Fahren schwierig macht, ist herauszufinden, wie man dem Auto klarmachen kann, was um es herum passiert. Dies erfordert, dass der dreidimensionale Objekterkennungsalgorithmus im autonomen Fahrsystem Objekte in der Umgebung, einschließlich ihrer Standorte, genau wahrnehmen und beschreiben kann.
 CLIP-BEVFormer: Überwacht explizit die BEVFormer-Struktur, um die Leistung der Long-Tail-Erkennung zu verbessern
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Überwacht explizit die BEVFormer-Struktur, um die Leistung der Long-Tail-Erkennung zu verbessern
Mar 26, 2024 pm 12:41 PM
Oben geschrieben und das persönliche Verständnis des Autors: Derzeit spielt das Wahrnehmungsmodul im gesamten autonomen Fahrsystem eine entscheidende Rolle Das Steuermodul im autonomen Fahrsystem trifft zeitnahe und korrekte Urteile und Verhaltensentscheidungen. Derzeit sind Autos mit autonomen Fahrfunktionen in der Regel mit einer Vielzahl von Dateninformationssensoren ausgestattet, darunter Rundumsichtkamerasensoren, Lidar-Sensoren und Millimeterwellenradarsensoren, um Informationen in verschiedenen Modalitäten zu sammeln und so genaue Wahrnehmungsaufgaben zu erfüllen. Der auf reinem Sehen basierende BEV-Wahrnehmungsalgorithmus wird von der Industrie aufgrund seiner geringen Hardwarekosten und einfachen Bereitstellung bevorzugt, und seine Ausgabeergebnisse können problemlos auf verschiedene nachgelagerte Aufgaben angewendet werden.
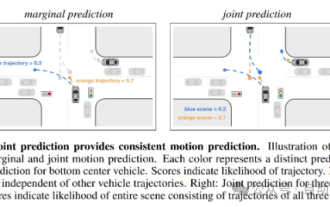 Dieser Artikel reicht aus, um etwas über autonomes Fahren und Flugbahnvorhersage zu lesen!
Feb 28, 2024 pm 07:20 PM
Dieser Artikel reicht aus, um etwas über autonomes Fahren und Flugbahnvorhersage zu lesen!
Feb 28, 2024 pm 07:20 PM
Die Trajektorienvorhersage spielt eine wichtige Rolle beim autonomen Fahren. Unter autonomer Fahrtrajektorienvorhersage versteht man die Vorhersage der zukünftigen Fahrtrajektorie des Fahrzeugs durch die Analyse verschiedener Daten während des Fahrvorgangs. Als Kernmodul des autonomen Fahrens ist die Qualität der Trajektorienvorhersage von entscheidender Bedeutung für die nachgelagerte Planungssteuerung. Die Trajektorienvorhersageaufgabe verfügt über einen umfangreichen Technologie-Stack und erfordert Vertrautheit mit der dynamischen/statischen Wahrnehmung des autonomen Fahrens, hochpräzisen Karten, Fahrspurlinien, Fähigkeiten in der neuronalen Netzwerkarchitektur (CNN&GNN&Transformer) usw. Der Einstieg ist sehr schwierig! Viele Fans hoffen, so schnell wie möglich mit der Flugbahnvorhersage beginnen zu können und Fallstricke zu vermeiden. Heute werde ich eine Bestandsaufnahme einiger häufiger Probleme und einführender Lernmethoden für die Flugbahnvorhersage machen! Einführungsbezogenes Wissen 1. Sind die Vorschaupapiere in Ordnung? A: Schauen Sie sich zuerst die Umfrage an, S
 SIMPL: Ein einfacher und effizienter Multi-Agent-Benchmark zur Bewegungsvorhersage für autonomes Fahren
Feb 20, 2024 am 11:48 AM
SIMPL: Ein einfacher und effizienter Multi-Agent-Benchmark zur Bewegungsvorhersage für autonomes Fahren
Feb 20, 2024 am 11:48 AM
Originaltitel: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Paper-Link: https://arxiv.org/pdf/2402.02519.pdf Code-Link: https://github.com/HKUST-Aerial-Robotics/SIMPL Autor: Hong Kong University of Science und Technologie DJI-Papieridee: Dieses Papier schlägt eine einfache und effiziente Bewegungsvorhersagebasislinie (SIMPL) für autonome Fahrzeuge vor. Im Vergleich zum herkömmlichen Agent-Cent
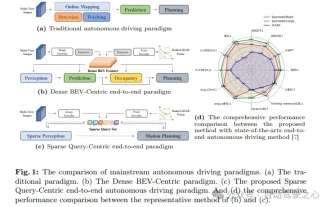 nuScenes' neuestes SOTA |. SparseAD: Sparse-Abfrage hilft effizientes durchgängiges autonomes Fahren!
Apr 17, 2024 pm 06:22 PM
nuScenes' neuestes SOTA |. SparseAD: Sparse-Abfrage hilft effizientes durchgängiges autonomes Fahren!
Apr 17, 2024 pm 06:22 PM
Vorab geschrieben und Ausgangspunkt Das End-to-End-Paradigma verwendet ein einheitliches Framework, um Multitasking in autonomen Fahrsystemen zu erreichen. Trotz der Einfachheit und Klarheit dieses Paradigmas bleibt die Leistung von End-to-End-Methoden für das autonome Fahren bei Teilaufgaben immer noch weit hinter Methoden für einzelne Aufgaben zurück. Gleichzeitig erschweren die in früheren End-to-End-Methoden weit verbreiteten Funktionen der dichten Vogelperspektive (BEV) die Skalierung auf mehr Modalitäten oder Aufgaben. Hier wird ein Sparse-Search-zentriertes End-to-End-Paradigma für autonomes Fahren (SparseAD) vorgeschlagen, bei dem die Sparse-Suche das gesamte Fahrszenario, einschließlich Raum, Zeit und Aufgaben, ohne dichte BEV-Darstellung vollständig abbildet. Insbesondere ist eine einheitliche, spärliche Architektur für die Aufgabenerkennung einschließlich Erkennung, Verfolgung und Online-Zuordnung konzipiert. Zudem schwer
 Sprechen wir über End-to-End- und autonome Fahrsysteme der nächsten Generation sowie über einige Missverständnisse über End-to-End-Autonomes Fahren?
Apr 15, 2024 pm 04:13 PM
Sprechen wir über End-to-End- und autonome Fahrsysteme der nächsten Generation sowie über einige Missverständnisse über End-to-End-Autonomes Fahren?
Apr 15, 2024 pm 04:13 PM
Im vergangenen Monat hatte ich aus bekannten Gründen einen sehr intensiven Austausch mit verschiedenen Lehrern und Mitschülern der Branche. Ein unvermeidliches Thema im Austausch ist natürlich End-to-End und der beliebte Tesla FSDV12. Ich möchte diese Gelegenheit nutzen, einige meiner aktuellen Gedanken und Meinungen als Referenz und Diskussion darzulegen. Wie definiert man ein durchgängiges autonomes Fahrsystem und welche Probleme sollten voraussichtlich durchgängig gelöst werden? Gemäß der traditionellsten Definition bezieht sich ein End-to-End-System auf ein System, das Rohinformationen von Sensoren eingibt und für die Aufgabe relevante Variablen direkt ausgibt. Bei der Bilderkennung kann CNN beispielsweise als End-to-End bezeichnet werden, verglichen mit der herkömmlichen Methode zum Extrahieren von Merkmalen + Klassifizieren. Bei autonomen Fahraufgaben werden Eingabedaten verschiedener Sensoren (Kamera/LiDAR) benötigt



