 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Deep Learning erreicht geniale Leistungen im geometrischen Denken. Nature veröffentlicht das DeepMind-Modell und erhält Lob in den Nachrichten über den Gewinner der Fields-Medaille
Deep Learning erreicht geniale Leistungen im geometrischen Denken. Nature veröffentlicht das DeepMind-Modell und erhält Lob in den Nachrichten über den Gewinner der Fields-Medaille
Deep Learning erreicht geniale Leistungen im geometrischen Denken. Nature veröffentlicht das DeepMind-Modell und erhält Lob in den Nachrichten über den Gewinner der Fields-Medaille
Diese Arbeit stellt einen Durchbruch in den mathematischen Denkfähigkeiten der KI dar und ist ein wichtiger Meilenstein in der Entwicklung allgemeiner KI-Systeme.
Dieses Mal gelang dem Algorithmus der künstlichen Intelligenz ein großer Durchbruch bei der Mathematikolympiade (IMO).
In der neuesten Ausgabe der international renommierten Fachzeitschrift „Nature“ wurde ein Artikel veröffentlicht, der ein künstliches Intelligenzsystem namens AlphaGeometry vorstellt. Das System ist in der Lage, olympische Geometrieprobleme ohne menschliches Zutun zu lösen. Experten glauben, dass dies ein wichtiger Meilenstein auf dem Weg der künstlichen Intelligenz hin zu menschlichen Denkfähigkeiten ist. Die Veröffentlichung dieses Forschungsergebnisses ist von großer Bedeutung für die Weiterentwicklung der Künstlichen Intelligenz.

Link zum Papier: https://www.nature.com/articles/s41586-023-06747-5
DeepMind hat auch den Code und das Modell als Open Source bereitgestellt, sobald das Papier veröffentlicht wurde, GitHub: https: // github.com/google-deepmind/alphageometry
Dies ist ein künstliches Intelligenzsystem von Google DeepMind-Forschern, das komplexe geometrische Probleme auf einem Niveau lösen kann, das dem der menschlichen Olympia-Goldmedaillengewinner nahekommt.
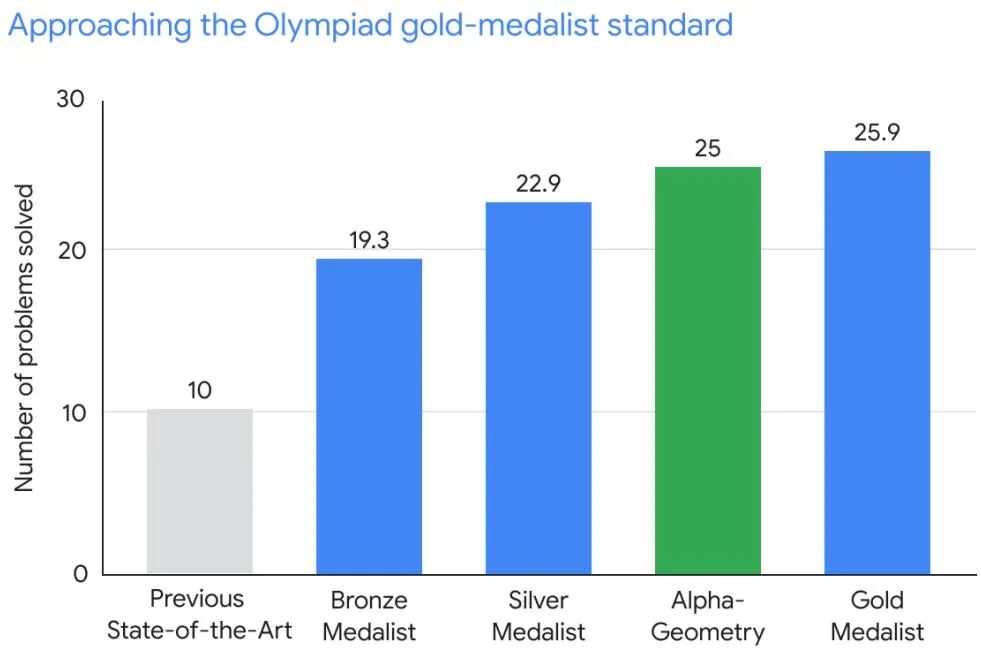
In einem Benchmark-Test mit 30 Geometriefragen der Mathematikolympiade löste AlphaGeometry 25 der Geometriefragen innerhalb des Standardzeitlimits der Mathematikolympiade, während das vorherige hochmoderne System nur 10 der Geometriefragen löste. Im Vergleich dazu lösten menschliche Goldmedaillengewinner durchschnittlich 25,9 Probleme.
Theorembeweis ist eine herausfordernde Aufgabe für lernbasierte KI-Modelle. Der Hauptgrund dafür ist, dass menschliche Beweise in den meisten mathematischen Bereichen schwer in maschinenüberprüfbare Sprache zu übersetzen sind, wodurch die Datenmenge begrenzt ist, die zum Trainieren von KI-Modellen verwendet wird. Um dieses Problem zu lösen, schlägt DeepMind eine alternative Methode zur Verwendung synthetischer Daten zum Beweisen von Theoremen vor. Sie entwickelten ein allgemeines Leitsystem namens AlphaGeometry, das in vielen Bereichen anwendbar ist. Durch die Nutzung synthetischer Daten ist AlphaGeometry in der Lage, KI-Modelle für die Beweisführung von Theoremen zu trainieren und qualitativ hochwertige Ergebnisse zu liefern. Diese Methode bietet eine wirksame Lösung für die Schwierigkeit des Theorembeweises.
Einführung in die Forschung
AlphaGeometry kombiniert Sprachmodelle mit „symbolischen Motoren“, um mithilfe von Symbolen und logischen Regeln mathematische Schlussfolgerungen durchzuführen. Unter anderem ist das Sprachmodell gut darin, die nachfolgenden Schritte des Prozesses zu identifizieren und vorherzusagen, aber es fehlt ihm an der für mathematisches Denken erforderlichen Genauigkeit. Andererseits basiert die symbolische Engine ausschließlich auf formaler Logik und strengen Regeln ermöglicht es, das Sprachmodell zu einer rationalen Entscheidungsfindung zu führen.
Im Rahmen der Forschung von AlphaGeometry führte DeepMind Tests aus dem Benchmark-Testsatz von 30 olympischen Geometrieproblemen (IMO-AG-30) im Zeitraum 2000 bis 2022 durch. Die Ergebnisse zeigten, dass AlphaGeometry das Problem innerhalb der Wettbewerbsfrist von 25 Fragen lösen kann . Die vorherige hochmoderne Methode (Wus Methode) konnte nur 10 lösen.
Es ist bekannt, dass KI-Systeme aufgrund mangelnder Denkfähigkeiten und Trainingsdaten oft Schwierigkeiten haben, komplexe Probleme in Geometrie und Mathematik zu lösen. Das AlphaGeometry-System kombiniert die Vorhersagekraft neuronaler Sprachmodelle mit einer regelbeschränkten Inferenzmaschine, die zusammenarbeiten, um neue Lösungen zu finden.
Um die Datenherausforderung zu bewältigen, generierte die Studie außerdem eine große Menge synthetischer Trainingsdaten, d. h. 100 Millionen Beispiele, in denen die Beweise vieler Theoreme mehr als 200 Schritte erfordern, was viermal länger ist als die durchschnittliche Beweislänge von Theoreme der Mathematischen Olympiade.
AlphaGeometry demonstriert die wachsenden Fähigkeiten der KI zum logischen Denken und die Fähigkeit, neues Wissen zu entdecken und zu verifizieren. Die Lösung von Geometrieproblemen auf olympischem Niveau ist ein wichtiger Meilenstein für die KI auf dem Weg zu fortschrittlicheren und allgemeineren Systemen der künstlichen Intelligenz.
Fields-Medaillengewinner und IMO-Goldmedaillengewinner Ngô Bảo Châu sagte: „Jetzt verstehe ich vollkommen, warum KI-Forscher zuerst versuchen, die Geometrieprobleme der Internationalen Mathematikolympiade (IMO) zu lösen, denn sie zu finden Die Lösung ist ein bisschen wie Schachspielen, Wir haben bei jedem Umzug relativ wenige vernünftige Schritte, aber ich bin immer noch schockiert, dass sie das geschafft haben

Wu Baozhu, Gewinner der Fields-Medaille 2010, ist derzeit Professor an der University of Chicago.
AlphaGeometry ist ein neurosymbolisches System, das aus einem neuronalen Sprachmodell und einer symbolischen Deduktionsmaschine besteht, die zusammenarbeiten, um Beweise für komplexe geometrische Theoreme zu finden. Ein System liefert schnelle, intuitive Ideen, während das andere durchdachtere, rationalere Entscheidungen ermöglicht.
Da Sprachmodelle gut darin sind, allgemeine Muster und Beziehungen in Daten zu identifizieren, können sie potenziell nützliche Strukturen schnell vorhersagen, aber oft mangelt es ihnen an schlüssiger Begründung oder Interpretation. Die symbolische Deduktionsmaschine hingegen basiert auf formaler Logik und verwendet explizite Regeln, um Schlussfolgerungen zu ziehen, die zusammen AlphaGeometry bilden. Das Sprachmodell von
AlphaGeometry steuert seine symbolische Deduktionsmaschine, um mögliche Lösungen für geometrische Probleme zu finden. Allgemeine Olympiade-Geometrieprobleme basieren auf Diagrammen und erfordern zur Lösung das Hinzufügen neuer geometrischer Strukturen wie Punkte, Linien oder Kreise. Das Sprachmodell von AlphaGeometry kann vorhersagen, welche neuen Strukturen aus unzähligen Möglichkeiten am sinnvollsten hinzuzufügen wären. Diese Hinweise helfen, die Lücken zu schließen und ermöglichen es der symbolischen Engine, weitere Rückschlüsse auf das Diagramm zu ziehen und einer Lösung näher zu kommen.
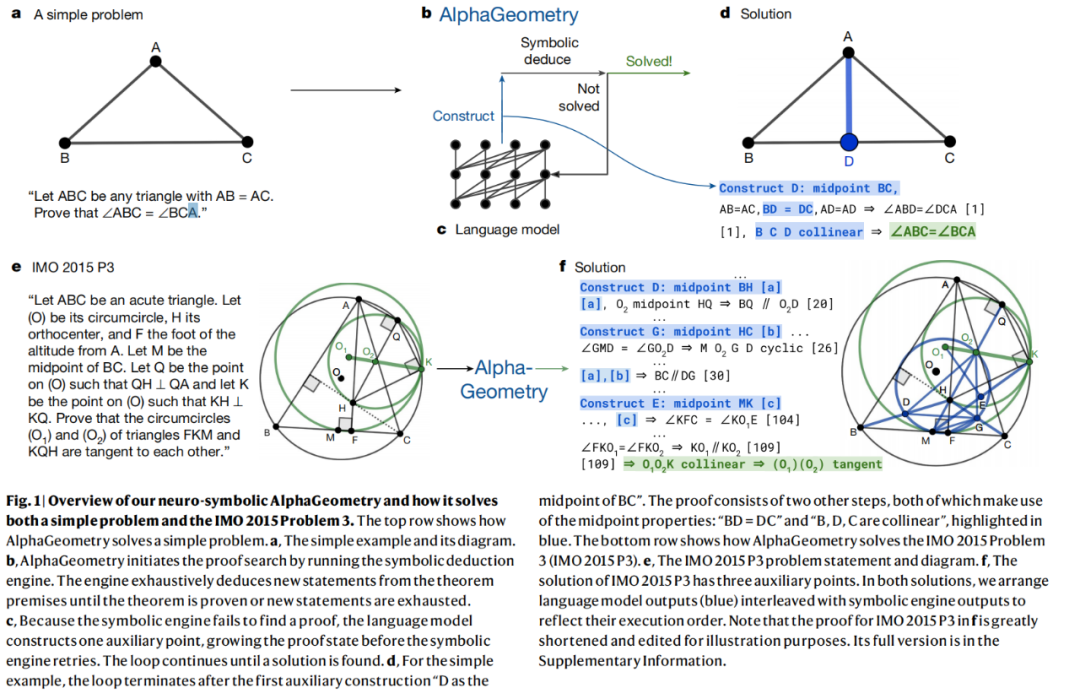
Das Bild unten (oben) zeigt beispielsweise den Prozess der Lösung einer einfachen Frage durch AlphaGeometry. Die Frage lautet: „Es sei ABC ein beliebiges Dreieck mit AB = AC. Beweisen Sie, dass ∠ABC = ∠BCA.“
AlphaGeometry Der Beweisprozess lautet wie folgt: AlphaGeometry Starten Sie die Beweissuche, indem Sie die symbolische Deduktionsmaschine ausführen. Diese Engine geht von den Prämissen des Satzes aus und leitet erschöpfend neue Aussagen ab, bis der Satz bewiesen ist oder die neuen Aussagen erschöpft sind. Wenn die symbolische Engine keinen Beweis findet, erstellt das Sprachmodell einen Hilfspunkt, der beweisbare Bedingungen hinzufügt, bevor die symbolische Engine neu startet. Dieser Zyklus wird fortgesetzt, bis eine Lösung gefunden ist. Für das einfache Beispiel endet die Schleife nach der ersten Hilfsstruktur „Füge Punkt D zum Mittelpunkt von BC hinzu“.
Das Bild unten (unten) zeigt die Lösung von AlphaGeometry für das IMO-Problem. „Beweisen Sie, dass die Umkreise (O1) und (O2) der Dreiecke FKM und KQH einander tangential sind …“ AlphaGeometry kann auch ein solch komplexes Problem beweisen, und der Beweisprozess liefert auch Hilfspunkte usw. Der Beweis wurde zur Veranschaulichung stark gekürzt und bearbeitet.
Generieren von 100 Millionen mathematischen Inferenz-Trainingsdaten
Menschen können Geometrie lernen, indem sie auf Papier skizzieren, Diagramme untersuchen und vorhandenes Wissen nutzen, um neue, komplexere geometrische Eigenschaften und Beziehungen zu entdecken. Der Ansatz dieser Studie zur Generierung synthetischer Daten simuliert diesen Wissensaufbauprozess im großen Maßstab. Die Methode zur Generierung synthetischer Daten ist in Abbildung 3 dargestellt.
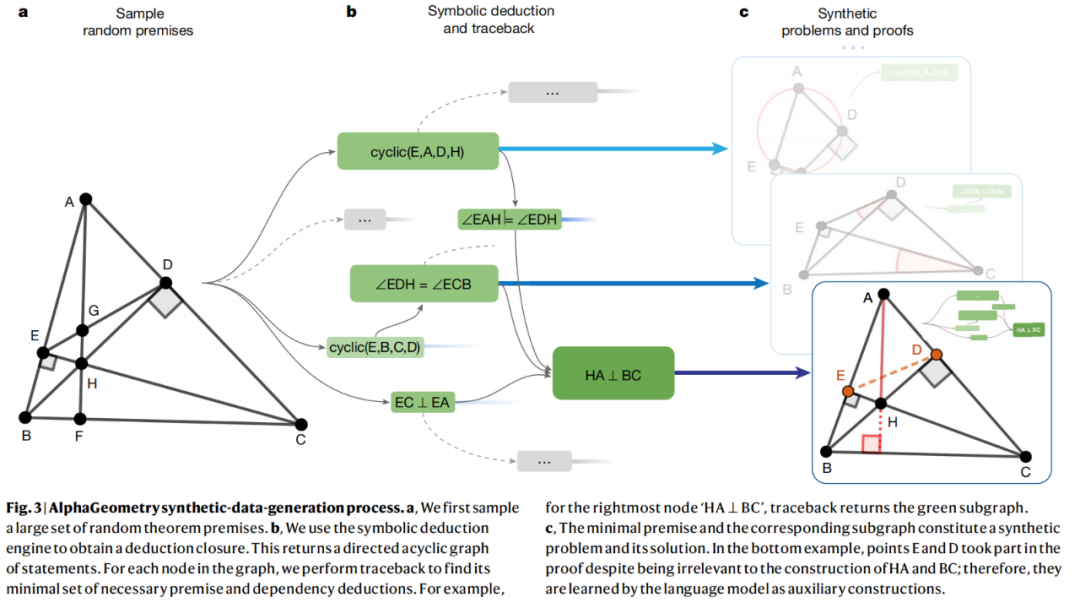
Mit hochparallelem Rechnen generiert das System zunächst zufällige Diagramme von 500 Millionen geometrischen Objekten und leitet alle Beziehungen zwischen Punkten und Linien in jedem Diagramm vollständig ab. AlphaGeometry findet alle in jedem Diagramm enthaltenen Beweise und arbeitet dann rückwärts, um herauszufinden, welche zusätzliche Struktur (falls vorhanden) erforderlich ist, um diese Beweise zu erhalten. Dieser Prozess ist „Symboldeduktion und Rückblick“.
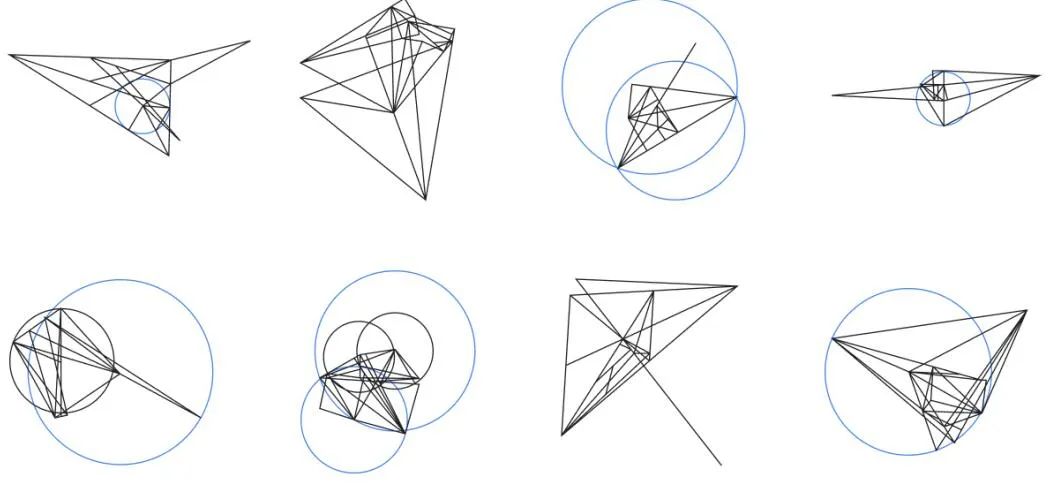
Visuelle Darstellung synthetischer Daten, die von AlphaGeometry generiert wurden
Anschließend wurde dieser riesige Datenpool gefiltert, um ähnliche Beispiele auszuschließen, was zu 100 Millionen Trainingsdatensätzen führte.
Wegweisende Denkfähigkeiten der künstlichen Intelligenz
Jede von AlphaGeometry bereitgestellte Lösung wurde von Computern überprüft und verifiziert. Die Forscher verglichen ihre Ergebnisse auch mit früheren Methoden der künstlichen Intelligenz und der menschlichen Leistung bei olympischen Wettkämpfen. Darüber hinaus evaluiert der Mathematiktrainer und ehemalige Olympia-Goldmedaillengewinner Evan Chen eine Reihe von AlphaGeometry-Lösungen für uns.

Chen Yiting, ein Doktorand in Mathematik am MIT, gewann die IMO 2014-Goldmedaille.
Evan Chen sagte: „Die Ausgabe von AlphaGeometry ist beeindruckend, weil sie sowohl überprüfbar als auch sauber ist. Frühere KI-Lösungen für beweisbasierte Wettbewerbsprobleme waren manchmal ein Zufall (die Ausgabe war manchmal korrekt und erforderte eine menschliche Überprüfung). AlphaGeometry hat diese Schwäche nicht: Seine Lösung hat eine maschinenüberprüfbare Struktur. Andererseits kann man sich ein Computerprogramm vorstellen, das geometrische Probleme durch Brute-Force-Koordinatensysteme löst und Seiten langwieriger algebraischer Berechnungen, AlphaGeometry macht das nicht, es verwendet klassische Geometrieregeln mit Winkeln und ähnlichen Dreiecken, wie es ein menschlicher Schüler tun würde
Kürzlich hat das Finanztechnologieunternehmen XTX Markets die Mathematische Olympiade für künstliche Intelligenz (AI-MO-Preis) ins Leben gerufen, um die Entwicklung von Modellen für künstliche Intelligenz zu fördern, die mathematisches Denken durchführen können. Da jede Olympiade sechs Probleme hat, von denen sich normalerweise nur zwei auf die Geometrie konzentrieren, kann AlphaGeometry nur auf ein Drittel der Probleme einer bestimmten Olympiade angewendet werden.
Trotzdem war AlphaGeometry das erste künstliche Intelligenzmodell der Welt, das in den Jahren 2000 und 2015 die IMO-Bronzemedaillenschwelle überschritt und sich dabei ausschließlich auf seine Fähigkeiten zur geometrischen Problemlösung verließ.
DeepMind arbeitet bereits daran, die Inferenz für Systeme der nächsten Generation künstlicher Intelligenz voranzutreiben. Die Forscher glauben, dass dieser Ansatz angesichts des breiten Potenzials der Nutzung umfangreicher synthetischer Daten zum Training von KI-Systemen von Grund auf die Richtung beeinflussen könnte, in der zukünftige KI-Systeme neues Wissen in der Mathematik und anderen Bereichen entdecken.
AlphaGeometry leistet Pionierarbeit beim mathematischen Denken in der künstlichen Intelligenz – von der Erforschung der Schönheit der reinen Mathematik bis hin zur Verwendung von Sprachmodellen zur Lösung mathematischer und wissenschaftlicher Probleme. Es besteht die Hoffnung, dass sich diese Technologie weiter verbessert, um komplexere, abstraktere mathematische Probleme zu lösen.
Neben der Mathematik kann die Wirkung von AlphaGeometry auch weitere Bereiche abdecken, darunter geometrische Probleme wie Computer Vision, Architektur und sogar theoretische Physik.
Referenzinhalt:
https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry/
Das obige ist der detaillierte Inhalt vonDeep Learning erreicht geniale Leistungen im geometrischen Denken. Nature veröffentlicht das DeepMind-Modell und erhält Lob in den Nachrichten über den Gewinner der Fields-Medaille. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Der DeepMind-Roboter spielt Tischtennis und seine Vor- und Rückhand rutschen in die Luft, wodurch menschliche Anfänger völlig besiegt werden
Aug 09, 2024 pm 04:01 PM
Der DeepMind-Roboter spielt Tischtennis und seine Vor- und Rückhand rutschen in die Luft, wodurch menschliche Anfänger völlig besiegt werden
Aug 09, 2024 pm 04:01 PM
Aber vielleicht kann er den alten Mann im Park nicht besiegen? Die Olympischen Spiele in Paris sind in vollem Gange und Tischtennis hat viel Aufmerksamkeit erregt. Gleichzeitig haben Roboter auch beim Tischtennisspielen neue Durchbrüche erzielt. Gerade hat DeepMind den ersten lernenden Roboteragenten vorgeschlagen, der das Niveau menschlicher Amateurspieler im Tischtennis-Wettkampf erreichen kann. Papieradresse: https://arxiv.org/pdf/2408.03906 Wie gut ist der DeepMind-Roboter beim Tischtennisspielen? Vermutlich auf Augenhöhe mit menschlichen Amateurspielern: Sowohl Vorhand als auch Rückhand: Der Gegner nutzt unterschiedliche Spielstile, und auch der Roboter hält aus: Aufschlagannahme mit unterschiedlichem Spin: Allerdings scheint die Intensität des Spiels nicht so intensiv zu sein wie Der alte Mann im Park. Für Roboter, Tischtennis
 Die erste mechanische Klaue! Yuanluobao trat auf der Weltroboterkonferenz 2024 auf und stellte den ersten Schachroboter vor, der das Haus betreten kann
Aug 21, 2024 pm 07:33 PM
Die erste mechanische Klaue! Yuanluobao trat auf der Weltroboterkonferenz 2024 auf und stellte den ersten Schachroboter vor, der das Haus betreten kann
Aug 21, 2024 pm 07:33 PM
Am 21. August fand in Peking die Weltroboterkonferenz 2024 im großen Stil statt. Die Heimrobotermarke „Yuanluobot SenseRobot“ von SenseTime hat ihre gesamte Produktfamilie vorgestellt und kürzlich den Yuanluobot AI-Schachspielroboter – Chess Professional Edition (im Folgenden als „Yuanluobot SenseRobot“ bezeichnet) herausgebracht und ist damit der weltweit erste A-Schachroboter für heim. Als drittes schachspielendes Roboterprodukt von Yuanluobo hat der neue Guoxiang-Roboter eine Vielzahl spezieller technischer Verbesserungen und Innovationen in den Bereichen KI und Maschinenbau erfahren und erstmals die Fähigkeit erkannt, dreidimensionale Schachfiguren aufzunehmen B. durch mechanische Klauen an einem Heimroboter, und führen Sie Mensch-Maschine-Funktionen aus, z. B. Schach spielen, jeder spielt Schach, Überprüfung der Notation usw.
 Claude ist auch faul geworden! Netizen: Lernen Sie, sich einen Urlaub zu gönnen
Sep 02, 2024 pm 01:56 PM
Claude ist auch faul geworden! Netizen: Lernen Sie, sich einen Urlaub zu gönnen
Sep 02, 2024 pm 01:56 PM
Der Schulstart steht vor der Tür und nicht nur die Schüler, die bald ins neue Semester starten, sollten auf sich selbst aufpassen, sondern auch die großen KI-Modelle. Vor einiger Zeit war Reddit voller Internetnutzer, die sich darüber beschwerten, dass Claude faul werde. „Sein Niveau ist stark gesunken, es kommt oft zu Pausen und sogar die Ausgabe wird sehr kurz. In der ersten Woche der Veröffentlichung konnte es ein komplettes 4-seitiges Dokument auf einmal übersetzen, aber jetzt kann es nicht einmal eine halbe Seite ausgeben.“ !
 Auf der Weltroboterkonferenz wurde dieser Haushaltsroboter, der „die Hoffnung auf eine zukünftige Altenpflege' in sich trägt, umzingelt
Aug 22, 2024 pm 10:35 PM
Auf der Weltroboterkonferenz wurde dieser Haushaltsroboter, der „die Hoffnung auf eine zukünftige Altenpflege' in sich trägt, umzingelt
Aug 22, 2024 pm 10:35 PM
Auf der World Robot Conference in Peking ist die Präsentation humanoider Roboter zum absoluten Mittelpunkt der Szene geworden. Am Stand von Stardust Intelligent führte der KI-Roboterassistent S1 drei große Darbietungen mit Hackbrett, Kampfkunst und Kalligraphie auf Ein Ausstellungsbereich, der sowohl Literatur als auch Kampfkunst umfasst, zog eine große Anzahl von Fachpublikum und Medien an. Durch das elegante Spiel auf den elastischen Saiten demonstriert der S1 eine feine Bedienung und absolute Kontrolle mit Geschwindigkeit, Kraft und Präzision. CCTV News führte einen Sonderbericht über das Nachahmungslernen und die intelligente Steuerung hinter „Kalligraphie“ durch. Firmengründer Lai Jie erklärte, dass hinter den seidenweichen Bewegungen die Hardware-Seite die beste Kraftkontrolle und die menschenähnlichsten Körperindikatoren (Geschwindigkeit, Belastung) anstrebt. usw.), aber auf der KI-Seite werden die realen Bewegungsdaten von Menschen gesammelt, sodass der Roboter stärker werden kann, wenn er auf eine schwierige Situation stößt, und lernen kann, sich schnell weiterzuentwickeln. Und agil
 Bekanntgabe der ACL 2024 Awards: Eines der besten Papers zum Thema Oracle Deciphering von HuaTech, GloVe Time Test Award
Aug 15, 2024 pm 04:37 PM
Bekanntgabe der ACL 2024 Awards: Eines der besten Papers zum Thema Oracle Deciphering von HuaTech, GloVe Time Test Award
Aug 15, 2024 pm 04:37 PM
Bei dieser ACL-Konferenz haben die Teilnehmer viel gewonnen. Die sechstägige ACL2024 findet in Bangkok, Thailand, statt. ACL ist die führende internationale Konferenz im Bereich Computerlinguistik und Verarbeitung natürlicher Sprache. Sie wird von der International Association for Computational Linguistics organisiert und findet jährlich statt. ACL steht seit jeher an erster Stelle, wenn es um akademischen Einfluss im Bereich NLP geht, und ist außerdem eine von der CCF-A empfohlene Konferenz. Die diesjährige ACL-Konferenz ist die 62. und hat mehr als 400 innovative Arbeiten im Bereich NLP eingereicht. Gestern Nachmittag gab die Konferenz den besten Vortrag und weitere Auszeichnungen bekannt. Diesmal gibt es 7 Best Paper Awards (zwei davon unveröffentlicht), 1 Best Theme Paper Award und 35 Outstanding Paper Awards. Die Konferenz verlieh außerdem drei Resource Paper Awards (ResourceAward) und einen Social Impact Award (
 Hongmeng Smart Travel S9 und die umfassende Einführungskonferenz für neue Produkte wurden gemeinsam mit einer Reihe neuer Blockbuster-Produkte veröffentlicht
Aug 08, 2024 am 07:02 AM
Hongmeng Smart Travel S9 und die umfassende Einführungskonferenz für neue Produkte wurden gemeinsam mit einer Reihe neuer Blockbuster-Produkte veröffentlicht
Aug 08, 2024 am 07:02 AM
Heute Nachmittag begrüßte Hongmeng Zhixing offiziell neue Marken und neue Autos. Am 6. August veranstaltete Huawei die Hongmeng Smart Xingxing S9 und die Huawei-Konferenz zur Einführung neuer Produkte mit umfassendem Szenario und brachte die Panorama-Smart-Flaggschiff-Limousine Xiangjie S9, das neue M7Pro und Huawei novaFlip, MatePad Pro 12,2 Zoll, das neue MatePad Air und Huawei Bisheng mit Mit vielen neuen Smart-Produkten für alle Szenarien, darunter die Laserdrucker der X1-Serie, FreeBuds6i, WATCHFIT3 und der Smart Screen S5Pro, von Smart Travel über Smart Office bis hin zu Smart Wear baut Huawei weiterhin ein Smart-Ökosystem für alle Szenarien auf, um Verbrauchern ein Smart-Erlebnis zu bieten Internet von allem. Hongmeng Zhixing: Huawei arbeitet mit chinesischen Partnern aus der Automobilindustrie zusammen, um die Modernisierung der Smart-Car-Industrie voranzutreiben
 Das Team von Li Feifei schlug ReKep vor, um Robotern räumliche Intelligenz zu verleihen und GPT-4o zu integrieren
Sep 03, 2024 pm 05:18 PM
Das Team von Li Feifei schlug ReKep vor, um Robotern räumliche Intelligenz zu verleihen und GPT-4o zu integrieren
Sep 03, 2024 pm 05:18 PM
Tiefe Integration von Vision und Roboterlernen. Wenn zwei Roboterhände reibungslos zusammenarbeiten, um Kleidung zu falten, Tee einzuschenken und Schuhe zu packen, gepaart mit dem humanoiden 1X-Roboter NEO, der in letzter Zeit für Schlagzeilen gesorgt hat, haben Sie vielleicht das Gefühl: Wir scheinen in das Zeitalter der Roboter einzutreten. Tatsächlich sind diese seidigen Bewegungen das Produkt fortschrittlicher Robotertechnologie + exquisitem Rahmendesign + multimodaler großer Modelle. Wir wissen, dass nützliche Roboter oft komplexe und exquisite Interaktionen mit der Umgebung erfordern und die Umgebung als Einschränkungen im räumlichen und zeitlichen Bereich dargestellt werden kann. Wenn Sie beispielsweise möchten, dass ein Roboter Tee einschenkt, muss der Roboter zunächst den Griff der Teekanne ergreifen und sie aufrecht halten, ohne den Tee zu verschütten, und ihn dann sanft bewegen, bis die Öffnung der Kanne mit der Öffnung der Tasse übereinstimmt , und neigen Sie dann die Teekanne in einem bestimmten Winkel. Das
 Getestet 7 Artefakte zur Videogenerierung auf „Sora-Ebene'. Wer hat die Fähigkeit, den „Eisernen Thron' zu besteigen?
Aug 05, 2024 pm 07:19 PM
Getestet 7 Artefakte zur Videogenerierung auf „Sora-Ebene'. Wer hat die Fähigkeit, den „Eisernen Thron' zu besteigen?
Aug 05, 2024 pm 07:19 PM
Herausgeber des Machine Power Report: Yang Wen Wer kann der King of AI-Videokreis werden? In der amerikanischen Fernsehserie „Game of Thrones“ gibt es einen „Eisernen Thron“. Der Legende nach wurde es vom riesigen Drachen „Schwarzer Tod“ erschaffen, der Tausende von von Feinden weggeworfenen Schwertern zum Schmelzen brachte und so höchste Autorität symbolisierte. Um auf diesem eisernen Stuhl zu sitzen, begannen die großen Familien zu kämpfen und zu kämpfen. Seit der Entstehung von Sora wurde im KI-Videokreis ein energisches „Game of Thrones“ gestartet. Zu den Hauptakteuren in diesem Spiel zählen RunwayGen-3 und Luma von der anderen Seite des Ozeans sowie die einheimischen Kuaishou Keling, ByteDream, und Zhimo. Spectrum Qingying, Vidu, PixVerseV2 usw. Heute werden wir bewerten und sehen, wer qualifiziert ist, auf dem „Eisernen Thron“ des KI-Videokreises zu sitzen. -1- Vincent Video



