 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Google Mathematical AI veröffentlicht einen Artikel in Nature: Proving beyond Wu Wenjun's 1978 theorem, demonstriert ein geometrisches Niveau von Weltklasse
Google Mathematical AI veröffentlicht einen Artikel in Nature: Proving beyond Wu Wenjun's 1978 theorem, demonstriert ein geometrisches Niveau von Weltklasse
Google Mathematical AI veröffentlicht einen Artikel in Nature: Proving beyond Wu Wenjun's 1978 theorem, demonstriert ein geometrisches Niveau von Weltklasse
Google DeepMind veröffentlicht die Natur erneut, die KI der Alpha-Serie kehrt zurück und das Mathematikniveau verbessert sich sprunghaft.
AlphaGeometry, keine menschliche Demonstration erforderlich, um das Geometrieniveau der IMO-Goldmedaillenspieler zu erreichen.

Es fühlt sich an, als hätte AlphaZero damals das Spiel „Das Go-Spiel ohne menschliches Wissen meistern“ gelernt.
AlphaGeometry hat 25 der meiner Meinung nach 30 geometrischen Theorem-Fragen mit Schwierigkeitsgrad richtig beantwortet, während der durchschnittliche menschliche Goldmedaillengewinner 25,9 richtig beantwortet hat. Darüber hinaus konnte die frühere SOTA-Methode (Wu Wenjun-Methode im Jahr 1978) nur 10 richtige Ergebnisse erzielen.
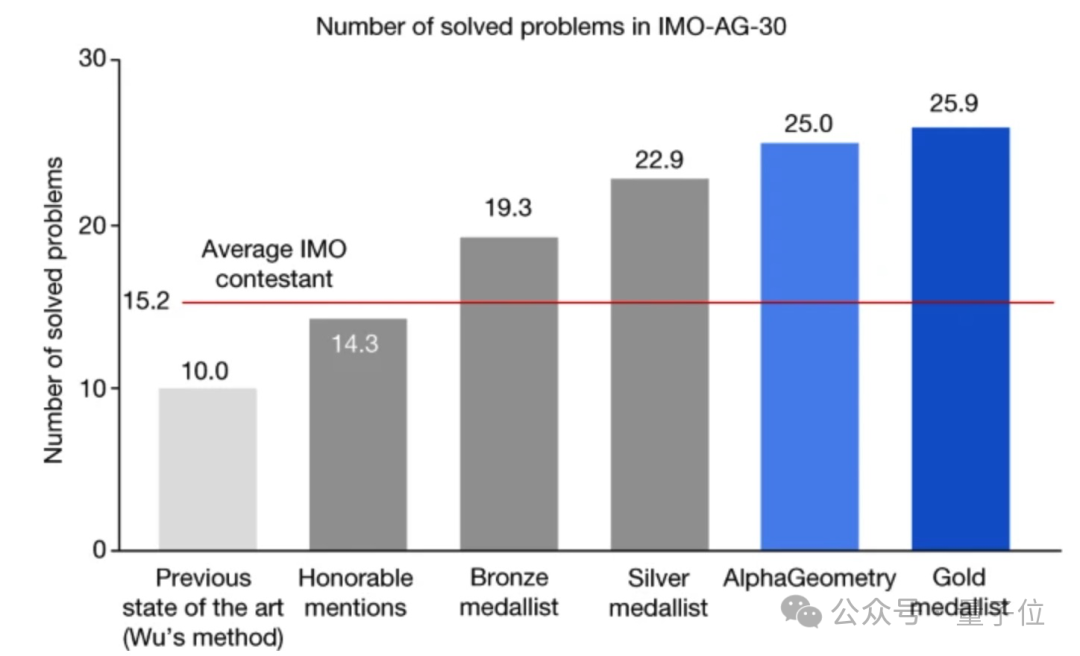
IMO-Goldmedaillengewinner Evan Chen(Evan Chen) war für die Auswertung der von der KI generierten Antworten verantwortlich:
Die Ausgabe von AlphaGeometry ist beeindruckend, sowohl zuverlässig als auch sauber. Frühere KI-Lösungen waren ein Zufall, was zu Ergebnissen führte, die manchmal eine manuelle Überprüfung erforderten.
Die Lösungen von AlphaGeometry haben eine überprüfbare Struktur, die sowohl von Maschinen überprüft als auch von Menschen verstanden werden kann. Es verwendet klassische Geometrieregeln wie Winkel und ähnliche Dreiecke, genau wie die Schüler.
Zusätzlich zu den herausragenden Ergebnissen gibt es in dieser Studie drei wichtige Punkte, die die Aufmerksamkeit der Branche auf sich gezogen haben:
- Es ist keine menschliche Demonstration erforderlich, das heißt, es wird nur KI-Training mit synthetischen Daten verwendet , Fortsetzung der selbstlernenden Go-Methode von AlphaZero.
- Großes Modell kombiniert mit anderen KI-Methoden, ähnlich den Gerüchten über AlphaGo und OpenAI Q*.
- Im Gegensatz zu vielen früheren Methoden kann AlphaGeometry für Menschen lesbare Beweisprozesse generieren, und sowohl das Modell als auch der Code sind Open Source.
Das Team ist davon überzeugt, dass AlphaGeometry einen potenziellen Rahmen für die Erlangung fortgeschrittener Denkfähigkeiten und die Entdeckung neuen Wissens bietet.
Dies kann dazu beitragen, den Theorembeweis in der künstlichen Intelligenz voranzutreiben – was als wichtiger Schritt beim Aufbau von AGI angesehen wird.

Außerdem erkundigte sich Qubits während des Kommunikationsprozesses mit dem Team des Autors, ob AlphaGeometry wirklich an einem IMO-Wettbewerb teilnehmen dürfe, so wie AlphaGo den menschlichen Go-Champion herausgefordert hätte.
Sie sagten, dass sie hart daran arbeiten, die Fähigkeiten des Systems zu verbessern, und dass sie die KI auch in die Lage versetzen müssen, ein breiteres Spektrum mathematischer Probleme über die Geometrie hinaus zu lösen.
KI beweist, dass Geometrie auch Hilfslinien zeichnet
Früher konnte das KI-System geometrische Probleme nicht gut lösen und blieb aufgrund des Mangels an hochwertigen Trainingsdaten stecken.
Menschen, die Geometrie lernen, können vorhandenes Wissen über Bilder nutzen, um mithilfe von Papier und Stift neue und komplexere geometrische Eigenschaften und Beziehungen zu entdecken.
Zu diesem Zweck hat das Google-Team 1 Milliarde zufällige geometrische Objektdiagramme sowie alle Beziehungen zwischen ihren Punkten und Linien generiert und schließlich 100 Millionen einzigartige Theoreme und Beweise verschiedener Schwierigkeitsgrade herausgesucht. AlphaGeometry wurde komplett von Grund auf trainiert diese Daten.

Das System besteht aus zwei Modulen, die zusammenarbeiten, um komplexe geometrische Beweise zu finden.
- Sprachmodell, das die Geometrie vorhersagt, die zur Lösung des Problems verwendet werden kann (d. h. Hinzufügen von Hilfslinien) .
- Symbolische Argumentationsmaschine, die logische Regeln verwendet, um Schlussfolgerungen abzuleiten.
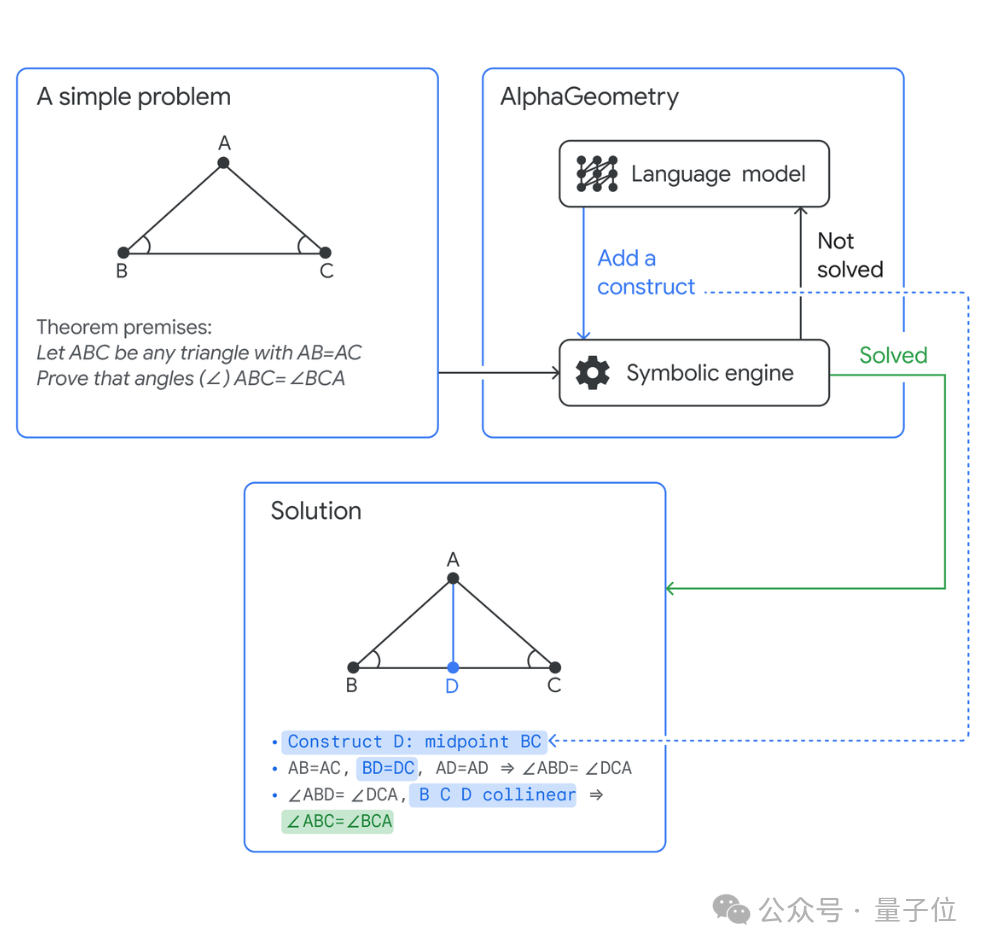
Der Erstautor Trieu Trinh stellte vor, dass der Betriebsprozess von AlphaGeometry der Art und Weise ähnelt, wie das menschliche Gehirn in zwei Typen unterteilt wird: schnell und langsam.
Dies ist das Konzept von „System 1, System 2“, das im Bestseller „Thinking Fast and Slow“ des Nobelpreisträgers Daniel Kahneman populär gemacht wurde.
System 1 liefert schnelle, intuitive Ideen, während System 2 durchdachtere und rationalere Entscheidungen ermöglicht.
Einerseits sind Sprachmodelle gut darin, Muster und Beziehungen in Daten zu erkennen und potenziell nützliche Hilfsstrukturen schnell vorherzusagen, ihnen fehlt jedoch oft die Fähigkeit, ihre Entscheidungen schlüssig zu begründen oder zu erklären.
Andererseits basieren symbolische Argumentationsmaschinen auf formaler Logik und verwenden explizite Regeln, um Schlussfolgerungen zu ziehen. Sie sind rational und erklärbar, aber sie sind langsam und unflexibel, insbesondere wenn sie sich allein mit großen, komplexen Problemen befassen.
Beim Lösen einer IMO 2015-Wettbewerbsfrage ist der blaue Teil die vom Sprachmodell von AlphaGeometry hinzugefügte Hilfsstruktur und der grüne Teil die optimierte Version des endgültigen Beweises mit insgesamt 109 Schritten.
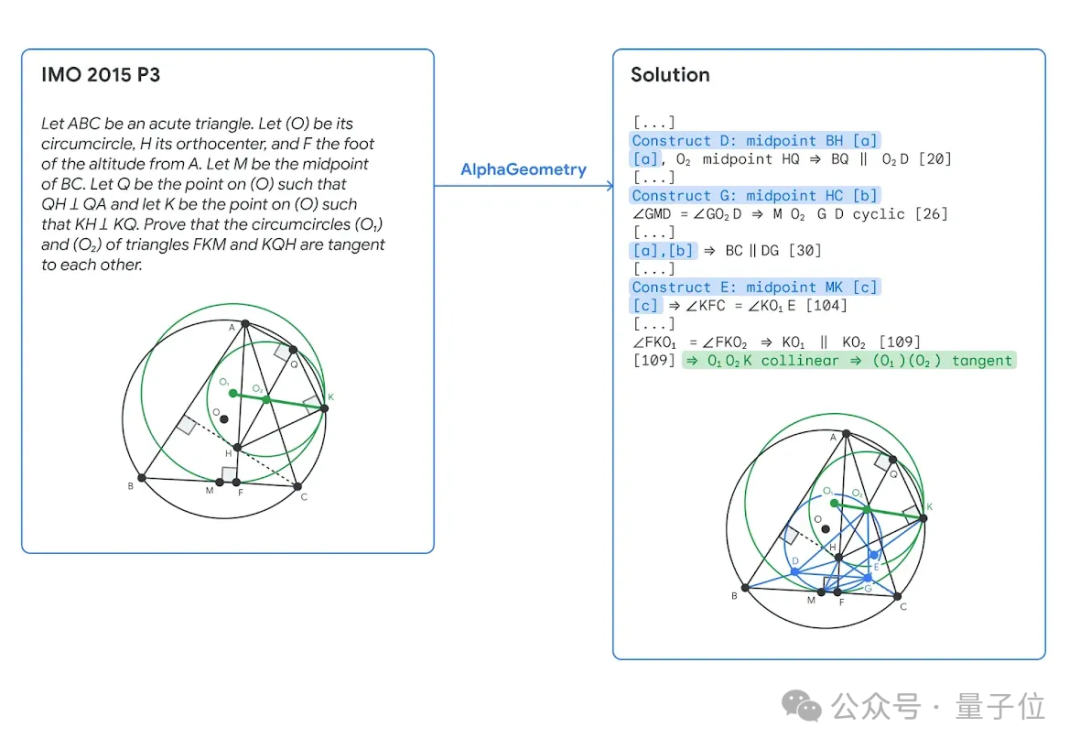
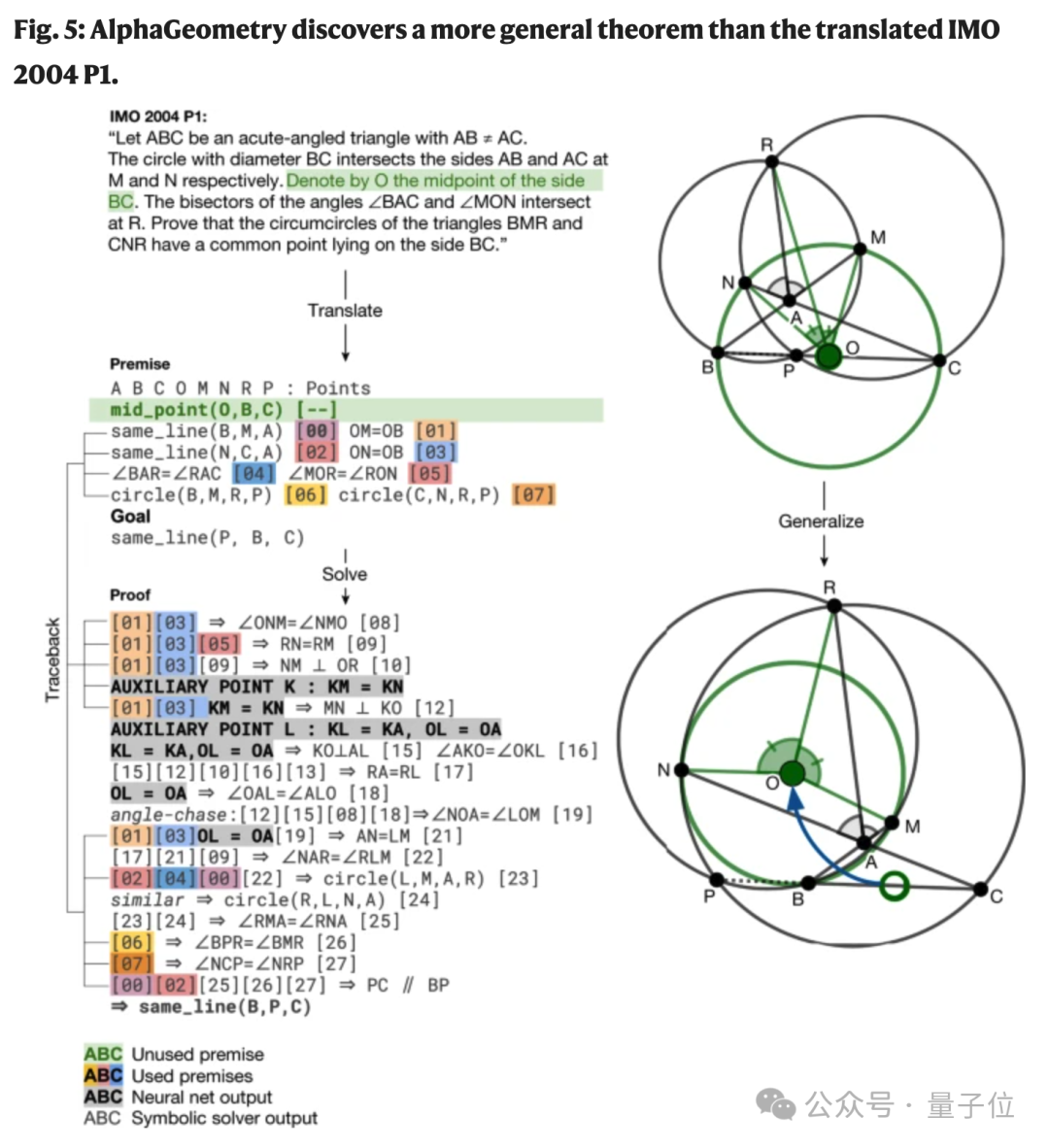
Während des Lösungsprozesses des Problems entdeckte AlphaGeometry auch eine ungenutzte Voraussetzung im IMO-Wettbewerbsproblem von 2004 und entdeckte damit eine breitere Version des Theorems.
Es kann bewiesen werden, dass P, B und C kollinear sind, ohne die Bedingung, dass O der Mittelpunkt von BC ist.
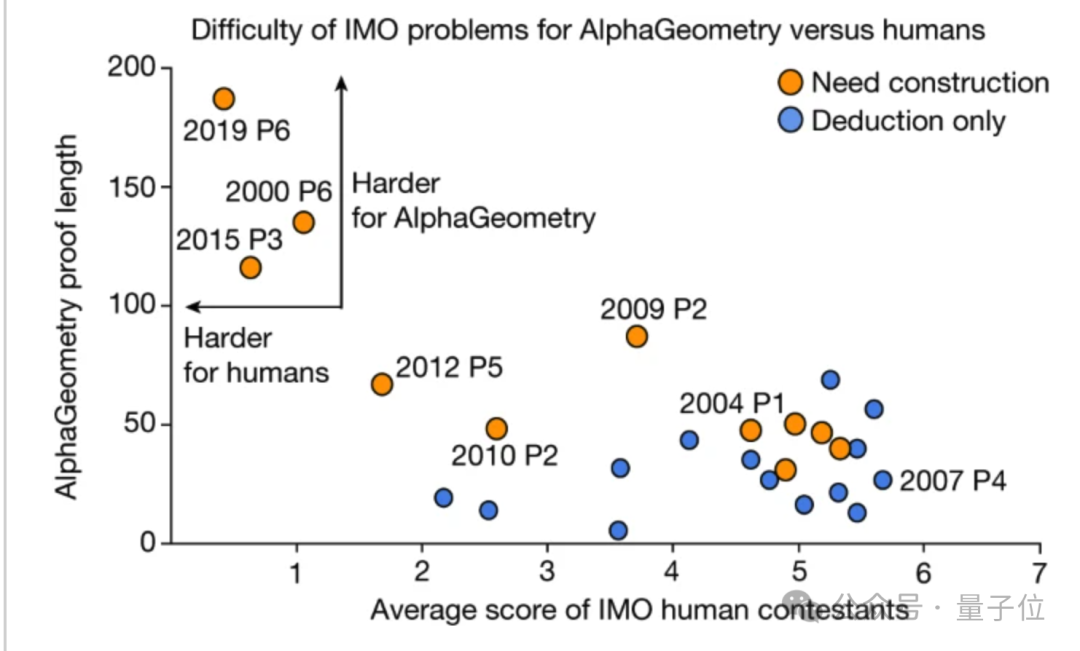
Darüber hinaus haben Untersuchungen ergeben, dass AlphaGeometry für die drei Probleme mit den niedrigsten menschlichen Werten auch einen sehr langen Prüfprozess und die Hinzufügung vieler zu lösender Hilfsstrukturen erfordert.
Aber bei den relativ einfachen Fragen gab es keine signifikante Korrelation zwischen der durchschnittlichen menschlichen Punktzahl und der Länge der von der KI generierten Beweise (p = −0,06).
Noch eine Sache
Bezüglich der Verbindung und des Unterschieds zwischen AlphaGeometry und AlphaGo stellte der Google-Wissenschaftler Quoc Le während des Kommunikationsprozesses mit dem Team vor:
Sie befinden sich beide in einer sehr komplexen Entscheidung- Platz suchen, aber die Methode von AlphaGo ist traditioneller (Hinweis: Das neuronale Netzwerk ist für die Mustererkennung verantwortlich) Das neuronale Netzwerk in AlphaGeometry ist dafür verantwortlich, die nächste zu ergreifende Aktion vorzuschlagen und den Suchalgorithmus in die richtige Richtung zu lenken im Entscheidungsraum.
Obwohl dieses Ergebnis nach der Alpha-Serie benannt ist und die erste Einheit auch Google DeepMind ist, ist der Autor tatsächlich ein ehemaliges Google Brain-Mitglied.
Meister Quoc Le braucht keine Vorstellung. Der erste Autor Trieu Trinh und der korrespondierende Autor Thang Luong haben beide sechs oder sieben Jahre lang bei Google gearbeitet. Thang Luong selbst war meiner Meinung nach auch ein IMO-Spieler.
Unter den beiden chinesischen Autoren ist He He Assistenzprofessor an der New York University. Wu Yuhuai war zuvor an der Erforschung des großen mathematischen Modells Minerva von Google beteiligt und hat nun Google verlassen, um sich Musks Team anzuschließen und einer der Mitbegründer von xAI zu werden.
Papieradresse: https://www.nature.com/articles/s41586-023-06747-5.
Referenzlink:
[1]https://www.nature.com/articles/d4186-024-00141-5.
[2]https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry.
Das obige ist der detaillierte Inhalt vonGoogle Mathematical AI veröffentlicht einen Artikel in Nature: Proving beyond Wu Wenjun's 1978 theorem, demonstriert ein geometrisches Niveau von Weltklasse. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1393
1393
 52
52
 1209
1209
 24
24
 Sesame Open Door Exchange -Webseite Registrierung Link Gate Trading App Registrierung Website Neueste
Feb 28, 2025 am 11:06 AM
Sesame Open Door Exchange -Webseite Registrierung Link Gate Trading App Registrierung Website Neueste
Feb 28, 2025 am 11:06 AM
In diesem Artikel wird der Registrierungsprozess der Webversion Sesam Open Exchange (GATE.IO) und die Gate Trading App im Detail vorgestellt. Unabhängig davon, ob es sich um eine Webregistrierung oder eine App -Registrierung handelt, müssen Sie die offizielle Website oder den offiziellen App Store besuchen, um die Genuine App herunterzuladen, und dann den Benutzernamen, das Kennwort, die E -Mail, die Mobiltelefonnummer und die anderen Informationen eingeben und eine E -Mail- oder Mobiltelefonüberprüfung abschließen.
 Warum kann der Bybit -Exchange -Link nicht direkt heruntergeladen und installiert werden?
Feb 21, 2025 pm 10:57 PM
Warum kann der Bybit -Exchange -Link nicht direkt heruntergeladen und installiert werden?
Feb 21, 2025 pm 10:57 PM
Warum kann der Bybit -Exchange -Link nicht direkt heruntergeladen und installiert werden? Bitbit ist eine Kryptowährungsbörse, die den Benutzern Handelsdienste anbietet. Die mobilen Apps der Exchange können aus den folgenden Gründen nicht direkt über AppStore oder Googleplay heruntergeladen werden: 1. App Store -Richtlinie beschränkt Apple und Google daran, strenge Anforderungen an die im App Store zulässigen Anwendungsarten zu haben. Kryptowährungsanträge erfüllen diese Anforderungen häufig nicht, da sie Finanzdienstleistungen einbeziehen und spezifische Vorschriften und Sicherheitsstandards erfordern. 2. Die Einhaltung von Gesetzen und Vorschriften In vielen Ländern werden Aktivitäten im Zusammenhang mit Kryptowährungstransaktionen reguliert oder eingeschränkt. Um diese Vorschriften einzuhalten, kann die Bitbit -Anwendung nur über offizielle Websites oder andere autorisierte Kanäle verwendet werden
 Sesam Open Door Exchange Webseite Login Neueste Version Gateio Offizieller Website Eingang
Mar 04, 2025 pm 11:48 PM
Sesam Open Door Exchange Webseite Login Neueste Version Gateio Offizieller Website Eingang
Mar 04, 2025 pm 11:48 PM
Eine detaillierte Einführung in den Anmeldungsbetrieb der Sesame Open Exchange -Webversion, einschließlich Anmeldeschritte und Kennwortwiederherstellungsprozess.
 Sesame Open Door Trading Platform Download Mobile Version Gateio Trading Platform Download -Adresse
Feb 28, 2025 am 10:51 AM
Sesame Open Door Trading Platform Download Mobile Version Gateio Trading Platform Download -Adresse
Feb 28, 2025 am 10:51 AM
Es ist wichtig, einen formalen Kanal auszuwählen, um die App herunterzuladen und die Sicherheit Ihres Kontos zu gewährleisten.
 Top 10 für Crypto Digital Asset Trading App (2025 Global Ranking) empfohlen
Mar 18, 2025 pm 12:15 PM
Top 10 für Crypto Digital Asset Trading App (2025 Global Ranking) empfohlen
Mar 18, 2025 pm 12:15 PM
Dieser Artikel empfiehlt die Top Ten Ten Cryptocurrency -Handelsplattformen, die es wert sind, auf Binance, OKX, Gate.io, Bitflyer, Kucoin, Bybit, Coinbase Pro, Kraken, BYDFI und Xbit -dezentrale Börsen geachtet zu werden. Diese Plattformen haben ihre eigenen Vorteile in Bezug auf Transaktionswährungsmenge, Transaktionstyp, Sicherheit, Konformität und Besonderheiten. Die Auswahl einer geeigneten Plattform erfordert eine umfassende Überlegung, die auf eigener Handelserfahrung, Risikotoleranz und Investitionspräferenzen basiert. Ich hoffe, dieser Artikel hilft Ihnen dabei, den besten Anzug für sich selbst zu finden
 Binance Binance Offizielle Website Neueste Version Anmeldeportal
Feb 21, 2025 pm 05:42 PM
Binance Binance Offizielle Website Neueste Version Anmeldeportal
Feb 21, 2025 pm 05:42 PM
Befolgen Sie diese einfachen Schritte, um auf die neueste Version des Binance -Website -Login -Portals zuzugreifen. Gehen Sie zur offiziellen Website und klicken Sie in der oberen rechten Ecke auf die Schaltfläche "Anmeldung". Wählen Sie Ihre vorhandene Anmeldemethode. Geben Sie Ihre registrierte Handynummer oder E -Mail und Kennwort ein und vervollständigen Sie die Authentifizierung (z. B. Mobilfifizierungscode oder Google Authenticator). Nach einer erfolgreichen Überprüfung können Sie auf das neueste Version des offiziellen Website -Login -Portals von Binance zugreifen.
 Bitget Trading Platform Offizielle App -Download- und Installationsadresse
Feb 25, 2025 pm 02:42 PM
Bitget Trading Platform Offizielle App -Download- und Installationsadresse
Feb 25, 2025 pm 02:42 PM
Dieser Leitfaden enthält detaillierte Download- und Installationsschritte für die offizielle Bitget Exchange -App, die für Android- und iOS -Systeme geeignet ist. Der Leitfaden integriert Informationen aus mehreren maßgeblichen Quellen, einschließlich der offiziellen Website, dem App Store und Google Play, und betont Überlegungen während des Downloads und des Kontoverwaltung. Benutzer können die App aus offiziellen Kanälen herunterladen, einschließlich App Store, offizieller Website APK Download und offizieller Website -Sprung sowie vollständige Registrierung, Identitätsüberprüfung und Sicherheitseinstellungen. Darüber hinaus deckt der Handbuch häufig gestellte Fragen und Überlegungen ab, wie z.
 Die neueste Download -Adresse des Bitgets im Jahr 2025: Schritte zum Erhalten der offiziellen App
Feb 25, 2025 pm 02:54 PM
Die neueste Download -Adresse des Bitgets im Jahr 2025: Schritte zum Erhalten der offiziellen App
Feb 25, 2025 pm 02:54 PM
Dieser Leitfaden enthält detaillierte Download- und Installationsschritte für die offizielle Bitget Exchange -App, die für Android- und iOS -Systeme geeignet ist. Der Leitfaden integriert Informationen aus mehreren maßgeblichen Quellen, einschließlich der offiziellen Website, dem App Store und Google Play, und betont Überlegungen während des Downloads und des Kontoverwaltung. Benutzer können die App aus offiziellen Kanälen herunterladen, einschließlich App Store, offizieller Website APK Download und offizieller Website -Sprung sowie vollständige Registrierung, Identitätsüberprüfung und Sicherheitseinstellungen. Darüber hinaus deckt der Handbuch häufig gestellte Fragen und Überlegungen ab, wie z.



