Verwenden Sie Python, um den Löschoperationscode des B+-Baums zu schreiben

Für den Löschvorgang des B+-Baums muss zunächst der Standort des gelöschten Knotens ermittelt und dann die Anzahl der Schlüssel des Knotens ermittelt werden.

Wenn die Anzahl der Schlüssel im Knoten die Mindestanzahl überschreitet, löschen Sie ihn einfach direkt.

Löschen Sie „40“ wie unten gezeigt:

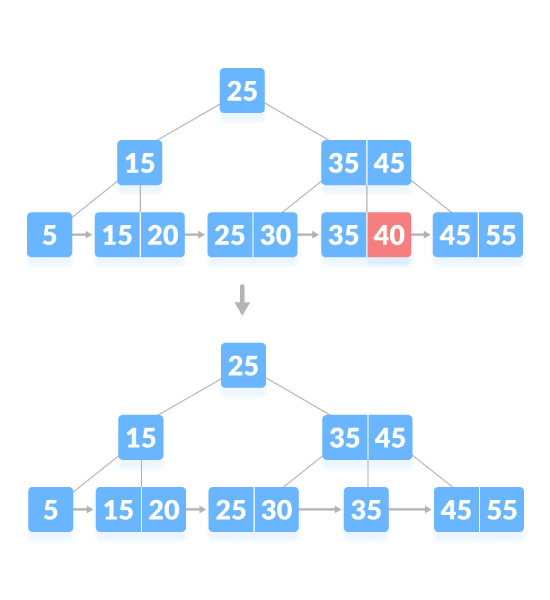
Wenn der Knoten eine genaue Mindestanzahl an Schlüsseln aufweist, erfordert das Löschen eine Entlehnung vom Geschwisterknoten und das Hinzufügen des Zwischenschlüssels des Geschwisterknotens zum übergeordneten Knoten. Löschen Sie wie unten gezeigt „5“:

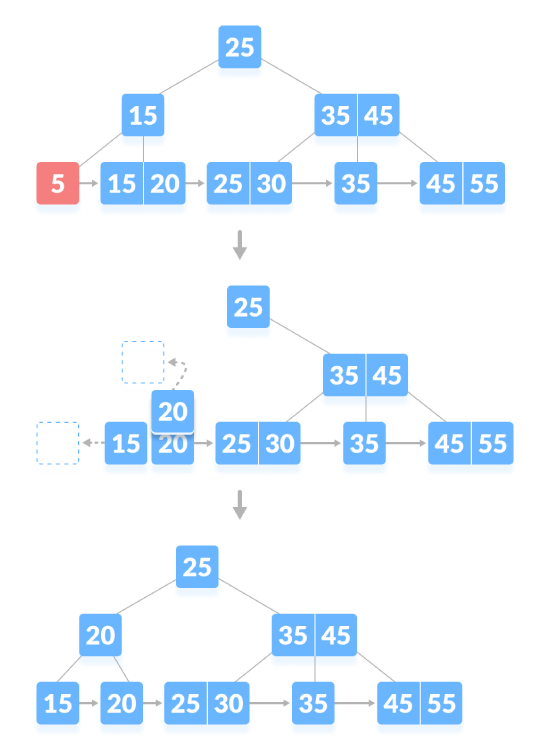
Löschen Sie den Inhaltsknoten. Wenn die Anzahl der Schlüssel im Knoten die Mindestanzahl überschreitet, löschen Sie einfach den Schlüssel vom Blattknoten und den Schlüssel vom internen Knoten . Füllen Sie leere Räume in internen Knoten mit Inorder-Nachfolgern. Löschen Sie wie unten gezeigt „45“:

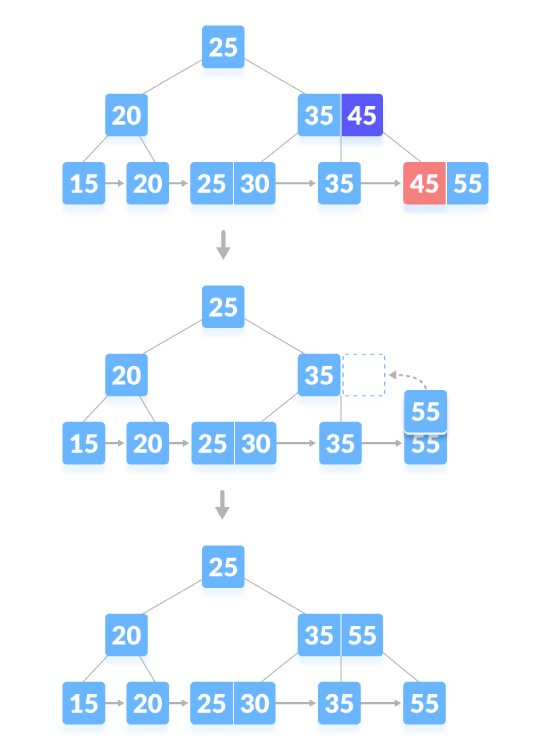
Löschen Sie den Inhaltsknoten. Wenn der Knoten eine genaue Mindestanzahl an Schlüsseln enthält, löschen Sie den Schlüssel, leihen Sie einen Schlüssel direkt vom Geschwisterknoten aus und füllen Sie ihn aus Index mit dem geliehenen Schlüssel des Leerraums. Löschen Sie wie unten gezeigt „35“:

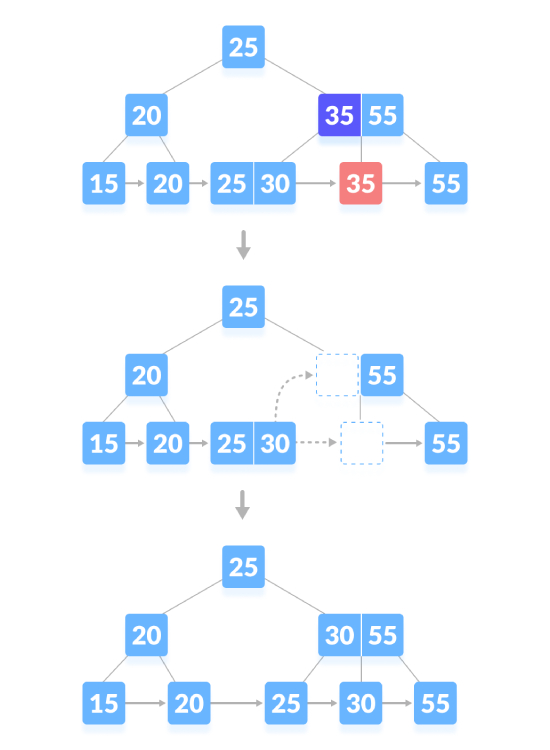
Löschen Sie den Inhaltsknoten und erstellen Sie ein Leerzeichen über dem übergeordneten Knoten. Nachdem Sie einen Schlüssel gelöscht haben, führen Sie den leeren Raum mit seinen Geschwistern zusammen und füllen Sie den leeren Raum im übergeordneten Knoten mit dem Inorder-Nachfolger. Wie unten gezeigt, löschen Sie „25“:

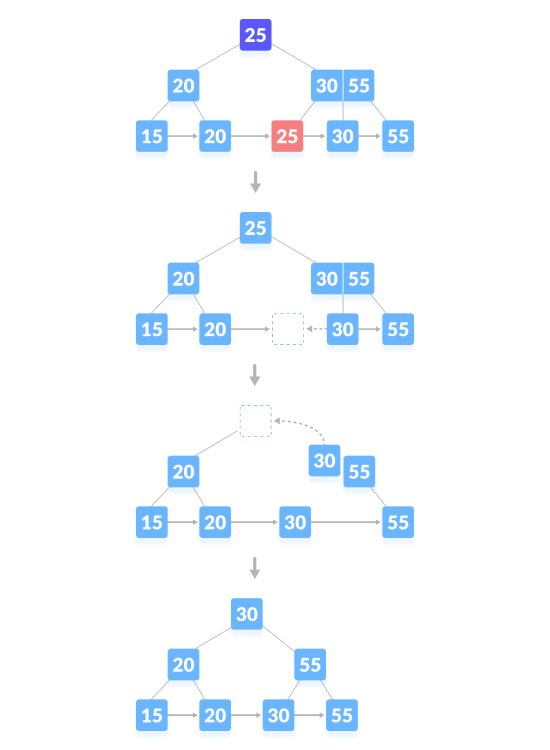
Der Löschvorgang, der zu einer Verkleinerung der Baumhöhe führt, wie unten gezeigt, löschen Sie „55“:

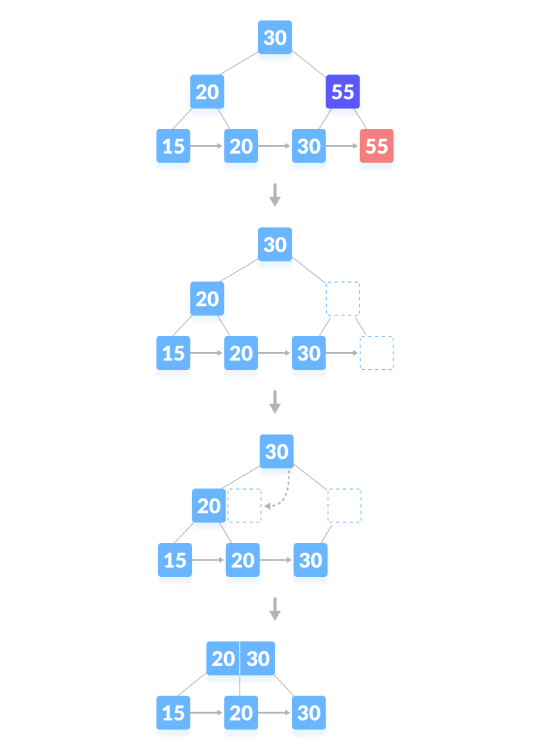
Python implementiert den B+-Baumlöschvorgang

import math
# 创建节点
class Node:
    def __init__(self, order):
        self.order = order
        self.values = []
        self.keys = []
        self.nextKey = None
        self.parent = None
        self.check_leaf = False

# 插入叶子
    def insert_at_leaf(self, leaf, value, key):
        if (self.values):
            temp1 = self.values
            for i in range(len(temp1)):
                if (value == temp1[i]):
                    self.keys[i].append(key)
                    break
                elif (value < temp1[i]):
                    self.values = self.values[:i] + [value] + self.values[i:]
                    self.keys = self.keys[:i] + [[key]] + self.keys[i:]
                    break
                elif (i + 1 == len(temp1)):
                    self.values.append(value)
                    self.keys.append([key])
                    break
        else:
            self.values = [value]
            self.keys = [[key]]


# B+树
class BplusTree:
    def __init__(self, order):
        self.root = Node(order)
        self.root.check_leaf = True

    # 插入节点
    def insert(self, value, key):
        value = str(value)
        old_node = self.search(value)
        old_node.insert_at_leaf(old_node, value, key)

        if (len(old_node.values) == old_node.order):
            node1 = Node(old_node.order)
            node1.check_leaf = True
            node1.parent = old_node.parent
            mid = int(math.ceil(old_node.order / 2)) - 1
            node1.values = old_node.values[mid + 1:]
            node1.keys = old_node.keys[mid + 1:]
            node1.nextKey = old_node.nextKey
            old_node.values = old_node.values[:mid + 1]
            old_node.keys = old_node.keys[:mid + 1]
            old_node.nextKey = node1
            self.insert_in_parent(old_node, node1.values[0], node1)

    def search(self, value):
        current_node = self.root
        while(current_node.check_leaf == False):
            temp2 = current_node.values
            for i in range(len(temp2)):
                if (value == temp2[i]):
                    current_node = current_node.keys[i + 1]
                    break
                elif (value < temp2[i]):
                    current_node = current_node.keys[i]
                    break
                elif (i + 1 == len(current_node.values)):
                    current_node = current_node.keys[i + 1]
                    break
        return current_node

    # 查找节点
    def find(self, value, key):
        l = self.search(value)
        for i, item in enumerate(l.values):
            if item == value:
                if key in l.keys[i]:
                    return True
                else:
                    return False
        return False

    # 在父级插入
    def insert_in_parent(self, n, value, ndash):
        if (self.root == n):
            rootNode = Node(n.order)
            rootNode.values = [value]
            rootNode.keys = [n, ndash]
            self.root = rootNode
            n.parent = rootNode
            ndash.parent = rootNode
            return

        parentNode = n.parent
        temp3 = parentNode.keys
        for i in range(len(temp3)):
            if (temp3[i] == n):
                parentNode.values = parentNode.values[:i] + \
                    [value] + parentNode.values[i:]
                parentNode.keys = parentNode.keys[:i +
                                                  1] + [ndash] + parentNode.keys[i + 1:]
                if (len(parentNode.keys) > parentNode.order):
                    parentdash = Node(parentNode.order)
                    parentdash.parent = parentNode.parent
                    mid = int(math.ceil(parentNode.order / 2)) - 1
                    parentdash.values = parentNode.values[mid + 1:]
                    parentdash.keys = parentNode.keys[mid + 1:]
                    value_ = parentNode.values[mid]
                    if (mid == 0):
                        parentNode.values = parentNode.values[:mid + 1]
                    else:
                        parentNode.values = parentNode.values[:mid]
                    parentNode.keys = parentNode.keys[:mid + 1]
                    for j in parentNode.keys:
                        j.parent = parentNode
                    for j in parentdash.keys:
                        j.parent = parentdash
                    self.insert_in_parent(parentNode, value_, parentdash)

    # 删除节点
    def delete(self, value, key):
        node_ = self.search(value)

        temp = 0
        for i, item in enumerate(node_.values):
            if item == value:
                temp = 1

                if key in node_.keys[i]:
                    if len(node_.keys[i]) > 1:
                        node_.keys[i].pop(node_.keys[i].index(key))
                    elif node_ == self.root:
                        node_.values.pop(i)
                        node_.keys.pop(i)
                    else:
                        node_.keys[i].pop(node_.keys[i].index(key))
                        del node_.keys[i]
                        node_.values.pop(node_.values.index(value))
                        self.deleteEntry(node_, value, key)
                else:
                    print("Value not in Key")
                    return
        if temp == 0:
            print("Value not in Tree")
            return

    # 删除条目
    def deleteEntry(self, node_, value, key):

        if not node_.check_leaf:
            for i, item in enumerate(node_.keys):
                if item == key:
                    node_.keys.pop(i)
                    break
            for i, item in enumerate(node_.values):
                if item == value:
                    node_.values.pop(i)
                    break

        if self.root == node_ and len(node_.keys) == 1:
            self.root = node_.keys[0]
            node_.keys[0].parent = None
            del node_
            return
        elif (len(node_.keys) < int(math.ceil(node_.order / 2)) and node_.check_leaf == False) or (len(node_.values) < int(math.ceil((node_.order - 1) / 2)) and node_.check_leaf == True):

            is_predecessor = 0
            parentNode = node_.parent
            PrevNode = -1
            NextNode = -1
            PrevK = -1
            PostK = -1
            for i, item in enumerate(parentNode.keys):

                if item == node_:
                    if i > 0:
                        PrevNode = parentNode.keys[i - 1]
                        PrevK = parentNode.values[i - 1]

                    if i < len(parentNode.keys) - 1:
                        NextNode = parentNode.keys[i + 1]
                        PostK = parentNode.values[i]

            if PrevNode == -1:
                ndash = NextNode
                value_ = PostK
            elif NextNode == -1:
                is_predecessor = 1
                ndash = PrevNode
                value_ = PrevK
            else:
                if len(node_.values) + len(NextNode.values) < node_.order:
                    ndash = NextNode
                    value_ = PostK
                else:
                    is_predecessor = 1
                    ndash = PrevNode
                    value_ = PrevK

            if len(node_.values) + len(ndash.values) < node_.order:
                if is_predecessor == 0:
                    node_, ndash = ndash, node_
                ndash.keys += node_.keys
                if not node_.check_leaf:
                    ndash.values.append(value_)
                else:
                    ndash.nextKey = node_.nextKey
                ndash.values += node_.values

                if not ndash.check_leaf:
                    for j in ndash.keys:
                        j.parent = ndash

                self.deleteEntry(node_.parent, value_, node_)
                del node_
            else:
                if is_predecessor == 1:
                    if not node_.check_leaf:
                        ndashpm = ndash.keys.pop(-1)
                        ndashkm_1 = ndash.values.pop(-1)
                        node_.keys = [ndashpm] + node_.keys
                        node_.values = [value_] + node_.values
                        parentNode = node_.parent
                        for i, item in enumerate(parentNode.values):
                            if item == value_:
                                p.values[i] = ndashkm_1
                                break
                    else:
                        ndashpm = ndash.keys.pop(-1)
                        ndashkm = ndash.values.pop(-1)
                        node_.keys = [ndashpm] + node_.keys
                        node_.values = [ndashkm] + node_.values
                        parentNode = node_.parent
                        for i, item in enumerate(p.values):
                            if item == value_:
                                parentNode.values[i] = ndashkm
                                break
                else:
                    if not node_.check_leaf:
                        ndashp0 = ndash.keys.pop(0)
                        ndashk0 = ndash.values.pop(0)
                        node_.keys = node_.keys + [ndashp0]
                        node_.values = node_.values + [value_]
                        parentNode = node_.parent
                        for i, item in enumerate(parentNode.values):
                            if item == value_:
                                parentNode.values[i] = ndashk0
                                break
                    else:
                        ndashp0 = ndash.keys.pop(0)
                        ndashk0 = ndash.values.pop(0)
                        node_.keys = node_.keys + [ndashp0]
                        node_.values = node_.values + [ndashk0]
                        parentNode = node_.parent
                        for i, item in enumerate(parentNode.values):
                            if item == value_:
                                parentNode.values[i] = ndash.values[0]
                                break

                if not ndash.check_leaf:
                    for j in ndash.keys:
                        j.parent = ndash
                if not node_.check_leaf:
                    for j in node_.keys:
                        j.parent = node_
                if not parentNode.check_leaf:
                    for j in parentNode.keys:
                        j.parent = parentNode


# 输出B+树
def printTree(tree):
    lst = [tree.root]
    level = [0]
    leaf = None
    flag = 0
    lev_leaf = 0

    node1 = Node(str(level[0]) + str(tree.root.values))

    while (len(lst) != 0):
        x = lst.pop(0)
        lev = level.pop(0)
        if (x.check_leaf == False):
            for i, item in enumerate(x.keys):
                print(item.values)
        else:
            for i, item in enumerate(x.keys):
                print(item.values)
            if (flag == 0):
                lev_leaf = lev
                leaf = x
                flag = 1

record_len = 3
bplustree = BplusTree(record_len)
bplustree.insert(&#x27;5&#x27;, &#x27;33&#x27;)
bplustree.insert(&#x27;15&#x27;, &#x27;21&#x27;)
bplustree.insert(&#x27;25&#x27;, &#x27;31&#x27;)
bplustree.insert(&#x27;35&#x27;, &#x27;41&#x27;)
bplustree.insert(&#x27;45&#x27;, &#x27;10&#x27;)

printTree(bplustree)

if(bplustree.find(&#x27;5&#x27;, &#x27;34&#x27;)):
    print("Found")
else:
    print("Not found")

Das obige ist der detaillierte Inhalt vonVerwenden Sie Python, um den Löschoperationscode des B+-Baums zu schreiben. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!