 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Theorie und Techniken der Gewichtsaktualisierung in neuronalen Netzen
Theorie und Techniken der Gewichtsaktualisierung in neuronalen Netzen
Theorie und Techniken der Gewichtsaktualisierung in neuronalen Netzen

Die Gewichtsaktualisierung im neuronalen Netzwerk besteht darin, die Verbindungsgewichte zwischen Neuronen im Netzwerk mithilfe von Methoden wie dem Backpropagation-Algorithmus anzupassen, um die Leistung des Netzwerks zu verbessern. In diesem Artikel werden das Konzept und die Methode der Gewichtsaktualisierung vorgestellt, um den Lesern ein besseres Verständnis des Trainingsprozesses neuronaler Netze zu ermöglichen.
1. Konzept
Die Gewichte in neuronalen Netzen sind Parameter, die verschiedene Neuronen verbinden und die Stärke der Signalübertragung bestimmen. Jedes Neuron empfängt das Signal von der vorherigen Schicht, multipliziert es mit dem Gewicht der Verbindung, fügt einen Bias-Term hinzu und wird schließlich durch die Aktivierungsfunktion aktiviert und an die nächste Schicht weitergeleitet. Daher wirkt sich die Größe des Gewichts direkt auf die Stärke und Richtung des Signals aus, was wiederum Auswirkungen auf die Ausgabe des neuronalen Netzwerks hat.
Der Zweck der Gewichtsaktualisierung besteht darin, die Leistung des neuronalen Netzwerks zu optimieren. Während des Trainingsprozesses passt sich das neuronale Netzwerk an die Trainingsdaten an, indem es die Gewichte zwischen den Neuronen kontinuierlich anpasst, um die Vorhersagefähigkeit der Testdaten zu verbessern. Durch die Anpassung der Gewichte kann das neuronale Netzwerk die Trainingsdaten besser anpassen und dadurch die Vorhersagegenauigkeit verbessern. Auf diese Weise kann das neuronale Netzwerk die Ergebnisse unbekannter Daten genauer vorhersagen und eine bessere Leistung erzielen.
2. Methode
Zu den häufig verwendeten Methoden zur Gewichtsaktualisierung in neuronalen Netzen gehören Gradientenabstieg, stochastischer Gradientenabstieg und Batch-Gradientenabstieg.
Gradientenabstiegsmethode
Die Gradientenabstiegsmethode ist eine der grundlegendsten Methoden zur Gewichtsaktualisierung. Ihre Grundidee besteht darin, das Gewicht durch Berechnung des Gradienten der Verlustfunktion zum Gewicht (d. h. der Ableitung von) zu aktualisieren die Verlustfunktion zum Gewicht), um die Verlustfunktion zu minimieren. Konkret sind die Schritte der Gradientenabstiegsmethode wie folgt:
Zuerst müssen wir eine Verlustfunktion definieren, um die Leistung des neuronalen Netzwerks anhand der Trainingsdaten zu messen. Normalerweise wählen wir den mittleren quadratischen Fehler (MSE) als Verlustfunktion, der wie folgt definiert ist:
MSE=frac{1}{n}sum_{i=1}^{n}(y_i-hat {y_i })^2
wobei y_i den wahren Wert der i-ten Stichprobe darstellt, hat{y_i} den vom neuronalen Netzwerk vorhergesagten Wert der i-ten Stichprobe darstellt und n die Gesamtzahl darstellt Proben.
Dann müssen wir die Ableitung der Verlustfunktion nach dem Gewicht, also dem Gradienten, berechnen. Insbesondere kann für jedes Gewicht w_{ij} im neuronalen Netzwerk sein Gradient mit der folgenden Formel berechnet werden:
frac{partial MSE}{partial w_{ij}}=frac{2}{n}sum_ { k=1}^{n}(y_k-hat{y_k})cdot f'(sum_{j=1}^{m}w_{ij}x_{kj})cdot x_{ki}
wo , n stellt die Gesamtzahl der Stichproben dar, m stellt die Eingabeschichtgröße des neuronalen Netzwerks dar, x_{kj} stellt das j-te Eingabemerkmal der k-ten Stichprobe dar, f(cdot) stellt die Aktivierungsfunktion dar und f'( cdot) stellt die Ableitung der Aktivierungsfunktion dar.
Schließlich können wir die Gewichte durch die folgende Formel aktualisieren:
w_{ij}=w_{ij}-alphacdotfrac{partial MSE}{partial w_{ij}}
wobei Alpha Lernen darstellt Rate, steuert die Schrittgröße der Gewichtsaktualisierung.
Stochastische Gradientenabstiegsmethode
Die stochastische Gradientenabstiegsmethode ist eine Variante der Gradientenabstiegsmethode. Ihre Grundidee besteht darin, jedes Mal zufällig eine Stichprobe auszuwählen, um den Gradienten zu berechnen und die Gewichte zu aktualisieren. Im Vergleich zur Gradientenabstiegsmethode kann die stochastische Gradientenabstiegsmethode bei der Verarbeitung großer Datensätze schneller konvergieren und effizienter sein. Konkret sind die Schritte der stochastischen Gradientenabstiegsmethode wie folgt:
Zuerst müssen wir die Trainingsdaten mischen und zufällig eine Stichprobe x_k auswählen, um den Gradienten zu berechnen. Dann können wir die Ableitung der Verlustfunktion in Bezug auf das Gewicht mit der folgenden Formel berechnen:
frac{partial MSE}{partial w_{ij}}=2(y_k-hat{y_k})cdot f' (sum_{j= 1}^{m}w_{ij}x_{kj})cdot x_{ki}
wobei y_k den wahren Wert der k-ten Stichprobe darstellt und hat{y_k} den Vorhersage der k-ten Stichprobe durch den Wert des neuronalen Netzwerks.
Schließlich können wir die Gewichte durch die folgende Formel aktualisieren:
w_{ij}=w_{ij}-alphacdotfrac{partial MSE}{partial w_{ij}}
wobei Alpha darstellt Lernrate, steuert die Schrittgröße der Gewichtsaktualisierung.
Batch-Gradientenabstiegsmethode
Die Batch-Gradientenabstiegsmethode ist eine weitere Variante der Gradientenabstiegsmethode. Ihre Grundidee besteht darin, jedes Mal eine kleine Menge Proben zu verwenden, um den Gradienten zu berechnen und die Gewichte zu aktualisieren. Im Vergleich zur Gradientenabstiegsmethode und der stochastischen Gradientenabstiegsmethode kann die Batch-Gradientenabstiegsmethode stabiler konvergieren und ist bei der Verarbeitung kleiner Datensätze effizienter. Konkret sind die Schritte der Batch-Gradienten-Abstiegsmethode wie folgt:
Zuerst müssen wir die Trainingsdaten in mehrere Mini-Batches gleicher Größe aufteilen, wobei jeder Mini-Batch b Proben enthält. Wir können dann den durchschnittlichen Gradienten der Verlustfunktion gegenüber den Gewichten auf jedem Mini-Batch berechnen, der lautet:
frac{1}{b}sum_{k=1}^{b}frac{partial MSE}{ partiell w_ {ij}}
wobei b die Mini-Batch-Größe darstellt. Schließlich können wir die Gewichte mit der folgenden Formel aktualisieren:
w_{ij}=w_{ij}-alphacdotfrac{1}{b}sum_{k=1}^{b}frac{partial MSE}{partial w_ {ij}}
Dabei stellt Alpha die Lernrate dar, die die Schrittgröße der Gewichtsaktualisierung steuert.
Das obige ist der detaillierte Inhalt vonTheorie und Techniken der Gewichtsaktualisierung in neuronalen Netzen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1658
1658
 14
14
 1415
1415
 52
52
 1309
1309
 25
25
 1257
1257
 29
29
 1231
1231
 24
24
 Eine Fallstudie zur Verwendung des bidirektionalen LSTM-Modells zur Textklassifizierung
Jan 24, 2024 am 10:36 AM
Eine Fallstudie zur Verwendung des bidirektionalen LSTM-Modells zur Textklassifizierung
Jan 24, 2024 am 10:36 AM
Das bidirektionale LSTM-Modell ist ein neuronales Netzwerk, das zur Textklassifizierung verwendet wird. Unten finden Sie ein einfaches Beispiel, das zeigt, wie bidirektionales LSTM für Textklassifizierungsaufgaben verwendet wird. Zuerst müssen wir die erforderlichen Bibliotheken und Module importieren: importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 Berechnung von Gleitkommaoperanden (FLOPS) für neuronale Netze
Jan 22, 2024 pm 07:21 PM
Berechnung von Gleitkommaoperanden (FLOPS) für neuronale Netze
Jan 22, 2024 pm 07:21 PM
FLOPS ist einer der Standards zur Bewertung der Computerleistung und dient zur Messung der Anzahl der Gleitkommaoperationen pro Sekunde. In neuronalen Netzen wird FLOPS häufig verwendet, um die Rechenkomplexität des Modells und die Nutzung von Rechenressourcen zu bewerten. Es ist ein wichtiger Indikator zur Messung der Rechenleistung und Effizienz eines Computers. Ein neuronales Netzwerk ist ein komplexes Modell, das aus mehreren Neuronenschichten besteht und für Aufgaben wie Datenklassifizierung, Regression und Clustering verwendet wird. Das Training und die Inferenz neuronaler Netze erfordert eine große Anzahl von Matrixmultiplikationen, Faltungen und anderen Rechenoperationen, sodass die Rechenkomplexität sehr hoch ist. Mit FLOPS (FloatingPointOperationsperSecond) kann die Rechenkomplexität neuronaler Netze gemessen werden, um die Effizienz der Rechenressourcennutzung des Modells zu bewerten. FLOP
 Entdecken Sie die Konzepte, Unterschiede, Vor- und Nachteile von RNN, LSTM und GRU
Jan 22, 2024 pm 07:51 PM
Entdecken Sie die Konzepte, Unterschiede, Vor- und Nachteile von RNN, LSTM und GRU
Jan 22, 2024 pm 07:51 PM
In Zeitreihendaten gibt es Abhängigkeiten zwischen Beobachtungen, sie sind also nicht unabhängig voneinander. Herkömmliche neuronale Netze behandeln jedoch jede Beobachtung als unabhängig, was die Fähigkeit des Modells zur Modellierung von Zeitreihendaten einschränkt. Um dieses Problem zu lösen, wurde das Recurrent Neural Network (RNN) eingeführt, das das Konzept des Speichers einführte, um die dynamischen Eigenschaften von Zeitreihendaten zu erfassen, indem Abhängigkeiten zwischen Datenpunkten im Netzwerk hergestellt werden. Durch wiederkehrende Verbindungen kann RNN frühere Informationen an die aktuelle Beobachtung weitergeben, um zukünftige Werte besser vorherzusagen. Dies macht RNN zu einem leistungsstarken Werkzeug für Aufgaben mit Zeitreihendaten. Aber wie erreicht RNN diese Art von Gedächtnis? RNN realisiert das Gedächtnis durch die Rückkopplungsschleife im neuronalen Netzwerk. Dies ist der Unterschied zwischen RNN und herkömmlichen neuronalen Netzwerken.
 Einführung in SqueezeNet und seine Eigenschaften
Jan 22, 2024 pm 07:15 PM
Einführung in SqueezeNet und seine Eigenschaften
Jan 22, 2024 pm 07:15 PM
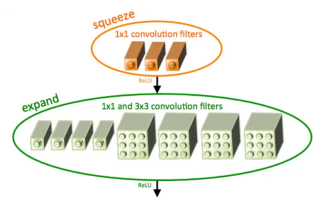
SqueezeNet ist ein kleiner und präziser Algorithmus, der eine gute Balance zwischen hoher Genauigkeit und geringer Komplexität schafft und sich daher ideal für mobile und eingebettete Systeme mit begrenzten Ressourcen eignet. Im Jahr 2016 schlugen Forscher von DeepScale, der University of California, Berkeley und der Stanford University SqueezeNet vor, ein kompaktes und effizientes Faltungs-Neuronales Netzwerk (CNN). In den letzten Jahren haben Forscher mehrere Verbesserungen an SqueezeNet vorgenommen, darunter SqueezeNetv1.1 und SqueezeNetv2.0. Verbesserungen in beiden Versionen erhöhen nicht nur die Genauigkeit, sondern senken auch die Rechenkosten. Genauigkeit von SqueezeNetv1.1 im ImageNet-Datensatz
 Vergleichen Sie die Ähnlichkeiten, Unterschiede und Beziehungen zwischen erweiterter Faltung und atröser Faltung
Jan 22, 2024 pm 10:27 PM
Vergleichen Sie die Ähnlichkeiten, Unterschiede und Beziehungen zwischen erweiterter Faltung und atröser Faltung
Jan 22, 2024 pm 10:27 PM
Dilatierte Faltung und erweiterte Faltung sind häufig verwendete Operationen in Faltungs-Neuronalen Netzen. In diesem Artikel werden ihre Unterschiede und Beziehungen im Detail vorgestellt. 1. Erweiterte Faltung Die erweiterte Faltung, auch als erweiterte Faltung oder erweiterte Faltung bekannt, ist eine Operation in einem Faltungs-Neuronalen Netzwerk. Es handelt sich um eine Erweiterung, die auf der herkömmlichen Faltungsoperation basiert und das Empfangsfeld des Faltungskerns durch Einfügen von Löchern in den Faltungskern erhöht. Auf diese Weise kann das Netzwerk ein breiteres Spektrum an Funktionen besser erfassen. Die erweiterte Faltung wird im Bereich der Bildverarbeitung häufig verwendet und kann die Leistung des Netzwerks verbessern, ohne die Anzahl der Parameter und den Rechenaufwand zu erhöhen. Durch die Erweiterung des Empfangsfelds des Faltungskerns kann die erweiterte Faltung die globalen Informationen im Bild besser verarbeiten und dadurch den Effekt der Merkmalsextraktion verbessern. Die Hauptidee der erweiterten Faltung besteht darin, einige einzuführen
 Twin Neural Network: Prinzip- und Anwendungsanalyse
Jan 24, 2024 pm 04:18 PM
Twin Neural Network: Prinzip- und Anwendungsanalyse
Jan 24, 2024 pm 04:18 PM
Das Siamese Neural Network ist eine einzigartige künstliche neuronale Netzwerkstruktur. Es besteht aus zwei identischen neuronalen Netzen mit denselben Parametern und Gewichten. Gleichzeitig teilen die beiden Netzwerke auch die gleichen Eingabedaten. Dieses Design wurde von Zwillingen inspiriert, da die beiden neuronalen Netze strukturell identisch sind. Das Prinzip des siamesischen neuronalen Netzwerks besteht darin, bestimmte Aufgaben wie Bildabgleich, Textabgleich und Gesichtserkennung durch den Vergleich der Ähnlichkeit oder des Abstands zwischen zwei Eingabedaten auszuführen. Während des Trainings versucht das Netzwerk, ähnliche Daten benachbarten Regionen und unterschiedliche Daten entfernten Regionen zuzuordnen. Auf diese Weise kann das Netzwerk lernen, verschiedene Daten zu klassifizieren oder abzugleichen, um entsprechende Ergebnisse zu erzielen
 Kausales Faltungs-Neuronales Netzwerk
Jan 24, 2024 pm 12:42 PM
Kausales Faltungs-Neuronales Netzwerk
Jan 24, 2024 pm 12:42 PM
Das kausale Faltungs-Neuronale Netzwerk ist ein spezielles Faltungs-Neuronales Netzwerk, das für Kausalitätsprobleme in Zeitreihendaten entwickelt wurde. Im Vergleich zu herkömmlichen Faltungs-Neuronalen Netzen bieten kausale Faltungs-Neuronale Netze einzigartige Vorteile bei der Beibehaltung der kausalen Beziehung von Zeitreihen und werden häufig bei der Vorhersage und Analyse von Zeitreihendaten verwendet. Die Kernidee des kausalen Faltungs-Neuronalen Netzwerks besteht darin, Kausalität in die Faltungsoperation einzuführen. Herkömmliche Faltungs-Neuronale Netze können gleichzeitig Daten vor und nach dem aktuellen Zeitpunkt wahrnehmen, bei der Vorhersage von Zeitreihen kann dies jedoch zu Informationsverlustproblemen führen. Da die Vorhersageergebnisse zum aktuellen Zeitpunkt durch die Daten zu zukünftigen Zeitpunkten beeinflusst werden. Das kausale Faltungs-Neuronale Netzwerk löst dieses Problem. Es kann nur den aktuellen Zeitpunkt und frühere Daten wahrnehmen, aber keine zukünftigen Daten.
 Bildrauschen mithilfe von Faltungs-Neuronalen Netzen
Jan 23, 2024 pm 11:48 PM
Bildrauschen mithilfe von Faltungs-Neuronalen Netzen
Jan 23, 2024 pm 11:48 PM
Faltungs-Neuronale Netze eignen sich gut für Aufgaben zur Bildrauschunterdrückung. Es nutzt die erlernten Filter, um das Rauschen zu filtern und so das Originalbild wiederherzustellen. In diesem Artikel wird die Methode zur Bildentrauschung basierend auf einem Faltungs-Neuronalen Netzwerk ausführlich vorgestellt. 1. Überblick über das Convolutional Neural Network Das Convolutional Neural Network ist ein Deep-Learning-Algorithmus, der eine Kombination aus mehreren Faltungsschichten, Pooling-Schichten und vollständig verbundenen Schichten verwendet, um Bildmerkmale zu lernen und zu klassifizieren. In der Faltungsschicht werden die lokalen Merkmale des Bildes durch Faltungsoperationen extrahiert und so die räumliche Korrelation im Bild erfasst. Die Pooling-Schicht reduziert den Rechenaufwand durch Reduzierung der Feature-Dimension und behält die Hauptfeatures bei. Die vollständig verbundene Schicht ist für die Zuordnung erlernter Merkmale und Beschriftungen zur Implementierung der Bildklassifizierung oder anderer Aufgaben verantwortlich. Das Design dieser Netzwerkstruktur macht das Faltungs-Neuronale Netzwerk für die Bildverarbeitung und -erkennung nützlich.



