 Backend-Entwicklung
Backend-Entwicklung
 Python-Tutorial
Python-Tutorial
 Analysieren Sie den Ford-Fulkerson-Algorithmus und implementieren Sie ihn über Python
Analysieren Sie den Ford-Fulkerson-Algorithmus und implementieren Sie ihn über Python
Analysieren Sie den Ford-Fulkerson-Algorithmus und implementieren Sie ihn über Python
Der Ford-Fulkerson-Algorithmus ist ein gieriger Algorithmus, der zur Berechnung des maximalen Datenverkehrs im Netzwerk verwendet wird. Das Prinzip besteht darin, einen Erweiterungspfad mit einer positiven Restkapazität zu finden. Solange der Erweiterungspfad gefunden wird, können Sie weiterhin Pfade hinzufügen und den Verkehr berechnen. Bis der Verstärkungspfad nicht mehr vorhanden ist, kann die maximale Durchflussrate erreicht werden.
Terminologie des Ford-Fulkerson-Algorithmus
Restkapazität: Es handelt sich um die Kapazität abzüglich des Durchflusses. Im Ford-Fulkerson-Algorithmus ist die verbleibende Kapazität eine positive Zahl, bevor sie weiterhin ein Pfad sein kann.
Restnetzwerk: Es handelt sich um ein Netzwerk mit denselben Scheitelpunkten und Kanten, das die Restkapazität als Kapazität verwendet.
Erweiterter Pfad: Dies ist der Pfad vom Quellpunkt zum Empfangspunkt im Restdiagramm mit einer Endkapazität von 0.
Beispiel für das Prinzip des Ford-Fulkerson-Algorithmus
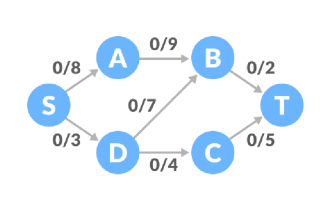
Das Konzept ist möglicherweise nicht sehr klar. Schauen wir uns ein Beispiel an. Der anfängliche Verkehr an allen Kanten des Flussnetzwerks ist 0, und es gibt eine entsprechende obere Kapazitätsgrenze sei S und der Empfangspunkt sei T. .
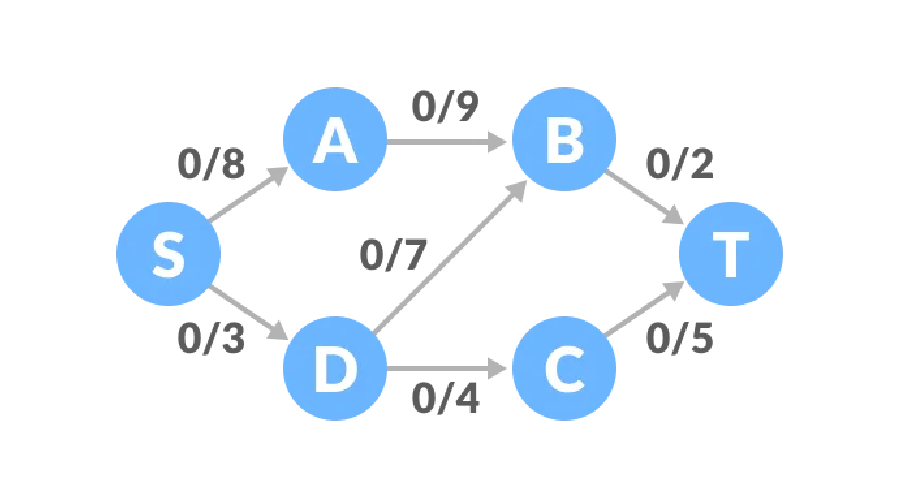
Pfad eins, die verbleibende Kapazität des S-A-B-T-Pfads beträgt 8, 9, 2 und der Mindestwert beträgt 2, sodass der Verkehr von Pfad eins 2 und der Verkehr des Netzwerkdiagramms 2 beträgt.
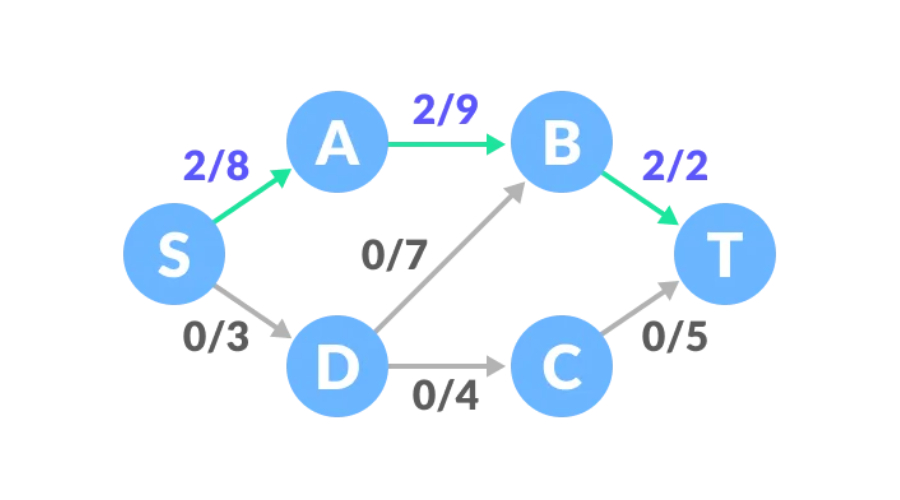
Pfad zwei, die verbleibende Kapazität des S-D-C-T-Pfads beträgt 3, 4, 5 und der Mindestwert beträgt 3, sodass wir den Datenverkehr um 3 erhöhen können und der Netzwerkverkehr 5 beträgt.
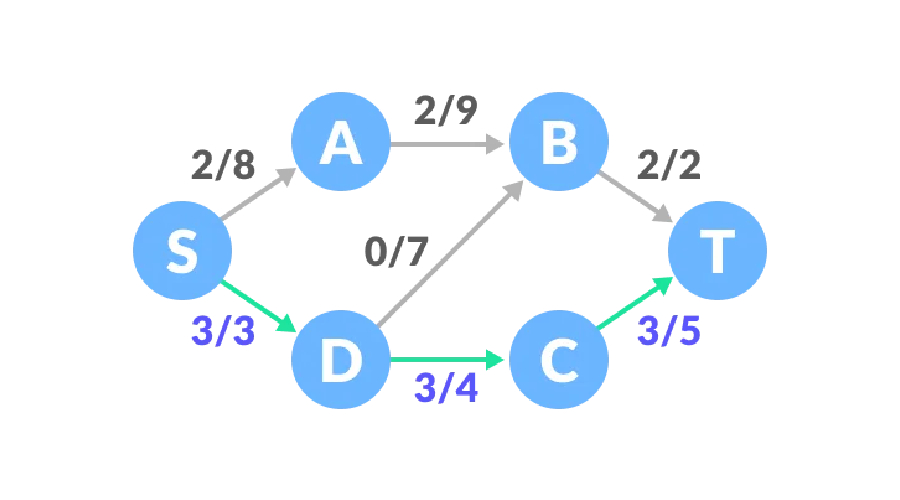
Pfad drei, die verbleibende Kapazität des S-A-B-D-C-T-Pfads beträgt 6, 7, 7, 1, 2 und der Mindestwert ist 1, sodass der Datenverkehr um 1 steigt und der Netzwerkverkehr 6 beträgt.
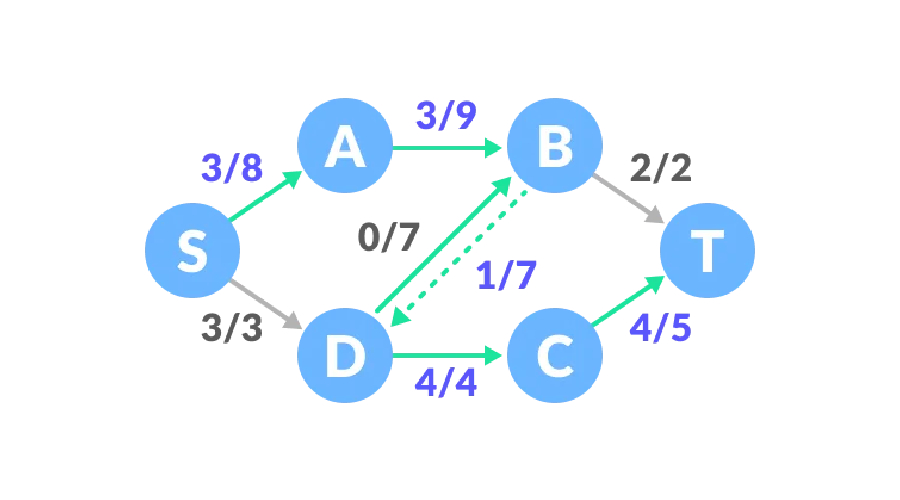
Zu diesem Zeitpunkt gibt es keine positive Restkapazität und der maximale Durchfluss dieses Durchflussnetzwerks beträgt 6.
Python implementiert den Ford-Fulkerson-Algorithmus
from collections import defaultdict
class Graph:
def __init__(self, graph):
self.graph = graph
self. ROW = len(graph)
def searching_algo_BFS(self, s, t, parent):
visited = [False] * (self.ROW)
queue = []
queue.append(s)
visited[s] = True
while queue:
u = queue.pop(0)
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
queue.append(ind)
visited[ind] = True
parent[ind] = u
return True if visited[t] else False
def ford_fulkerson(self, source, sink):
parent = [-1] * (self.ROW)
max_flow = 0
while self.searching_algo_BFS(source, sink, parent):
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min(path_flow, self.graph[parent[s]][s])
s = parent[s]
max_flow += path_flow
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
graph = [[0, 8, 0, 0, 3, 0],
[0, 0, 9, 0, 0, 0],
[0, 0, 0, 0, 7, 2],
[0, 0, 0, 0, 0, 5],
[0, 0, 7, 4, 0, 0],
[0, 0, 0, 0, 0, 0]]
g = Graph(graph)
source = 0
sink = 5
print("Max Flow: %d " % g.ford_fulkerson(source, sink))Das obige ist der detaillierte Inhalt vonAnalysieren Sie den Ford-Fulkerson-Algorithmus und implementieren Sie ihn über Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 So implementieren Sie einen Greedy-Algorithmus in C#
Sep 19, 2023 am 11:48 AM
So implementieren Sie einen Greedy-Algorithmus in C#
Sep 19, 2023 am 11:48 AM
So implementieren Sie den Greedy-Algorithmus in C# Der Greedy-Algorithmus (Greedy-Algorithmus) ist eine häufig verwendete Methode zur Problemlösung. Er wählt jedes Mal die aktuell optimale Lösung aus, in der Hoffnung, die globale optimale Lösung zu erhalten. In C# können wir Greedy-Algorithmen verwenden, um viele praktische Probleme zu lösen. In diesem Artikel wird die Implementierung des Greedy-Algorithmus in C# vorgestellt und spezifische Codebeispiele bereitgestellt. 1. Grundprinzipien des Greedy-Algorithmus Die Grundidee des Greedy-Algorithmus besteht darin, jedes Mal die aktuell optimale Lösung auszuwählen, unabhängig von den möglichen Auswirkungen nachfolgender Schritte. Diese Art des Denkens
 Wie implementiert man mithilfe eines Greedy-Algorithmus eine effiziente Lösung für das Problem des geringsten Münzwechsels in PHP?
Sep 19, 2023 am 10:22 AM
Wie implementiert man mithilfe eines Greedy-Algorithmus eine effiziente Lösung für das Problem des geringsten Münzwechsels in PHP?
Sep 19, 2023 am 10:22 AM
Wie implementiert man mithilfe des Greedy-Algorithmus eine effiziente Lösung für das Problem des geringsten Münzwechsels in PHP? Einleitung: Im täglichen Leben müssen wir oft Veränderungen vornehmen, insbesondere beim Einkaufen oder Handeln. Um möglichst wenig Münzen zu verbrauchen, sollte der Wechselbetrag mit möglichst wenigen Münzen zusammengefasst werden. In der Computerprogrammierung können wir einen gierigen Algorithmus verwenden, um dieses Problem zu lösen und eine effiziente Lösung zu erhalten. In diesem Artikel wird erläutert, wie Sie mit dem Greedy-Algorithmus in PHP eine effiziente Lösung für das Problem des minimalen Münzwechsels erreichen, und entsprechende Codebeispiele bereitstellen.
 Analysieren Sie den Ford-Fulkerson-Algorithmus und implementieren Sie ihn über Python
Jan 22, 2024 pm 08:09 PM
Analysieren Sie den Ford-Fulkerson-Algorithmus und implementieren Sie ihn über Python
Jan 22, 2024 pm 08:09 PM
Der Ford-Fulkerson-Algorithmus ist ein Greedy-Algorithmus zur Berechnung der maximalen Durchflussrate in einem Netzwerk. Das Prinzip besteht darin, einen Erweiterungspfad mit einer positiven Restkapazität zu finden. Solange der Erweiterungspfad gefunden wird, können Sie weiterhin Pfade hinzufügen und den Verkehr berechnen. Bis der Verstärkungspfad nicht mehr vorhanden ist, kann die maximale Durchflussrate erreicht werden. Der Begriff „Restkapazität“ des Ford-Fulkerson-Algorithmus besteht darin, den Fluss von der Kapazität zu subtrahieren. Beim Ford-Fulkerson-Algorithmus ist die verbleibende Kapazität eine positive Zahl, bevor sie weiterhin als Pfad verwendet werden kann. Restnetzwerk: Es handelt sich um ein Netzwerk mit denselben Scheitelpunkten und Kanten, das die Restkapazität als Kapazität verwendet. Erweiterter Pfad: Dies ist der Pfad vom Quellpunkt zum Empfangspunkt im Restdiagramm mit einer Endkapazität von 0. Ein möglicher Überblick über das Prinzip des Ford-Fulkerson-Algorithmus, Beispiel
 Wie implementiert man einen gierigen Algorithmus mit Python?
Sep 19, 2023 am 11:43 AM
Wie implementiert man einen gierigen Algorithmus mit Python?
Sep 19, 2023 am 11:43 AM
Wie implementiert man einen gierigen Algorithmus mit Python? Der Greedy-Algorithmus ist ein einfacher und effektiver Algorithmus, der sich zur Lösung von Problemen mit optimalen Unterstruktureigenschaften eignet. In jedem Auswahlschritt wird die aktuell beste Wahl getroffen, in der Hoffnung, die global optimale Lösung zu finden. In diesem Artikel stellen wir anhand spezifischer Codebeispiele vor, wie Python zum Implementieren des Greedy-Algorithmus verwendet wird. 1. Die Grundidee des Greedy-Algorithmus Die Grundidee des Greedy-Algorithmus besteht darin, in jedem Schritt die optimale Lösung im aktuellen Zustand auszuwählen und dann
 Wie schreibe ich einen Greedy-Algorithmus mit PHP
Jul 07, 2023 pm 03:45 PM
Wie schreibe ich einen Greedy-Algorithmus mit PHP
Jul 07, 2023 pm 03:45 PM
So schreiben Sie mit PHP einen Greedy-Algorithmus. Der Greedy-Algorithmus (Greedy-Algorithmus) ist ein einfacher und effektiver Algorithmus, der zur Lösung einer Art Optimierungsproblem verwendet wird. Die Grundidee besteht darin, bei jedem Schritt die Wahl zu treffen, die im Moment am besten erscheint, ohne Rücksicht auf zukünftige Konsequenzen. In diesem Artikel wird vorgestellt, wie man mit PHP einen Greedy-Algorithmus schreibt, und relevante Codebeispiele bereitgestellt. 1. Problembeschreibung Bevor wir den Greedy-Algorithmus erklären, definieren wir zum besseren Verständnis zunächst ein spezifisches Problem. Angenommen, es gibt eine Reihe von Aufgaben, jede Aufgabe hat einen Anfang
 Greedy-Algorithmus und seine Implementierung in C++
Aug 22, 2023 am 10:04 AM
Greedy-Algorithmus und seine Implementierung in C++
Aug 22, 2023 am 10:04 AM
Der Greedy-Algorithmus ist eine häufig verwendete Algorithmusidee und wird häufig bei vielen Problemen eingesetzt. Der Kerngedanke besteht darin, bei der Entscheidungsfindung in jedem Schritt nur die unmittelbar optimale Lösung zu berücksichtigen, ohne die langfristigen Auswirkungen zu berücksichtigen. In C++ umfasst die Implementierung gieriger Algorithmen häufig grundlegende Operationen wie Sortieren und Datenverarbeitung. Im Folgenden stellen wir die Idee des Greedy-Algorithmus und seine Implementierung in C++ für mehrere typische Probleme vor. 1. Aktivitätsplanungsproblem Bei einer Reihe von Aktivitäten hat jede Aktivität ihre Start- und Endzeit, und eine Person kann jeweils nur an einer Aktivität teilnehmen.
 So implementieren Sie einen gierigen Algorithmus mit Java
Sep 19, 2023 am 11:13 AM
So implementieren Sie einen gierigen Algorithmus mit Java
Sep 19, 2023 am 11:13 AM
So implementieren Sie einen gierigen Algorithmus mit Java. Der gierige Algorithmus (GreedyAlgorithm) ist eine algorithmische Idee zur Lösung von Problemen. Sein Merkmal besteht darin, bei jedem Schritt die aktuell optimale Lösung auszuwählen, in der Hoffnung, durch jede lokale optimale Lösung schließlich die globale optimale Lösung zu erreichen. Die einfachen und effizienten Eigenschaften des Greedy-Algorithmus machen ihn zu einem häufig verwendeten Algorithmus zur Lösung einiger Optimierungsprobleme oder bestimmter spezifischer Probleme. In diesem Artikel wird die Implementierung des Greedy-Algorithmus mit Java vorgestellt und spezifische Codebeispiele bereitgestellt. 1. Die Grundidee des Greedy-Algorithmus. Die Grundlage des Greedy-Algorithmus
 C/C++-Programm für einen gierigen Algorithmus zum Ermitteln der Mindestanzahl an Münzen
Sep 19, 2023 pm 11:01 PM
C/C++-Programm für einen gierigen Algorithmus zum Ermitteln der Mindestanzahl an Münzen
Sep 19, 2023 pm 11:01 PM
Der Greedy-Algorithmus ist ein Algorithmus, der verwendet wird, um die optimale Lösung für ein bestimmtes Problem zu finden. Der Greedy-Algorithmus funktioniert, indem er für jeden Teil eine lokal optimale Lösung findet (die optimale Lösung für einen Teil des Problems) und zeigt so, dass eine globale optimale Lösung gefunden werden kann. In diesem Problem verwenden wir den Greedy-Algorithmus, um die Mindestanzahl an Münzen/Banknoten zu ermitteln, aus denen eine bestimmte Summe bestehen kann. Dabei berücksichtigen wir alle gültigen Münzen oder Banknoten, also die Nennwerte {1,2,5,10,20,50,100,200,500,2000}. Wir müssen die Anzahl Münzen/Banknoten zurückgeben, die für die Summe erforderlich sind. Lassen Sie uns einige Beispiele geben, um den Kontext besser zu verstehen – Beispiel 1 – Eingabe: 1231 Ausgabe: 7 Beschreibung – Wir benötigen zwei 500-Rupien-Scheine



