
Der k-Nearest-Neighbor-Algorithmus ist ein instanzbasierter oder speicherbasierter Algorithmus für maschinelles Lernen zur Klassifizierung und Erkennung. Sein Prinzip besteht darin, zu klassifizieren, indem die Daten des nächsten Nachbarn eines bestimmten Abfragepunkts ermittelt werden. Da der Algorithmus stark auf gespeicherten Trainingsdaten basiert, kann er als nichtparametrische Lernmethode betrachtet werden. Der
k-Nächste-Nachbarn-Algorithmus eignet sich zur Behandlung von Klassifizierungs- oder Regressionsproblemen. Bei Klassifizierungsproblemen arbeitet es mit diskreten Werten, während es bei Regressionsproblemen mit kontinuierlichen Werten arbeitet. Vor der Klassifizierung muss die Entfernung definiert werden, und es gibt viele Möglichkeiten für gängige Entfernungsmaße.
Dies ist ein häufig verwendetes Abstandsmaß und funktioniert für Vektoren mit reellen Werten. Die Formel misst den Luftlinienabstand zwischen einem Abfragepunkt und einem anderen Punkt.
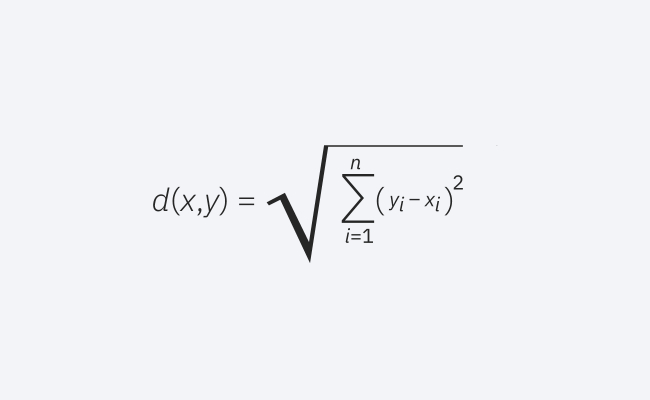
Euklidische Distanzformel
Dies ist auch ein beliebtes Distanzmaß, das den absoluten Wert zwischen zwei Punkten misst.

Manhattan-Distanzformel
Dieses Distanzmaß ist eine verallgemeinerte Form der euklidischen und Manhattan-Distanzmaße.

Minkowski-Distanzformel
Diese Technik wird oft mit booleschen oder String-Vektoren verwendet, um Punkte zu identifizieren, bei denen die Vektoren nicht übereinstimmen. Daher wird es auch Überlappungsmaß genannt.

Hamming-Abstandsformel
Um zu bestimmen, welche Datenpunkte einem bestimmten Abfragepunkt am nächsten liegen, muss der Abstand zwischen dem Abfragepunkt und anderen Datenpunkten berechnet werden. Diese Distanzmaße helfen bei der Bildung von Entscheidungsgrenzen, die Abfragepunkte in verschiedene Regionen unterteilen.
Das obige ist der detaillierte Inhalt vonAnwendung häufig verwendeter Entfernungsmessmethoden im K-Nearest-Neighbor-Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 So ändern Sie den Dateityp in Win7
So ändern Sie den Dateityp in Win7
 Einführung in die Bedeutung eines ungültigen Passworts
Einführung in die Bedeutung eines ungültigen Passworts
 So laden Sie HTML hoch
So laden Sie HTML hoch
 So eröffnen Sie ein Konto bei U-Währung
So eröffnen Sie ein Konto bei U-Währung
 So öffnen Sie eine OFD-Datei
So öffnen Sie eine OFD-Datei
 So extrahieren Sie Audio aus Video in Java
So extrahieren Sie Audio aus Video in Java
 jsonp löst domänenübergreifende Probleme
jsonp löst domänenübergreifende Probleme
 Was bedeutet c#?
Was bedeutet c#?
 Kosteneffizienzanalyse des Lernens von Python, Java und C++
Kosteneffizienzanalyse des Lernens von Python, Java und C++




