Verständnis der ReLU-Funktion beim maschinellen Lernen

Was ist die ReLU-Funktion?

Die ReLU-Funktion ist eine mathematische Funktion, die als f(x)=max(0,x) definiert ist, wobei x eine beliebige reelle Zahl ist. Einfach ausgedrückt: Wenn x kleiner oder gleich 0 ist, gibt die Funktion 0 zurück. Andernfalls gib x zurück.

Kontinuität und Differenzierbarkeit der ReLU-Funktion

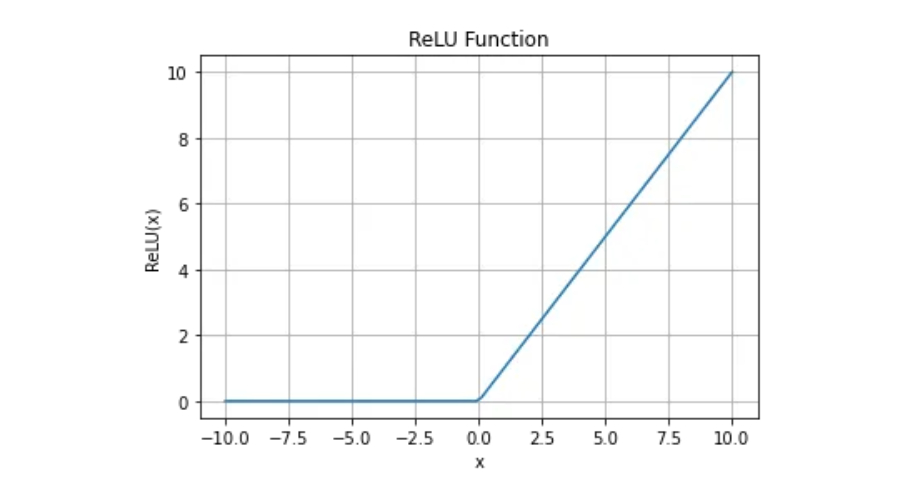
Für eine differenzierbare Funktion muss sie zunächst stetig sein. Die ReLU-Funktion erfüllt die Kontinuitätsanforderung, aber die Ableitung bei x=0 existiert nicht, sodass die ReLU-Funktion zu diesem Zeitpunkt nicht differenzierbar ist.

Warum wird die ReLU-Funktion immer noch beim Deep Learning verwendet?

Obwohl die ReLU-Funktion bei x=0 nicht differenzierbar ist, können wir sie dennoch beim Deep Learning anwenden, indem wir den Optimierungsalgorithmus optimieren. Der Gradientenabstieg ist ein Optimierungsalgorithmus zur Minimierung einer Kostenfunktion. Wenn die ReLU-Funktion bei x=0 keine definierte Ableitung hat, können wir sie auf 0 oder einen anderen Wert setzen und den Optimierungsprozess fortsetzen. Auf diese Weise können wir die nichtlinearen Eigenschaften der ReLU-Funktion nutzen, um die Leistung des Deep-Learning-Modells zu verbessern.

Generell ist die ReLU-Aktivierungsfunktion eine der beliebtesten Aktivierungsfunktionen in Deep-Learning-Netzwerken. Seine Einfachheit und hohe Recheneffizienz machen es zu einem wichtigen Werkzeug zur Verbesserung der Konvergenz während des Trainings. Obwohl es bei x=0 nicht differenzierbar ist, hat dies keinen Einfluss auf seine Anwendung beim Gradientenabstieg. Daher ist die ReLU-Funktion ein vielseitiges und leistungsstarkes Werkzeug im Bereich des maschinellen Lernens.

Vorteile der ReLU-Funktion

1.

Die Gleichrichterfunktion ist sehr einfach zu implementieren und erfordert eine max()-Funktion.

2. Repräsentationssparsität

Sparse Repräsentation ist eine wünschenswerte Eigenschaft beim Repräsentationslernen, da sie das Lernen beschleunigt und Modelle vereinfacht. Dadurch kann die Aktivierung der verborgenen Schicht des neuronalen Netzwerks einen oder mehrere echte Nullwerte enthalten, was bedeutet, dass negative Eingaben auch echte Nullwerte ausgeben können. Diese Fähigkeit ermöglicht es neuronalen Netzen, große Datenmengen besser zu verarbeiten und kann den Bedarf an Rechen- und Speicherressourcen reduzieren. Daher ist eine spärliche Darstellung sehr wichtig, um die Leistung und Effizienz neuronaler Netze zu optimieren.

3. Lineares Verhalten

Die Gleichrichterfunktion sieht aus und verhält sich ähnlich wie die lineare Aktivierungsfunktion. Geeignet zur Optimierung von linearem oder nahezu linearem Verhalten.

Das obige ist der detaillierte Inhalt vonVerständnis der ReLU-Funktion beim maschinellen Lernen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!